浅海观测网的系泊系统的设计

高立刚，许友军，刘若男，李 伟

(南华大学数理学院，湖南衡阳，421001)

系泊系统设计的本质就是使得浮标吃水深度、钢桶倾斜角度尽可能的小，游动区域尽可能窄［1－2］。在选定指定的电焊锚链，以及传输节点分布在水深、海水密度都已知的海域，针对海面风速v对应下的系泊系统(如图1)状态，文中分别研究锚链存在部分沉底时的风速12m/s，锚链刚好不沉底时的风速24m/s，锚链被拉动时的风速36m/s下各自情况下的系泊系统具体状态，从而得出相对应速度区间下满足的悬链数学公式模型。

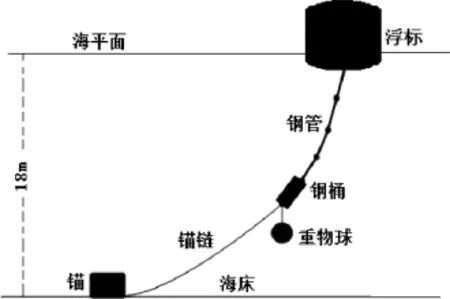
图1 系泊系统示意图Fig.1 Mooring system schematic diagram

1 临界风速模型

根据悬链线模型［1－8］，考虑锚链沉底情况，假设理想状态下(即刚好不沉底)，锚链长度为22.05m(此处锚链长度是根据图1中水深18m算出来的)，并且改变风速时，重物球与钢桶的高度改变很小，这里假定高度不变;再对得到的一系列的不同风速下的锚链方程，并利用Matlab绘制出一系列风速下的高度变化(见图2)，取同一高度下的锚链长度，找出一系列风速下的弧长等于22.05m时的风速V0，即为保证锚链恰好不沉底的风速。

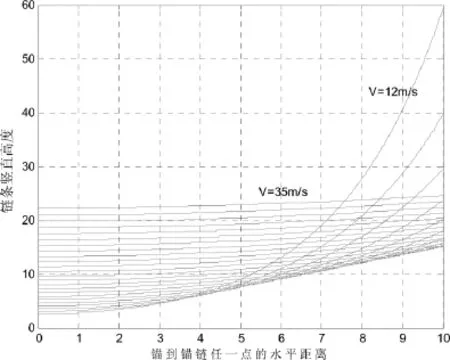
图2 不同风速下的锚链满足的悬链线Fig.2 The anchors under different wind speeds meet the catenary lines

考虑其钢管、浮标、重物等物体的浮力，结合一系列的不同风速下的锚链方程，满足弧长s=22.05m、h=12.306m时的风速V0=23.5m/s，即:

(1)当V＜V0时，锚链的底端是存在部分长度的沉底，即θ=0°(等于0)，此时系泊系统的状态可以仿照12m/s风速时求出相对应的系泊状态;

(2)当V=V0时，锚链的底端与锚点恰好与海床保持水平，即θ=0°;

(3)当V＞V0时，锚链在锚点与海床的夹角θ＞0°，此时系泊系统的状态可以仿照24m/s风速时求出相对应的系泊状态。

当海面风速V=12m/s时，锚链只有没有接触海床的部分满足悬链线方程的条件，故而，考虑未沉底部分锚链:

根据锚链竖直高度Δh=12.306 m，利用弧长公式得到未沉底的锚链的长度Lx=15.3548m，从而得知当V=12m/s时，沉底的锚链长x'=6.6952m。

根据弧长［2］可得到锚链方程上每点的斜率满足:

其中σ为链条单位长度的质量，H为锚链水平向左的张力，g为重力加速度，x为锚链水平长度。

当x=7.5567m，锚链与钢桶接触点的斜率为y'=4.4808，此时锚链在钢桶节点处与竖直方向的夹角为θ=12.5415°。

对上述过程进行多次迭代，得到当V=12m/s时，沉底的锚链长x'=6.6573m。当x'=6.6573m时，锚链在钢桶节点处与竖直方向的夹角θ=12.6231°。

由上述讨论，根据沉底锚链长以及未沉底锚链的曲线方程，到V=12m/s时锚链在水中的形状，如图3所示。

同理，考虑到V=24m/s时，锚链不存在沉底，故根据锚链方程得到V=24m/s时锚链在水中的形状，如图4所示。

图3 12m/s时锚链整体形状图Fig.3 The overall shape of the chain at 12m/s

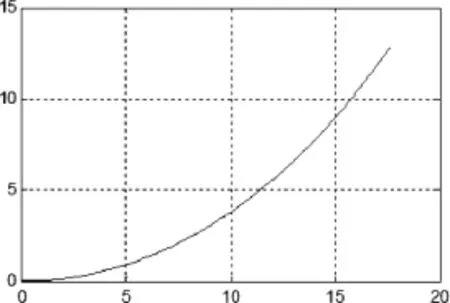
图4 24m/s时锚链整体形状Fig.4 The overall shape of the chain at 24m/s

(注:针对12m/s，以锚为坐标原点，0＜x＜6.6573m时锚链沉底，即竖直高度 y=0m;6.6573m≤x＜14.2609m时，锚链形状满足悬链线方程)

2 力系平衡模型

取出钢桶作为隔离体，并对其进行受力分析［4］，如图5所示。

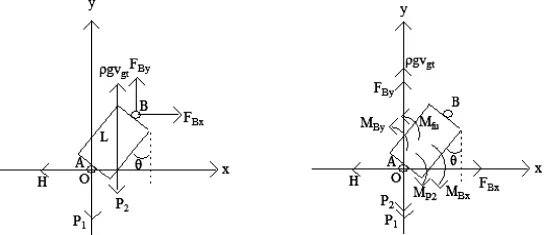
图5 钢桶平移力系后产生弯矩分析Fig.5 Analysis of bending moment after translation of steel drum

FBy、FBx为1号钢管BC施加给钢桶的作用力，P2为钢管自身重力，P1为重物球、重物球的浮力和锚链的重力之和，因此有

其中mm为不在海底的那部分锚链的质量，mz为重物球质量，g为重力加速度，Fm为锚链受到的浮力，Fz为重物球受到的浮力。

根据力的平移定理［5］，可以求出力平移后产生的弯矩。同时根据平衡力系平衡条件可得:

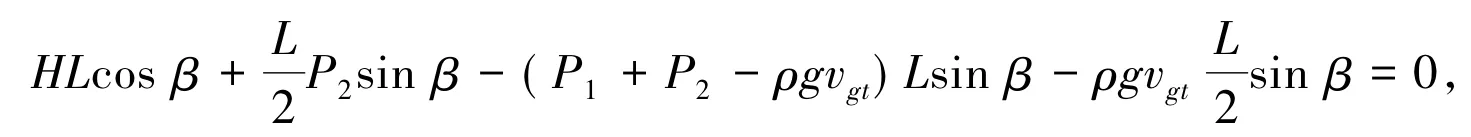
解得钢桶的倾斜角β为

其中ρ为海水密度，vgt为钢桶体积。

由风荷载近似公式F=0.625×sv2，

(1)当v=12m/s，F=237.24N=H，锚链在钢桶节点处与竖直方向的夹角为θ=12.6231 °，吃水深度 y=0.682 时，可得可得钢桶的倾斜角β=1.078698141°。

(2)当风速为v=24m/s，吃水深度为y=0.7010m，锚链在钢桶节点处与竖直方向的夹角为 θ=31.7177°，可得可得钢桶的倾斜角β=3.875574314°。

同理可得钢管角度求解公式:

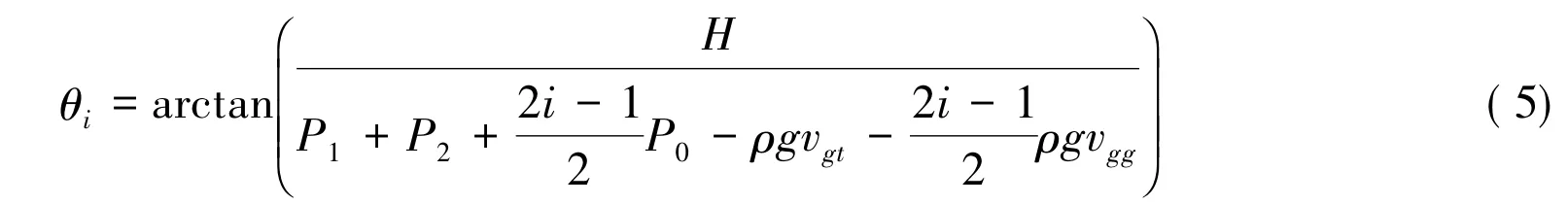
其中θi为第i根钢管的倾斜角，L1为钢管长度。

3 游动区域的求解模型

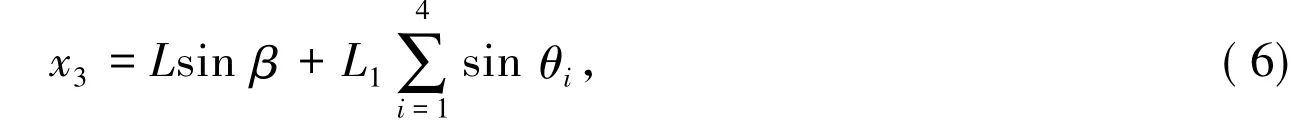
(1)当风速为12m/s时，x3≈0.0905m游动半径为:r=x3+14.2519=14.3424m;

(2)当风速为24m/s时，x3≈0.3322m游动半径为:r=x3+17.1581m=17.4903m。

根据临界风速模型、力系平衡模型、游动区域的求解模型，针对水深18m的水域状况，计算得出不同风速(12m/s与24m/s)下系泊系统各部分的角度改变参数，如表1。

由上可得钢桶及钢管在海底的投影长度x3，即

表1 具体风速下的系泊系统状态Table 1 The state of mooring system under specific wind speed

4 悬链重物的确定［6］

考虑到锚与锚链上端为整个悬链线的一部分，依据根据Δh=12.306m以及Lx=22.05m，据此得到锚的坐标点为(10.4286，30.8413)，得到:x=28.4563m，此时锚链在锚点与海床的夹角θ'=19.0149°;同理求出此时系泊系统的状态。

当v=36m/s时，角度及游动半径都是在固定锚时计算出来的，实际上锚链已经被拖动。此时，需要调节重物球的质量，使得钢桶的倾斜角度不超过5度，锚链在锚点与海床的夹角不超过16度。

利用改变步长反复迭代来对相应的角度进行考虑，发现将重物球质量增加到3200kg满足条件，此时浮标吃水深度由h=0.723m变为h=1.3444m，同时考虑到钢桶在36m/s的情况下的倾斜角θ=8.5589°以及钢管的倾斜角，综合得到Δh=12.3736m，相应的锚链方程改变为

当海面风速V=36m/s时，易知锚链底端不存在沉底的情况，得到对应的锚链方程:

经过多次回代运算，使得浮标吃水高度不断接近精确值，得到浮标吃水深度由h=0.723m变为h=1.2156m，此时锚链与海床的夹角θ'=6.3405°＜16°，钢桶的倾斜角为β=4.7121°＜5°，增加的重物质量为 2000kg。

针对市场上锚链的不同型号(见表2)，这里对型号的选择进行讨论。

表2 锚链型号和参数表Table 2 Chain model and parameter table

这里对于锚链型号的确定，文中考虑等水平力作用下的不同型号下的锚链方程，并对同一高度下的锚链的重量进行比较，取等水平力作用下同一高度锚链的重量作为参考量，取五种型号中的重量最少的锚链。

对于Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ型号的单位长度，并对于给定同一水平作用力1000N时，满足:

以及不同型号下的锚链在等水平力的作用下，锚链的竖直高度的改变如图6所示。

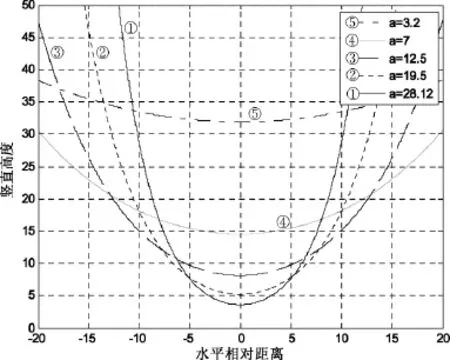
图6 不同型号等水平力下的悬链曲线图Fig.6 The catenary curve of the horizontal force of different models

对于给定的相对锚同一高度值12m，计算出不同型号下的弧线长

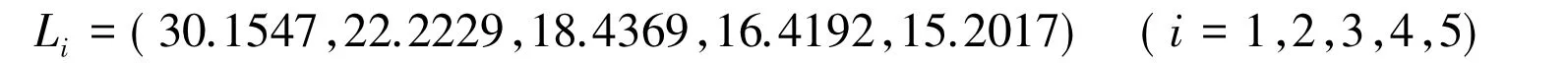
对应的重量为

Mi=(96.4950，155.5603，230.46125，320.1744，427.4718)，

由于近海水深介于16m～20m之间，布放区域海水的最大速度为1.5m/s，风速最大达到36m/s，这里考虑最恶劣的情况下，即水深为20m，海水速度为1.5m/s，风速36m/s下的系泊系统的设计［7］，倘若最恶劣的条件下都满足要求的系泊系统，在其他情况下系泊系统也满足要求。

当水深为20m，海水速度为1.5m/s，风速36m/s时，通过多次对重物球重量的调整得到满足条件下的悬链线方程:

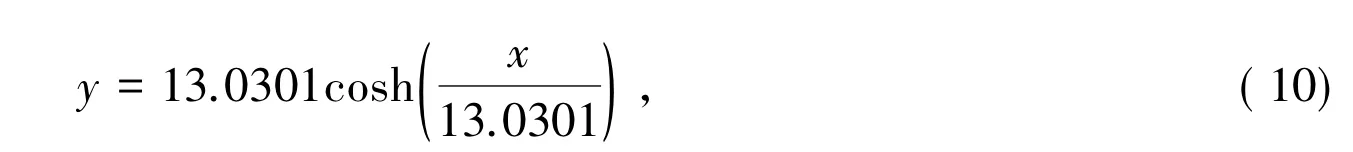
此时，钢桶的倾斜角β=4.7317°＜5°，说明该悬链线方程下的系泊系统满足最恶劣的情况。该系泊系统的锚链的长度s=23.0299m，重物球质量m=3500kg。此时，系泊系统各部分的角度改变参数见表3。

表3 36m/s风速下的系泊系统状态Table 3 Mooring system state at 36m/s

5 模型的推广与改进

这里研究了近浅海观测网的系泊系统的设计问题，在系泊系统的设计方面有一定的参考价值。对于其中的不足，可以在参考水流层流情况下对系泊系统进行具体研究，以得到更为准确解，或从多角度对锚链进行参考分析，以选择最优锚链型号。再可利用软件对所得数值解进行验证。

参考文献:

［1］柳燕.从达·芬奇的问题到一条著名的曲线——悬链线［J］.科技信息，2012，1:135－136.

［2］胡灵斌，唐军.悬链线方程的求解及其应用［J］.船舶，2004，1:17－20.

［3］杨万昌，沈潘浩.多成分悬链式锚泊线静态特性分析［J］.中国水运，2016，37(03):36－37.

［4］王铎，程靳.理论力学［M］.(第 7 版).北京:高等教育出版社，2009.

［5］邢富冲.悬链线弛垂度的计算方法［J］.数学的实践与认识，2004，34(11):98－101.

［6］李淑一，王树青.基于多体分析的浅水FPSO和水下软钢臂系泊系统运动特性研究［J］.中国海洋大学学报，2011，41(09):95－102.

［7］常洪波.倾斜海底及瞬态潮汐流对单点系泊系统的影响［D］.大连:大连理工大学，2014.

［8］夏伟宇，朱家明，李德政，等.基于悬链线理论对系泊系统的优化设计［J］.西昌学院学报，2017，31(01):31－35.