橡胶连续混炼粉料混合均匀性仿真及实验研究
2018-05-22张卫锋张福霞汪传生
张卫锋,张福霞,汪传生,王 蒙
(1.青岛科技大学 机电工程学院,山东 青岛 266042; 2.青岛技师学院,山东 青岛 266106)
橡胶及炭黑等物料连续混合输送和称量技术是橡胶连续混炼技术的重要组成部分,炭黑等粉料的混合均匀性和连续配比的精确性决定了橡胶混炼质量的稳定性[1-2].炭黑等粉料的混合和连续称量在橡胶工业一直受到国内外学者的关注,围绕粉体混合的物料输送和称量机理、改善粉体颗粒混合均匀度方面已进行了大量研究,但对于粉体颗粒的运动和混合机理的认识和研究尚不深入,针对粉体物料的连续混合及连续称量方式研究较少且主要集中在间歇式物料混合输送和称量装备上[3].本文针对新型连续式混炼技术和装备要求,分析粉体物几何形状、颗粒直径、颗粒密度等物理特性,建立了粉体物料颗粒模型和动力学模型,并对粉体物料混合进行运动学和动力学分析,研制了实现多种粉体物料的均匀性混合及连续称量工艺和装备.取炭黑、氧化锌、促进剂3种典型混炼粉料进行运动学和动力学分析,研究其混合均匀度,并扩展到多种粉体物料的连续混合研究.
1 粉体颗粒模型和运动模型分析
对于炭黑等粉料混合及输送研究采用离散元素法进行求解,将炭黑等颗粒模型对象划分为相互独立的颗粒单元,并根据各颗粒之间的相互作用力和牛顿运动定律确定单位时间内颗粒单元的受力和位移关系[4-6],通过对每个单元的运动分析,对炭黑颗粒的宏观运动规律进行跟踪计算.根据颗粒对象不同,离散元素法有硬球模型和软球模型两种类型[7-9],硬球模型颗粒之间的碰撞是瞬时的,主要用来模拟如库特流、剪切流中颗粒运动比较快的情况,粉体颗粒在碰撞过程中不会产生显著塑性变形,只考虑两个颗粒的同时碰撞;软球模型主要用来模拟两个颗粒间及两个颗粒以上的碰撞关系.它们之间碰撞时,产生塑性变形,变形碰撞发生在一段时间范围内,利用牛顿第二定律,根据球体间的交叠量可以计算得到颗粒间的接触力[10-12].本研究采用软球颗粒模型和Hertz[13-14]接触模型进行仿真分析及实验研究,针对炭黑及各粉料的结构特性,采用Hertz接触模型表示混合过程中粉体颗粒的相互接触.图1表示颗粒间和颗粒与边界间的Hertz 接触模型,由Hertz接触理论研究颗粒之间的接触刚度-力与位移,假设接触模型的参数之间为线性关系,颗粒间的法向力增量ΔFn与法向位移增量Δun成正比,切向力增量ΔFs与切向位移增量Δus成正比.其中,kn和ks分别表示法向刚度和切向刚度,则有
(1)
在颗粒模型中,炭黑、氧化锌、促进剂颗粒之间存在线性关系,在弹性范围内,任意颗粒模型的应力(σ)和应变(ε)方程为
(2)
式中,σ=Yε.其中,Y为颗粒的弹性模量,由式(1)和式(2)可得颗粒法向刚度的计算公式为
(3)
式中:R1,R2为两相互接触的颗粒半径;b为接触半径;μ1,μ2为两颗粒的波松比;Y1,2为两不同颗粒等效弹性模量,其中,
(4)
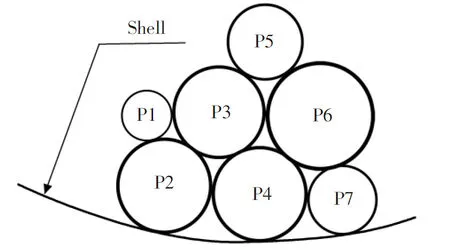
图1颗粒接触及颗粒边界接触
Fig.1 Particle contact and particle boundary contact
由Mindlin[15]研究分析,弹性实体接触碰撞时,可通过法向刚度求解切向刚度,其式为
ks=λkn.
(5)
其中,λ为刚度折减系数,取值范围[2/3,1].假设炭黑、氧化锌、促进剂颗粒之间、颗粒边界之间的接触为Hertz接触,由Hertz接触理论可知,颗粒间的作用力-位移关系方程为
(6)
式中:Y1,2为等效弹性模量:R1,2为颗粒等效接触半径,若Hertz理论初始动能和最大应变能相等,可得线性通用等效法向刚度计算公式,
(7)
根据粉体颗粒模型和Hertz颗粒接触力-位移模型[16-17],结合Pro/E和EDEM软件对粉体物料混合进行模拟仿真,可得到3种不同物理性质颗粒的混合均匀性仿真分析.
2 混合模拟仿真及实验
2.1 物料混合模拟仿真
根据颗粒物理条件定义颗粒模型和接触模型:1)假设颗粒均为理想的球形颗粒;2)颗粒实体间为Hertz-Mindin接触模型;3)定义在仿真时每个网格中有40个颗粒以上为有效网格.建立粉体物料混合装置的物理模型、定义球形颗粒、几何体、仿真区域、创建颗粒工厂、仿真计算等操作.根据模型物理变量参数,分别选取炭黑、促进剂、氧化锌3种比重、粒径相差较大的颗粒物料进行混合模拟,如表1,表2分别定义3种粉料的物理性能参数:泊松比、剪切模量、密度、回弹系数、动摩擦系数、静摩擦系数;设定炭黑半径为0.02 mm,氧化锌半径为0.01 mm,促进剂0.01 mm;并计算3种颗粒质量、体积等颗粒属性.

表1 物理参数
注:颗粒数目影响软件的运算速度和时间.为提高软件运算时间,将颗粒半径等比例增大,减小颗粒数
在EDEM中选择导入实体选项,将自主研发的搅拌机构导入到EDEM中,采用自主设计的螺旋搅拌装置三维模型对物料混合进行仿真分析,将物料通过螺旋搅拌装置在竖直方向上翻转混合,使密度和颗粒度不同的粉料进行混合,3种物料依次加入混合装置内进行搅拌混合,物料混合均匀性随时间的增加而提高,且在40 s后混合性能趋于稳定.对40 s时的混合仿真网格划分并进行混合均匀性评价,计算网格中粉体混合物料的颗粒数,设ni、ρi、ri为混合粉料的第i种粉料的颗粒数、密度、半径,则在混合物料中第i种粉料的质量为
(8)
由式(8)得到各混合粉料在整个混合体系中理论质量,计算出网格内各粉体质量,其仿真模型及结果如图2和表3所示.
表2干燥颗粒间相互作用参数设定(恢复系数/静摩擦系数/动摩擦系数)×10
Table 2 Setting of interaction parameters between dry particles(10 times)

物料钢炭黑促进剂氧化锌钢4/1/04/2/12/1/14/3/1炭黑4/2/13/2/14/4/41/2/0促进剂2/1/14/4/44/2/14/2/0氧化锌4/3/11/2/04/2/04/1/1

图2 粉体物料混合仿真对比图
Fig.2 Hybrid simulation of powder material: (a)20 s ; (b)30 s; (c)40 s

表3 搅拌设备中40 s仿真数据统计
2.2 混合物料均匀性实验
采用粉料混合及称量系统,进行粉体物料混合和连续称量系统物料均匀性实验.任取粉料连续称量系统单位时间内输送和称量的混合粉料进行实验.为了分析物料混合均匀性和称量准确性,取15组实验数据进行分析,验证粉体物料混合均匀性和称量稳定.根据3种粉料的溶解性不同,利用促进剂溶于苯类、醇类,不溶于水及弱碱性溶液;氧化锌溶于酸、氢氧化钠、不溶于和醇类溶液等;普通炭黑不溶于水和有机溶剂特性,采用溶解法将3种物质分别提炼和称量,对实验结果进行数据处理,得到表4实验数据.

表4 混合均匀性实验数据
2.3 连续混炼工艺过程及装备
图3为包含粉体物料连续混合和称量装备的
连续混炼工艺装备.图3中机构8为粉料连续混合及称量装置,该装置将炭黑及10多种小料根据配方要求,通过研发的搅拌装置将多种物料搅拌均匀,采用失重式称量装置通过螺杆将粉料进行连续输送.其螺杆转速由机构7计算的橡胶质量转化成的数字信号确定,并通过粉料连续称量系统的失重传感器信号形成闭环式控制系统;油料系统1根据装置7实现流体控制和固态物料控制的配比称量.将固-粉-液3种不同形态的物料通过不同的称量和输送装置,实现橡胶连续混炼所需要的物料配比和连续称量工艺.
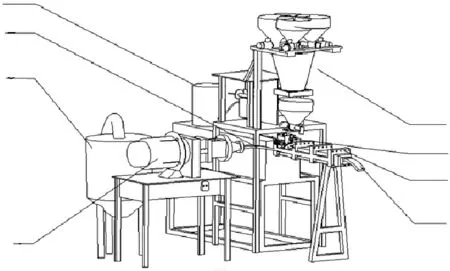
1—油料称量系统; 2—塑炼胶条; 3—气力输送系统 ;4—双坠下片机; 5—成品胶条;6—连续混炼机; 7—胶条牵引测量机构; 8—粉料连续动态称量系统
1—oil weighing system; 2—plastic rubber strip;3—pneumatic conveying system;4—double cone extruder; 5—mixing Rubber strip; 6—continuous mixer;7—rubber strip traction measuring mechanism;8—continuous dynamic weighing system
图3橡胶连续混炼系统
Fig.3 Multi phase continuous weighing system
3 模拟仿真及实验数据对比分析
由表1知,3种物料的质量配比为53.5∶3.5∶1.5.对表4实验数据和表3仿真数据进行分析和处理,得到图4粉体物料仿真和实验均匀性分析图和图5粉体物料质量配比仿真和实验分析图.
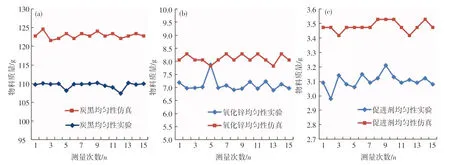
图4混合均匀性数据分析图
Fig.4 Diagram of mixed uniformity data analysis
图4表明,通过研发的上下螺旋翻转式混合装置中进行的仿真和实验结果都有很高的质量稳定性;同时,在粉料实验过程的炭黑均匀性实验误差大于仿真误差,而氧化锌、促进剂实验误差和仿真误差相差较小,说明在实验过程中炭黑粉体颗粒外形结构的复杂性对物料混合的均匀性有较大影响.
图5为按照炭黑和氧化锌、炭黑和促进剂的质量比均匀性仿真和实验曲线.对表3、4和图5进行分析,仿真和实验数据每次称量的结果非常接近3种物料的理论质量配比关系,仿真和实验结果拟合性很高,反应了采用EDEM仿真和进行颗粒混合实验具有很高的拟合性,也说明不同颗粒不同密度的颗粒按照配比实验进行混合的可行性.但在实验过程中,由于颗粒受力的复杂性及颗粒直径的不均匀性,使得实际混合实验误差大于仿真误差.
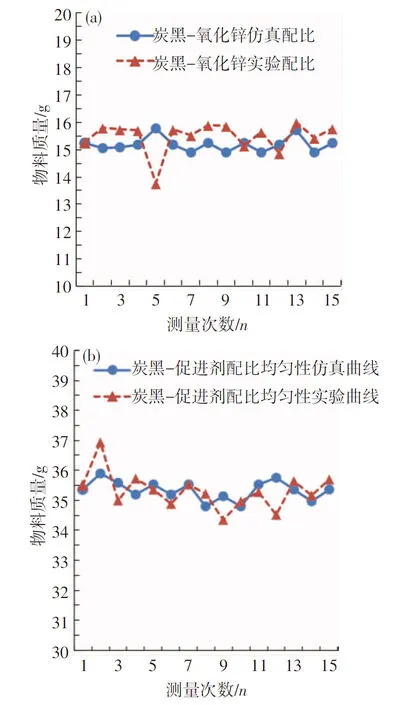
图5物料配比数据图
Fig.5 Diagram of material proportioning data
4 结 论
1)由EDEM模拟仿真和混合实验结果可知,采用新型螺旋上下混合装置可以实现颗粒不同、密度不同的多种粉体物料均匀混合,为多粉体物料的混合和称量提供实验基础和仿真方法.
2)针对混合的炭黑等粉体物料,利用离散元分析创新采用球形颗粒和Hertz接触模型对橡胶混炼粉体物料进行颗粒模型和力-位移受力分析,其模拟仿真结果和实验结果具有很好的拟合性,说明所用的粉体物料颗粒模型和力学模型的正确性和可行性.
3)由混合均匀度数据分析可知,粉体物料混合均匀性实验数据误差大于均匀性仿真数据,表明在橡胶粉体实际混合过程中混合均匀性受到粉粒颗粒不均匀性、摩擦力、工作环境等因素的影响,实现了橡胶连续混炼装置中粉体物料的连续混和及输送,并通过实验分析得到粉体混合过程中实际误差大于理想颗粒的仿真分析数据误差,表明建立实际粉料混合过程数学模型的复杂性.
参考文献:
[1] 杨忠敏.橡胶行业的发展趋势与市场前景[J].橡塑资源利用,2010(6):30-36.
YANG Xiumin.The market prospect and development trend of rubber industry [J]. Rubber & Plastic Resources Utilization, 2010(6):30-36.
[2] 高彦臣,李勇.XLBII一16型小料自动称量系统简介[J].橡塑技术与装备,2003(3):47-50.
GAO Yanchen, LI Yong. Brief introduction of XLBII-16 automatic weighing system for small materials[J].China Rubber/Plastics Technology and Equipment, 2003(3): 47-50.
[3] 汪传生,李利,王海梅等.橡胶混炼技术的现状与发展趋势[J].橡胶工业,2007,5:305-309
WANG Chuansheng, LI Li, WANG Haimei.Thepresent situation and development trend of rubber mixing technology[J]. China Rubber Industry, 2007, 5:305-309.
[4] CUNDALLP A. UDEC-ageneralized distinctelement program for modelingjinted rock[R].U.S.Army: Peter Cundall Associates,European Research Office,1980.
[5] CUNDALL P A. numerical Modelling of Jointed and Faulted Rock[C]//Mechanicsof Jointed and Faulted Rock.Rotterdam:Balkema,1990:11-18.
[6] 王猛.散状物料流动性理论研究及数值模拟[D].太原:太原理工大学,2016.
WANG Meng. Flow theoretical study and numerical simulation of bulk material[D].Taiyuan:Taiyuan University of Technology,2016.
[7] COETZEE C J, ELS D N J. Calibration of discrete element parameters and the modelling of silo discharge and bucket filling[J]. Computers & Electronics in Agriculture, 2009,65(2):198-212.
DOI:/10.1016/j.compag.2008.10.002
[8] 张西良,张建, 李萍萍,等. 粉体物料流动性仿真分析[J]. 农业机械学报, 2008,39(8):196-198.
[9] HUANG H.Discrete element modeling of tool-rock interaction[D] Minneapolis:Univ.of Minnesota, 1999.
[10] SHIMIZU Y, HARTAND R D,CUNDALL P A. Numerical modeling in miero-mechanics via particle methods[C]//Proccedings of the 2nd International PFC Symposium. Leiden: Balkema,2004.
[11] JENSEN R P, BOSSCHER PJ, PLESHA ME,et al.DEM simulation of granular media-structure interface:effects of surface roughness and particle shape[J].International Journal for Numerical Analytical Methods in Geome-Chanics,1999(23):531-547.
[12] HASSANPOUR A, TAN H, BAYLY A, et al. Analysis of particle motion in a paddle mixer using Discrete Element Method (DEM)[J]. Powder Technology, 2011, 206(1): 189-194.
DOI:10.1016/j.powtec.2010.07.025
[13] PORTILLO P M, IERAPETRITOU M G, MUZZIO F J. Effects of rotation rate, mixing angle, and cohesion in two continuous powder mixers-a statistical approach[J]. Powder technology, 2009, 194(3): 217-227.
DOI:10.1016/j.powtec.2009.04.010
[14] HARNBY N, HAWKINS A E, VANDAME D. The use of bulk density determination as a means of typifying the flow characteristics of loosely compacted powders under conditions of variable relative humidity[J]. Chemical Engineering Science, 1987, 42(8):2067.
DOI:10.1016/0009-2509(87)80156-2
[15] MILLER B, O′HERN C,BEHRINGER R P.Stress fluctuations for continuously sheared granular materials[J].Physical Review Letters,1996,77(15):3110-3113.
DOI:10.1103/PhysRevLett.77.3110
[16] 谢刚,李霞,田国辉.固体物料混合过程中混合度的研究[J].黑龙江大学自然科学学报,2003,20(2):111-113.
XIE Gang,LI Xia,TIAN Guohu. Study on the degree of mixedness in mixing of solid materials[J]. Journal of Natural Science of Heilongjiang University,2003,20(2):111-113.
[17] 张卫锋.橡胶混炼多相物料连续称量机理及实验装备研究[D].青岛:青岛科技大学,2017.
ZHANG Weifeng. Study on the mechanism and experimental equipment for continuous weighing of multiphase materials for rubber mixing[D].Qingdao:Qingdao University of Science & Technology,2017.
