基于不同数学模型对某弯道式渠首水沙运动的数值模拟对比研究

吕 科， 赵 涛

(新疆农业大学， 新疆 乌鲁木齐 830052)

1 研究背景

渠首是重要的水工建筑物之一，其作用一方面把河流的水引入渠道，满足农业灌溉、水力发电及生活用水等水利事业的需要[1]；另一方面防止粗颗粒泥沙进入弯道，以免引起弯道冲刷和淤积，以保证弯道正常运行。近几年，国内外学者从各个方面对渠首中弯道特有的水沙运动特性、河床演变规律，进行了广泛深入的研究[2]。

何奇等[3]通过理论分析和物理模型试验，建立了弯道河床床面纵向切应力及横向切应力的计算公式，虽然物理模型结果是直观的，数量可以量化，但是更为昂贵和耗时。随着计算机性能的提高和数值计算方法的发展，在水流流态、泥沙输运、河床冲刷等领域，河流工程研究的计算模型都取得重大进展，成为预测解决实际工程问题的重要手段。例如，李大鸣等[4]建立的冲积河流平面二维水流模型可用于求解断面形态不规则的天然弯道水流的流场，但未考虑弯道环流对纵向平均流速的影响，因此其对宽深比小、曲率大的弯道模拟精度不高；MIKE模型应用于水流的数值模拟，具有较强的前、后处理功能[5]，但并不适用于进行深入研究，一般都在实际工程中使用；Fluent模型目前已在世界多个领域取得广泛应用[6-8]，但是对渠道中的水沙模拟结果不太理想，还需进一步进行验证。

不同于其他水沙数学模型，CCHE是由美国密西西比大学国家水科学及工程计算中心(National Center for Computational Hydroscience and Engineering)研发，针对自由水面、泥沙输运、地形地貌改变和溃坝洪水等问题进行模拟的集成性数学模型。CCHE建立的模型采用实测数据导入功能，根据真实边界勾勒建立模型，能更好地反映天然河道不规则边界地形的真实性。目前，本课题组前期已经采用CCHE模型对乌斯满渠首河段的水流流态进行模拟[9]，结果表明，CCHE模型能够良好地运用于引水枢纽工程的水沙运动数值模拟。

前期研究中，已经证明Fluent中RNGk-ε模型能够对弯道式引水渠首中的水流进行模拟，并具有较高的可信度、精度和适用性[10]。因此本文采用CCHE中涡流抛物线模型和Fluent中RNGk-ε闭合紊流模型对新疆某弯道式引水渠首中的水沙运动进行数值模拟对比研究，以证明究竟何种模型对渠首中弯道水沙二相流的模拟更具针对性、高效性及可靠性。

2 模型概述

2.1 数学模型

Fluent中RNG紊流模型方程中的常数由理论推导得出，并非由试验方式确定，耗散方程中的系数C*ε体现了平均应变率对耗散项的影响，因此对高速水流的各项异性模拟较好。但求解方程较多、计算量较大，且大多为经验公式，精度较低。CCHE涡流抛物线模型将RNG中的Gk，由层流速度梯度产生的湍流紊流耗散项直接率定为沿垂线方向的平均雷诺应力，且CCHE模型加入科氏力的影响，对弯道流场中可能出现的适度旋流有较高的模拟结果。抛物线模型控制方程如下:

(1)

(2)

(3)

αdωsk(C*k-Ck)

(4)

(qbk-qb*k)/L=0

(5)

2.2 物理模型

该渠首采用人工弯道式分水枢纽，主要由上游河道整治段(包括左、右岸导流护堤)、人工弯道、泄洪闸(3孔)、冲砂闸(3孔)和进水闸(3孔)组成，泄洪闸保证泄水流量为70 m3/s，冲沙闸、引水闸设计流量均为35 m3/s。该渠首模型的模拟长度约为550 m，其中上游河道整治段约为150 m，人工弯道约为250 m，下游河道约为150 m。物理模型采用正态模型[11]，几何比尺为λl= 30，通过试验，可测得在不同工况下的水面高程、水流流速及弯道水沙冲淤平衡时典型断面泥沙淤积等试验数据，可以为数学模型模拟结果对比提供可靠依据。其弯道枢纽模型平面布置见图1所示。

3 数值模拟

3.1 网格划分

CCHE模型采用结构化网格的有限元法，自带网格处理模块，优化网格质量，在模拟复杂地形、复杂边界的水流运动中显现出一定优势[12]，图2为CCHE计算模型网格示意图。

图1 弯道枢纽模型平面布置图(单位：m)

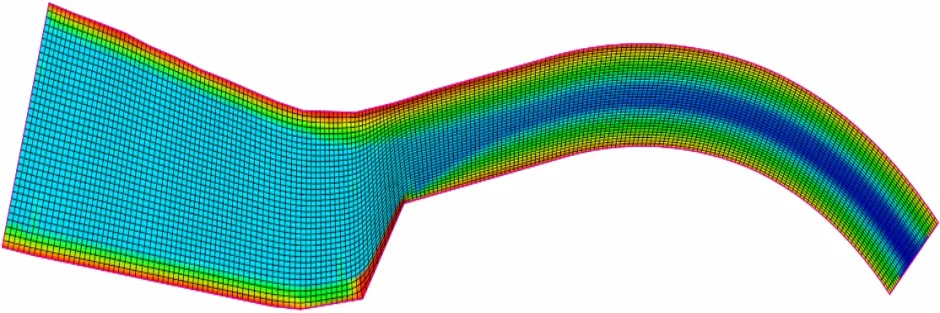
图2 CCHE计算模型网格示意图

Fluent模型采用有限体积法，建立结构网格并采用网格变形技术解决边界问题，图3为Fluent计算模型网格示意图。

3.2 边界条件

CCHE模型进口边界给定流量，出口边界给定水位高程，设置边壁无滑移，CCHE模型自动考虑底层产生的涡流影响。在模拟河流中，对于刚性盖子边界的自由表面，CCHE模型默认为自由液面边界。

Fluent模型设置水流进口类型为velocity-inlet，出口类型为outflow，边壁设定为无滑移边界条件，黏性底层采用壁面函数进行处理。对于自由液面的处理方式，Fluent模型采用批量跟踪法的VOF算法进行计算。

4 模拟结果分析

在模拟过程中，CCHE和Fluent模型的建立均通过对不可压缩N-S方程的迭代离散来实现。对边界和初始条件及可能影响河流泥沙输运的参数采取相同预设，并在模拟运算的过程中CCHE及Fluent均得到收敛的解。因此，两类模型所存在的差异可能来自于数学推导、数值解法、程序语言或网格质量的优劣。

4.1 水面线

弯道水流受到离心力的作用，使凹岸水面壅高，凸岸水面降低，从而形成横向比降[13]。图4、5分别为在某工况下，凹岸、凸岸两侧水面高程的数值模拟结果与物理模型试验结果对比图，表1为弯道水面高程数值模拟结果与物理模型试验结果对比。

图3 Fluent计算模型网格示意图

由表1、图4中可以看出两种模型均可得到弯道水流自由水面的基本变化形态，具有显著的水面横比降，但不同数学模型计算结果存在差异：Fluent模型最大横比降出现在弯顶处，但随水流流出弯道后消失，不能充分体现弯道离心力的作用；CCHE模型计算结果显示，弯道后段，主流水面横比降依旧比较明显，更确切地反映出水流受离心力作用发生的偏移现象，该模型计算结果与实测值较为吻合，说明CCHE模型模拟弯道水流自由表面沿程变化精度较高。总体来说，在弯道的进口和出口部分，两种数值模拟的结果相差不大，但是在弯道的主体部分，CCHE模拟结果的精度明显高于Fluent模型的计算结果。

图4凹岸水面高程数值模拟结果与物理模型试验结果对比图5凸岸水面高程数值模拟结果与物理模型试验结果对比

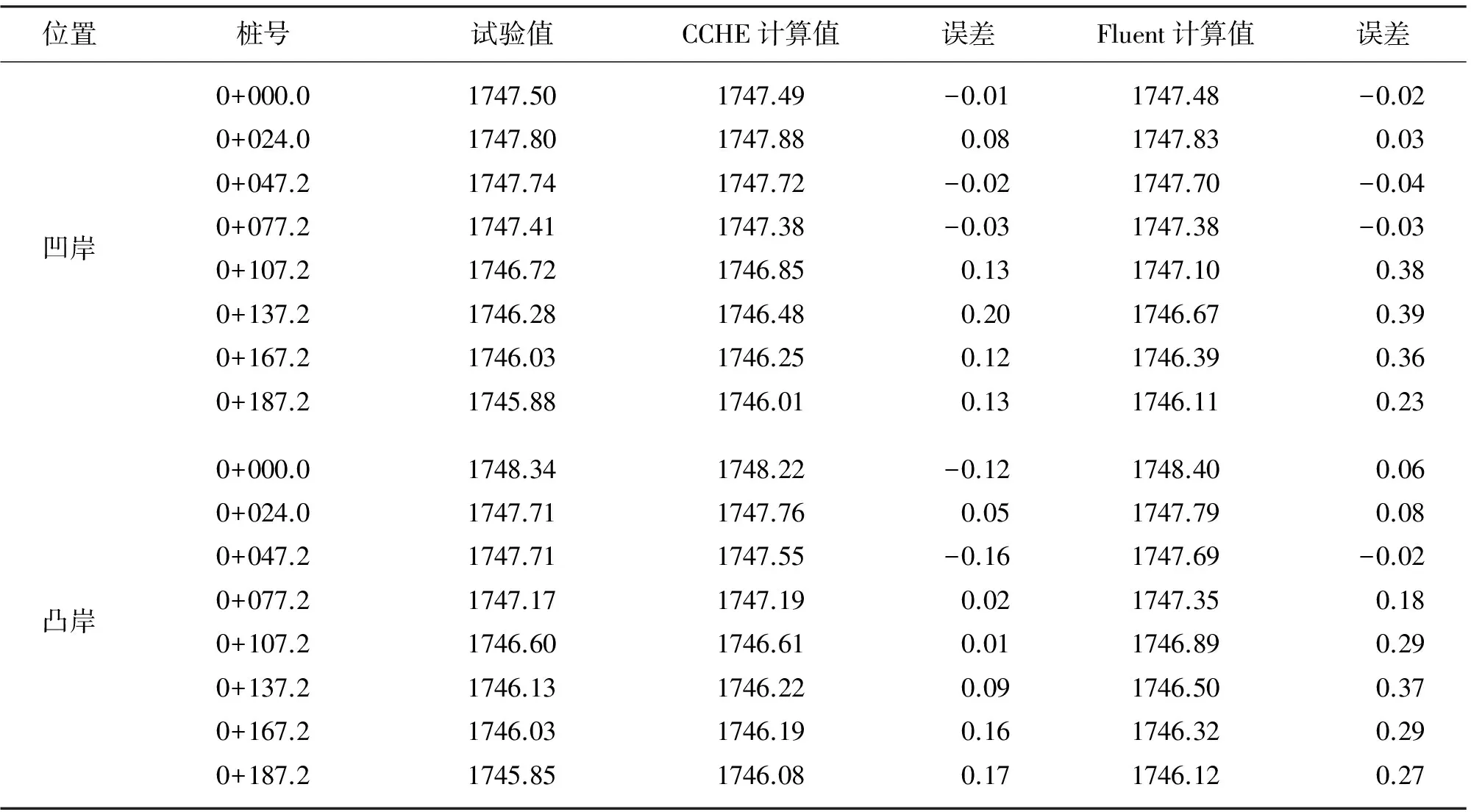
表1 弯道水面高程数值模拟结果与物理模型试验结果对比 m

4.2 弯道断面泥沙淤积

由于弯道横向环流的作用，凹岸受到冲刷，形成水深流急的深槽，而凸岸不断淤积，形成水浅流缓的浅滩[14]。浅滩淤积形态与河床形状有关[15-17]，在环流作用下，弯曲型河道凸岸下游一侧容易发生淤积，凹岸受到冲刷。本文采用了两种模型模拟弯道内的泥沙运动及河床的纵向变形，通过与物理模型泥沙淤积数据进行对比来验证弯道的合理性及模型的准确性。

CCHE模型设置泥沙浓度为入口边界，并设置一系列泥沙输运参数，其中包括泥沙颗粒大小、河床分层数目和混合层厚度等。在考虑河床糙率、泥沙空隙率等因素后，通过求解对流扩散方程来模拟悬移质沙输运[18]，悬移质沙饱和系数经验值一般设置为0.04。

Fluent模型设置为固液两相流，设置泥沙流速为入口边界，对泥沙颗粒大小、压强、浓度等参数设置与CCHE模型相同，模拟结果如下：

图6、7为弯道入口处整体冲淤情况。随着泥沙的推移，在弯道0+092 m断面可以观测到凹岸存在明显冲刷效应，并在凸岸边坡部位开始产生淤积。与典型断面实测数据相比，Fluent模型在弯道初段对泥沙输运的模拟结果及泥沙初始淤积点的拟合度与试验实测数据具有较大的差异；在CCHE模型模拟弯道泥沙淤积云图中，蓝色代表水流冲刷深度，红色则代表泥沙的淤积高度。从图8可以看出，在弯道进口段，没有明显淤积，CCHE模型模拟结果很好的耦合了试验结果，说明所建立的CCHE模型能够比较准确地模拟该渠首弯道前部的河床演变活动。弯道中后段，冲刷与淤积效应大幅度增加，并在出口断面达到最大值。凹岸最大的冲刷深度为0.9 m左右，凸岸淤积严重，并展现入侵趋势。由图6、7可以看出，两类模型模拟弯道中后段泥沙的冲淤趋势均与试验结果基本一致。

图6 CCHE模型下泥沙淤积云图

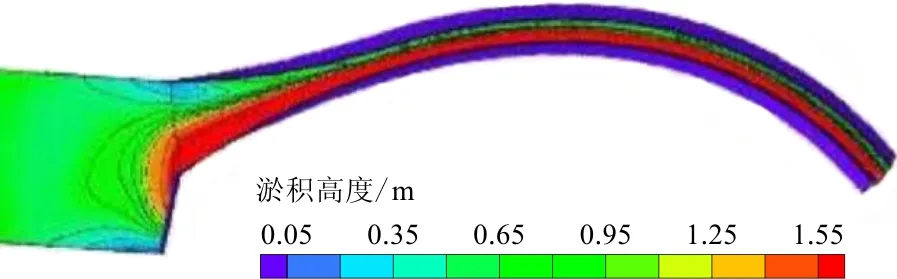
图7 Fluent模型下泥沙淤积云图

综上所述，Fluent中RNGk-ε双方程湍流模型对泥沙淤积的模拟结果与物理模型试验结果相比存在一定误差，对泥沙冲淤的模拟具有一定的局限性，只有针对较大范围的泥沙淤积模拟才具有较高的拟合度。与之相比较，CCHE在小规模泥沙淤积模拟中同样具有较高的精度，并具有更高的普适性。CCHE的开发者通过对泥沙非平衡输运模型的提出，改善了弯道二次环流对泥沙输运模拟过程所造成的影响。因此，CCHE模型不仅解决了小规模的泥沙冲淤模拟吻合度不足的问题，并能够充分展现弯道环流作用下的泥沙冲淤效果，提供了基本定性的合理结果。

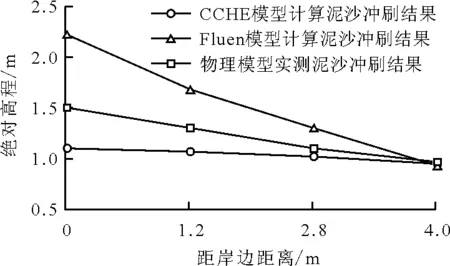
图8 0+024 m断面泥沙淤积数值模拟结果与物理模型试验结果对比图

4.3 模拟耗时

对渠首整治段、弯道及下游河道的水流流态进行模拟，在保证计算精度的情况下，最终确定CCHE的网格数量约为83 200个，Fluent为68 798个，两个模型的计算网格数量大致相同，图9为Fluent计算某工况下关闭冲沙闸水流达到稳态后的速度分布图。

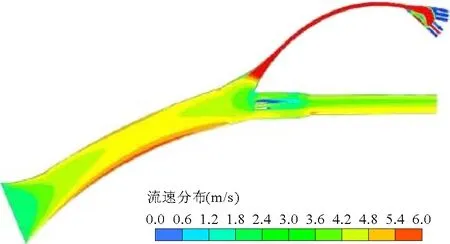
图9 Fluent计算某工况下关闭冲沙闸水流达到稳态后的流速分布图

在实际工程中，采用数值模拟的方式为工程提供设计依据时，不仅对其计算精度有较高要求，还应考虑其计算耗时等因素。将CCHE模型和Fluent模型同时对该渠首进行水流数值模拟。模拟结果显示，CCHE模型模拟该渠首水流运动过程整体时长约为480 s，当运行至200 s左右，水流基本达到稳定状态，模拟结果已经和稳定状态水流流速分布结果基本吻合；而Fluent模型在计算运行344 s后水流才达到稳定状态，并且模型实际运行总时长约1 600 s，模拟所需的时间大幅度延长。结果表明，相对于Fluent模型，CCHE模型不仅收敛速度快，且实际模拟时间短。

究其原因，是因为与被广泛应用的Fluent模型相比，CCHE模型计算控制方程数量较少，能减少大量运算工作，其运行速度大约为Fluent的4倍。可见CCHE模型在满足计算精度的同时，计算效率较高，节约时间。

5 结 论

本文通过两种不同的数学模型对复杂弯道式渠首水流泥沙运动进行模拟，并通过与实测结果对比，得出以下结论：

(1)CCHE和Fluent模型均可用来模拟水沙运动问题，但各自的精度存在差异，对两类模型计算得出的水面高程、泥沙淤积等模拟结果进行比较分析得出，Fluent模型计算结果误差相对较大，CCHE模型与物理模型结果吻合度较高。

(2)分析水面高程对比图得出，两类模型均可模拟弯道水流自由水面沿程变化的大致形态，存在一定水面横比降，但相比于Fluent模型，CCHE模型模拟结果与实测结果虽然存在误差，但最大误差均在10%之内，这说明CCHE模型能够提供更真实、可靠的模拟结果；在模拟弯道泥沙横向输运时，CCHE模型的模拟结果更符合实际规律，在入口横断面处，没有明显泥沙淤积现象，随着水沙进入弯道中部，水流受到强烈离心力作用，产生弯道环流，导致在出口断面处产生明显的凹岸冲刷，凸岸淤积现象；在计算耗时方面，实际模拟时间证明，CCHE模型能够更快地使方程收敛，计算用时只需Fluent模型用时的1/4。

综上所述，CCHE2D模型能够稳定、高效地对顺直形渠道、“S”形弯道以及水利枢纽附近涡流的产生进行模拟。但在后期模型模拟中，为达到更精确的数据要求，更好地模拟环流作用下的流速矢量分布和水沙变化过程，建议采用CCHE3D模型进行模拟。

参考文献：

[1] 王 庆,郭德发.新疆人工弯道式引水枢纽的设计与运行[J].水资源与水工程学报,2003,14(4):48-50+53.

[2] OUTEIRO J C, UMBRELLO D, M'SAOUBI R.Experimental and numerical modelling of the residual stresses induced in orthogonal cutting of AISI 316L steel[J].International Journal of Machine Tools & Manufacture,2006,46(14):1786-1794.

[3] 何 奇,王 韦,蔡金德.环流非充分发展的弯道床面切应力计算[J].泥沙研究,1989(3):66-74.

[4] 李大鸣,陈 虹,李世森.河道洪水演进的二维水流数学模型[J].天津大学学报(自然科学与工程技术版),1998(4):439-446.

[5] 枚 龙.基于MIKE模型在内河航道整治中应用研究[D].重庆:重庆交通大学,2014.

[6] 王福军.计算流体动力学分析:CFD软件原理与应用[M].北京：清华大学出版社,2004.

[7] 戴会超.水利水电工程水流精细模拟理论与应用[M].北京：科学出版社,2006.

[8] WANG Bencheng,ZHAN Jiemin, YU Linghui,et al.Numerical Simulation for flow characteristics of suspension height in suction sump of pump station[J].Water Resources & Power,2012,30(11):70-72.

[9] 徐 乐,牧振伟,李园园,等.基于CCHE模型的乌斯满引水枢纽水流数值模拟[J].水资源与水工程学报,2015,26(5):172-176.

[10] 冯丽华,吉庆丰.三种紊流模型数值模拟明渠弯道三维水流的比较[J].灌溉排水学报,2008,27(6):55-57.

[11] 杜丽霞.典型弯道水流中的水沙二相流三维数值模拟研究[D].新疆:新疆农业大学,2013.

[12] WANG S S Y,WU Weiming.Computational simulation of river sedimentation and morphology: A review of the state of the art[J].国际泥沙研究(英文版),2005,20(1):7-29.

[13] 戴文鸿,苗伟波,高 嵩,等.弯道水流运动及床面变形数值模拟研究进展[J].南水北调与水利科技,2014,12(3):121-126.

[14] 王 庆,郭德发.新疆人工弯道式引水枢纽的设计与运行[J].人民长江,2004,35(1):13-14．

[15] 易雨君,王兆印,张尚弘.考虑弯道环流影响的平面二维水沙数学模型(I)——模型的建立[J].水力发电学报,2010,29(1):126-132.

[16] 钱 宁.河床演变学[M].北京：科学出版社,1987.

[17] 张瑞瑾.河流泥沙动力学[M].北京：中国水利水电出版社,1989.

[18] 吴凤元,樊赟赟,梁 力,等.悬移质泥沙运动过程模拟分析[J].东北大学学报(自然科学版),2016,37(3):431-434.

[19] 韩其为.非均匀悬移质不平衡输沙的研究[J].科学通报,1979(17):804-808.