PSO-RBF神经网络在导水裂缝带高度预测中的应用

2018-05-22刘国发王玉振

中国矿业 2018年5期

刘国发，王玉振

(河南水利与环境职业学院，河南郑州 450011)

0 引言

水体下采煤时，导水裂缝带高度直接影响到防水安全煤柱留设的安全问题。目前，导水裂缝带高度常用的获取方法有现场实测法、模型实验法、经验公式类推法等[1]。现场实测法耗费大量的人力物力，耗资大，工程量大，不易实施；模型实验法容易受模型结构的简化问题及模型参数如何正确选择等多方面因素的影响；经验公式类推法需要决策者具有非常丰富的实践经验，往往取值与实际偏差较大。为了解决这些问题，王正帅等[2]和藺哲渊[3]采用支持向量机的方法建立了导水裂缝带高度预计模型；刘立民等[4]和陈凯等[5]分别分析了二元统计方法和趋势面分析法在导水裂缝带高度预计中的适用性；赵德深等[6]引用了熵的概念，以熵为权重，结合层次分析法对导水裂缝带高度进行了预计研究；黄欢[7]将PLS算法和BP神经网络相结合，建立了导水裂缝带高度预计模型。这些模型都取得了较好的预计效果，尤其是神经网络模型，更是在瓦斯浓度预测[8]、绝缘子污秽智能诊断[9]和概率积分法预计参数求取[10]等方面得到了很好的应用。但应用PSO-RBF神经网络模型预计导水裂缝带高度等方面的文献尚不多见。在综合分析导水裂缝带的主要影响因素的基础上，本文构建了基于PSO-RBF神经网络的导水裂缝带高度预计模型，并对其进行了分析和验证。

1 基于PSO-RBF神经网络的构建

1.1 RBF神经网络基本模型

与传统神经网络一样，RBF神经网络也具有输入层、隐含层和输出层等3层结构。但与传统神经网络不同的是，RBF神经网络只有一层隐含层，且采用RBF径向基函数作为隐含层的激励函数。在实际使用中，高斯函数通常被选用为RBF径向基函数，如式(1)所示。

(1)

ci、ri是函数运行的重要参数，其取值的优劣直接影响到网络的收敛速度及其预测能力，故这两个参数需要进行优化处理，以便选取其最优解。

1.2 PSO优化算法

基于鸟类找寻食物的行为，提出了基于群体的优化算法—PSO优化算法。PSO优化算法具有简单有效的迭代规则，可通过追寻局部最优解来寻求全局最优解，然后利用适应度来分析评价全局最优解的优劣。目前PSO优化算法已经广泛应用于神经网络训练等应用领域。

PSO优化算法的基本思路：假设有m个粒子，每个粒子具有n维位置信息，故第i个粒子的位置信息可采用三个n维向量来表示。

当前位置：X=(xi1，xi2，…，xin)；

历史最优位置：Y=(yi1，yi2，…，yin)；

速度：V=(vi1，vi2，…，vin)。

粒子在n维空间搜索目标。经过多次循环迭代的过程后，当某粒子到达其历史最优位置时，该粒子被称为个体最优粒子；与此相似，当所有粒子经迭代过程达到历史最优位置时，称为全局最优粒子。在粒子运动过程中，其位置信息可通过式(2)进行更新。

(2)

1.3 基于PSO的RBF神经网络优化模型

选取径向基的中心ci和宽度ri作为优化参数。基于PSO的RBF神经网络优化算法步骤如图1所示。

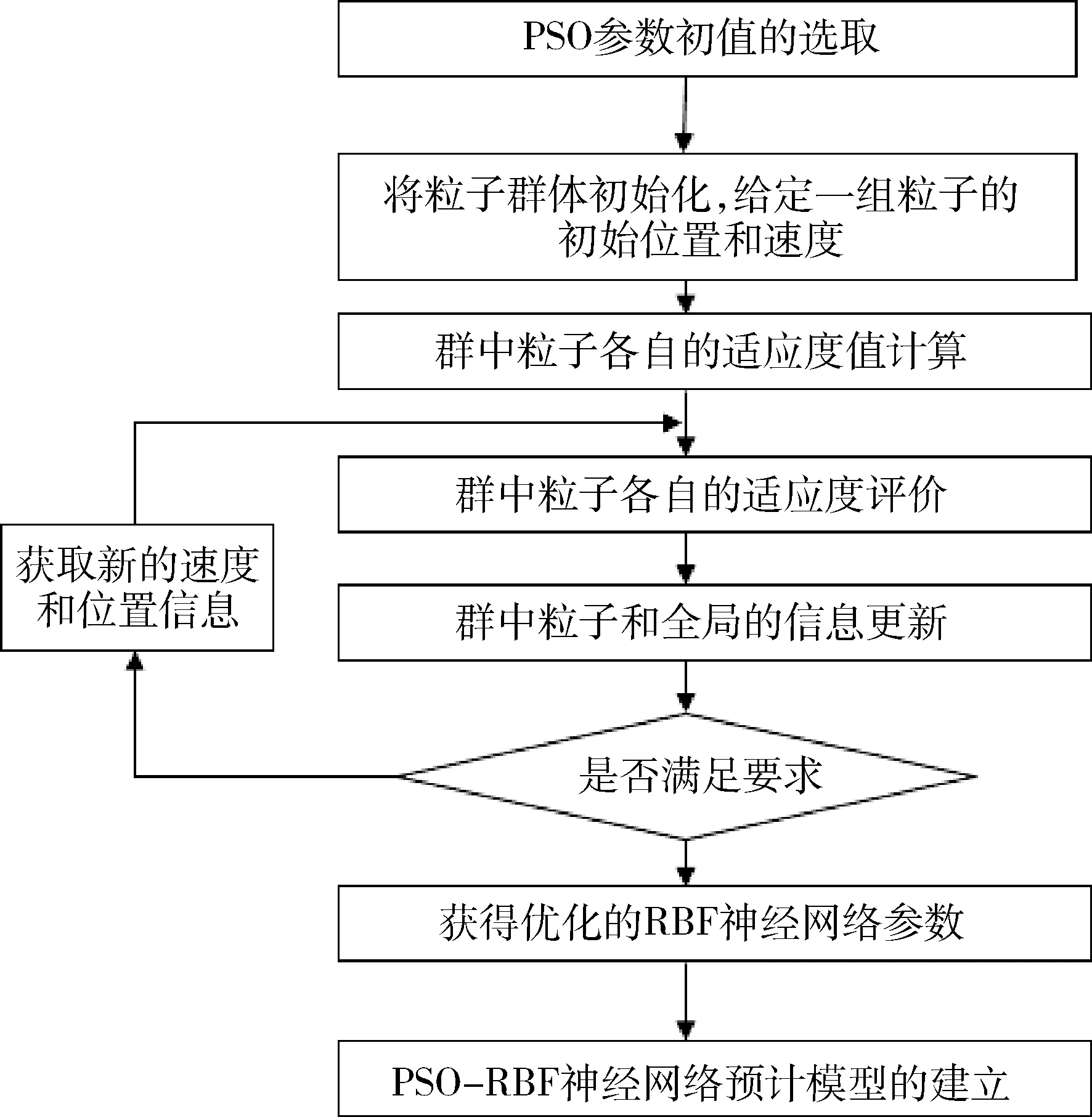
图1 预计模型建立步骤

2 导水裂缝带高度影响因素分析

通过对实测数据和理论分析，并结合沉陷理论可知，导水裂缝带发育高度主要与上覆岩层岩性、煤层开采厚度、采动程度、采深、煤层倾角和煤层分层开采的层数等地质采矿条件有关。

1) 上覆岩层岩性及岩层结构。上覆岩层的岩性越硬，采空区上方的导水裂缝带高度越大；反之，采空区上方的导水裂隙带高度越小。岩层结构可大致分为坚硬-坚硬、坚硬-软弱、软弱-坚硬和软弱-软弱四种，且其综合岩性依次降低，导水裂缝带破坏高度依次减小。为便于计算，将四类岩层组合方式依次量化取值为0.8、0.6、0.4和0.2。

2) 采厚。煤层采出厚度越大，采空区上方的导水裂缝带高度越大。

3) 采动程度。在非充分采动阶段，采动程度越大，导水裂缝带发育越充分，导水裂缝带高度越大。

4) 采深。采深越大，煤岩原岩应力越大，采后产生的导水裂缝带高度越大。

5) 煤层倾角。当其他地质采矿条件大致相同的情况下，煤层倾角小于45°时，煤层倾角越大，导水裂缝带高度越大；当煤层倾角大于45°小于60°时，煤层倾角越大，导水裂缝带高度越小。

6) 煤层分层开采的层数。煤层分层开采的层数越多，采空区上方的导水裂缝带高度越小。

3 PSO-RBF神经网络导水裂缝带高度预计模型的构建

3.1 RBF神经网络的构建

RBF神经网络的三层结构如图2所示，选取如下：①输入层。选取上覆岩层岩性及岩层结构、采深、采厚、煤层倾角、分层开采层数和采动程度等6个导水裂缝带高度影响因素作为输入层神经元；②隐含层。第二层为网络模型的隐含层；③输出层。第三层为输出层，选取导水裂缝带高度一个神经元。

3.2 学习和训练样本的选择

选取以下25个工作面实测数据作为模型学习、训练和检测的样本。每一个样本都包括上覆岩层岩性及岩层结构、采深、煤层倾角、采厚、采动程度、分层开采层数等6个导水裂缝带高度影响因素和1个导水裂缝带高度数值，如表1所示。1～20号数据为学习样本，21～25号数据为测试样本。采用1～20号数据对PSO-RBF神经网络模型进行学习训练，然后采用21～25号数据对模型的适应度进行测试。

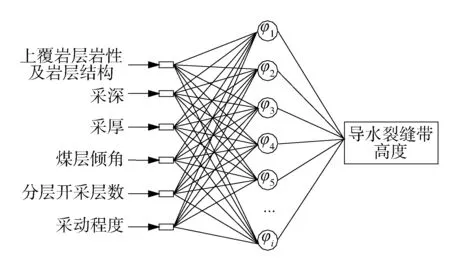
图2 RBF神经网络模型

序号工作面名称覆岩岩性及岩层结构采深/m采厚/m倾角/(°)工作面尺寸/m分层开采层数导水裂缝带高度/m1杨庄矿坚硬⁃软弱3201 7665127 52孔集矿坚硬⁃坚硬20087689148 03大柳塔1203软弱⁃软弱49451351454赵坡矿软弱⁃坚硬1201 2875131 005范各庄软弱⁃坚硬1733 82070226 76大平矿软弱⁃坚硬46711 4820712287新集一矿软弱⁃软弱3298 18134183 98杨村坚硬⁃坚硬272811 51201629五阳坚硬⁃坚硬2136 28167291 710马家沟坚硬⁃坚硬209 54 53077247 311济宁1301坚硬⁃软弱4796 64170166 612鲍店1303坚硬⁃坚硬434 68 78153164 513补连塔31401坚硬⁃坚硬260 945 22265 5115414鲁西107软弱⁃坚硬3415 3699 524515鲍店1310坚硬⁃软弱418 68 76198165 516灵新L3414软弱⁃坚硬113 32 4514 5188 8134 9817华丰1409坚硬⁃坚硬10246 532180175 618新集二矿软弱⁃坚硬4755 132814914519潘二1102坚硬⁃坚硬2701 81810013320柳花岭404坚硬⁃坚硬892 03769145 8621东滩4308坚硬⁃坚硬433603013522百善664软弱⁃软弱1683 15 5137127 823祁东7114坚硬⁃软弱5203121741102 324鹤壁八11033软弱⁃软弱225623174358 425东欢坨2186坚硬⁃软弱4203 72370156 8

3.3 模型学习和测试的过程

调用Matlab软件工具箱中的newrb函数，进行模型的学习和训练。具体步骤如下：①采用POS算法，经过多次迭代，获得最优的径向基函数中心和宽度；②采用1～20号数据对RBF神经网络模型进行学习训练；③将模型的收敛精度设置为0.0001，进行模型循环迭代，直至满足精度要求结束；④利用21～25号数据对已经学习训练好的模型的适应度进行测试。

通过图3可知，当迭代次数达到480次左右时，模型收敛精度即可达到0.0001。

3.4 模型预计能力测试

为检验预计模型的有效性，将采用1～20号数据学习训练好的模型用于21～25号数据的预计中。为了分析预计模型的预计效果，采用传统BP神经网络模型预计结果作为对照，预计模型预计结果见表2。

学习训练结束后，1～20号学习样本的拟合程度很高，如图4所示。

从表2可知，PSO-RBF神经网络预测模型在导水裂缝带高度预计时具有较高的预计精度，实测值与预计值的最大相对差值为7.43%，最小为1.41%，满足沉陷工程精度需求。

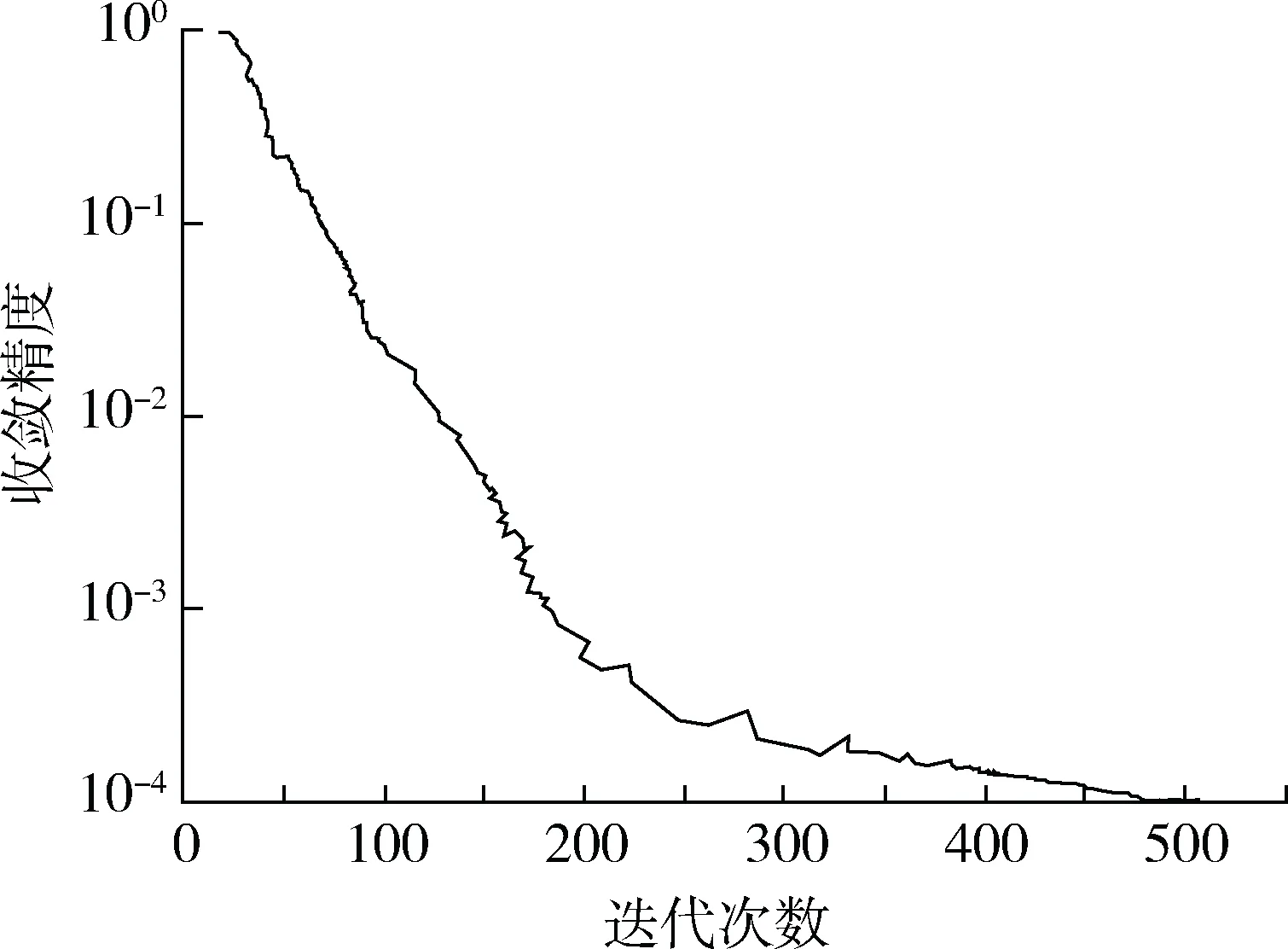
图3 学习训练进程

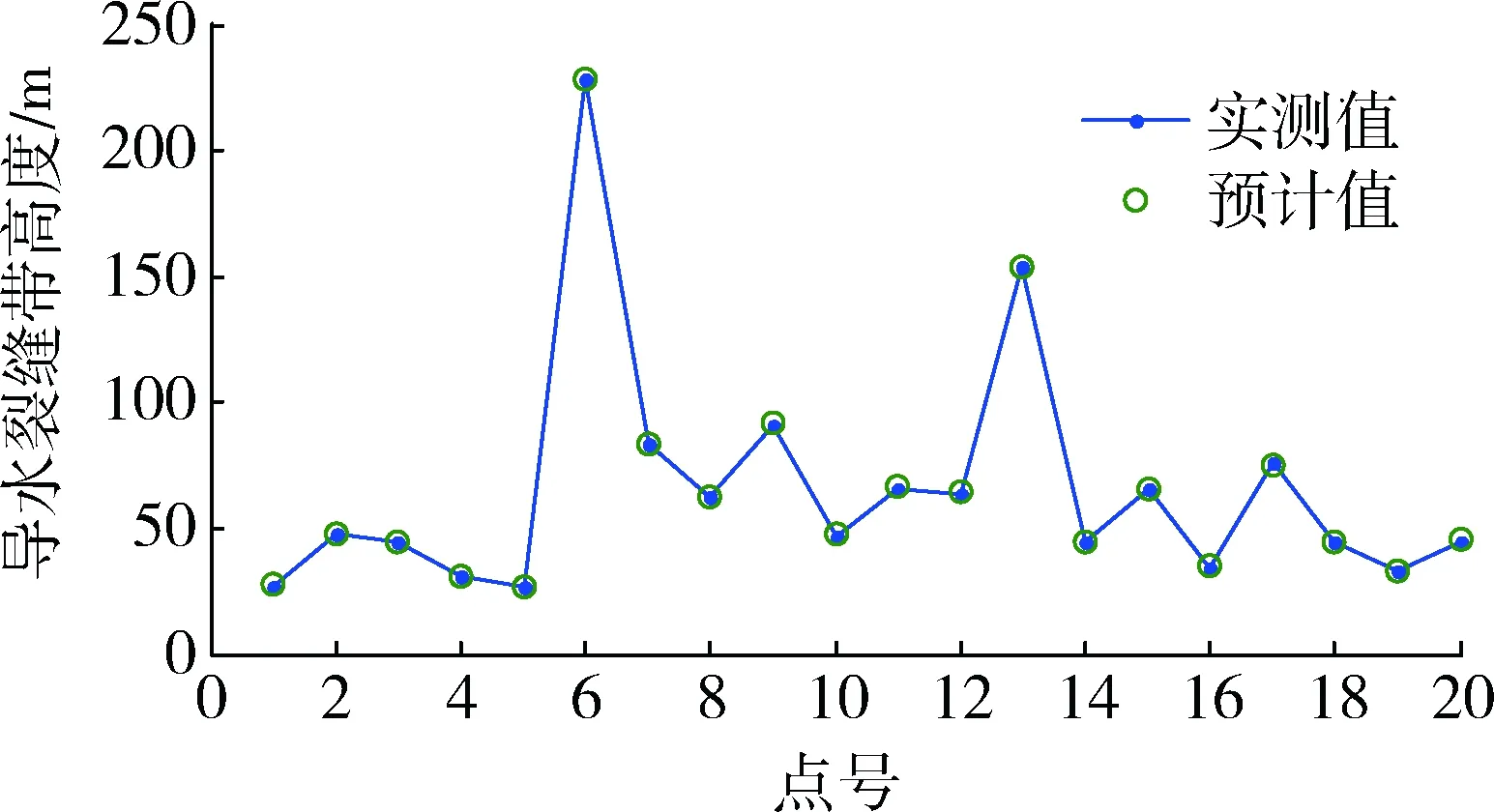
图4 学习训练效果图

序号观测站实测值/mBP预计值/m绝对差值/m相对差值/%PSO⁃RBF预计值/m绝对差值/m相对差值/%21东滩43083531 43 610 2932 42 67 4322百善66427 832 8-5-17 9926 51 34 6823祁东7114102 396 16 26 0699 52 82 7424鹤壁八1103358 462 8-4 4-7 5361-2 6-4 4525东欢坨218656 854 12 74 7557 6-0 8-1 41