数据包络分析研究热点综述

张宏军，徐有为，程 恺，张 睿，尹成祥

陆军工程大学 指挥信息系统学院，南京 210000

1 引言

数据包络分析（Data Envelopment Analysis，DEA）是以线性规划为基础，对同类型的多输入、多输出决策单元（Decision Making Unit，DMU）进行相对有效性评估的非参数系统分析方法，属于运筹学、管理科学和数理经济学交叉研究[1]的领域。其中，同类型条件要求所有的DMU具有相同的输入和输出指标、相同的任务和目标，以及相同的外部环境[2]。DEA根据各DMU的观测数据，判断各DMU的相对有效性，本质是判断DMU偏离生产前沿面的程度[3]。相较于传统的生产函数理论，应用DEA对同类型多输入、多输出DMU分析时，不需要预先估计参数，由于量纲无关性、无假设权重等特点，DEA在避免主观因素和简化算法、减少误差[1]等方面有着巨大的优越性。

DEA的研究历史最早可追溯到1957年Farrell提出的包络思想[4]，1978 年由 A.Charnes和 W.W.Cooper等人[5]正式提出。中国学者研究DEA模型始于1986年，1988年魏权龄公开出版了关于DEA模型的第一本专著[6]。在将近40年的研究进程中，DEA得到了迅猛发展，ISI Web of Science Core Collection（Web of Science核心合集）、Engineering Village（EV）和中国科学引文数据库（CSCD）等各大数据库中相关文献检索数量均达到上千篇，已经有数以万计关于DEA的研究论文、工作报告和博士论文等发表。

DEA跨学科研究已经深入到应用经济学、管理科学与工程等多个学科，在多个领域的定量检测均取得了满意的效果，表1列举了部分应用领域和相关文献。事实说明，DEA已经引起国内外大批研究人员的关注。

本文在阐述DEA基本思想和模型的基础之上，梳理了近年来DEA领域研究的主要成果，重点分析讨论了

表1 DEA应用文献分类汇总

DEA当前的研究热点，并对其未来研究趋势给出了预测。

2 基本思想和模型

假设有n个决策单元，m个输入指标和s个输出指标，分式规划下，面向输出的CCR模型如公式（1）所示：

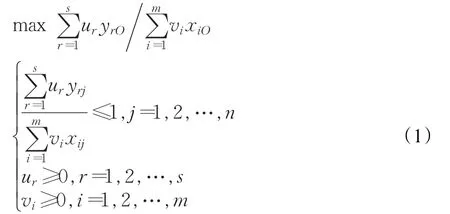
其中，xij、yrj分别表示DMUj的第i种投入和第r种产出，vi、ur分别是对输入、输出的度量。规划的最优值代表了该DMU的相对有效性。如果最优值是1，说明该决策单元是DEA有效或DEA弱有效的，否则是无效单元。

根据Banker[27]提出的生产可能集（PPS）的定义：

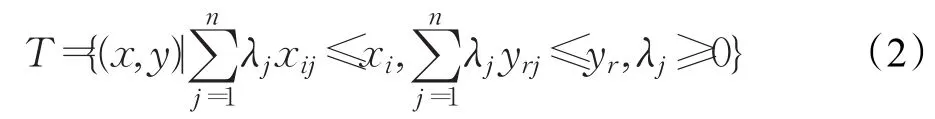
定义 T={(x,y)|产出y可由投入x生产产出}为生产可能集，CCR模型对应的生产可能集如公式（2）所示：称作规模收益不变假定生产可能集，该生产可能集由平凡公理、凸性公理、锥性公理、无效性公理、最小性公理组成的公理体系[5]确定。

应用DEA模型分析相关效率问题时，通常分为确定评价目标、选择同类型的决策单元、建立输入输出指标体系、选择合适的DEA模型、评价分析DEA结果并给出相应结论等一共5个步骤。另外有经验公式[28]，在满足n≥max{3(m+s),m×s}条件下，DEA模型具有稳定和可接受的结果。

3 DEA扩展模型

当下DEA模型已经成为多投入多产出情况下决策单元相对有效性和规模收益等方面应用最为广泛的数理方法之一[2]，基于不同生产可能集假定的模型[29-32]、基于不同偏好的DEA模型[33]、基于不同测度的DEA模型[34-35]等先后被提出。本文将当前DEA研究热点概括为：两阶段DEA、效率排序DEA、随机DEA和其他相关扩展问题。下面针对以上研究热点，分别介绍各方面的模型，并对模型进行比较分析。

3.1 两阶段DEA模型

两阶段DEA模型的提出是为了解决类似供应链系统中内部供应链效率分析问题，它打破了传统DEA将DMU看做“黑箱”的假设，将中间输出/输入定义为中间措施[36]。两阶段DEA模型主要分为3类：独立两阶段模型、连接两阶段模型和关系两阶段模型。

独立两阶段模型[36-38]是两阶段DEA的最初模型。Wang等[36]分析了22家银行的效率，定义第一阶段为IT相关的增值活动并产生资产，第二阶段银行使用资产作为资金来源投资证券和提供贷款。Seiford和Zhu[37]应用同样的方法评估美国顶级商业银行的效率，在盈利阶段银行消费投入并产生利润，在营销阶段利用利润创造市场价值。

连接两阶段模型是独立两阶段模型的改进，包括价值链模型[38]（连接两阶段模型的先驱代表）和网络模型[39]。网络模型从空间上打开“黑箱”，可以评价DMU单元整体和内部各部分的相对有效性。Avkiran[40]使用网络模型来研究阿拉伯联合酋长国的国内商业银行，评估了银行内部多个独立利润中心之间的效率。同样的方法、类似的结构还用于研究NBA球队[41]、中国台湾银行[42]、电厂绩效[43]和中国台湾旅游宾馆[44]的有效性评估。

关系两阶段模型是在连接两阶段模型基础上的又一改进。Kao等[45]认为两种效率之间存在乘法关系并构建了相应的乘法两阶段模型。Chen等[46]采用加权求和的方法构建了加法两阶段模型。Wang等[47]指出可以采用调和平均数，并将其应用到一般中国台湾保险公司得到两阶段的综合相对有效性。Wang K[48]等同样应用加权求和的方法，评估了中国商业银行的效率。

3.1.1 独立两阶段模型

面向输出，规模收益不变的独立两阶段模型如公式（3）所示。

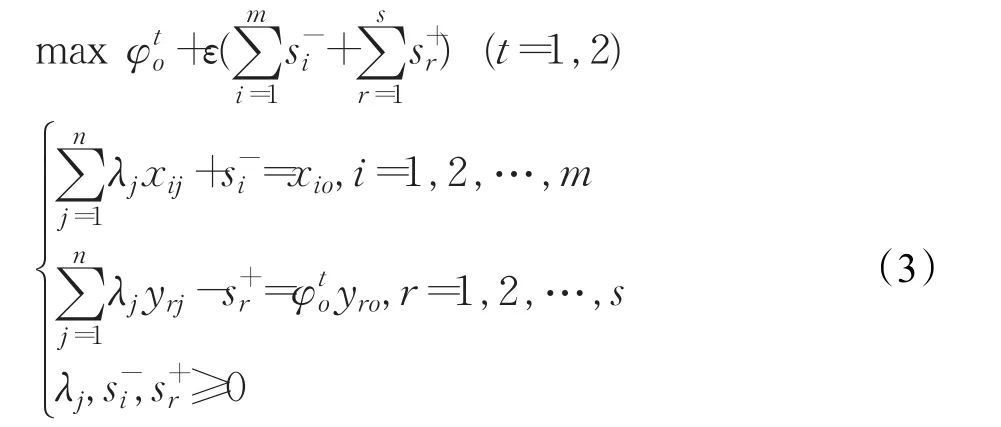
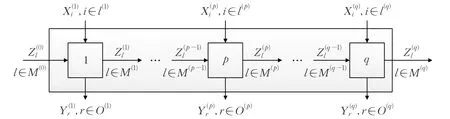
图1 串行网络模型

其中和分别为阶段1和阶段2模型的最优值。若=1并且所有的输入、输出松弛都为零，则称该DMU在阶段1是CCR有效的。若=1并且所有的输入、输出松弛都为零，则称该DMU在阶段2是CCR有效的。

独立两阶段模型简单易操作，在第一和第二阶段分别套用经典DEA方法，但是没有考虑两个阶段之间的联系。比如：存在中期措施不同时处理的情况，甚至允许在第一阶段（当被视为产出时）将其增加，并在第二阶段（当被视为投入时）将其减少，由此会引发冲突。此外，由于独立两阶段模型是分别评估总体效率和单阶段效率的，没有建立总体效率和单阶段效率之间的联系，因此DMU总体高效并不等价于单阶段也高效。

3.1.2 连接两阶段模型

为了克服独立两阶段模型的缺陷，连接两阶段DEA方法将阶段间相互作用纳入总体效率计算中，允许在两个阶段分别使用不同的乘数集，以保证：DMU总体有效对应了两个阶段完全有效。由于乘数集不同，因此不能用单一线性规划一次性处理两阶段的效率[38]。假设一共有D个中间措施指标。连接两阶段模型如公式（4）所示。

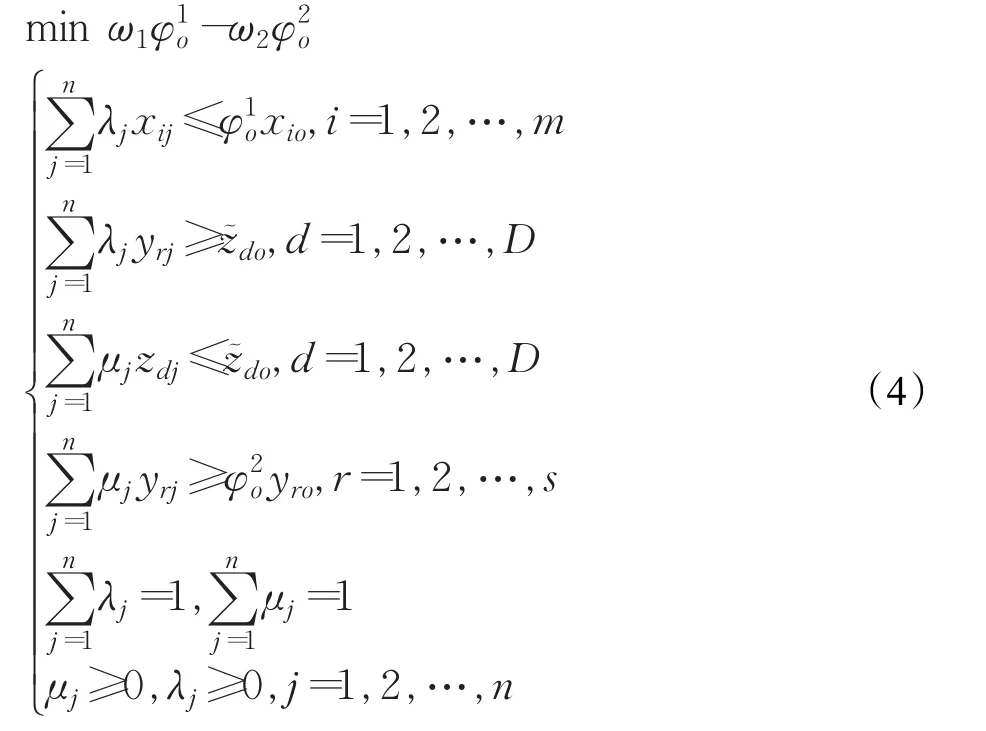
其中ω1和ω2是用户指定的权重，用于刻画用户对两个阶段表现的偏好，符号“～”表示未知的决策变量。模型中将中间措施视为未知的决策变量，有效定义了两阶段生产过程的有效前沿[38]。

网络模型按照结构不同分为串行结构、并行结构[39]和混合结构。串行网络模型最明显的特征是DMU之间存在较强的时间依赖关系，只有当前一个DMU产生中间措施后，后一个DMU才能开始工作。含有q个DMU的串行网络结构如图1所示。

根据不同应用场合的需要，串行网络模型可以在内部程序数量（一般形式有两个以上的阶段）、投入开始进行的阶段、产生输出的阶段[39]、中间的措施是否完全消耗等方面改进。模型具体计算由公式（5）给出。网络模型要求：相同的因子具有相同的乘数，与所在过程无关。

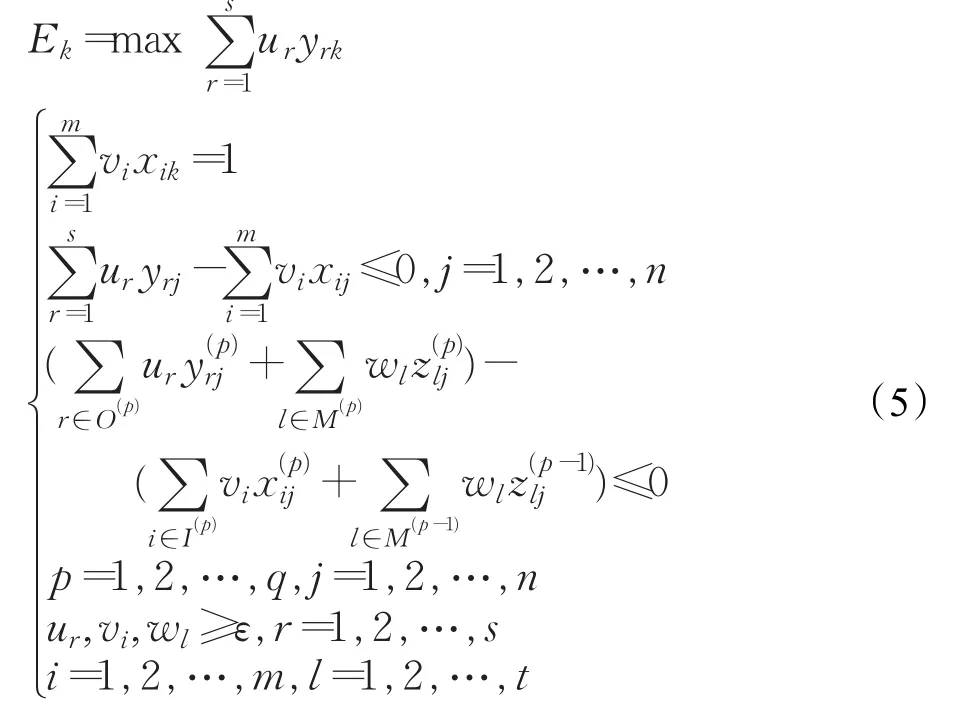
并行网络模型典型特征是各个级别彼此平行且分开地进行操作，DMU之间互相独立且不依赖。含有q个DMU的并行网络结构如图2所示。

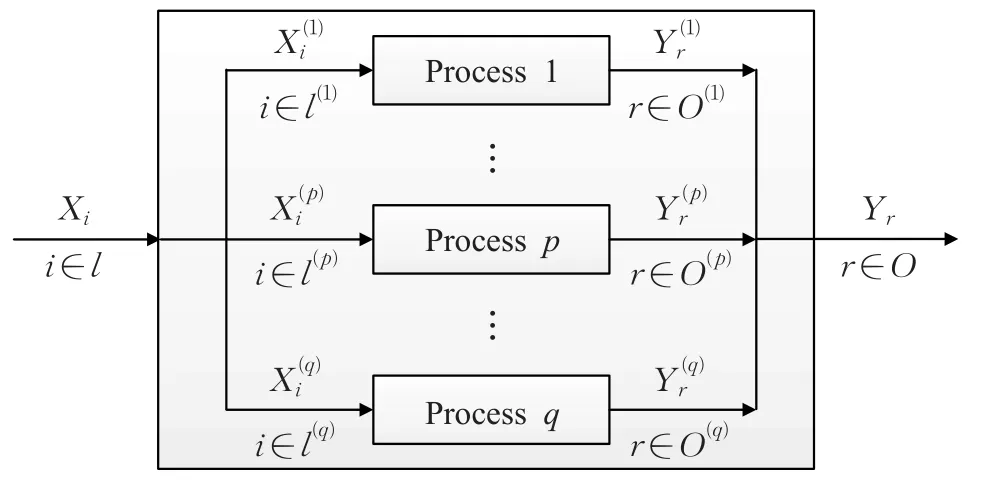
图2 并行网络结构

模型由公式（6）刻画。并行系统的典型示例是有部门的大学[39]。整个大学的效率通过所有部门的总投入和总产出计算。

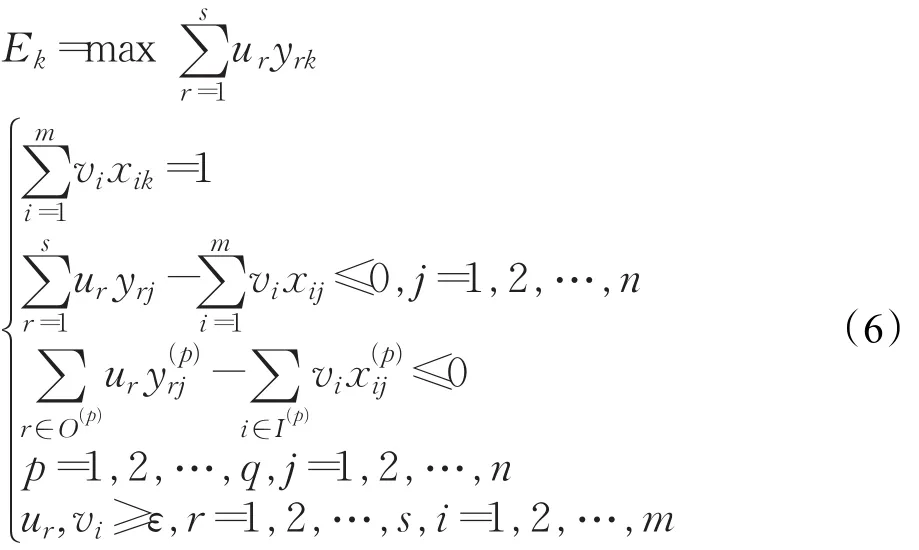
由于现实生活经验应用通常无法用单纯的串行结构或并行结构表示，因此提出采用将两者结合的方式构造混合网络结构[40-44]。通常，混合结构针对不同的经验应用有不同的构造。

3.1.3 关系两阶段模型

关系两阶段模型在充分考虑阶段之间相互影响的基础上，假定模型整体效率和单阶段效率存在一定的数学关系。关系两阶段模型与网络模型一样，要求中间措施必须在相关联的两个阶段中使用相同的乘数集合。

乘法模型的效率分解[45]如公式（7）所示。其中，Eo、、分别表示决策单元的总体效率和第一、二阶段的效率，、v、表示最优权重。乘法模型假设：总体效率是两个阶段的效率相乘，即Eo=×。

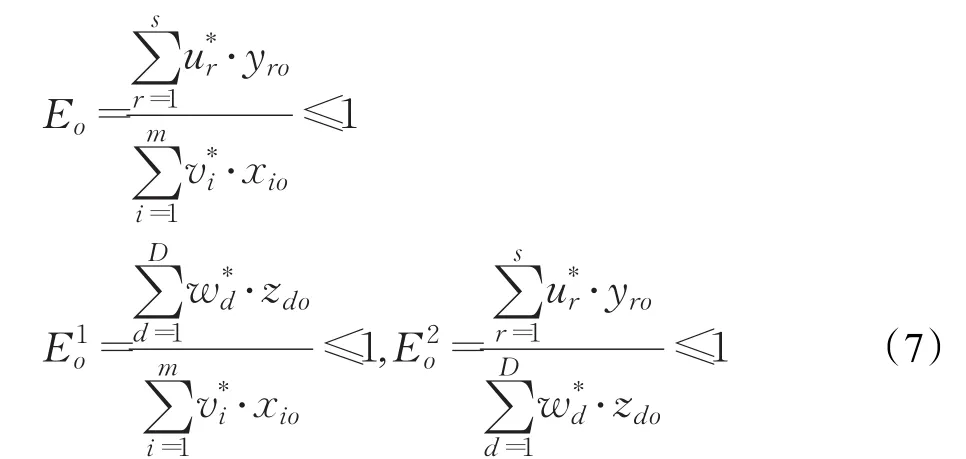
乘法模型评估效率分为两个步骤：第一步以总体效率最优为目标建立规划模型。第二步如公式（8）所示，要求模型在保持最优总体效率不变的前提下，以其中一个阶段（例如阶段二）的效率最大化为目标，这是为了解决第一步求解中，存在最优权重不唯一的情况。

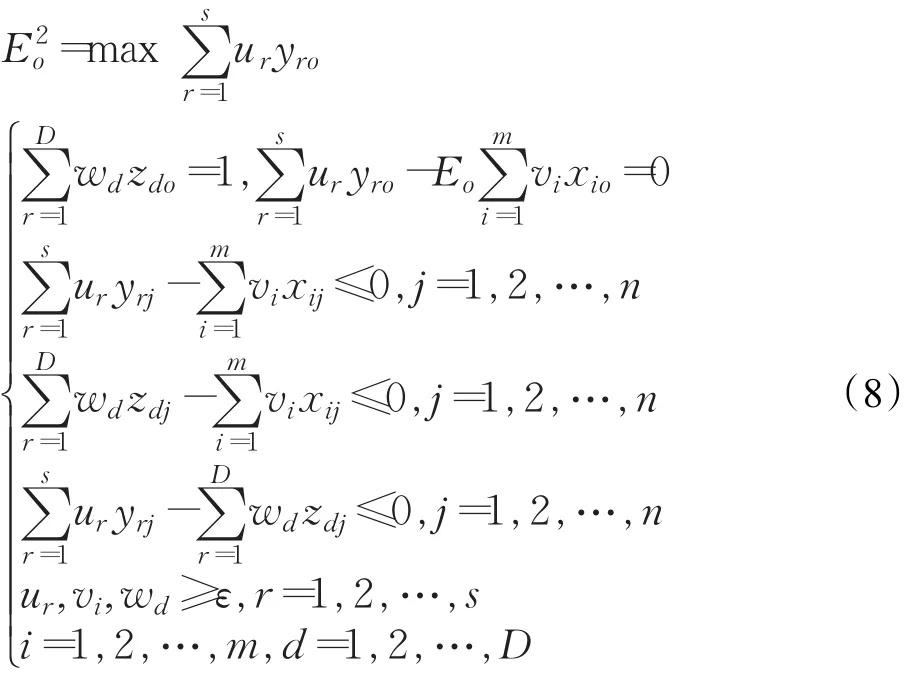
加法模型与乘法模型相同，同样分为两个步骤求解，差异主要体现在效率分解式上。加权求和[46]的分解方法按照公式（9）分解总体效率。其中，ξ1和ξ2分别表示两个阶段的权重系数，并且满足ξ1+ξ2=1。

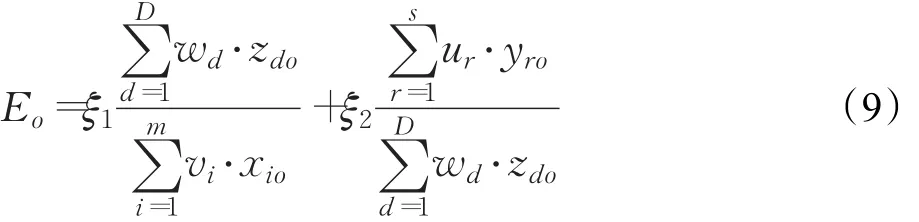
3.2 效率排序DEA模型

效率排序DEA的提出是为了解决经典DEA模型无法区分强大而不同的决策单元的问题。经典DEA只能根据效率得分是否为1将所有决策单元分为有效和非有效两组，无法为决策者宏观把握所有DMU提供更多信息。效率排序DEA通过对效率值为1的决策单元再区分，提供所有的决策单元在排名的相对次序，而不是简单的分组情况。

交叉效率排序法最早由Sexton等人[49]提出，由此开创了效率排序DEA的研究领域。Jahanshahloo G.R[50]等人根据与理想解决方案TOPSIS的相似性改进方法，使用订单偏好的技术计算最终效率得分。

超效率排序法由Andersen和Petersen[51]提出，该方法逐渐演变成用于异常值检测上[52]。Mehrabian等人开发的MAJ模型[53]克服了不可行性问题，同时解决了原模型对数据变化的敏感性问题。但是，大量模拟实验[54]已经证明，超高效率方法在评估决策单元的效率分数方面效果不理想。

Torgersen等人[55]提出了基准排序法，决策者根据决策单元重要程度对有效单位排序。另一种基准排序法的思路是根据有效DMU被用作低效DMU基准的频率对有效DMU排序[56]。Jahanshahloo G.R[57]等通过移除有效DMU改变参考数据集，按照有效DMU对边界线和低效单元的影响大小排序。

Friedman和Sinuany-Stern[58]借助相关分析（CCA），将每个DMU通过DEA实现的权重向量，拟合成由CCA确定的一组权重，给出了公共权重法的思想。一种后期分析方法[59]只使用平衡指数作为排序的依据。Wu等[60]改进后期分析法的模型，并使用最大平衡指数替代原来的平衡指数。

3.2.1 交叉效率排序法

交叉效率排序法使用n个线性规划评估（即传统DEA模型）的最优权重，为每个DMU的效率得分计算n次。所有DEA交叉效率分数的结果可以总结在交叉效率矩阵中，令hkj是交叉效率矩阵中第k行第 j列元素，如公式（10）所示，表示以第k个决策单元为评估对象时，第 j个决策单元的效率值，则矩阵中对角线上的元素hkk就是第k个DMU的传统DEA效率值。

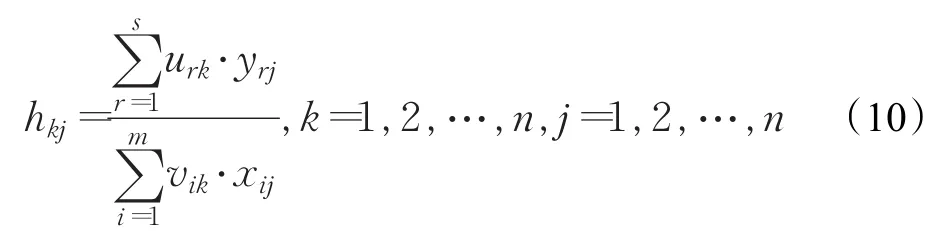
Sexton[49]通过计算平均交叉效率得分为所有决策单元按照效率值排序。Doyle和Green[61]基于该思想，提出了结合同行评估和自我评估的指标。基于交叉排序矩阵[62]的方法可以直接获得所有DMU的排序顺序。交叉效率方法避免了自我评估中存在的偏见，被认为是最可靠的排名方法之一。

3.2.2 超效率排序法

超效率排序法通过去除原始公式中的第k个约束，使有效的DMUk能够达到大于1的效率分数，如公式（11）所示。其中，J表示除去DMUk以外，其余DMU的集合。超效率模型实质是测量有效单位与排除之后的边界之间的距离，因此最有效的单位可以减少其产出而不降低其效率[52]。

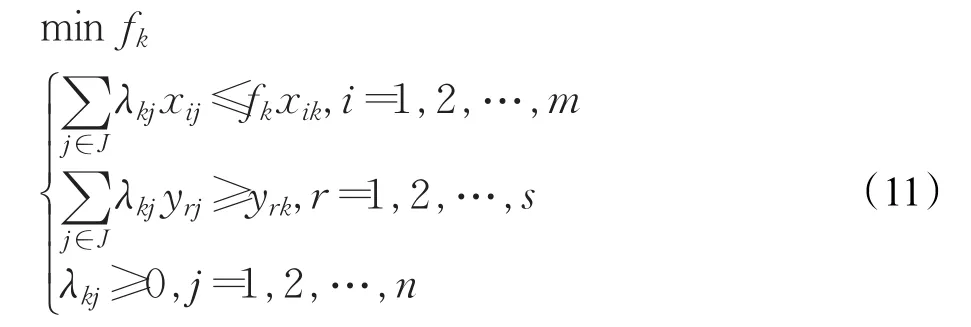
在实际应用中，超效率模型一方面存在造成部分单位达到非常高分数的缺陷，Sueyoshi[63]通过引入权重的具体界限解决了该问题。超效率模型的另一个缺点是其倾向于返回不可行的结果，不能为所有DMU提供完整排名。Thrall[64]以及Seiford和Zhu[65]讨论并证明超效率DEA模型的不可行条件。尽管MAJ模型解决了不可行性问题，但是由于超效率排序法结果的不理想，最新文献里已经很少提及该方法。

3.2.3 基准排序法

基准排序法评估的是有效单元相对于无效单元的重要性。该方法首先借助加法模型[66]确定所有松弛值为零的有效单元的集合V，再为每个决策单元计算径向度量，模型由公式（12）给出，径向度量E2i表示：当保持相同数量的输入时，最大输出的比率[52]。

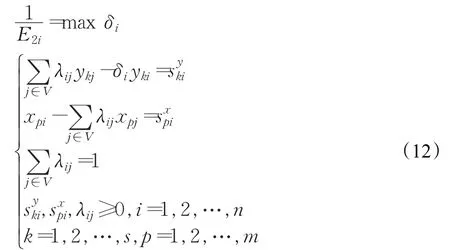
3.2.4 公共权重法

公共权重法旨在寻找传统统计方法与DEA的结合，使用共同权重对DMU进行多变量统计分析，进而对DMU排序。结合CCA方法，Friedman[58]等定义了一个新的缩放比T。其中Wj、Zj分别是输出、输入的线性组合。结合特征分析获取最大特征值对应的公共权重，并直接应用于DEA结果。

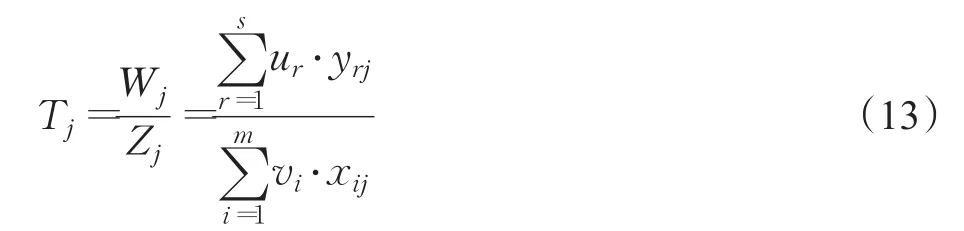
Wang等人[67]从模型应用的角度出发，指出大多数现有方法太复杂，难以应用甚至不可行，并提出基于回归分析的新方法，通过计算每个DMU最有利的权重最小化目标效率和实际DEA效率的差，为DMU效率排序寻求一组公共权重。

效率排序DEA很大程度上取决于决策者的投入，不存在适用于所有DEA排序问题的方法，决策者应该谨慎选择。

3.3 随机DEA模型

随机DEA是指基于统计公理或分布假设的非参数凸包参考技术的效率分析[68]。经典DEA模型默认所有的投入和产出无噪声，提供的是确定性前沿边界，随机DEA[68-76]把测量误差、样本噪声和规范误差等作为模型的组成部分，假定生产前沿随机，促使模型可以在统计框架内处理适当的假设。

Thore[69]和Land等[70]提出将统计特性应用到DEA模型中，Cooper等[72]结合统计特性，建立了机会约束DEA（CCDEA）模型，并给出了随机有效性的定义。模型由公式（14）给出。其中Pr代表概率，xij、yrj为已知分布的随机变量，αj和βj为相应的阈值。

Cooper等[72]提供了DMU随机有效的必要条件和DMU非随机有效性的充分条件。多变量，非参数随机边界模型[75]实现了DEA在数据生成方面的随机性；基于内核的前沿估计器平滑处理边界[76]，实现了DEA在前沿边界的随机性。

3.4 其他扩展问题

3.4.1 窗口数据

窗口数据和时序数据均是针对多周期模型提出的，用于评估不同决策单元在连续的多个时间周期内的效率问题。研究多周期问题时，不同年份的效率边界可能转移[77]；因此，对不同年份的所有观察数据汇总评估得到的前沿基准无法适用于所有时间观察点，3到4个时间段的窗口宽度往往会在效率测量中产生信息性和稳定性的最佳平衡[77]。

Charnes等[22]采用窗口数据分析研究了美国空军保养单元不同时间点的效率情况，Sun[78]使用同样的方法研究了大型商业银行的管理绩效问题。对于窗口数据存在初、末期的数据与中期数据使用频率不一致的缺陷，Sueyoshi[79]提出了DMU单元逐步递增的方法。

3.4.2 时序数据

窗口数据和时序数据的不同在于：窗口数据分析侧重于评估不同时间段的效率前沿，而时序数据侧重于计算相邻两个时间周期的效率变化情况。Malmquist[80]生产力指数（MPI）是时序数据分析的主要工具。

Caves等人[81]通过前一个时期t的生产水平来计算后一个时期t+1的相对效率，依此衡量效率的变化。但这会与用t+1时期生产水平评估t时期相对效率的结果产生二义性，Färe等人[82]提出使用两种相对效率的几何平均值作为MPI解决差异问题。2004年，Färe等人[83]又将MPI定义为 Mj(0,t)=D/D，评估DMUj在0时期到t时期的效率变化。当超过两个时期的比较时，用所有时期的观察数据构建全局前沿，即使用全局MPI[84-85]，更适合比较所有时期的效率。

3.4.3 存在负向变量的模型

经典DEA模型隐含的偏好是：投入越少并且产出越多。然而在很多应用场景中，例如，电场的污染、银行的不良贷款等指标，为了与物理过程保持一致，这些指标只能视作“坏”输出，使得模型中存在了负向变量。

Seiford和Zhu[86]提出了“翻译”法，借助翻译向量vr=maix(yri)+1,r∈B将不良输出转正，即=+vr＞0,r∈B。在VRS假设中，这种转换提供了相同的有效前沿。Juan Du等[87]提出分两个步骤求解的思路，第一步只处理所有正向变量，求得初步最优解后，第二步只处理负向变量，结合不同的约束条件和最优化目标获得最终最优解。Liu等[88]通过重新定义生产可能集，对存在负向投入产出变量DEA模型提出了完备的理论框架。模型如公式（15）所示。其中(X,Y)=(XD,XU,YD,YU)分别对应正向、负向的输入和输出。

4 DEA方法的研究趋势

作为管理科学的一个研究领域，DEA相关的研究工作（包括方法与实践）正在持续不断增长，这将会进一步推动DEA模型的拓展和应用范围的扩大。在当下DEA研究不断更新、发展的背景下，还存在以下几方面有待进一步完善。

4.1 两阶段DEA的进一步挖掘

在当下，两阶段DEA模型仍然是许多学者研究的热点，一方面是两阶段DEA模型的构建，另一方面是两阶段DEA相关理论的延伸。在两阶段DEA模型构建上，已经有学者提出了基于游戏理论[89]的领导-追随者模型，该模型优先选取其中一个阶段作为领导者，并在实践中取得了较好的应用。另外有研究在模型中加入博弈的思想，将两个阶段视作相互博弈的局中人，分别构建了合作式以及非合作式的模型[90]。另一种思路：假设总的效率是两个阶段效率的某个函数表达式，而不再是简单的加性或乘性关系，即EO=f(,)。模型求解时，先后最大化第一阶段和第二阶段效率。公式（16）给出了在这种构设下，第二阶段的求解模型。

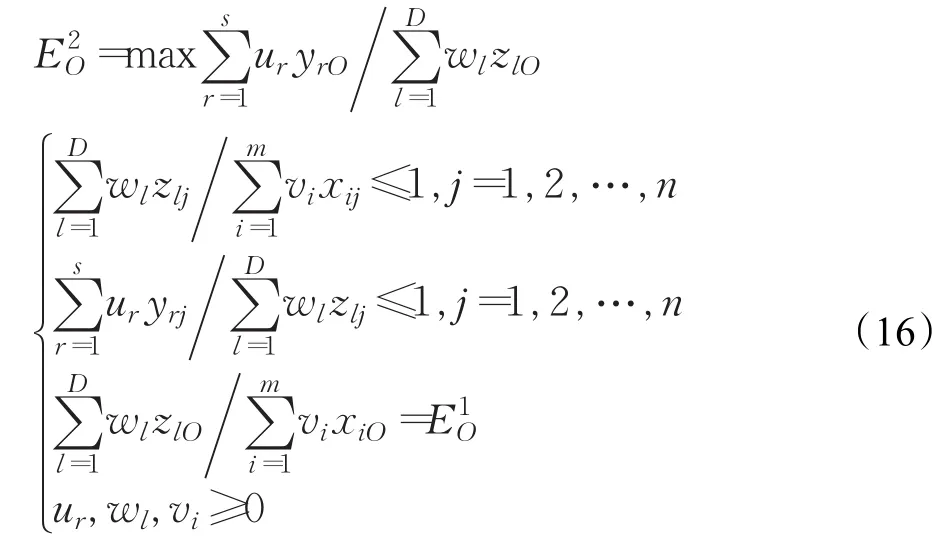
在两阶段DEA相关理论的延伸方面，目前应用较多的领导-追随者模型尚没有解决如何选取领导者的问题，在缺乏先验知识的情况下，如何选取领导者才能确保客观公平成为新的研究内容；Li等[89]指出，在中间措施的权重以及系统与其成员之间的协调方面，领导-追随者模型存在一定的外部性，得到的是有偏的求解结果，这种外部性可以通过增补或者抽取中间措施的操作解释。因此，领导-追随者模型需要进一步改进来消除所谓的“外部性”。

4.2 网络模型的深化

由于计算量大，解空间相对复杂，目前已有的关于网络模型的研究相对抽象，均是从宏观上泛化出相对简单的结构。如何对复杂网络系统进行建模和分析是需要进一步完善、解决的内容。结合启发式的搜索算法可以有效减少计算量，已经有学者开始尝试构建相对复杂的网络结构，借助启发式算法求解，为决策者提供DMU低效来源更精确的信息[91]。下一步可以进一步对网络结构拓展构设，打开黑箱，针对特定的某类问题来勾勒拓扑，以期和真实的物理过程保持一致，刻画更加复杂的网络结构，使得决策评估更精准。

4.3 DEA内外结合

内部结合是DEA不同模型之间的结合，例如Mohammad等人将两阶段DEA与随机DEA结合[92]，解决了存在不良数据情况下的两阶段效率评估问题。在前人的工作基础之上，还可以考虑网络DEA模型与时序数据的结合，即当网络结构是动态变化时，应该如何去描述、建立模型有待进一步研究，包括配置效率和规模收益情况等；再例如，尽管两阶段DEA通过打开黑箱放大了DMU的低效问题，但是同样存在着DMU之间效率不可比的可能性，两阶段DEA与指标绩效排序结合问题还不充分。

其次是DEA与其他综合评价方法的外部结合，使综合评价的结果更能符合客观实际。这方面最经典的案例就是将DEA与计量经济方法结合而成的DEA-Tobit模型。另外也有将DEA与基准测试结合，解决了相似背景不同群体的目标设定问题[93]。有学者将DEA与DE和MODE结合[94]，增加了DEA的“歧视力”，得到了更接进实际的结果。此外，在构建指标评价体系时，可以研究将随机DEA与AHP、PCA等方法结合。

4.4 DEA应用拓展

DEA应用扩展包括DEA在已有应用领域延展和在其他领域应用开发。

DEA在银行金融、能源效率、资源分配等多个交叉学科主题中均取得了满意的效果，但是还不够充分。除了评估已有数据外，还可以利用时序DEA[95]实现金融危机动态预测。目前关于资源分配的研究中，均假设存在中央决策单元完成集中式分配，通过同时投影所有DMU使总产出最大，尚没有研究将“非合作”决策者主观偏好纳入模型。假设每个DMU分别属于多个不同分组，分组满足组内合作、组间竞争的关系。在这种情况下，优化目标就转换成以各分组为单位，每个分组的总产出最大。当总的资源有限时，需要考虑不同分组应该怎样协调资源，如何通过DEA模型体现决策者的价值判断，是需要进一步研究的内容。

另外，将DEA方法应用到新的场景下，不断进行多学科、跨学科渗透，以及在不同领域建立绩效指标等。例如将网络DEA用于快递信使行业[96]。

4.5 其他方面

除以上列举的方面之外，DEA可供研究拓展的内容还可以包括：构建生产前沿时，只选取满足一定条件的DMU而不是全部DMU作为参考集[97]；将并行网络DEA模型应用到指标聚合问题中，即假定每个并行单元都是单输入单输出的特殊情况；在构建指标体系时应该如何选取指标，即对指标进行评估。随着大数据时代的到来，DEA运算效率如何适应大数据背景下的多目标决策也是需要考虑的问题。

5 结束语

本文在介绍DEA基本模型和思想的基础上，围绕近年来DEA研究的热点——两阶段DEA、效率排序DEA、随机DEA和其他相关扩展问题进行了梳理和分类，并预测了DEA未来可能的研究趋势。DEA模型理论的不断更新和发展，将会进一步推动DEA模型的研究热潮。

：

[1] 魏权龄.数据包络分析（DEA）[J].科学通报，2000，45（17）：1793-1808.

[2]杨国梁，刘文斌，郑海军.数据包络分析方法（DEA）综述[J].系统工程学报，2013，28（6）：840-860.

[3]朱乔.数据包络分析（DEA）方法综述与展望[J].系统管理学报，1994（4）：1-9.

[4]Farrell M J.The measurement of productive efficiency[J].Journal of the Royal Statistical Society，1957，120（3）：253-290.

[5]Charnes A，Cooper W W，Rhodes E.Measuring the efficiency of decision making units[J].European Journal of Operational Research，1978，2（6）：429-444.

[6]魏权龄.评价相对有效性的DEA方法[M].北京：中国人民大学出版社，1988.

[7]Kordrostami S，Amirteimoori A.Un-desirable factors in multi-component performance measurement[J].Applied Mathematics&Computation，2005，171（2）：721-729.

[8]Azadeh A，Amalnick M S，Ghaderi S F，et al.An integrated DEA PCA numerical taxonomy approach for energy efficiency assessment and consumption optimization in energy intensive manufacturing sectors[J].Energy Policy，2007，35（7）：3792-3806.

[9]Zhang B，Bi J，Fan Z，et al.Eco-efficiency analysis of industrial system in China：a data envelopment analysis approach[J].Ecological Economics，2008，68（1）：306-316.

[10]Tao Y，Zhang S.Environmental efficiency of electric power industry in the Yangtze River Delta[J].Mathematical&Computer Modelling，2013，58（5/6）：927-935.

[11]Zhou P，Sun Z R，Zhou D Q.Optimal path for controlling CO2，emissions in China：a perspective of efficiency analysis[J].Energy Economics，2014，45（C）：99-110.

[12]Chen X，Skully M，Brown K.Banking efficiency in China：application of DEA to pre-and post-deregulation eras：1993—2000[J].China Economic Review，2005，16（3）：229-245.

[13]Ariff M，Can L.Cost and profit efficiency of Chinese banks：a non-parametric analysis[J].China Economic Review，2008，19（2）：260-273.

[14]Fung M，Leung M.X-efficiency and convergence of productivity among the national commercial banks in China[C]//Proceedings of the 19th China Economic Association（UK）Annual Conference，University of Cam-bridge，UK，2008.

[15]Yao S，Han Z，Feng G.Ownership reform，foreign competition and efficiency of Chinese commercial banks：a non-parametric approach[J].World Economy，2008，31（10）：1310-1326.

[16]Laurenceson J，Qin F.Has minority foreign investment in China’s banks improved their cost efficiency?[J].China&World Economy，2008，16（3）：57-74.

[17]Golany B，Phillips F Y，Rousseau J J.Models for improved effectiveness based on DEA efficiency results[J].A I I E Transactions，1993，25（6）：2-10.

[18]Golany B，Tamir E.Evaluating efficiency-effectivenessequality trade-offs：a data envelopment analysis approach[J].Management Science，1995，41（7）：1172-1184.

[19]Zhang Y，Zhang H，Zhang R，et al.DEA-based production planning considering influencing factors[J].Journal of the Operational Research Society，2015，66（11）：1878-1886.

[20]Kumar C K，Sinha B K.Efficiency based production planning and control models[J].European Journal of Operational Research，1999，117（3）：450-469.

[21]Beasley J E.Allocating fixed costs and resources via data envelopment analysis[J].European Journal of Operational Research，2003，147（1）：198-216.

[22]Charnes A，Clark C T，Cooper W W，et al.A developmental study of data envelopment analysis in measuring the efficiency of maintenance units in the U.S.air forces[J].Annals of Operations Research，1984，2（1）：95-112.

[23]Roll Y，Golany B，Seroussy D.Measuring the efficiency of maintenance units in the Israeli Air Force[J].European Journal of Operational Research，1989，43（2）：136-142.

[24]Clarke R L.Evaluating USAF vehicle maintenance productivity over time：an application of data envelopment analysis[J].Decision Sciences，1992，23（2）：376-384.

[25]Bowlin W F.Financial analysis of civil reserve air fleet participants using data envelopment analysis[J].European Journal of Operational Research，2007，154（3）：691-709.

[26]Brockett P L，Cooper W W，Kumbhakar S C，et al.Alternative statistical regression studies of the effects of joint and service specific advertising on military recruitment[J].Journal of the Operational Research Society，2004，55（10）：1039-1048.

[27]Banker R D.Estimating most productive scale size using data envelopment analysis[J].European Journal of Operational Research，1984，17（1）：35-44.

[28]Cooper W W，Tone K，Seiford L M.Data envelopment analysis：acomprehensivetextwith models，applications references，and DEA-solver software with cdrom[M].[S.l.]：Kluwer Academic Publishers，1999.

[29]Charnes A，Cooper W W.Management models and industrialapplications oflinearprogramming[M].[S.l.]：Wiley，1961.

[30]Banker R D，Charnes A，Cooper W W.Some models for estimating technical and scale inefficiencies in data envelopment analysis[J].Management Science，1984，30（9）：1078-1092.

[31]Färe R，Grosskopf S，Lovell C A K.The measurement of efficiency of production[M].Netherlands：Springer，1985.

[32]Färe R，Grosskopf S，Lovell C A K.Production frontiers[M].[S.l.]：Cambridge University Press，1994.

[33]Yaakovrol L，Cook W，Boazgolan Y.Controlling factor weights in data envelopment analysis[J].A I I E Transactions，1991，23（1）：2-9.

[34]Tone K.A slacks-based measure of efficiency in data envelopment analysis[J].European Journal of Operational Research，2001，130（3）：498-509.

[35]Zhang D，Li X，Meng W，et al.Measuring the performance of nations at the Olympic Games using DEA models with different preferences[J].Journal of the Operational Research Society，2009，60（7）：983-990.

[36]Wang C H，Gopal R D，Zionts S.Use of data envelopment analysis in assessing information technology impact on firm performance[J].Annals of Operations Research，1997，73（1）：191-213.

[37]Seiford L M，Zhu J.Profitability and marketability of the Top 55 U.S.commercial banks[J].Management Science，1999，45（9）：1270-1288.

[38]Yao C，Zhu J.Measuring information technology’s indirect impact on firm performance[J].Information Technology&Management，2004，5（1/2）：9-22.

[39]Kao C，Hwang S N.Efficiency measurement for network systems：IT impact on firm performance[J].Decision Support Systems，2010，48（3）：437-446.

[40]Avkiran N K.Opening the black box of efficiency analysis：An illustration with UAE banks[J].Omega，2009，37（4）：930-941.

[41]Moreno P，Lozano S.A network DEA assessment of team efficiency in the NBA[J].Annals of Operations Research，2014，214（1）：99-124.

[42]Lin T Y，Chiu S H.Using independent component analysis and network DEA to improve bank performance evaluation[J].Economic Modelling，2013，32（2）：608-616.

[43]Tone K.Network DEA：a slacks-based measure approach[J].European Journal of Operational Research，2009，197（1）：243-252.

[44]Hsieh L F，Lin L H.A performance evaluation model for international tourist hotels in Taiwan—an application of the relational network DEA[J].International Journal of Hospitality Management，2010，29（1）：14-24.

[45]Kao C，Hwang S N.Efficiency decomposition in twostage data envelopment analysis：an application to nonlife insurance companies in Taiwan[J].European Journal of Operational Research，2008，185（1）：418-429.

[46]Chen Y，Cook W D，Li N，et al.Additive efficiency decomposition in two-stage DEA[J].European Journal of Operational Research，2009，196（3）：1170-1176.

[47]Wang Y M，Chin K S.Some alternative DEA models for two-stage process[J].Expert Systems with Applications，2010，37（12）：8799-8808.

[48]Wang K，Huang W，Wu J，et al.Efficiency measures of the Chinese commercial banking system using an additive two-stage DEA[J].Omega，2014，44（2）：5-20.

[49]Sexton T R，Silkman R H，Hogan A J.Data envelopment analysis：critique and extensions[J].New Directions for Evaluation，2010，1986（32）：73-105.

[50]Jahanshahloo G R，Khodabakhshi M，Lotfi F H，et al.A cross-efficiency model based on super-efficiency for ranking units through the TOPSIS approach and its extension to the interval case[J].Mathematical&Computer Modelling，2011，53（9）：1946-1955.

[51]Andersen，Petersen，Christian N.A procedure for ranking efficient units in data envelopment analysis[J].Management Science，1993，39（10）：1261-1264.

[52]Aldamak A M，Zolfaghari S.Review of efficiency ranking methods in data envelopment analysis[J].Measurement，2017.

[53]Mehrabian S，Alirezaee M R，Jahanshahloo G R.A complete efficiency ranking of decision making units in data envelopmentanalysis[J].ComputationalOptimization &Applications，1999，14（2）：261-266.

[54]Banker R D，Chang H.The super-efficiency procedure for outlier identification，not for ranking efficient units[J].European Journal of Operational Research，2006，175（2）：1311-1320.

[55]Torgersen A M，Førsund F R，Kittelsen S A C.Slackadjusted efficiency measures and ranking of efficient units[J].Journal of Productivity Analysis，1996，7（4）：379-398.

[56]Sinuany-Stern Z，Mehrez A，Barboy A.Academic departments efficiency via DEA[J].Computers&Operations Research，1994，21（5）：543-556.

[57]Jahanshahloo G R，Junior H V，Lotfi F H，et al.A new DEA ranking system based on changing the reference set[J].European Journal of Operational Research，2007，181（1）：331-337.

[58]Friedman L，Sinuany-Stern Z.Scaling units via the canonical correlation analysis in the DEA context[J].European Journal of Operational Research，1997，100（3）：629-637.

[59]Alirezaee M R，Afsharian M.A complete ranking of DMUsusing restrictionsin DEA models[J].Applied Mathematics&Computation，2007，189（2）：1550-1559.

[60]Wu J，Yang F，Liang L.A modified complete ranking of DMUs using restrictions in DEA models[J].Applied Mathematics&Computation，2010，217（2）：745-751.

[61]Doyle J，Green R.Efficiency and cross-efficiency in DEA：derivations，meanings and uses[J].Journal of the Operational Research Society，1994，45（5）：567-578.

[62]Angiz M Z，Mustafa A，Kamali M J.Cross-ranking of decision making units in data envelopment analysis[J].Applied Mathematical Modelling，2013，37（1/2）：398-405.

[63]Sueyoshi T.DEA non-parametric ranking test and index measurement：slack-adjusted DEA and an application to Japanese agriculture cooperatives[J].Omega，1999，27（3）：315-326.

[64]Thrall R M.Duality，classification and slacks in DEA[J].Annals of Operations Research，1997，66（1）：109-138.

[65]Seiford L M，Zhu J.Infeasibility of super-efficiency data envelopment analysis models[J].Infor Information Systems&Operational Research，1999，37（2）：174-187.

[66]Charnes A，Cooper W W，Golany B，et al.Foundations of data envelopment analysis for Pareto-Koopmans efficient empirical production functions[J].Journal of Econometrics，1985，30（1/2）：91-107.

[67]Wang Y M，Luo Y，Lan Y X.Common weights for fully ranking decision making units by regression analysis[J].Expert Systems with Applications An International Journal，2011，38（8）：9122-9128.

[68]Olesen O B，Petersen N C.Stochastic data envelopment analysis——a review[J].European Journal of Operational Research，2016，251（1）：2-21.

[69]Thore S.Chance-constrained activity analysis[J].European Journal of Operational Research，1987，30（3）：267-269.

[70]Land K C，Lovell C A K，Thore S.Productive efficiency under capitalism and state socialism：the chanceconstrained programming approach[J].Public Finance=Finances Publiques，1992，47（Supplement）：109-121.

[71]Land K C，Lovell C K，Thore S.Productive efficiency under capitalism and state socialism：an empirical inquiry using chance-constrained data envelopment analysis[J].Technological Forecasting&Social Change，1994，46（2）：139-152.

[72]Cooper W W，Huang Z，Lelas V，et al.Chance constrained programming formulations for stochastic characterizations of efficiency and dominance in DEA[J].Journal of Productivity Analysis，1998，9（1）：53-79.

[73]Tavana M，Shiraz R K，Hatami-Marbini A，et al.Chanceconstrained DEA modelswith random fuzzy inputs and outputs[J].Knowledge-Based Systems，2013，52（6）：32-52.

[74]Olesen O B，Petersen N C.Chance constrained efficiency evaluation[J].Management Science，1995，41（3）：442-457.

[75]Simar L，Wilson P W.Estimation and inference in twostage，semi-parametric models of production processes[J].Journal of Econometrics，2007，136（1）：31-64.

[76]Chen X，Swanson N R.Recent advances and future directions in causality，prediction，and specification analysis[M].New York：Springer，2013.

[77]Charnes A，Cooper W W，Lewin A Y，et al.Data envelopment analysis：theory，methodology，and application[J].Journal of the Operational Research Society，1997，48（3）：332-333.

[78]Sun D B.Evaluation of managerial performance in large commercial banks by data envelopment analysis[J].U.m.i，1988.

[79]Sueyoshi T.Comparisons and analyses of managerial efficiency and returns to scale of telecommunication enterprises by using DEA/WINDOW[J].Communications of the Operations Research Society of Japan，1992，37（5）：210-219.

[80]Malmquist S.Index numbers and indifference surfaces[J].Trabajos De Estadistica，1953，4（2）：209-242.

[81]Caves D W，Christensen L R，Diewert W E.The economic theory of index numbers and the measurement of input，output，and productivity[J].Econometrica，1982，50（6）：1393-1414.

[82]Färe R，Grosskopf S，Norris M.Productivity growth，technical progress，and efficiency change in industrialized countries：reply[J].American Economic Review，1994，84（5）：1040-1044.

[83]Färe R，Grosskopf S.Modeling undesirable factors in efficiency evaluation：comment[J].European Journal of Operational Research，2004，157（1）：242-245.

[84]Pastor J T，Lovell C A K.A global Malmquist productivity index[J].Economics Letters，2005，88（2）：266-271.

[85]Yang B，Zhang Y，Zhang H，et al.Factor-specific Malmquist productivity index based on common weights DEA[J].Operational Research，2015，16（1）：1-20.

[86]Seiford L M，Zhu J.A response to comments on modeling undesirable factors in efficiency evaluation[J].European Journal of Operational Research，2005，161（2）：579-581.

[87]Du Juan，Liang Liang，Chen Yao，et al.DEA-based production planning[J].Omega，2010，38（1/2）：105-112.

[88]Liu W B，Meng W，Li X X，et al.DEA models with undesirable inputs and outputs[J].Annals of Operations Research，2010，173（1）：177-194.

[89]Li X.A fair evaluation of certain stage in a two-stage structure：revisiting the typical two-stage DEA approaches[J].Omega，2016，68.

[90]Du Juan，Liang.A bargaining game model for measuring performance of two-stage network structures[J].European Journal of Operational Research，2011，210（2）：390-397.

[91]Ma J，Qi L，Deng L.Efficiency measurement and decomposition in hybrid two-stage DEA with additional inputs[J].Expert Systems with Applications，2017，79：348-357.

[92]Mohammad I，Reza F S.Assessing sustainability of supply chains by chance-constrained two-stage DEA model in the presence of undesirable factors[J].Computers and Operations Research，2017.

[93]Cook W D.Within-group common benchmarking using DEA[J].European Journal of Operational Research，2017，256：901-910.

[94]Jauhar S K.Integrating DEA with DE and MODE for sustainable supplier selection[J].Journal of Computational Science，2017，21：299-306.

[95]Li Zhiyong.Dynamic prediction of financial distress using Malmquist DEA[J].Expert Systems with Applications，2017，80：94-106.

[96]Chodakowska E.Network DEA models for evaluating couriers and messengers[J].Procedia Engineering，2017，182：106-111.

[97]Zhang H，Zhang Y，Zhang R.Dimension-specific efficiency measurement using data envelopment analysis[J].Mathematical Problems in Engineering，2014：1-9.