回归算法对软件缺陷个数预测模型性能的影响
2018-05-21付忠旺
付忠旺,肖 蓉,余 啸,谷 懿
(1.湖北大学 计算机与信息工程学院,武汉 430062; 2.软件工程国家重点实验室(武汉大学),武汉 430072;3.湖北省教育信息化工程技术研究中心,武汉 430062)
0 引言
软件缺陷预测指的是通过从历史软件数据中学习出缺陷预测的模型,然后对新的软件模块进行预测,预测其是否有缺陷。如果预测该软件模块有缺陷则对该软件模块分配更多的软件测试人员,这样可以合理地分配测试资源。研究者已经提出了很多软件缺陷预测的方法[1-3]:陈翔等[4]总结了国内外在该研究领域取得的主要成果,但这些研究者提出的软件缺陷预测方法都是基于分类模型,即预测软件模块是否有缺陷;文献[5-6]指出,如果采用回归方法预测一个软件模块存在多少个缺陷时,可以优先测试缺陷个数多的模块,这样能够更好地分配测试资源。
举例来说,假如一个软件公司开发了一个包含有100个软件模块的新项目。由于项目交付时间提前,测试人员有限,在项目交付之前只能测试20个软件模块。因此,测试人员首先基于软件仓库中的历史软件模块数据建立了一个软件缺陷预测模型或者软件缺陷个数预测模型;然后利用预测模型预测这100个软件模块是否有缺陷或有多少个缺陷。假设缺陷预测模型预测这100个软件模块中30个软件模块有缺陷,由于在项目交付之前测试人员只能测试20个软件模块,因此测试人员不清楚应该测试这30个被预测为有缺陷的软件模块中的哪20个软件模块;但如果根据软件缺陷个数预测模型的预测结果,测试人员能够基于这100个软件模块的缺陷个数的预测值对这100个软件模块进行降序排序,优先测试前20个软件模块,即优先具有更多缺陷的软件模块,因此,预测软件缺陷个数相比单纯的预测软件模块是否有缺陷更利于优化软件测试资源的分配[7]。
目前在软件缺陷个数预测方面已有大量研究。Rathore等[8]探究了决策树回归算法在本项目缺陷个数预测模型和跨项目缺陷个数预测模型的预测性能,实验结果表明在采用绝对误差和相对误差作为评估指标时,决策树回归算法有很好的预测性能。Wang等[9]提出了利用历史数据构造缺陷状态转换模型,然后利用马尔可夫链预测将来每种状态下的缺陷个数。Afzal等[10]提出了利用基因编程算法来预测缺陷个数。Rathore等[11]提出了利用遗传算法和决策树回归算法来预测给定软件系统的缺陷个数的方法,在PROMISE提供的开源数据集上的实验结果表明该方法有较好的预测性能。
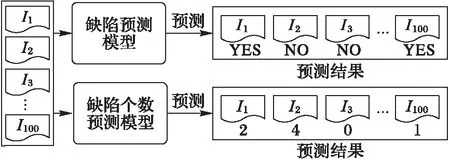
图1 缺陷预测模型与缺陷个数预测模型的差异性 Fig. 1 Difference between a defect prediction model and a model for predicting the number of defects
Gao等[12]比较了泊松回归算法、零膨胀泊松回归算法和负二项回归算法对于预测软件缺陷个数上的能力,实验采用平均绝对误差(Average Absolute Error, AAE)和平均相对误差(Average Relative Error, ARE)作为评价指标,实验结果表明泊松回归算法实现了最好的预测性能。Chen等[13]比较了线性回归算法、贝叶斯岭回归算法、支持向量机回归算法、最近邻回归算法、决策树回归算法和梯度Boosting回归算法的预测性能;实验采用均方回归误差和精度作为评价指标,实验结果表明在本项目缺陷个数预测和跨项目缺陷个数预测两种情形下,决策树回归算法都实现了最好的预测性能。在另一个比较相似的研究中,Rathore 等[14]基于PROMISE提供的开源数据集上比较了遗传算法、多层感知机回归算法、线性回归算法、决策树回归算法、零膨胀泊松回归算法和负二项回归算法等六种回归算法对于预测软件缺陷个数的能力;实验采用平均绝对误差和平均相对误差作为评价指标,实验结果表明线性回归算法和决策树回归算法对于大多数数据集而言产生的错误率最低并且相对于其他四种缺陷预测算法预测精准度更高。
但这些论文一般以评估回归模型的度量指标如均方根误差(Root Mean Square Error, RMSE)、平均绝对误差或平均相对误差来评价软件缺陷个数预测模型的预测性能。这些度量指标反映了预测值偏离真实值的程度,其值越小,表示预测准确率越高。如平均绝对误差的计算公式为:
其中:n为测试集中软件模块的个数,yi,predicted为测试集中第i个软件模块的缺陷个数预测值,yi,actual为测试集中第i个软件模块的缺陷个数真实值。
但是由于软件缺陷数据集是极度数据不平衡的,即大多数软件模块的缺陷个数为0,只有少数软件模块的缺陷个数大于0。仅用评价回归模型的度量指标评估软件缺陷个数预测模型性能的好坏是不合适的。以本文2.1节中Ant 1.3这个软件缺陷数据集为例,该数据集包含125个软件模块,其中20个软件模块是有缺陷的,总共有33个缺陷。假如一个预测模型在预测该数据集时预测这125个软件模块的缺陷个数均为0,AAE值为0.264(=33/125)。这个预测模型取得了很低的AAE,但是这样的预测模型不能应用到实际的应用场景中,因为它不能预测出任何有缺陷的软件模块的缺陷个数。
文献[5]指出,由于缺乏高质量的训练数据,准确地预测出一个模块包含几个缺陷是比较困难的。实际上,一般这些软件缺陷个数预测方法都是利用预测出的缺陷个数来对软件模块进行排序,优先测试包含更多缺陷的软件模块。因此Weyukers等[15]提出采用平均缺陷百分比(Fault Percentile Average, FPA)评价指标来评估软件缺陷个数预测模型的性能。
针对文献[12-14]在比较不同的回归算法对软件缺陷个数预测模型性能影响的研究中采用了均方根误差、平均绝对误差或平均相对误差等不合适的评价指标,有可能产生错误的结论的问题,本文提出了以平均缺陷百分比为评价指标,利用PROMISE提供的6个开源数据集,分析了线性回归、决策树回归、贝叶斯岭回归、自相关决策回归、支持向量回归、梯度Boosting回归、高斯过程回归、最近邻回归、随机梯度下降回归和Huber回归这10个常用的回归算法对软件缺陷个数预测模型预测结果的影响以及各种回归算法之间的差异。实验结果表明:梯度Boosting回归算法和贝叶斯岭回归算法预测效果最好。
本文主要工作为:
1)以平均缺陷百分比为评价指标分析了回归算法对软件缺陷个数预测模型预测性能的影响。
2)对比分析了10种常用的回归算法的差异,发现梯度Boosting回归算法和贝叶斯岭回归算法建立软件缺陷个数预测模型时具有最好的预测效果。
1 软件缺陷个数预测
1.1 软件缺陷个数预测流程
软件缺陷个数预测的流程如图1所示。第一步为从软件历史数据中提取出有用的软件模块,然后标记这些模块的特征和具有多少个缺陷。第二步为基于这些软件模块利用回归模型建立软件缺陷个数预测模型。第三步为对新的软件模块提取出特征,利用第二步中得到的软件缺陷个数预测模型预测这个新的软件模块的缺陷个数。
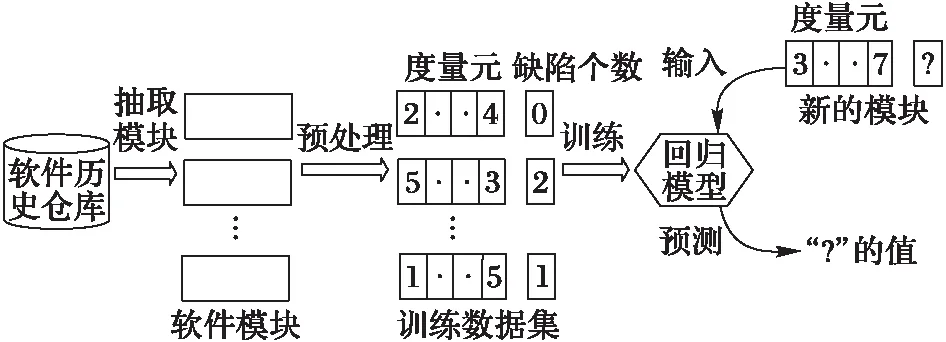
图2 软件缺陷个数预测流程 Fig. 2 Flow chart of predicting the number of software defects
1.2 回归算法
1.2.1 线性回归
线性回归(Linear Regression, LR)[16]是一种用于对因变量与一个或多个独立变量之间的线性关系进行建模的统计方法。一个线性回归方程为Y=b0+b1x1+b2x2+…+bnxn,其中:Y是因变量,x1,x2,…,xn是独立变量,b1,b2,…,bn是独立变量的回归系数,b0是误差项。针对软件缺陷个数预测模型,Y为缺陷个数,x1,x2,…,xn为软件模块的度量元。一般来说,线性回归都可以通过最小二乘法求出其方程。
1.2.2 决策树回归
决策树回归(Decision Tree Regression, DTR)[17]通过学习从数据特征推断的简单决策树来预测目标变量的值。决策树从根节点自上而下构建,并使用分割标准将数据分成包含具有相似值的实例的子集。选择最大化减少预期误差的属性作为根节点。该过程在非叶分支上递归运行,直到所有数据被处理。
1.2.3 贝叶斯岭回归
贝叶斯岭回归(Bayesian Ridge Regression, BRR)[18]假设先验概率、似然函数和后验概率都是正态分布。先验概率是假设模型输出Y是符合均值为Xθ的正态分布,正则化参数α被看作是一个需要从数据中估计得到的随机变量。回归系数θ的先验分布规律为球形正态分布,超参数为λ。贝叶斯岭回归通过最大化边际似然函数来估计超参数α和λ,以及回归系数θ。
1.2.4 自相关决策回归
自相关决策回归(Automatic Relevance Determination Regression, ARDR)[19]和贝叶斯岭回归很像,唯一的区别在于对回归系数θ的先验分布假设。自相关决策回归假设θ的先验分布规律为与坐标轴平行的椭圆形高斯分布。自相关决策回归也是通过最大化边际似然函数来估计超参数α和λ向量,以及回归系数θ。
1.2.5 支持向量回归
支持向量回归 (Support Vector Regression, SVR)[20]是支持向量在函数回归领域的应用。支持向量回归不同于支持向量机,支持向量回归的样本点只有一类,所寻求的最优超平面不是使两类样本点分得“最开”,而是使所有样本点离超平面的总偏差最小,这时样本点都在两条边界线之间。
1.2.6 梯度Boosting回归
梯度Boosting回归(Gradient Boosting Regression, GBR)[21]以弱预测模型(通常是决策树)的形式产生预测模型,类似于其他Boosting方法,都是以阶段性方式构建模型,但与其他Boosting方法不一样的是,梯度Boosting回归在迭代时选择的是梯度下降的方向来保证最后的结果最好。
1.2.7 高斯过程回归
高斯过程回归(Gaussian Process Regression, GPR)[22]与贝叶斯岭回归类似,区别在于高斯过程回归中用核函数代替了贝叶斯岭回归中的基函数。高斯过程回归从函数空间角度出发,定义一个高斯过程来描述函数分布,直接在函数空间进行贝叶斯推理。
1.2.8 最近邻回归
最近邻回归算法(Nearest Neighbors Regression, NNR)[23]通过找出一个样本的k个最近邻,将这k个最近邻的回归值的平均值赋给该样本,就可以得到该样本的回归值。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight),如权值与距离成正比。
1.2.9 随机梯度下降回归
随机梯度下降回归(Stochastic Gradient Descent Regression, SGDR)[24]是利用随机梯度下降的方法来最小化训练时回归方程中的误差的回归方法。
1.2.10 Huber回归
相比线性回归算法采用最小二乘法求出其回归方程,异常点对回归模型的影响会非常大,传统的基于最小二乘的回归方法将不适用。Huber回归 (Huber Regression, HR)[25]并不会忽略异常点,而是给予它们一个很小的权重值,因此对异常点具有鲁棒性。
2 实验设置
2.1 数据集
实验数据集为从PROMISE库中的6个常用的项目,这6个项目的详细信息如表1所示。对项目中的每个软件模块共提取了20个特征,这20个特征的具体细节参考文献[3]。
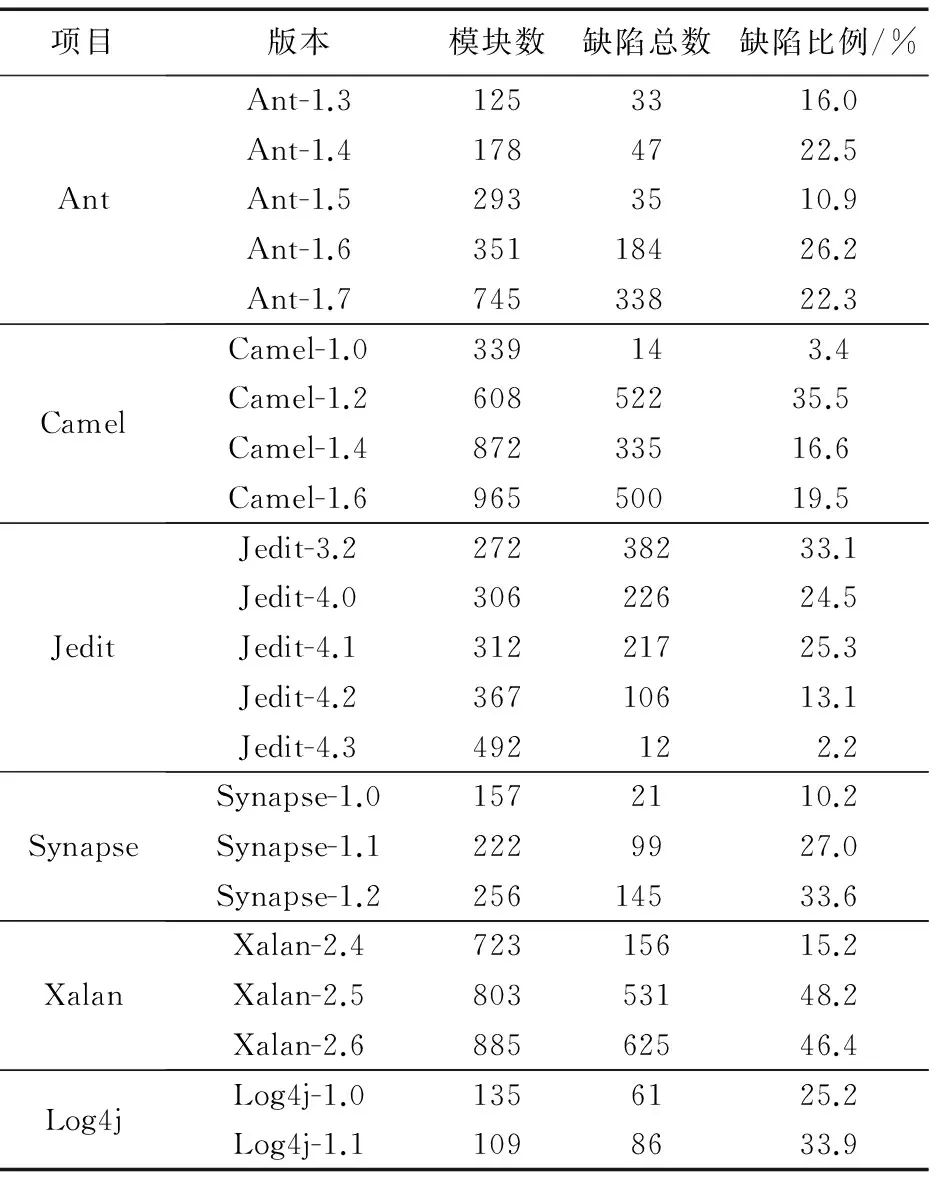
表1 实验数据集Tab. 1 Experimental data set
2.2 度量指标
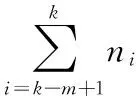
2.3 实验流程
为了评估1.2节中介绍的10个回归算法的预测性能,实验采用10折交叉检验方法。进行实验时,对于表1中的项目,是将该项目的所有版本合并为一个数据集。然后将该数据集均分为10份,轮流将其中的9份作训练集,1作做测试集,进行实验。每次实验在训练集上训练1.2节中介绍的10个回归算
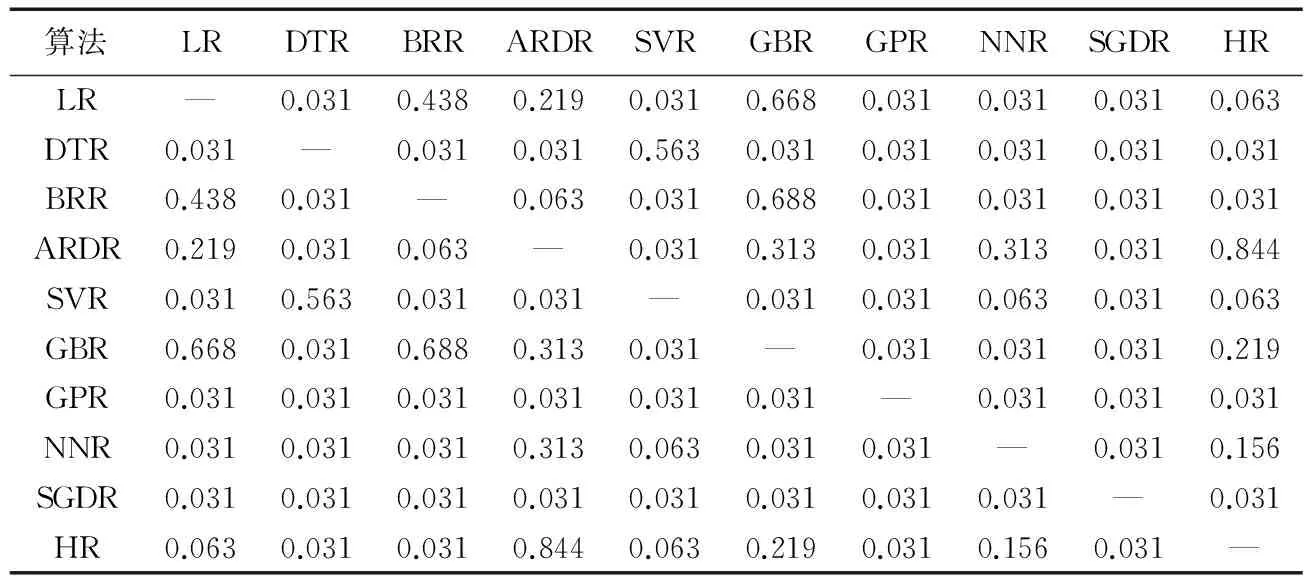
表2 预测结果的Wilcoxon符号秩检验(显著性水平0.05)Tab. 2 Wilcoxon symbol rank test of prediction results (significance level 0.05)
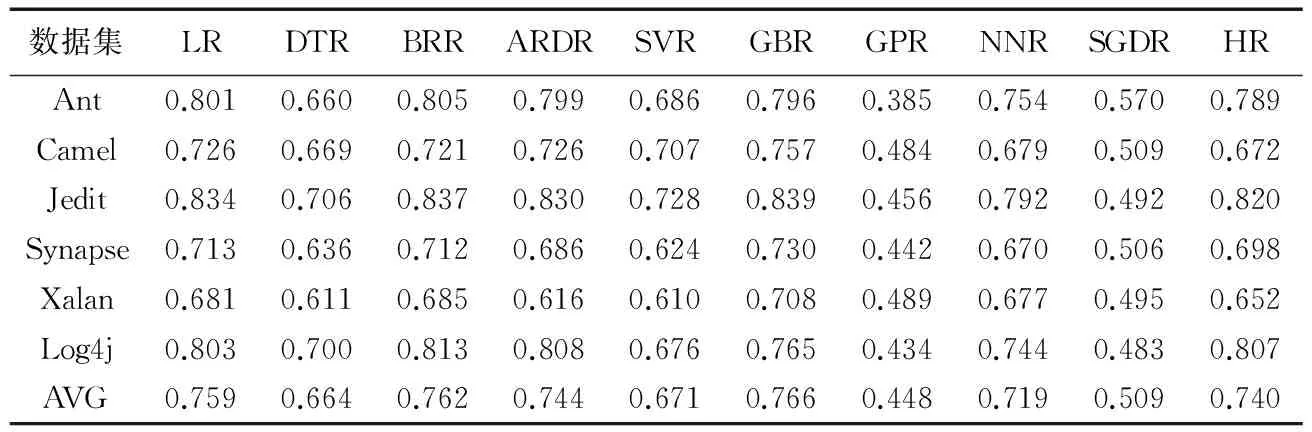
表3 每个项目预测结果统计Tab. 3 Statistics of each project’s prediction result
法,然后在测试集上测试这10个回归算法的FPA值。最后返回10次的结果的FPA值的平均值。为了防止样本误差,本实验进行20次10折交叉检验,最后记录的实验结果为20次10折交叉检验的FPA均值。
2.4 研究问题
本文提出了以下两个研究问题,为软件缺陷个数预测模型中各种回归算法的选择提供了指导依据。
RQ1:软件缺陷个数预测过程中,回归算法的选取是否影响预测效果?
RQ2:采用哪一个回归算法得到的软件缺陷个数预测模型的预测效果更好?
3 实验结果分析
3.1 针对RQ1
图3给出了10个回归算法在6个数据集上的预测结果的盒图,很容易看出预测结果分布有一定差别,其中LR、BRR、ARDR、GBR和HR这5种回归算法的效果较好FPA中位数分别为0.764、0.763、0.763、0.761和0.744,而效果较差的GPR和SGDR其中位数仅为0.449和0.501。BRR取得了最大的FPA值为0.813,GPR取得了最低的FPA值为0.385,BRR在6个数据集上取得的最低的FPA值都比GPR在这6个数据集上取得的最高的FPA值都要高。因此从图3的盒图可以看出,对RQ1的回答是肯定的,即在软件缺陷个数预测过程中,回归算法的选取会影响预测效果。
为了进一步分析这10个回归算法对预测效果的影响的显著程度,本文也对这10个回归算法的预测结果采用Wilcoxon符号秩检验进行了假设检验。在Wilcoxon符号秩检验中,它把观测值和零假设的中心位置之差的绝对值的秩分别按照不同的符号相加作为其检验统计量。它检验成对产生观测数据的总体是否具有相同的均值。本文建立原假设H0:两种回归算法预测结果来自同一分布,即它们之间没有差别。因此在显著性水平为0.05的情况下,若检测的显著性水平大于0.05,表示假设成立,接受H0;否则,假设不成立,拒绝H0。由表2可见,LR与除BRR、ARDR、GBR、HR外的算法显著性水平均小于0.05,说明LR与除BRR、ARDR、GBR、HR外的算法均有较大差异。DTR 与SVR的显著性水平为0.563,高于0.05,说明DTR与SVR没有较大差异,但与除了SVR外的算法显著性水平均小于0.05,说明DTR与除SVR外的算法有较大差异。BRR与除LR、ARDR、GBR外的算法显著性水平均小于0.05,说明BRR与除LR、ARDR、GBR外的算法具有较大差异。ARDR与DTR、SVR、GPR、SGDR外的算法显著性水平均小于0.05,说明ARDR与DTR、SVR、GPR、SGDR外的算法均有较大差异。SVR与除DTR、NNR、HR外的算法显著性水平均小于0.05,说明SVR与除DTR、NNR、HR外的算法具有较大差异。GBR与除LR、BRR、ARDR、HR外的算法显著性水平均小于0.05,说明GBR与除LR、BRR、ARDR、HR外的算法具有较大差异。NNR与除ARDR、SVR、HR外的算法显著性水平均小于0.05,说明NNR与除ARDR、SVR、HR外的算法具有较大差异。GPR和SGDR与所有除自身以外的其他算法的显著性水平均低于0.05,说明GPR和SGDR与其他算法都有较大差异。HR与LR、DTR、BRR、GPR、SGDR的显著性水平均小于0.05,说明HR与LR、DTR、BRR、GPR、SGDR都要较大差异。因此对第一个研究问题可以得出结论,回归算法的选取不仅对预测结果有影响,而且部分算法之间影响效果显著。
3.2 针对RQ2
从表2还可发现,LR、BRR、ARDR和GBR两两之间没有显著性差异,而HR和LR、ARDR、GBR、NNR之间也没有显著性差异。这是从6个数据集整体分析得到的结果,但在单个数据集上10种算法对预测结果的影响是否依然如此,还需作进一步分析。因此本文统计了在每个数据集上10种回归算法的预测结果。表3表明,在数据集Ant和Log4j中BRR占优且在Log4j这个数据集上取得FPA的最大值为0.813,而在数据集Camel、Jedit、Synapse和Xalan上GBR占优,取得的FPA的最大值为Jedit的0.839。在这6个数据集上,GBR取得最优的平均值为0.766,BRR取得第二好的平均值为0.762,但这两个平均值相差不大。因此对第二个研究问题可以得出结论,采用梯度Boosting回归算法和贝叶斯岭回归算法得到的软件缺陷个数预测模型的预测效果更好。
4 讨论
针对2.4节中提出的两个研究性问题,本文通过实验回答了这两个研究性问题,但实验过程中也潜在一些有效性威胁,具体如下:
1)实验选用的是PROMISE平台提供的6个数据集,虽然数据提供者Jureczko[26]曾表示这些数据在数据搜集过程中可能存在不足,但这6个数据集已经广泛地应用于软件缺陷个数预测的应用研究[8-13]中。因此,但本文坚信本文的实验结果具有一定的可信性和可重复性。
2)本文研究的10个回归算法均为较常见的回归算法,这些算法全部基于Sklearn包实现,算法参数使用Sklearn包中提供的默认参数,即本文没有对回归算法进行任何优化。
3)本文采用了平均缺陷百分比这个评价指标来评价软件缺陷个数预测模型的性能好坏,其他的一些指标如代价有效性图[27]也可以进行考虑。
5 结语
本文围绕软件缺陷个数预测展开研究,针对建立软件缺陷个数预测模型过程中回归算法的选择问题,分析了10个常见的回归算法对软件缺陷个数预测模型预测结果的影响以及各个回归算法之间的差异。研究结果表明:使用不同的回归算法建立的软件缺陷个数预测模型具有不同的预测效果,其中梯度Boosting回归算法和贝叶斯岭回归算法预测效果更好。
在后续的工作中,将进一步在更多的数据集上进行分析,验证本文得出的实验结果的一般性;此外,将理论上分析梯度Boosting回归算法和贝叶斯岭回归算法建立的缺陷数目预测模型预测效果较好的原因。
参考文献(References)
[1] RAHMAN R, POSNETT D, DEVANBU P. Recalling the “imprecision” of cross-project defect prediction [C]// FSE ’12: Proceedings of the ACM SIGSOFT 20th International Symposium on the Foundations of Software Engineering. New York: ACM, 2012: Article No. 61.
[2] SHEPPERD M, BOWES D, HALL T. Researcher bias: the use of machine learning in software defect prediction [J]. IEEE Transactions on Software Engineering, 2014, 40(6): 603-616.
[3] 王星,何鹏,陈丹,等.跨项目缺陷预测中训练数据选择方法[J].计算机应用,2016,36(11):3165-3169. (WANG X, HE P, CHEN D, et al. Selection of training data for cross-project defect prediction [J]. Journal of Computer Applications, 2016, 36(11): 3165-3169.)
[4] 陈翔,顾庆,刘望舒,等.静态软件缺陷预测方法研究[J].软件学报,2016,27(1):1-25. (CHEN X, GU Q, LIU W S, et al. Survey of static software defect prediction [J]. Journal of Software, 2016,27(1):1-25.)
[5] YANG X, TANG K, YAO X. A learning-to-rank approach to software defect prediction [J]. IEEE Transactions on Reliability, 2015, 64(1): 234-246.
[6] FENTON N E, NEIL M. A critique of software defect prediction models [J]. IEEE Transactions on Software Engineering, 1999, 25(5): 675-689.
[7] MALHOTRA R. A systematic review of machine learning techniques for software fault prediction [J]. Applied Soft Computing, 2015, 27: 504-518.
[8] RATHORE S S, KUMAR S. A decision tree regression based approach for the number of software faults prediction [J]. ACM Sigsoft Software Engineering Notes, 2016, 41(1): 1-6.
[9] WANG J, ZHANG H. Predicting defect numbers based on defect state transition models [C]// ESEM ’12: Proceedings of the 2012 ACM-IEEE International Symposium on Empirical Software Engineering and Measurement. New York: ACM, 2012: 191-200.
[10] AFZAL W, TORKAR R, FELDT R. Prediction of fault count data using genetic programming [C]// INMIC 2008: Proceedings of the 12th IEEE International Multitopic Conference. Piscataway, NJ: IEEE, 2008: 349-356.
[11] RATHORE S S, KUMAR S. Predicting number of faults in software system using genetic programming [J]. Procedia Computer Science, 2015, 62: 303-311.
[12] GAO K, KHOSHGOFTAAR T M. A comprehensive empirical study of count models for software fault prediction [J]. IEEE Transactions on Reliability, 2007, 56(2): 223-236.
[13] CHEN M, MA Y. An empirical study on predicting defect numbers [C]// Proceedings of the 27th International Conference on Software Engineering and Knowledge Engineering. Piscataway, NJ: IEEE, 2015:397-402.
[14] RATHORE S S, KUMAR S. An empirical study of some software fault prediction techniques for the number of faults prediction [J]. Soft Computing, 2016, 21(24): 7417-7434.
[15] WEYUKER E J, OSTRAND T J, BELL R M. Comparing the effectiveness of several modeling methods for fault prediction [J]. Empirical Software Engineering, 2010, 15(3): 277-295.
[16] ASAI H T S U K. Linear regression analysis with fuzzy model [J]. IEEE Transaction on System, Man and Cybernetics, 1982, 12(6): 903-907.
[17] XU M, WATANACHATURAPORN P, VARSHNEY P K, et al. Decision tree regression for soft classification of remote sensing data [J]. Remote Sensing of Environment, 2005, 97(3): 322-336.
[18] HOERL A E, KENNARD R W. Ridge regression: biased estimation for nonorthogonal problems [J]. Technometrics, 1970, 12(1): 55-67.
[19] JACOBS J P. Bayesian support vector regression with automatic relevance determination kernel for modeling of antenna input characteristics [J]. IEEE Transactions on Antennas and Propagation, 2012, 60(4): 2114-2118.
[20] BASAK D, PAL S, PATRANABIS D C. Support vector regression [J]. Neural Information Processing — Letters and Reviews, 2007, 11(10): 203-224.
[21] ELITH J, LEATHWICK J R, HASTIE T. A working guide to boosted regression trees [J]. Journal of Animal Ecology, 2008, 77(4): 802-813.
[23] ALTMAN N S. An introduction to kernel and nearest-neighbor nonparametric regression [J]. The American Statistician, 1992, 46(3): 175-185.
[24] CARPENTER B. Lazy sparse stochastic gradient descent for regularized multinomial logistic regression [R]. [S.l.]: Alias-i, Inc., 2008: 1-20.
[25] HUBER P J. Robust regression: asymptotics, conjectures and Monte Carlo [J]. The Annals of Statistics, 1973, 1(5): 799-821.
[26] JURECZKO M, MADEYSKI L. Towards identifying software project clusters with regard to defect prediction [C]// PROMISE ’10: Proceedings of the 6th International Conference on Predictive Models in Software Engineering. New York: ACM, 2010: Article No. 9.
[27] JIANG T, TAN L, KIM S. Personalized defect prediction automated software engineering [C]// ASE 2013: Proceedings of the IEEE/ACM 28th International Conference on Automated Software Engineering. Piscataway, NJ: IEEE, 2013: 279-289.
FUZhongwang, born in 1993, M. S. candidate. His research interests include data mining, software engineering.
XIAORong, born in 1980, Ph. D. candidate, lecturer. Her research interests include software engineering.
YUXiao, born in 1994, Ph. D. candidate. His research interests include software engineering, deep learning.
GUYi, born in 1996, undergraduate. His research interests include machine learning.
