电锅炉供热系统的供水温度控制研究与设计

刘智民 杜春梅 代长明 宋盼想

河北建筑工程学院 河北 张家口 075000

正文：

0 引言

供热系统由热源、管网及用户等组成，为了保证供暖质量，实现对供水温度的控制尤为重要。目前实际工程中的温度控制十分常见，而温度控制具有惯性和滞后性，对于存在滞后性的供热系统，其滞后性会给控制系统带来较大的影响，常见的控制方式难以满足要求，运用PID算法效果也欠佳。因此，本文提出一种控制方法，设计一种控制器实现对供水温度的控制，其原理为：在供水管道处安装温度变送器，检测供水温度，并将其采集到的信号反馈到控制器，经运算后再将控制信号传送给电磁调节阀，对阀门开度进行调节。该控制方法简单直接，使控制器在整个调控过程中带来的信息传输的时延性减小。

1 供热系统的温度控制原理

本文设计的供热系统采用质调节方式，该调节方式的优点是管路水力工况稳定，操作方便。电锅炉供热系统中供水温度控制原理如图1所示，被控对象是流入用户端的的供水温度，蓄热水箱流出的高温水与用户回水混合，通过电磁三通调节阀输出混水给用户供暖。在用户供水管道处安装温度变送器，将采集到的温度信号反馈到控制器，控制器将检测值与给定值进行比较计算后发出控制信息（控制指令），执行器接收到控制指令后对电磁三通阀进行调节。电磁三通阀开度由0至10分别表示最小开度与最大开度，开度越大供水温度越高，直至检测值与给定值相符为止。相应的，若检测到供水温度比给定温度值高，则调小阀门开度，直至检测值与给定值相符为止。

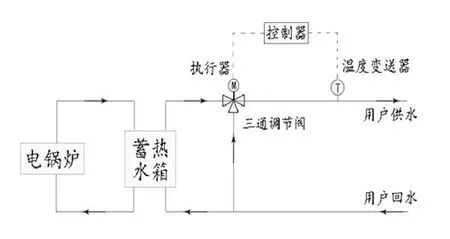
图1 供热系统供水温度控制原理图

在此供热控制系统中，不考虑管网的复杂性和难控性，假设管道热损耗为用户用热量的3%，根据热平衡关系建立简化的数学模型，如式（1）所示。

对式（1）两边进行拉氏变换，得

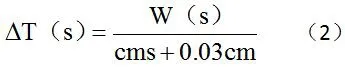
因为在实际工程中存在纯滞后环节，故数学模型应再串联一个纯滞后环节，滞后时间常数为，得

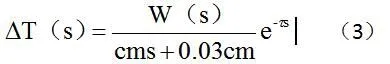
由式子（3）得供水温度控制系统的传递函数为式

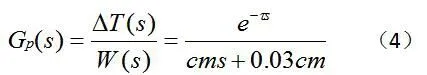
供水温度控制系统是一个带纯滞后环节的一阶惯性环节，输出量为供水温度，输入量为热源供给热量，可通过电磁三通调节阀控制。

2 供水温度控制的设计

大林算法是由美国IBM公司的大林（Dahllin）于1968年针对工业生产过程中含纯滞后的控制对象的控制算法，该算法的设计目标是将期望的闭环响应设计成一阶惯性加纯滞后，然后反过来得到能满足这种闭环响应的控制器。

图2 控制系统框图

在图2所示的控制系统中，Gc(z)为数字控制器，Gp(z)为控制对象，则闭环系统传递函数为

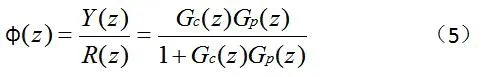
如果事先设定系统的闭环响应φ(s)，则可得控制器为

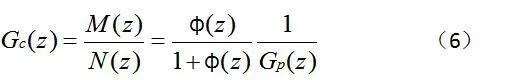
大林算法确定，期望的闭环响应是一阶惯性加纯滞后，纯滞后时间等于对象的纯滞后时间常数τ。

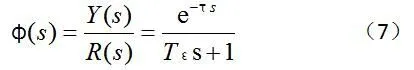
Z变换后得系统的闭环脉冲传递函数为

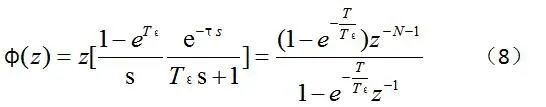
加入零阶保持器，将被控对象模型转换为

3 仿真结果

设供水温度控制系统的数据采样时间为0.06s，温度变送器安装点与执行器之间的管道l=6m，供水管道直径d=125mm，管道中水的流量u=39.5m3/h，管道中水的流速为0.95m/s，纯滞后时间的计算方法经计算得延时时间为6.7s左右，将TD=40，6.7

等参数代入上述相应公式中得到：

给定温度为45℃和50℃时，用Matlab仿真得到系统响应图分别为图3、4所示。

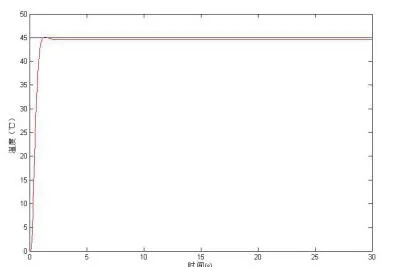
图3 给定温度45℃系统响应结果

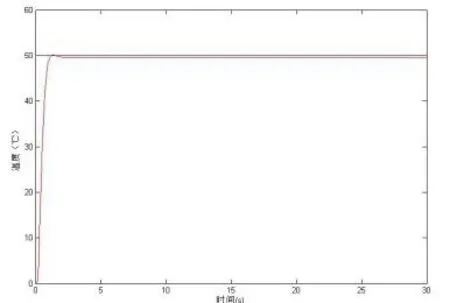
图4 给定温度50℃系统响应结果

图中纵坐标代表实际输出温度，横坐标代表响应时间。图中曲线显示：超调量很小，趋近于零，上升时间2S，稳态误差趋近于零，该温度控制系统能够快速跟踪给定值并且控制效果良好。仿真结果说明采用大林算法设计的供水温度控制系统超调量小，稳态误差小。大林算法是解决带有较大滞后控制系统的一种较理想的控制算法，本文采用大林算法编写的控制算法达到了控制供水温度的目的，具有一定的应用和推广价值。

4 总结

本文将大林算法应用于电锅炉供热系统模型之中来解决控制系统中纯滞后问题，运用Matlab软件对控制器算法进行仿真得到响应曲线。结果表明，此方法响应速度快，控制温度稳定，实现了减少超调量且控制迅速的目的，控制效果理想。