全天球太阳矢量确定算法及在速率阻尼中的应用

高海云 刘善伍 陈宏宇 王江秋 张学钢

上海微小卫星工程中心, 上海 201003

太阳矢量确定在航天工程中意义重大，直接关系到卫星的能源获取以及姿态确定等重要方面。通过对太阳辐射的敏感来测量太阳矢量的太阳敏感器，具有结构简单可靠性高、处理算法简单等诸多优点，在现代航天工程中应用广泛，并在太阳矢量的基础上研究设计了定姿、阻尼以及角速度估计等一系列相关算法[1-4]。

本文设计了一种全天球的太阳矢量确定算法，算法设计了集合多片太阳敏感器的敏感器组件，只需要在卫星表面对称位置安装2个敏感器组件就可以实现太阳矢量的全天球确定。这样既可以减少卫星表面敏感器的安装位置，简化敏感器与卫星表面设计的相互约束，还可以利用敏感器的特定几何结构，仅利用2片太阳敏感器就实现太阳矢量的确定。

在实现全天球太阳矢量确定的基础上，本文设计了一种卫星角速度估计和速率阻尼算法，与已有估计算法相比[5-12]，本文设计的算法仅利用太阳矢量信息就可以实现角速度的粗估计，利用估计得到的角速度信息进而实现卫星的速率阻尼，而且阻尼算法对于地磁矢量的测量精度鲁棒性高。角速度估计和阻尼算法简单，计算复杂度低，易于工程实现[13-15]。

1 敏感器组件设计

本文设计了一种敏感器组件来实现太阳矢量的全天球确定，结构如图1所示。组件由一个四棱台和5片余弦式太阳敏感器(#1～#5)组成，即对每片太阳敏感器，其输出信号强度I(电流)和太阳矢量sm之间满足

(1)

式中，ks是光电转化系数，n是敏感器单位法向矢量。

图1 敏感器组件结构示意图

为了实现全天球太阳矢量确定，需要在卫星的+Z和-Z方向上分别安装2个相同的敏感器组件，其安装矩阵分别为RbsA和RbsB。

2 全天球太阳矢量确定算法

针对图1所示的敏感器组件，除去太阳矢量平行和垂直与卫星Z轴时的特殊情况外，在任意时刻都可以保证：

1)至少有1个敏感器组件可以敏感到太阳光；

2)敏感到太阳光的组件仅存在2片或3片太阳敏感器可以敏感到太阳的情况，称为有效敏感器。

所以本文分别设计了使用2片和3片有效敏感器进行确定太阳矢量的算法。下面介绍利用敏感器组件确定太阳矢量的算法。

2.1 3片太阳敏感器确定太阳矢量的算法

由图1所示的敏感器组件结构可以确定，当有3片敏感器有效时，太阳敏感器#1必定有效。所以可以得到3片太阳敏感器有效时的太阳矢量确定算法

(2)

式中，nz，nj，nk和I1，Ij，Ik分别是太阳敏感器#1, #j和#k的法向单位矢量和输出信号强度，α，β和γ分别是太阳矢量与敏感器法向方向的夹角，j和k是有效太阳敏感器的编号，(j,k)∈{(2,3), (3,4), (4,5), (5,2)}，Sm是太阳矢量在敏感器组件坐标系中的表示。

其中，根据太阳电池片在五棱台的安装方式，计算可得到n1-5,5个法向单位矢量：

(3)

(4)

(5)

(6)

(7)

求解方程(2)，得到用3片太阳敏感器确定太阳矢量的计算公式

1)如果j=2,k=3:

(8)

2)如果j=3,k=4：

(9)

3)如果j=4,k=5：

(10)

4)如果j=5,k=2：

(11)

2.2 2片太阳敏感器确定太阳矢量的算法

2.2.1 太阳敏感器#1有效

当太阳敏感器#1有效时，则公式(2)可以简化为

(12)

式中，χ表示敏感器组件坐标系X轴或Y轴单位方向矢量nx和ny。求解方程(4)可以得到对应情况下的太阳矢量确定公式

1)如果j=2:

(13)

2)如果j=3：

(14)

3)如果j=4：

(15)

4)如果j=5：

(16)

2.2.2 太阳敏感器#1无效

如太阳敏感器#1无效，则方程(2)成为欠定方程，为了求解cosα，需要增加辅助条件太阳敏感器本体坐标系下的太阳矢量的模值等于1

(17)

式中，(j,k)={(2,3),(3,4),(4,5),(5,2)}，整理方程(17)得到含有cosα的一元二次方程

(18)

求解一元二次方程得到cosα的2个解

(19)

由于cosα表示太阳矢量与Z轴夹角余弦，因此cosα>0。而且此时Z轴方向的敏感器#1无效，所以cosα应当取结果中夹角较大的值，所以

(20)

综上，太阳矢量的确定公式与式(8)～(11)相同，式中cosα由公式(17)～(20)计算得到。

2.3 全天球太阳矢量确定算法

结合2.2节和2.3节的太阳矢量确定算法，下面介绍全天球太阳矢量确定算法。

1)对于敏感器组件A，判断太阳敏感器有效个数nA：

i.如果nA≥3，由式(2)～(11)计算smA；

ii.如果nA=2，由式(12)～(16)或式(17)～(20)、(2)～(11)计算smA；

iii.否则，置smA=0。

2)对于敏感器组件B，判断太阳敏感器有效个数nB：

i.如果nB≥3，由式(2)～(11)计算smB；

ii.如果nB=2，由式(12)～(16)或式(17)～(20)、(2)～(11)计算smB；

iii.否则，置smB=0。

3)综合敏感器组件A和B的信息，得到卫星本体坐标系下太阳矢量sb的计算公式

sb=RbsAsmA+RbsBsmB

全天球太阳矢量确定算法的流程图如图2所示。

图2 全天球太阳矢量确定算法流程

3 基于太阳矢量的阻尼算法

在实现全天球太阳矢量确定的基础上，本文设计了一种基于太阳矢量的阻尼算法，算法的基本思想是通过卫星本体坐标系下太阳矢量的变化情况计算得到卫星的角速度，进而实现角速度的阻尼。

根据矢量运算关系，可以得到

(21)

(22)

由方程(22)可得

(23)

(24)

所以，假设在卫星角速度不发生大的突变前提下，设如下方程

(25)

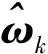
(26)

所以得到卫星的角速率阻尼算法：

(27)

式中，Kω是控制系数，ωd是期望的卫星角速度，sgn(·)表示符号函数，P0是磁力矩器的标称值。

分析式(26)和(27)所示的基于太阳矢量的阻尼算法，可以发现，算法主要依赖于太阳矢量的测量值，对于地磁矢量的测量精度要求很低，只需要保证地磁矢量测量值的三轴极性正确即可。在实际工程中，由于受到磁力矩器和其他电磁干扰的影响，高精度地磁矢量的测量值难以获得，而太阳矢量的测量所受干扰则很少。因此算法具有重要的工程实践指导意义。

将本文所提到的利用角速度估计和速率阻尼的算法同一般现有的阻尼算法进行对比[13-15]。在工程实际应用中的优势显而易见，首先，可以在卫星上使用低精度的商用磁强计。其次，在剩磁干扰过大的情况下依旧可以进行阻尼工作。

另外，本文的阻尼方式适用于在大角速率情况下进行阻尼，而现有的其他阻尼方式都无法更好地解决这个问题。根据本文叙述的阻尼方法，卫星在大角速率的情况下，如果在阴影区，便不进行阻尼工作。如果在光照区就利用太阳敏感器信息估计出角速度。同时利用磁强计的有效数据对卫星的磁控进行引导。而此时不一定需要精度非常高的磁强计进行定姿。这样，不但增加了在设计阶段的可选择性，而且可以更好降低成本。

4 仿真验证

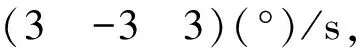
图3和图4为全天球太阳矢量确定算法的仿真结果。图3是算法确定的太阳矢量，图4是算法确定的太阳矢量与真实太阳矢量的误差夹角。图3和图4的仿真结果表明，无论卫星姿态如何变化，算法都可以唯一地确定出太阳矢量的方向，因此本文设计的太阳矢量确定算法可以实现太阳矢量的全天球确定，可以为基于太阳矢量的阻尼算法提供真实连续的太阳矢量变化信息。

图3 全天球捕获确定的太阳矢量

图4 全天球捕获的太阳矢量与真实太阳矢量的夹角

图5是基于太阳矢量的角速度阻尼仿真结果。从图中可以看出，即使初始角速度较大，阻尼算法也能有效完成阻尼。

图5 角速度阻尼仿真结果

5 结论

设计的太阳矢量确定算法利用特别设计的敏感器组件，能够在简化敏感器安装约束的前提下实现太阳矢量的全天球确定。利用可以在全天球确定得到的太阳矢量估计卫星的角速度,可以实现卫星的速率阻尼，而且阻尼算法对于难以提高测量精度的地磁矢量的敏感度低，算法结构简单，易于工程实现，具有重要的工程实践意义。

参 考 文 献

[1] Ruiter A H J D, Long T, Kumar B S, et al. Sun Vector-Based Attitude Determination of Passively Magnetically Stabilized Spacecraft[J]. Journal of Guidance Control & Dynamics, 2016:1-12.

[2] 刘善伍, 张锐, 谢祥华,等. 仅利用太阳矢量的卫星速率阻尼及太阳捕获控制新方法[J]. 自动化博览, 2011(S2):118-121. (Liu Shanwu, Zhang Rui, Xie Xianghua, et al. A New Controlling Method for Velocity Damping and Sun Acquisition of Satellite with Only Sun Vector[J]. Automation Panorama, 2011(S2):118-121.)

[3] 徐光延,廖培冲,张红梅. 基于太阳矢量和MEMS的自旋弹姿态估计系统研究[J]. 电光与控制,2016:1-8.(Xu Guangyan, Liao Peichong, Zhang Hongmei. Research on the Attitude Estimation System for Spinning Missile Based on the Sun Vector and MEMS[J]. Electronics Otics & Control, 2016:1-8.)

[4] Firoozi D, Namvar M. Noise Analysis in Satellite Attitude Estimation Using Angular Rate and a Single Vector Measurement[C], Decision and Control and European Control Conference. IEEE, 2011: 7476-7481.

[5] 马云建, 辛长范, 贾意弦, 等. 基于地磁传感器测量的滚转弹药角速度估计[J]. 弹箭与制导学报, 2016, 36(1):69-72.(Ma Yunjian, Xin Changfan, Jia Yixian, et al. Angular Velocity Estimation of Rolling-ammunition Based on Magnetometer[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2016, 36(1):69-72.)

[6] 单斌,梁勇奇,李恒年. 基于光度观测的空间目标姿态与角速度估计[J]. 光学学报, 2017,(05):144-155.(Shan Bin, Liang Yongqi, Li Hengnian. Attitude and Angular Speed Estimation of Spacial Objects Based on Photometric Observation[J]. Acta Optica Sinica, 2017,(05):144-155.)

[7] 杨杰,史震,岳鹏,程子健. 无陀螺惯性测量系统角速度估计算法[J]. 弹箭与制导学报, 2010,(03):25-28.(Yang Jie, Shi Zhen, Yue Peng, Cheng Zijian. Estimation Algorithm of Angular Velocity in Gyroscope-free Inertial Measurement System[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010,(03):25-28.)

[8] 郭朝礼,张笃周,王淑一. 欠驱动航天器滑模速率阻尼控制[J]. 空间控制技术与应用, 2013, (04):12-17.(Guo Chaoli, Zhang Duzhou, Wang Shuyi. Sliding Mode Control for Rate Damping of Underactuated Spacecraft[J]. Aerospace Control and Application, 2013(04):12-17.)

[9] 张利宾,杨旭,杨涤. 三轴稳定微小卫星主动磁阻尼姿态控制[J]. 上海航天,2008,(06):29-33. (Zhang Libin, Yang Xu, Yang Di. Active Magnetic Damping Attitude Control for Three Axis Stabilized Micro-Satellite[J]. Aerospace Shanghai, 2008,(06):29-33.)

[10] 党朝辉,项军华,刘昆. 仅有单个陀螺的Drag-free卫星初始速率阻尼模糊控制研究[J]. 上海航天,2012,(01):6-11.(Dang Zhaohui, Xiang Junhua, Liu Kun. A Fuzzy Control Method for Initial Angular Velocity Damping of Drag-Free Satellite Based on One Peg-Top[J]. Aerospace Shanghai, 2012(01):6-11.)

[11] 祁炜,鲁千红,罗玉文,单财良. 卫星初始速度阻尼智能控制器设计[J]. 计算机工程与应用,2011, 47(13):238-240,248.(Qi Wei, Lu Qianhong, Luo Yuwen, et al. Intelligent Controller for Damping of Satellite’s Initial Velocity[J]. Computer Engineering and Applications, 2011, 47(13): 238-240,248.)

[12] Coffey B. An Examination of Coarse Sun Sensor Contingencies in Attitude Determination and the Sun Vector Calculation[J]. 2012.

[13] 刘善伍, 陈宏宇, 张学钢. 卫星姿态四元数的连续化方法及姿态控制算法研究[J]. 航天控制, 2017,35(3):30-33.(Liu Shanwu, Chen Hongyu, Zhang Xuegang. The Algorithm of Continuous Quaternion and Attitude Control of Satellite[J]. Aerospace Control, 2017,35(3):30-33.)

[14] 谢祥华, 张锐, 张静. 基于磁强计与太阳敏感器的卫星自主定轨算法[J]. 宇航学报, 2009, 30(3):919-923.(Xie Xianghua, Zhang Rui, Zhang Jing. Satellite Autonomous Orbit Determination Based on Magnetometers and Sun Sensors[J]. Journal of Astronautics, 2009,30(3):919-923.)

[15] 刘海颖, 王惠南, 陈志明. 磁控微小卫星速率阻尼和姿态捕获研究[J]. 宇航学报, 2007, 28(2):333-337.(Liu Haiying, Wang Huinan, Chen Zhiming. Detunbling Controller and Attitudde Acquisition for Micro-satellite Based on Magnetic Torque[J]. Journal of Astronauntics, 2007, 28(2):333-337.)