基于输出反馈H∞控制的跟瞄平台稳定控制研究*

韩鹏娜 刘珊中 李 柯

河南科技大学信息工程学院，河南 471023

光电跟瞄平台广泛应用于飞机的火控系统、导航系统及精确的制导武器中，用以实现惯性空间稳定及目标跟踪双重功能。然而飞机在高速飞行中会受到振动、摩擦及各种不确定干扰的影响，致使探测装置抖动，容易丢失目标，命中率较低。因此，良好的稳定性是光电跟瞄平台稳定跟踪控制系统设计的先决条件。如何有效隔离环架的姿态扰动，减少探测装置抖动，是目前急需解决的问题。

近些年，国内外学者针对系统的稳定问题做了诸多研究。神经网络、自适应、状态反馈H∞控制和模糊控制等许多先进的控制方法被应用到稳定平台控制中，并取得一定成果[1-4]。其中，H∞控制是从根本上解决控制对象模型存在摄动及外界不确定性干扰问题的有效方法，适用于状态空间实现的多输入多输出(MIMO)场合，具有极好的鲁棒性[5]。文献[6-8]通过对黎卡提方程或线性矩阵不等式(LMI)求解，进而获得状态反馈H∞控制器，通过仿真结果验证，在外界存在振动、噪声等不确定性干扰且模型参数摄动时，均能体现良好的鲁棒性[9]。然而，实际系统的状态往往不能直接测量，无法直接采用状态反馈对系统进行控制，状态观测器的加入也会对系统的可靠性产生一定影响。输出反馈则不存在上述问题且较少使用，因此，在能达到闭环系统稳定性要求的前提下，输出反馈H∞控制不失为更好的探索方向。

本文以忽略环架间耦合所建立的数学模型为研究对象，通过对LMI求解，完成光电跟瞄平台输出反馈H∞稳定控制器设计。

1 光电跟瞄平台结构

光电跟瞄平台的环架结构如图1所示，由内到外依次为：方位、俯仰及横滚环[10]。其中，光电探测器固连于方位环，方位环与俯仰环、俯仰环与横滚环、横滚环与基座间分别通过方位轴、俯仰轴及横滚轴实现相对转动。力矩电机通过3个转轴将驱动力矩分别作用在各个环上，通过驱动各环转动，实现光电探测器对目标视线的全方位追踪。

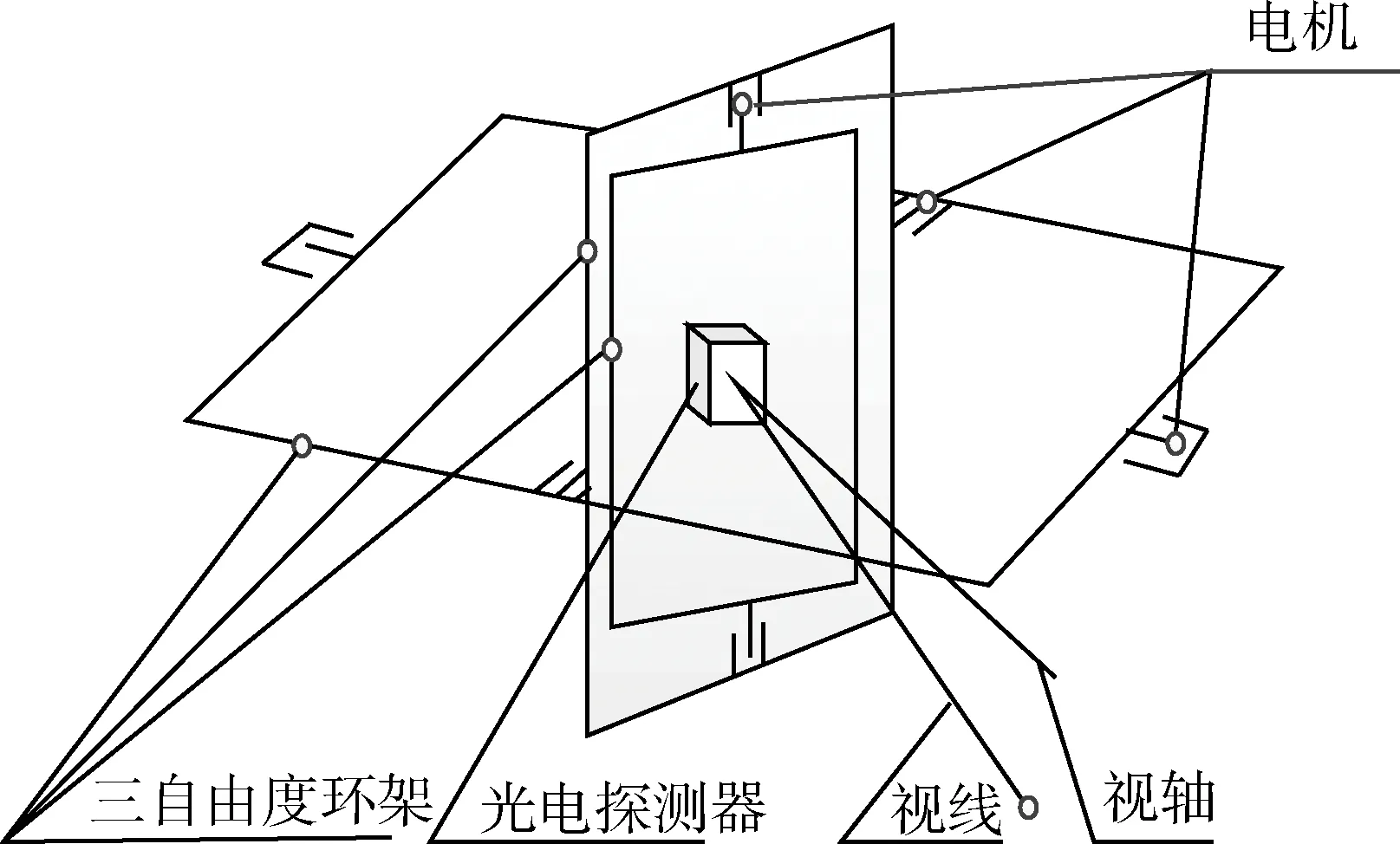
图1 跟瞄平台环架结构图

2 光电跟瞄平台稳定回路模型的建立

跟瞄平台稳定回路的工作原理如图2所示，由作为被控对象的平台环架，放大控制指令的功率放大器，输出驱动力矩的伺服电机及检测平台运动的位置陀螺构成。

图2 稳定回路工作原理图

对稳定回路的各组成部分，根据其工作原理进行分析研究，以方位环为例建立外界干扰作用下的环架运动状态空间模型。

2.1 平台框架

对于平台框架的机械结构，一般认为其结构谐振频率高于200Hz，在低频信号下视作刚体，依据刚体转动的牛顿定律存在：

(1)

J∑是电机转子、角度传感器转子(固连于平台)和平台框架自身的转动惯量之和；M∑由电机的输出转矩、基座角速度引起的力矩扰动和其他干扰力矩组成；ω为平台环架相对于惯性空间的角速度。

2.2 伺服力矩电机

采用无减速器直接驱动的力矩电机，是一种特殊的直流力矩电机，当初始条件为0时，电机回路方程为：

(2)

电机的输出转矩为：Mo(s)=Koia(s)，设ωi为基座干扰角速度，则伺服力矩电机的反电动势为：e(s)=Kε[ω(s)-ωi(s)]，

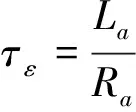
2.3 功率放大器

采用PWM方式进行功率放大，一般可视为比例环节。

2.4 位置陀螺仪

位置陀螺又称积分速率陀螺，采用速率陀螺仪的稳定平台响应速度较快，采用位置陀螺仪则利于提高稳定平台精度。为提高系统稳定跟踪的精度，采用位置陀螺仪，其传递函数为：

(3)

式中τg是时间常数；Km是比例因子(Km=KpKa)。陀螺的输入为指令角速度ωa与框架相对于惯性空间的角速度ω之间的差值，输出为偏差角度。

将对系统参数产生影响的干扰力矩及扰动角速度考虑进模型参数摄动中，并结合稳定回路各部分数学模型，得到环架运动的状态空间模型为：

(4)

其中：

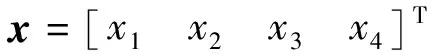
3 输出反馈H∞控制器设计

3.1 基于LMI的输出反馈H∞控制理论

定义性能评价指标：

z=C1x+D11w+D12u

(5)

得到方位环的增广被控对象的状态空间模型为：

(6)

其中，u为控制输入，w为干扰信号，我们设定干扰是不确定的，但具有有限能量，即w∈L2。

设定如下指标：

1)(A，B2)可稳定，(C2，A)可检测；

2)D11=D22=0。

要设计一个如式(7)所示状态空间实现的输出反馈H∞控制器u=K(s)y(s)。

(7)

(8)

其中：

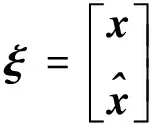
Dc1=D11+D12DkD21

(9)

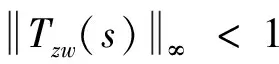
(10)

3.2 基于LMI的输出反馈H∞控制器设计

结合3.1节给出的输出反馈H∞控制器存在条件，通过如下步骤完成控制器的设计。

1)定义干扰抑制性能指标，选取适当的参数，确立控制对象模型，令：

得系统矩阵：

3)将Ak，Bk，Ck，Dk代入式(9)解出Ac1，Bc1，Cc1，Dc1，代入不等式(10)验证Xc1是否是对称正定阵，若满足则所得出的即是要求的控制器。若不满足条件则调整C1，D12，D21矩阵里的参数，重复以上步骤。

4 仿真研究

以方位环为例，取q1=q2=q3=q4=0.01，r1=1，r2=0.1时计算γ=0.1的次优H∞控制器为：

俯仰环与横滚环的输出反馈H∞稳定控制器的设计方法与上述类似，不再赘述。根据设计的控制器，完成闭环稳定回路模型搭建，对该系统在不确定干扰作用下分模型摄动与不摄动2种情况进行仿真研究，结果如下。

4.1 模型参数不摄动

1)指令角速度ωa=0rad/s，在方位、俯仰及横滚环架上分别加入wi=Mf的阶跃扰动信号，幅值分别为：0.2，0.2，0.5，其仿真结果如图3所示。

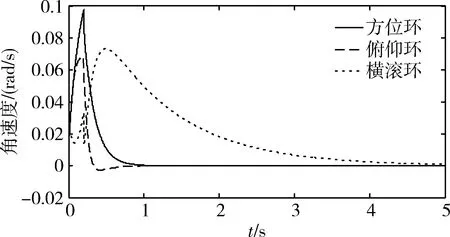
图3 同时作用扰动力矩与基座扰动角速度仿真结果

2)输入指令角速度ωa=0rad/s，在方位、俯仰及横滚环架上分别加入wi=Mf的阶跃扰动信号，幅值分别为：0.2，0.2，0.5。同时将频率从20Hz～60Hz随机变化的基座角振动扰动分别作用在三环架上，其仿真结果如图4所示。

图4 各种扰动同时作用下仿真结果

3)输入指令角速度ωa=0.8rad/s，作用的扰动信号同上述(2)，可得如图5所示的仿真结果。

图5 控制输入与扰动同时作用下仿真结果

4.2 模型参数摄动

一般情况下，伺服力矩电机的电磁时间常数上下存在10%的摄动，作用如上述(2)相同的外界干扰，并分别在方位、俯仰及横滚电机上加入参数摄动，其仿真结果如图6～7所示：

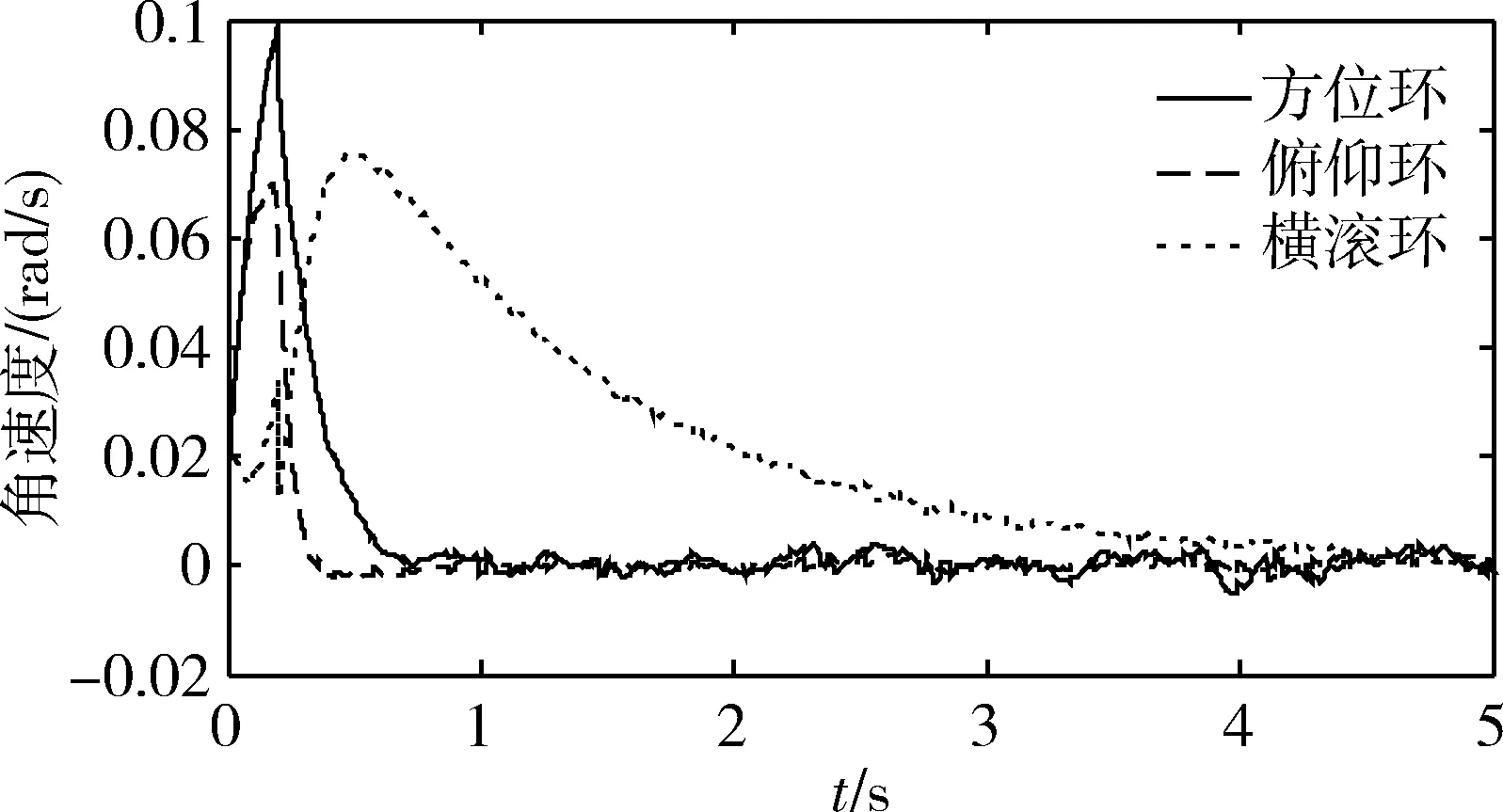
图6 τε=τε+10%τε时仿真结果

图7 τε=τε-10%τε时仿真结果

5 结论

对光电跟瞄平台的方位、俯仰及横滚环的稳定回路基于LMI算法，通过加权矩阵的选取，分别完成了输出反馈H∞稳定控制器的设计，仿真结果表明：外界扰动作用下，不存在模型参数摄动时，系统具有良好的稳态及动态性能，加上角振动扰动之后，稳态性能会差一点，但仍满足稳定控制要求,在控制指令作用下，系统输出能够实现快速跟踪且稳态误差较小；同样干扰作用下，模型参数存在摄动时，该系统的控制效果几乎不受影响。由此可见，输出反馈H∞控制可以满足三自由度光电跟瞄系统稳定控制的性能要求，且不存在状态信息不好测量的缺点，对外界扰动不敏感，具有良好的鲁棒性。

参 考 文 献

[1] 黄昌霞，李奇等.高精度稳定平台伺服控制系统设计与实现[J].航空兵器，2011,(1):23-27.(Huang Changxia, Li Qi, et al.Design and Realization of High-Precision Stabilized Platform Servo Control System[J].Aero Weaponry, 2011,(1):23-27.)

[2] 官柏林，贾建援，朱应敏.基于自适应遗传算法的三轴光电跟踪策略[J].仪器仪表学报，2012,33(8):1758-1763.(Guan Bolin, Jia Jianyuan, Zhu Yingmin. Tracking Strategy of Three-axis Photoelectric Tracking System Based on Adaptive Genetic Algorithm[J]. Chinese Journal of Scientific Instrument, 2012,33(8):1758-1763.)

[3] 聂光戍，魏瑞轩等.模糊自适应PID在机载激光武器光电跟瞄系统中的应用[J].弹箭与制导学报，2013,33(2):121-124.(Nie Guangshu, Wei Ruixuan, et al. Application of Fuzzy Self-adaptive PID Controller in the Tracking and Pointing System of the Airborne Laser Weapon[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013,33(2):121-124.

[4] Huang Jiaoru, Xie Guo, Yang Hengzhan.Robust Adapt Control for Dynamic Systems with Mixed Uncertainties[J].Journal of Systems Engineering and Electronics,2016,27(3):656-663.

[5] 刘珊中，李燕凡，刘永斌等.光电跟瞄平台稳定控制器设计[J].火力与指挥控制，2016,41(12):142-145.(Liu Shanzhong, Li Yanfan, Liu Yongbin et al. Stability Controller Design of Electro-optical Tracking and Pointing Platform[J]. Fire Control & Command Control.2016,41(12):142-145.)

[6] Rami A. Maher,Ismail A. Mohammed.Polynomial Based H∞Robust Governor for Load Frequency Control in Steam Turbine Power Systems[J]. International Journal of Electrical Power and Energy Systems,2014,57(5):311-317.

[7] 刘珊中，孙隆和，车宏.H∞控制在机载光电跟瞄系统中的应用[J].火力与指挥控制,2007.32(12):114-116,132.(Liu Shanzhong, Sun Longhe, Che Hong. Application of H∞Control to Airborne Electro-optical Tracking and Pointing System[J]. Fire Control and Command Control, 2007,32(12):114-116,132.)

[8] Guo Shuxiang. Robust Reliability Based Optimal Design of H∞Control of Parametric Uncertain Systems[J]. Journal of Dynamic Systems, Measurement, & Control, 2014,136(2):1-7.

[9] J.M.Michelin,P.Coustal,Control of A Sight System Flexible Structure A H∞Design[C], IEEE Proceedings of Decision and Control Conference, 1991,4.

[10] 宋世军，蜂聚呢，孟敏.受控正系统的弹性静态输出反馈鲁棒H∞控制[J].控制理论与应用，2014,31(5)：671-676.(Song Shijun,Feng June,Meng Min. Resilient Static Output Feedback Robust H∞Control for Controlled Positive Systems[J]. Control Theory & Applications, 2014,31(5):671-676.)

[11] 顾荃莹，宋建梅.导弹鲁棒H∞输出反馈姿态跟踪控制器设计[J].兵工学报，2007,28(6):682-685.(Gu Quanying, Song Jianmei. Design of a Missile Attitude Tracking Controller Based on H∞Robust Output Feedback[J]. ACTA Armamentarii, 2007,28(6):682-685.