基于时序模拟的孤岛微电网频率及电压质量评估

肖少华，朱庆龙，杨家豪

（1.国网浙江省电力有限公司嘉兴供电公司，浙江 嘉兴 314000；2.厦门中建东北设计院有限公司，福建 厦门 361000；3.厦门大学嘉庚学院，福建 厦门 361000）

0 引言

近年来，微电网技术得到了快速发展。微电网根据运行方式分为并网运和孤岛，当微电网工作在孤岛运行模式时则称为孤岛微电网，孤岛微电网为解决与主网距离较远的偏远地区的供电问题提供了有效途径[1-2]，有助于提高供电可靠性，我国也相继建设了一系列示范工程[3-4]。

由于光伏、风电等DG（分布式发电装置）的出力往往具有较强的间歇性，同时负荷也存在波动，会对孤岛微电网的频率及电压质量造成影响，进一步可能对系统运行的安全性造成威胁[5-6]。因此，对孤岛微电网的频率及电压质量进行合理评估显得意义重大。文献[7-8]介绍了孤岛微电网潮流模型的建立，其中文献[9]介绍了基于信赖域算法，提高潮流计算收敛性。文献[10]介绍了类奔德斯分解方法，较好地提升了潮流收敛速度。这些文献为孤岛微电网的潮流分析提供了基础。文献[11]介绍了基于时变通用生成函数对孤岛运行模式下微电网的可靠性进行评估；文献[12]介绍了基于时序模拟的离网型微网可靠性分析方法。计及时序特性能够更真实地反映典型情况下电源、负荷变化规律以及微电网的实际运行状态，使得频率及电压质量的评估结果更具有可信度。

以下提出一种基于时序模拟的频率及电压质量评估方法。根据实测的光伏、风电出力曲线、负荷曲线及采样点，逐点进行孤岛微电网潮流计算，从而对系统的实际运行状态进行时序模拟，获取系统频率、电压的变化曲线及概率分布情况，利用频率及电压偏差指标评估孤岛微电网的频率及电压质量。以Benchmark 0.4 kV低压微电网作为算例系统，验证该方法的有效性。

1 孤岛微电网潮流计算

1.1 潮流方程

孤岛微电网潮流计算是后续进行时序模拟的基础，此处孤岛微电网潮流模型中将具有恒电压控制功能的节点设为PV节点，其余节点均视为PQ节点。其中PQ节点需列写有功与无功平衡方程，PV节点仅需列写有功平衡方程，方程形式为：

式中：PCi和QCi分别为节点i恒功率电源注入的有功和无功，例如风光等采取最大功率点跟踪控制方式的DG属于此类电源；PDi和QDi分别为节点i采取下垂控制策略的设备注入的有功和无功，例如孤岛模式下的柴油发电机、燃气轮机、储能等均属于此类电源；PLi和QLi分别为节点i的有功与无功负荷；Pi和Qi分别为节点i注入的总有功功率和无功功率。

而节点注入的有功与无功功率为：

式中：n为节点数目；Gij与Bij分别为节点导纳矩阵的实部与虚部；δij为节点i和节点j的相角差。

1.2 采取下垂控制策略设备的注入功率

采取下垂控制策略的设备将通过测量系统当前频率及并网点电压，根据斜率调节输出有功及无功功率，其注入的功率可为：

式中：PDimax，QDimax分别为节点i具有下垂控制特性的设备注入的有功和无功最大值；fmax，fmin，Umax，Umin分别为系统频率、电压允许上下限；f0，f，U0，Ui分别为系统频率、电压的空载值与实际值。

1.3 计及频率电压静特性的负荷功率方程

对负荷进行建模时计及负荷的频率和电压静特性，负荷使用恒阻抗、恒电流和恒功率的组合模型来描述，可表示为：

式中：PLNi和QLNi分别为节点i在额定工况下的有功与无功负荷；UNi和fN分别为额定电压与频率，取 UNi=1 p.u.， fN=1 p.u.； Pi和 Qi分别为节点 i注入 的 总 有 功 功 率 和 无 功 功 率 ； Api， Bpi， Cpi， Aqi，Bqi，Cqi分别为负荷有功与无功功率中恒阻抗型、恒电流型、恒功率型的百分比系数，各满足总和为1；kLpi，kLqi分别为负荷的有功和无功功率的静态频率调节系数。

1.4 基于牛顿—拉夫逊法的潮流求解

采用牛顿—拉夫逊法求解潮流方程组，修正方程简写为：

式中：ΔP，ΔQ为节点有功与无功不平衡量；Δf，Δδ，ΔU为分别为频率、相角、电压的修正量；J为雅克比矩阵，其分块矩阵分别为：

2 基于时序模拟的评估方法

2.1 理论基础

采取序贯蒙特卡洛法进行孤岛微电网运行的时序模拟。蒙特卡洛仿真法尤其适合用于系统运行复杂和影响因素众多的情况。常规的非序贯蒙特卡洛仿真法通过随机抽样得到系统状态，不考虑时间上的连续[13-14]；而序贯蒙特卡罗法可以仿真系统运行状态转移和时序变化因素对系统运行的影响。

2.2 评估指标

由于微电网缺乏主网支撑，其电能质量往往难以保证，尤其是频率及电压质量。定义2个偏差指标用于评估孤岛微电网的频率及电压质量。

（1）频率偏差指标 Df。

式中：fk为第k个采样点潮流计算获得的稳态频率；N为采样点总数。

（2）电压偏差指标 DUi。

式中：Uik为第i个节点第k个采样点潮流计算获得的节点电压。

上述2个指标均反映了仿真时段内频率、电压与额定值相比的总体偏差情况，偏差指标越大，表明电能质量越差。

2.3 评估流程

评估方法流程图见图1，具体流程为：

（1）输入基础数据，例如微电网网架参数以及下垂控制电源的参数等。

（2）输入光伏、风力发电的出力序列，输入各节点的负荷序列。

（3）开始逐点代入式（1）—（10）对应的潮流方程中，进行潮流计算，并保存系统频率及各节点电压。

（4）根据式（11）—（12）计算频率偏差指标以及电压偏差指标，输出评估结果。

3 实例分析

以Benchmark 0.4 kV低压微电网作为算例系统，如图2所示。其中断路器S1打开，S2闭合，构成孤岛微电网系统。系统基准容量取100 kVA，假定孤岛微电网的安全运行范围为fmax=1.004 p.u.，fmin=0.996 p.u.， Umax=1.05 p.u.， Umin=0.95 p.u.。

接入设备参数见表1，其中节点L13—节点L17的电源中，光伏及风电采取MPPT（最大功率点追踪控制）的控制方式，在单个采样点潮流计算中视为恒功率电源，而其他的燃料电池、微型燃气轮机等采取对等控制，共同参与微电网频率及电压的调节。

负荷参数见表2，给出参数为负荷峰值。各节点恒阻抗、恒电流、恒功率负荷占比统一取为0.3，0.3，0.4，静态频率调节系数取 kLpi=2，kLqi=-2[8]。

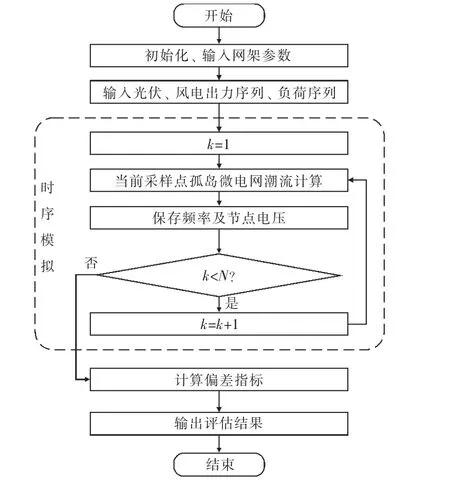
图1 评估流程

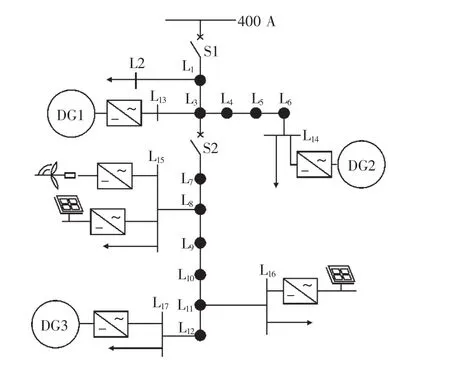
图2 Benchmark 0.4 kV低压微电网系统

表1 算例中接入的设备及参数

仿真所使用的光伏、风电出力序列以及负荷序列均来源于实测数据，时间长度为1周，时间间隔为15 min，总计672个采样点，见图3。由图3可知，光伏出力和负荷均呈现一定的规律性，但光伏与风电出力也具有一定间歇性，将造成孤岛微电网的功率波动。

表2 负荷参数

图3 DG出力及负荷曲线

通过逐点进行潮流计算，可以获得频率及电压的变化趋势，1周时间内系统的频率曲线如图4所示。

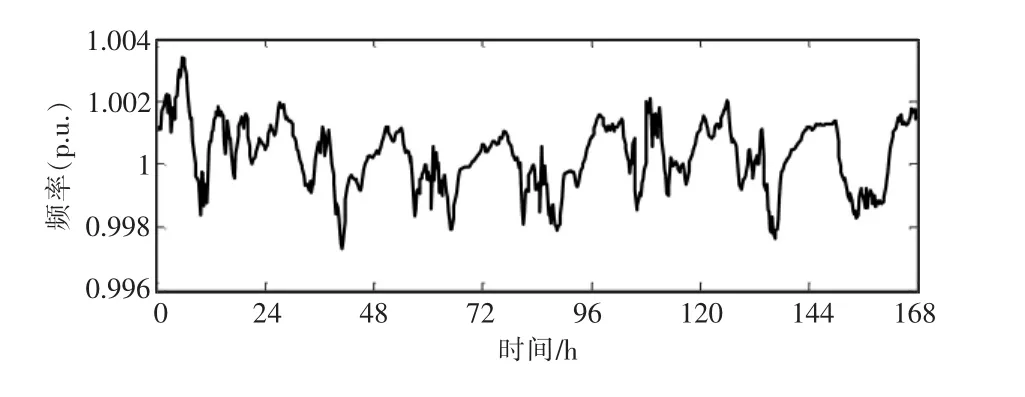
图4 频率变化曲线

由图4可知，由于该微电网源荷匹配合理，且各电源具有较为合理的调节裕度，能够较好地完成微电网调频的任务，系统频率均处于上下限范围内。但由于电源与负荷的波动性仍然可能在某些时段出现较大偏差，将全部采样点的计算结果进行统计，获得PDF（概率密度函数）和CDF（累积分布函数），如图5所示。可见，频率基本接近于在额定范围附近呈正态分布，偏差较大的概率较低，因此频率质量较好。

将上述仿真场景定为场景1，再增加2种场景以分析频率偏差指标对频率质量评估的有效性。其中场景2为在场景1基础上负荷加重10%，场景3为在场景1基础上让节点15的光伏故障退出运行。3种场景下的频率偏差指标见表3。

图5 频率的PDF及CDF

表3 各场景频率偏差指标

由表3可知，在场景2下负荷加重，系统运行频率降低，因此频率偏差增大，频率质量下降。而场景3由于30 kW光伏退出运行，会增加其他下垂控制电源调频的负担，因此频率偏差也增大，频率质量同样下降。由此可见，频率偏差指标对衡量频率质量是有效的且准确的。

场景1下的各节点电压偏差指标如表4所示。

表4 各节点电压偏差指标

由表4可知，不同节点的电压偏差总体情况存在差异，即电压质量不同。其中节点13电压偏差指标最小，而节点17最大。节点13与节点17的电压变化曲线见图6、图7。

由图6、图7可知，节点13与节点17变化趋势基本相同，但节点13整体电压高于节点17，原因是节点13是燃料电池接入点，且无负荷，是功率注入点，电压较高；而节点17负荷重且处于末端，电压偏低。节点13电压均在合格范围内，而节点17电压出现部分时间越下限的情况，电压质量较差，统计出PDF及CDF如图8所示。由此可知，以电压偏差指标评估微电网中各节点的电压质量是有效的。

图6 节点13电压变化曲线

图7 节点17电压变化曲线

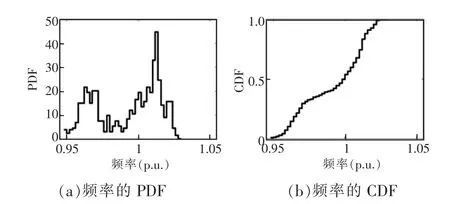
图8 节点17电压的PDF及CDF

4 结语

针对孤岛微电网的运行评估问题，提出了一种基于时序模拟的频率及电压质量评估方法。经过算例分析，得到如下的结论：

（1）该方法计及光伏、风电出力以及负荷的时序性，能更真实地反映系统实际运行状态对频率及电压质量的影响。

（2）所提出的频率及电压偏差指标能正确反映不同情况下系统的频率及电压质量，因此此处所提方法是合理有效的。

综上所述，该方法能够有效评估孤岛微电网的频率及电压质量，为孤岛微电网的规划设计及运行调整提供参考与指导。

参考文献：

[1]陈荣柱，林世溪，孙景钌，等.孤立海岛微电网供电模式下的柴油发电系统改造方案研究[J].浙江电力，2014，33（6）∶1-5.

[2]赵深，孙景钌，林世溪，等.海岛微电网供电模式下户用风光互补发电系统的应用研究[J].浙江电力，2014，33（5）∶22-26.

[3]王成山，周越.微电网示范工程综述[J].供用电，2015，31（1）∶16-21.

[4]郑漳华，艾芊.微电网的研究现状及在我国的应用前景[J].电网技术，2008，51（16）∶27-31.

[5]杨家豪.基于一致性算法的孤岛型微电网群实时协同功率分配[J].电力系统自动化，2017，41（5）∶8-15.

[6]彭寒梅，曹一家，黄小庆.对等控制孤岛微电网的静态安全风险评估[J].中国电机工程学报，2016，36（18）∶4837-4846.

[7]MUMTAZ F，SYED M H，HOSANI M A，et al.A novel approach to solve power flow for islanded microgrids using modified Newton Raphson with droop control of DG[J].IEEE Transactions on Sustainable Energy，2015，6（12）∶1-11.

[8]潘忠美，刘健，石梦，等.计及电压/频率静特性的孤岛微电网电压稳定性与薄弱节点分析[J].电网技术，2017，41（7）∶2214-2221.

[9]彭寒梅，曹一家，黄小庆.基于BFGS信赖域算法的孤岛微电网潮流计算[J].中国电机工程学报，2014，34（16）∶2629-2638.

[10]李培帅，施烨，吴在军，等.孤岛微电网潮流的类奔德斯分解算法[J].电力系统自动化，2017，41（14）∶119-125.

[11]彭寒梅，曹一家，黄小庆，等.基于时变通用生成函数的孤岛运行模式下微电网可靠性评估[J].电力系统自动化，2015，39（10）∶28-35.

[12]王杨，谢开贵，胡博，等.基于时序模拟的离网型微网可靠性分析[J].电工技术学报，2016，31（6）∶206-211.

[13]丁明，李生虎，黄凯.基于蒙特卡罗模拟的概率潮流计算[J].电网技术，2001，25（11）∶10-14.

[14]段玉兵，龚宇雷，谭兴国，等.基于蒙特卡罗模拟的微电网随机潮流计算方法[J].电工技术学报，2011，26（S1）∶274-278.