基于SOGI-PLL锁相技术的磁阀式可控电抗器运行特性研究

童 力，何立群，赵建文，吕春美，范学良，王笑棠

（1.国网浙江省电力有限公司电力科学研究院，杭州 310014；2.苏州大学轨道交通学院，江苏 苏州 215006；3.国网浙江省电力有限公司丽水供电公司，浙江 丽水 323000）

0 引言

随着我国超高压、远距离输电网的快速发展，以及多元化、大容量负荷的接入，无论是高压输电侧，或是中低压供配电侧，都需要大量快速响应的无功补偿装置进行电压/无功调节以维持电网的动态无功平衡[1-3]。在诸多基于电力电子技术的静止无功补偿装置中，MCR（磁阀式可控电抗器）的应用越来越受到关注。MCR通过控制直流回路的激磁改变铁心的饱和度，达到近乎平滑调节无功输出的目的。其容量调节容易实现，运行维护简单可靠，对抑制工频过电压、补偿线路容性无功、增强系统稳定性、提高输电能力等方面具有良好的改善作用，逐步在工程中获得了应用，如配电网无功补偿，电气化铁路无功补偿，电压闪变抑制等[4-9]。

MCR通过调节1对整流晶闸管导通和关断，并经自身绕组耦合建立直流励磁，调节铁心磁阀的饱和程度，进而改变其等效电抗，达到连续调节无功功率输出的目的。为了保证无功控制的精度，获取准确电网电压的相位信息尤为重要。由于电力系统中存在大量的非线性负载，电网电压不可避免包含谐波分量[10]。若仍采用传统的过零鉴相方式获得晶闸管触发的同步信号，将导致控制结果出现误差。因此，在电力电子装置数字化和智能化高速发展的背景下，采用高性能锁相方法准确获取电网电压基波相位具有可行性及实用意义。

MCR相关文献中对其锁相方法的介绍较少，考虑到牵引供电这类单相电网中电压波动、谐波污染等影响更为严重，而单相PLL（锁相环）的快速、准确控制比三相PLL更难实现[11]，因此以单相MCR的PLL方法为研究对象，采用基于级联型二阶广义积分的旋转坐标变换锁相方法，对PLL的整体方案、MCR工作电压包含谐波时的锁相性能进行了分析。

下面首先介绍磁阀式可控电抗器MCR的基本工作原理，明确电压相位是MCR控制过程中一个重要的信息，然后介绍级联二阶广义积分构造正交信号实现SRF-PLL（同步旋转坐标系锁相）方法对单相电压的锁相。最后，利用仿真实验研究了电网电压包含谐波情况下锁相的精度和MCR的工作特性。

1 MCR的控制特性

图1为单相MCR的结构示意图。电抗器由2个相同的主铁心1与2和旁轭组成。每个主铁心上绕有总匝数为NA的上、下2个绕组，每个绕组各有1个抽头分别与晶闸管VT1，VT2相连，抽头比δ=N2/NA，NA=N1+N2。不同铁心的上、下2个绕组交叉顺连后并联至电网，续流二极管VD跨接在2个绕组的交叉处。铁心1、铁心2分别与旁轭组成2条交流磁通的回路，铁心1和铁心2一起则组成直流磁通的回路。

MCR中1对晶闸管的触发控制方式如图2所示。以其端电压，即工作电压v的基波相位为同步信号，触发角为α，VT1与VT2分别在正、负半周触发开通。根据文献[1]可知，MCR中铁心的饱和度β随触发角α变化的关系为：

图1 单相磁阀式可控电抗器结构示意

图2 MCR触发控制

当工作电压为额定电压时，得到输出的无功功率标幺值：

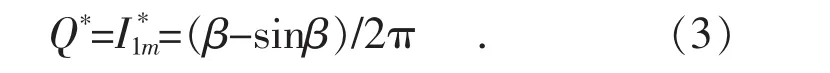
结合式（1）与（2）可知， 当 α=180°时 β=0， Q*=0， MCR 处于空载状态； 当 α=0°时 β=2π， Q*=1，MCR处于满载状态。通过调节触发角α即可调节直流偏磁大小，进而改变MCR两个铁心中磁阀的磁饱和程度，最终实现MCR输出感性电流（容量）的连续平滑调节。

2 级联SOGI-SRF型同步锁相技术

图3 单相系统中的旋转坐标系锁相法

基于SOGI（二阶广义积分）的正交信号产生器，其基本结构如图4所示，对输入信号v与输出信号v′相减，乘以系数k，利用SOGI实时构造出qv′，实现了输入信号与输出信号的正交化，同时对输入信号兼有滤波效果[14]。但是在实际中电网电压的波形畸变、以及信号采样引入的直流偏置，SOGI正交信号产生器的性能会受到影响，间接引入相位跟踪稳态误差，影响MCR的控制特性。为此，将2个SOGI模块进行级联。如图5所示，前一级SOGI输出信号v′作为后一级SO GI的输入，构成级联Cascade SOGI-QSG。后一级SOGI的输出 v″和 qv″用于 PLL。

图4 基于SOGI的正交信号发生器QSG

图5 级联型正交信号发生器SOGI-QSG

图5中所示级联SOGI，以复变量s为变量，其输出v″和qv″对输入的传递函数表达式分别为：

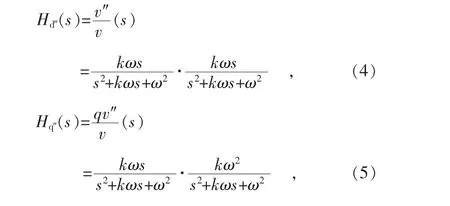
取前后两级SOGI中的系数k=1.414，其波特图如图6所示，Hd″（s）在谐振频率ω处对输入信号原样输出，无相位滞后，相比于Hd（s），低频段和高频段衰减增强。而Hq″（s）在谐振频率处仍然获得等幅的正交信号， 相位滞后 90°， 相比于 Hq″（s），高频段衰减增强，更为显著的是，Hq″（s）低频段由低通变为衰减，k越小，衰减越强。将以上思路进行扩展，增多级联SOGI的个数，构成多级SOGI，获得强滤波能力。

忽略前级SOGI的时间常数，考虑到后级SRF-PLL的小信号模型是一个标准的二阶系统，选取参数要动态响应、稳态特性之间做出折衷，工程中依据二阶最佳取阻尼比0.707。

3 非理想电网条件下基于SOGI-PLL的MCR工作特性

由于电力系统中存在大量非线性负载，使得电网电压中常常含有大量5次、7次等低次谐波。以一台单相MCR为例，采用提出的SOGI-PLL锁相方法，通过仿真验证其在电网电压包含低次谐波的非理想条件下的工作情况。以某台实际MCR设备参数为例，系统参数如表1所示。

在Matlab/Simulink仿真软件中，采用多绕组变压器模块，设置其磁化曲线饱和参数，可构造MCR的等效仿真模型[15]。MCR在额定触发角下的启动过程如图7所示，表明结合该锁相环MCR能够正常工作，稳态时工作电流幅值约233 A，与其额定参数吻合。

如图8中所示仿真结果，先使MCR在理想电网电压条件下工作在额定状态，随后给电网注入5次、7次谐波。可以看出电网电压发生畸变后，若仍采用过零锁相将导致误发触发脉冲。图8（a）表明采用提出的SOGI-SRF-PLL，电网电压畸变后能迅速锁定基波相位，使MCR控制系统正常工作。 图8（b）和图8（c）表明得益于锁相环的快速响应，MCR再次进入稳态的过渡时间不超过1个工频周期，同时无功功率输出保持在额定值。图8（d）给出了锁相角度的误差曲线。从图中可以看到锁相误差平均值保持为零，当电网电压注入谐波后误差中出现了少量谐波频率分量，总的来说误差限制在±2°以内。这是由于PLL算法所用的控制器为PI控制器，在进一步研究中可以考虑嵌入重复控制等算法进一步消除稳态误差。

图6 级联型SOGI的频率响应曲线

表1 仿真用的单相MCR系统参数

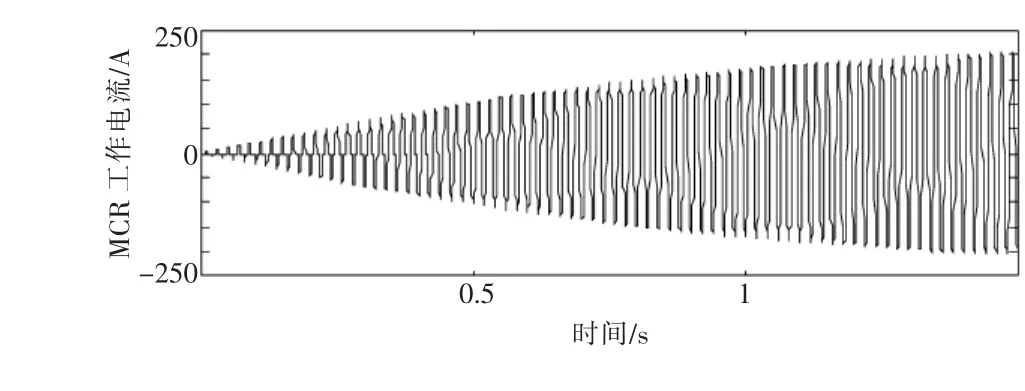
图7 MCR启动过程中的工作电流

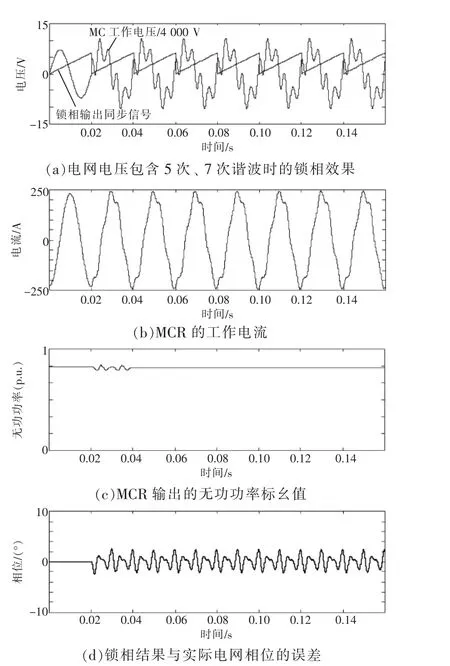
图8 仿真结果

图9展示了在不同的静态工作点下，锁相误差带来的触发角偏差造成的输出无功偏差。其中实线、虚线和圆点连线分别表示额定触发角α=60°，45°和20°时触发相位偏差与无功输出误差之间的关系。显然相位误差越大带来的无功偏差越大，两者之间呈现非线性关系。当触发角较大时，实际工作容量随相位误差增加而下降得更快。以触发角偏大10°带来的无功容量偏差为例，当额定触发角20°时实际无功输出会减少0.83%，额定触发角为45°时实际输出减少3.42%，而额定触发角为60°时实际无功输出则减少5.85%。

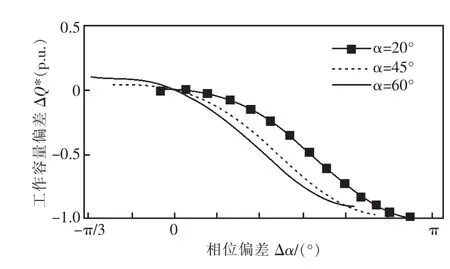
图9 触发相位偏差与工作容量偏差关系

4 结语

磁阀式可控电抗器MCR因其可靠性高、连续可调的特性在电力系统无功补偿中得到越来越多的应用。当MCR触发控制角存在误差时将导致无功输出的误差，因此需要高性能的锁相技术以保证非理想的电网电压下能获得精确的同步相位信息。通过前级级联二阶广义积分正交信号生成单元，使得三相同步旋转坐标系下锁相方法应用于单相系统，为MCR的触发控制提供准确的相位基准。仿真结果表明所提出的锁相技术能很好的抑制电网电压谐波的影响，过渡过程仅为2个工频周期，相对MCR的响应速度，所占时间基本可以忽略。该方案可应用于牵引电网等单相供电系统的无功补偿。

参考文献：

[1]陈柏超.新型饱和可控电抗器理论及应用[M].武汉：武汉水利水电大学出版社，1999.

[2]M TÜMAY，T DEMIRDELEN，S BAL，et al.A review of magnetically controlled shunt reactor for power quality improvement with renewable energy applications[J].Renew able and Sustainable Energy Reviews，2017（77）∶215-228.

[3]H K TYLL，F SCHETTLER.Historical overview on dynamic reactive power compensation solutions from the begin of AC power transmission towards present applications[C].2009.

[4]江少成，常宇.几种静止型动态无功补偿（SVC）装置的性能及应用场合分析[J].浙江电力，2009，28（5）∶32-36.

[5]田铭兴，励庆孚，王曙鸿.磁饱和式可控电抗器的等效物理模型及其数学模型[J].电工技术学报，2002，17（4）∶18-21.

[6]TIAN MOMGXOMG.A Novel Quickness Improvement Method of a Magnetic-Valve Controllable Reactor[J].IEEE Trans actions on Applied Superconductivity，2017，26 （7）∶61-85.

[7]姚尧，陈柏超，田翠华.磁控电抗器在右江500 kV线路中的应用[J].高电压技术，2008，34（5）∶984-988.

[8]余韦彤，程汉湘，姜翠玲，等.磁阀式可控电抗器的电磁特性[J].广东电力，2014，27（5）∶95-98.

[9]陈宏伟，金涌涛，周啸波，等.基于110 kV电压等级的MSVC 无功电压控制[J].浙江电力，2014，33（4）∶14-18.

[10]T BEN，Q YANG，R YAN，et al.Magnetically Controlled Saturable Reactor Core Vibration Under Practical Work ing Conditions[J].IEEE Transactions on Magnetics，2017，53（4）∶820-904.

[11]D JOVCIC.Phase locked loop system for FACTS[J].IEEE Transactions on Power Systems.2003，18（3）∶1116-1124.

[12]CHUNG S K.A phase tracking system for three phase utility interface inverters[J].IEEE Transactions on Power Electronics，2000，15（3）∶431-438.

[13]MIHAI CIOBOTARU，REMUS TEODORESCU，FREDE BLAABJERG，et al.A New Single-Phase PLL Structure Based on Second Order Generalized Integrator[C]//IEEE Power Electronics Specialists Conference，2006.

[14]谢门喜，史炳伟.二阶广义积分单相电网电压锁相方法实验研究[J].电气自动化，2016，38（6）∶54-57.

[15]田铭兴，杨秀川，杨雪凇.基于MATLAB多绕组变压器模型的磁饱和式可控电抗器仿真建模方法[J].电力自动化设备，2014，34（3）∶78-81.