基于频率-波数滤波的联合多尺度全波形反演方法及其实现策略

黄建平, 崔 超, 刘梦丽

(1.中国石油大学地球科学与技术学院,山东青岛 266580;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛 266071)

由于固有的非线性特征,全波形反演对初始模型和地震数据中的低频成分具有较强的依赖性[1-2]。基于频率由低到高的多尺度反演(multi-scale full waveform inversion, MFWI)是提高全波形反演稳定性的有效方法[3-5],然而该方法仍然受限于地震数据中最低有效频率的大小[6]。受采集能力和处理技术的限制,实际地震数据中的低频成分往往不可靠。为此国内外学者提出利用包络[7-11]、小波变换[12]等方法恢复地震数据中的低频信息。Alkhalifah[13]指出,波形反演问题的关键在于保证反演波数的连续性。全波形反演能够恢复的波数成分不仅与地震数据的频率有关,还与地震波传播的散射角相关[6,14-16]。基于此,笔者在传统的时间域多尺度反演方法基础上,发展一种基于频率-波数滤波的联合多尺度反演方法(hybrid multi-scale full waveform inversion, HMFWI),利用大散射角信息弥补地震数据中缺失的低频成分,以降低传统全波形反演方法对低频数据的依赖性。

1 原 理

1.1 时间域全波形反演基本原理

基于L2范数的全波形反演方法的目标泛函[1,17]为

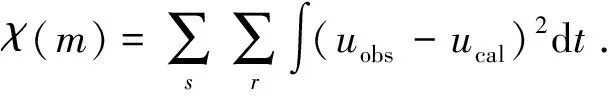
(1)

式中,uobs和ucal分别为由震源s激发在r接收点位置处t时刻的观测数据和正演数据;m为模型参数。

目标泛函关于模型参数的梯度项可以通过伴随状态法[18-19]求得:

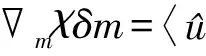
(2)

Sadj=ucal-uobs.

(3)

全波形反演通过对模型参数的迭代更新求得最优解,其迭代公式可以表示为

mk+1=mk-αkHkmχ.

(4)

式中,k为迭代次数;Hk为对梯度的修正项,可采用共轭梯度法、L-BFGS方法等,本文中采用共轭梯度法;αk为步长,可由抛物插值法获得[20]。

1.2 基于Wiener滤波器的多尺度反演方法

利用原始信号与目标信号的频谱信息,Wiener滤波器能够将源信号转化为十分接近目标信号的形式。Boonyasiriwate等[5]提出了基于Wiener滤波器的高效时间域波形反演方法,其中Wiener滤波器可以表示为

(5)

式中,Wtarget(f)为目标子波的频谱;Worigional(f)为原始子波的频谱;f为频率;ε为保证稳定性的极小值。在地震数据子波已知的情况下,利用Wiener滤波器可以将原高频地震数据转化为主频较低的数据,转化后的地震数据可以表示为

u′=F-1(WWiener(f)U(f)) .

(6)

式中,U(f)为原始地震记录的频谱;F-1为傅里叶反变换。

利用滤波器(5),并结合高效的反演频率选择策略[21],Boonyasiriwate等[5]实现了在时间域的多尺度全波形反演方法,其计算效率明显高于传统方法。然而通过对公式(5)分析可得,与一般的基于频率滤波的多尺度反演方法相同,Wiener滤波器不能对地震数据中缺失的低频信息进行恢复,因此其适用性在很大程度上依赖于地震数据的最低有效频率。在地震数据质量较差、低频信息缺失严重时,Wiener并不能缓解全波形反演的非线性问题。

1.3 基于Poynting矢量的多尺度反演方法

由地震波的散射理论可知[6,14],全波形反演对地下介质的分辨率主要与散射角θ(本文中参照Zhou 等[22]定义散射角)和地震波波长λ相关。因此对于低波数成分(背景场)的反演不仅仅依赖于地震数据的频率成分,也依赖于地震波的散射角信息。前人在此基础上提出了多种全波形反演的优化算法:由于大偏移距一般对应于大散射角信息,Shipp和Singh[23]提出利用数据加窗的方法,首先在早期反演大偏移距数据获得模型低波数组分,然后进行近偏移距数据反演的多尺度反演方法,然而该方法难以避免大偏移距数据的周波跳跃问题[24];Xie[6]以及Alkhalifah[15]等提出通过散射角信息对梯度滤波以控制模型更新的波数成分,但是在地震数据低频信息缺失或者数据采集质量不高时该方法的适用性有限[6];Alkhalifah和Wu[16]利用散射角滤波实现了梯度中背景速度成分与散射成分的分离,结合多次散射,以获得更加丰富有效的低波数成分。

如图1所示(其中KS、KR分别表示与震源、检波点相关的波数成分[28]),全波形反演模型波数与散射角和波长的关系可以表示为

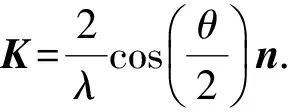
(7)

式中,λ为固有波长,由速度和频率决定;θ为散射角,主要取决于观测系统的分布;n表示波数K的方向。波长的定义为

(8)

式中,v为模型速度。由式(7)和(8)可得:一方面,在观测系统一定的条件下,反演所得到模型的波数成分主要取决于地震数据的频率成分,频率越低,反演所得到的波数成分越低;另一方面,在地震数据低频信息不足时,波形反演的低波数成分可以通过大散射角信息获得,如回折波,大偏移距的反射波等。

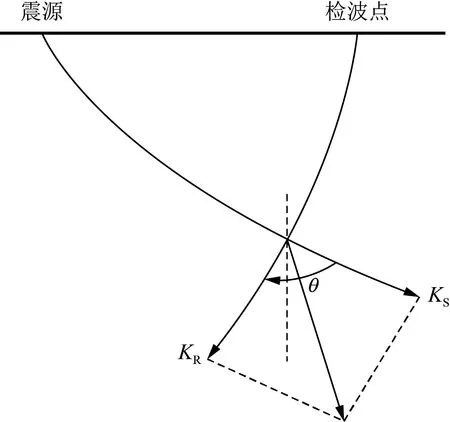
图1 全波形反演的波数成分与观测系统分布之间关系Fig.1 Relationship between wavenumber recovered by FWI and acquisition geometry

基于此,本文中通过设计与散射角相关的滤波器[6,15-16],对梯度项按照散射角信息进行滤波。在反演早期提取波场传播中的大散射角信息,首先获得较为准确的低波数模型,然后逐渐减小散射角,以增加模型中的高波数组分,并与传统的时间域多尺度反演相结合,来有效提高全波形反演在低频成分缺失情况下的稳定性和适应性。

本文中利用Poynting矢量实现对梯度根据散射角信息的滤波。Poynting矢量通过波场数据以及波场的时间、空间导数获得地震波的传播方向,在地震数据处理中被应用于去除逆时偏移中的低频噪音[25-26]、进行地震勘探的照明分析[27]、抽取共成像点道集[28-30]以及对全波形反演梯度的预处理[6]等方面。

在二维情况下,Poynting矢量[25]可以表示为

P(u)≅-

(9)

利用Poynting矢量可以获得震源波场与伴随波场之间的夹角余弦值:

(10)

利用震源波场与伴随波场的余弦值设计滤波器W(θ),将原有的梯度项表示为

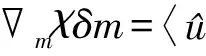
(11)

W(θ)形式可以表示为

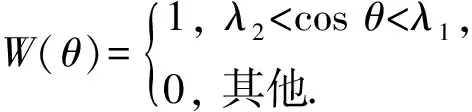
(12)

式中，λ1、λ2表示所期望的散射角余弦值范围,其取值范围为-1<λ2<λ1<1。

利用公式(11)能够有效控制梯度中的波数成分:在反演早期采用较小的λ1、λ2值,只保留大散射角信息,以保证背景速度场的有效更新,然后逐渐放宽λ1、λ2的范围,逐步对反演结果进行细化,实现基于波数滤波的多尺度反演方法。必须说明的是,滤波器W(θ)中参数λ1、λ2的确定是决定基于波数滤波的多尺度反演方法成败的关键因素。对于波数滤波中阈值的确定在诸多论文中有所涉及:Alkhalifah和Wu[16]利用波数信息控制背景场和扰动场的更新量;Xie[6]通过波数域的滤波实现了大尺度速度场的更新;Tang[31]等利用散射角信息实现了对全波形反演梯度中层析成分与偏移成分的加权重组以提高波形反演对中低波数组分的反演能力。然而前人并没有给出有效的滤波阈值的控制方法,仅仅说明波数阈值应该逐渐变化或者通过人为控制确定。由于波形反演中的关键问题是控制波数的连续性[13],而利用散射角对梯度中的波数成分进行控制时不存在类似于基于频率滤波的多尺度反演的高效算法[5,21]。因此本文认为,为了能够保证反演的准确性,应该在计算量允许的情况下尽可能地增加反演阶段。除此之外,还可以根据不同阶段目标泛函的收敛情况进行滤波阈值的确定,若前一阶段目标泛函收敛较慢,则可以适当增大滤波范围的变化量,反之则应当适当减小变化量。

1.4基于频率-波数滤波的联合多尺度全波形反演流程

综上所述,波形反演的低波数成分来源包括低频数据和大散射角信息。常规的基于频率滤波的多尺度反演方法对地震数据中的低频信息具有较强的依赖性,在低频数据缺失情况下往往反演失败;而仅仅利用波数滤波在地震数据主频较高时存在严重的周波跳跃问题。因此本文中提出两种基于频率-波数滤波的联合多尺度反演策略:一方面,通过首先对地震数据做低通滤波,可以有效避免单一波数滤波方法存在的周波跳跃问题,提高反演稳定性;另一方面,通过大散射角信息弥补地震低频数据缺失所不能恢复的低波数成分,能有效降低传统全波形反演方法对低频数据的依赖性,增强多尺度反演方法的适应性。

假设地震子波已知的情况下,策略一:将波数滤波与频率滤波分离,首先进行基于波数滤波的多尺度反演,在其提供较为准确的初始模型时,开始进行基于频率滤波的多尺度反演。其具体流程为:首先通过式(5)所示的Wiener滤波器对原始地震数据进行滤波,以获得其中相对低频的信息。然后利用公式(11)获得不同散射角下对应的梯度信息,散射角由大到小逐次迭代直到获得该频率下对应的所有波数成分(-1≤cosθ≤1)。最后利用传统的时间域多尺度反演方法对模型进行更新,在后续的频率成分反演中不对梯度项进行波数滤波,简记为HMFWI1。

策略二:将波数滤波与频率滤波交替进行,将整个反演分为内、外两个循环。将波数滤波作为外循环,内循环做频率由低到高的多尺度反演,然后逐渐增大外循环反演所用的散射角信息,直到获得所有的频率和散射角信息。相同的可以将频率滤波作为外循环,将波数滤波作为内循环,简称为HMFWI2。

具体的反演流程如图2所示,其中条件1表示目标泛函收敛或者反演次数达到上限,条件2表示频率滤波迭代完成,条件3表示波数滤波迭代完成。

本文中所采用的方法与Alkhalifah和Wu[16]所给波数滤波方法在思想上是类似的,即通过直接利用散射角信息对梯度中的波数成分进行控制,以达到控制模型更新的波数成分的目的。然而,除了所采用的滤波方法不同之外(本文中采用Poynting矢量方法,Alkhalifah和Wu[16]采用扩展成像方法),一方面,两者在低波数成分的来源上是不同的:Alkhalifah和Wu[16]利用波数滤波的目的在于对梯度场的分解,波数滤波起到阈值作用,以获得有效的背景场与散射场,其反演所获得的低波数成分来自于模型扰动场所得到的一次散射和多次散射成分。相比而言,本文中研究的重点在于给出一种频率-波数联合滤波的多尺度反演方法,在解决单一波数滤波周波跳跃问题的基础上弥补由于低频缺失不能恢复的低波数成分,通过两种滤波方法的联合作用直接获得低波数组分。另一方面,由于Alkhalifah和Wu[16]的方法需要构造较为有效的扰动场获得低波数梯度,如果在时间域进行会极大地增加计算量,相比而言本文中方法在计算量上具有一定的优势。

2 模型试算

为了验证本文方法的适用性,采用如图3所示的国际标准SEG/EAGE推覆体模型进行测试。首先验证传统多尺度全波形反演对低频信息的依赖性,然后将本文方法在低频数据缺失情况下进行测试。

具体的反演参数为:模型纵横向尺寸为1 km×4 km, 每200 m做一次正演模拟,共20炮,在海水表面从0开始每10 m放置一个检波器,共400个接收点。使用时间2阶,空间8阶有限差分正演模拟及PML边界条件做正演模拟[32-34]。地震子波采用主频为15 Hz的雷克子波,反演过程中给定震源子波和水层速度。对水层以下进行三角平滑并乘以0.9获得反演的初始模型(图4),初始模型与真实模型存在较大差异。

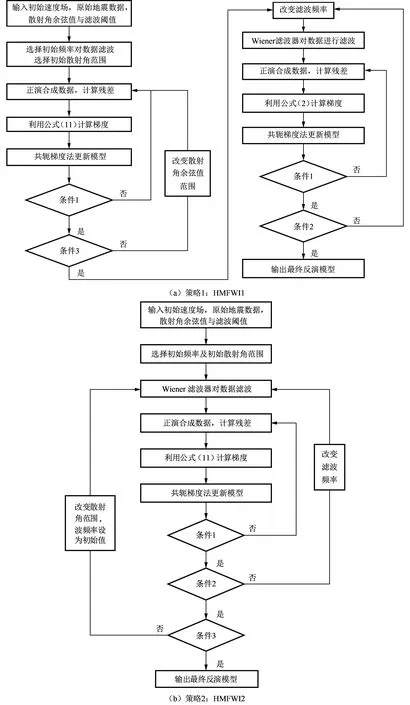
图2 两种联合多尺度全波形反演策略流程Fig.2 Workflows of two inversion strategies of hybrid multi-scale inversion

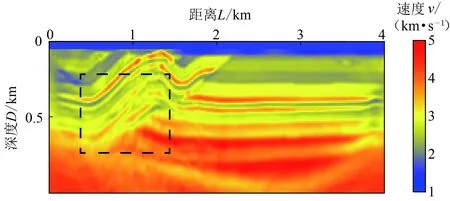
图3 真实模型:SEG/EAGE推覆体模型Fig.3 True model:SEG/EAGE overthrust model

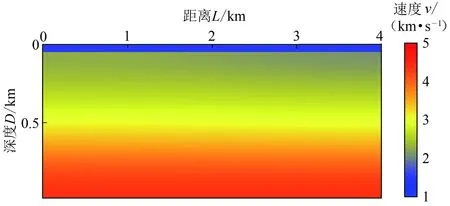
图4 反演所采用的初始模型Fig.4 Initial model for inversion

2.1 时间域多尺度反演方法对低频信息的依赖性测试

为了验证传统时间域多尺度反演方法对低频信息的依赖性,首先利用完整的雷克子波进行反演测试。完整的雷克子波的时间域波形与频率域频谱如图5中蓝色曲线所示,为了保证反演精度,所用的反演频率分别为5、8、11、14 Hz和全频段(利用Boonyasiriwate等[5]给出的频率选择标准,反演频率应该为5、15 Hz)。每个频率迭代10次,采用全频段时迭代直至误差泛函收敛。

对原始数据做时间域多尺度的全波形反演所得的最终反演结果如图6所示。可见由于观测系统偏移距较大,回折波作用较深,在回折波的作用区域反演结果与真实模型较为接近。尤其是在0.5 km以上,速度层位刻画较为精细,两个高陡断层反演较为准确。然而在中深层,由于初始模型与真实模型相差较远,并且回折波作用较弱,速度层间差异较小,反演效果较为模糊。在深度0.8 km以下范围内,尤其是在模型两侧,由于不能接收到来自于该区域的反射波信息,全波形对该区域速度更新及其微弱。总体而言,时间域多尺度反演方法较为成功地解释了地下的构造情况。

为了验证低频信息缺失对传统时间域多尺度反演的影响,采用高通滤波后的雷克子波作为震源子波,其频谱如图5(b)中红色实线所示,滤去6 Hz以下的低频信息,并在6～12 Hz之间加过渡带以保证稳定性,由其频谱可见低频信息损失严重。低频信息的缺失会导致时间域波形的高频抖动(图5(a)中红色实线),由于全波形局部极小问题主要来源于波形的复杂性,因此意味着局部极小的增多,非线性增强,反演难度增大。

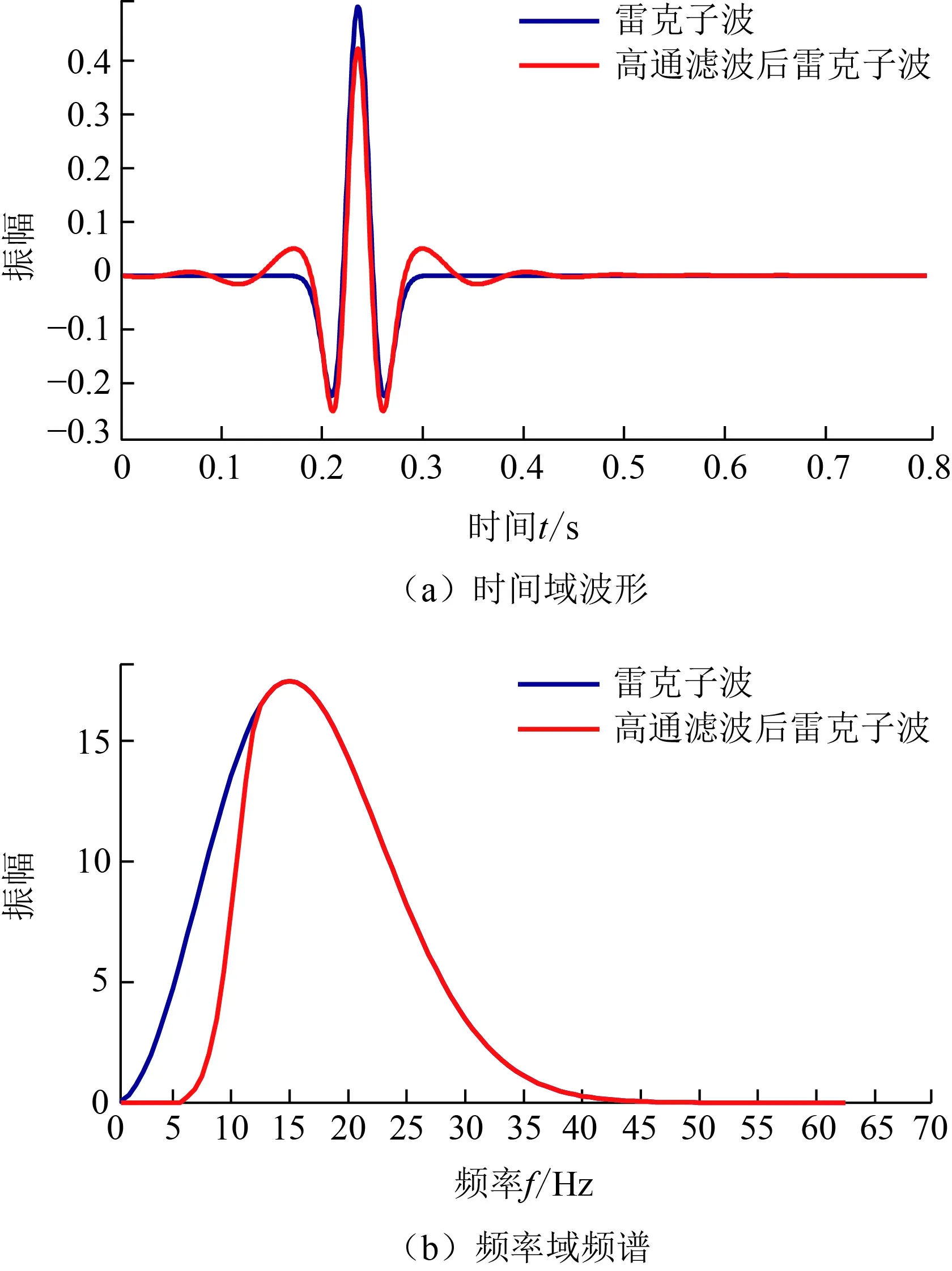
图5 高通滤波前后雷克子波对比Fig.5 Comparison of Ricker wavelets before and after using high pass filter

图6 全频带地震数据的时间域多尺度反演结果Fig.6 Inversion result of multi-scale full waveform inversion in time domain using full frequency banddata

采用与完整数据时完全相同的反演参数,低频数据缺失的时间域全波形反演结果如图7所示。对比分析可知,由于缺少低频信息所提供的低波数成分,传统的时间域多尺度反演方法仅在横向大于2 km的范围内对模型进行了有效更新,原因在于该区域构造较为简单并且回折波的穿透范围较深。在横向小于2 km范围内,由于模型构造较为复杂,反演结果在0.2 km以下的深层范围内几乎不能提供任何有效的构造信息,证明了在低频缺失情况下,传统的时间域多尺度全波形反演非线性问题严重,不能对模型进行有效更新,反演失效。

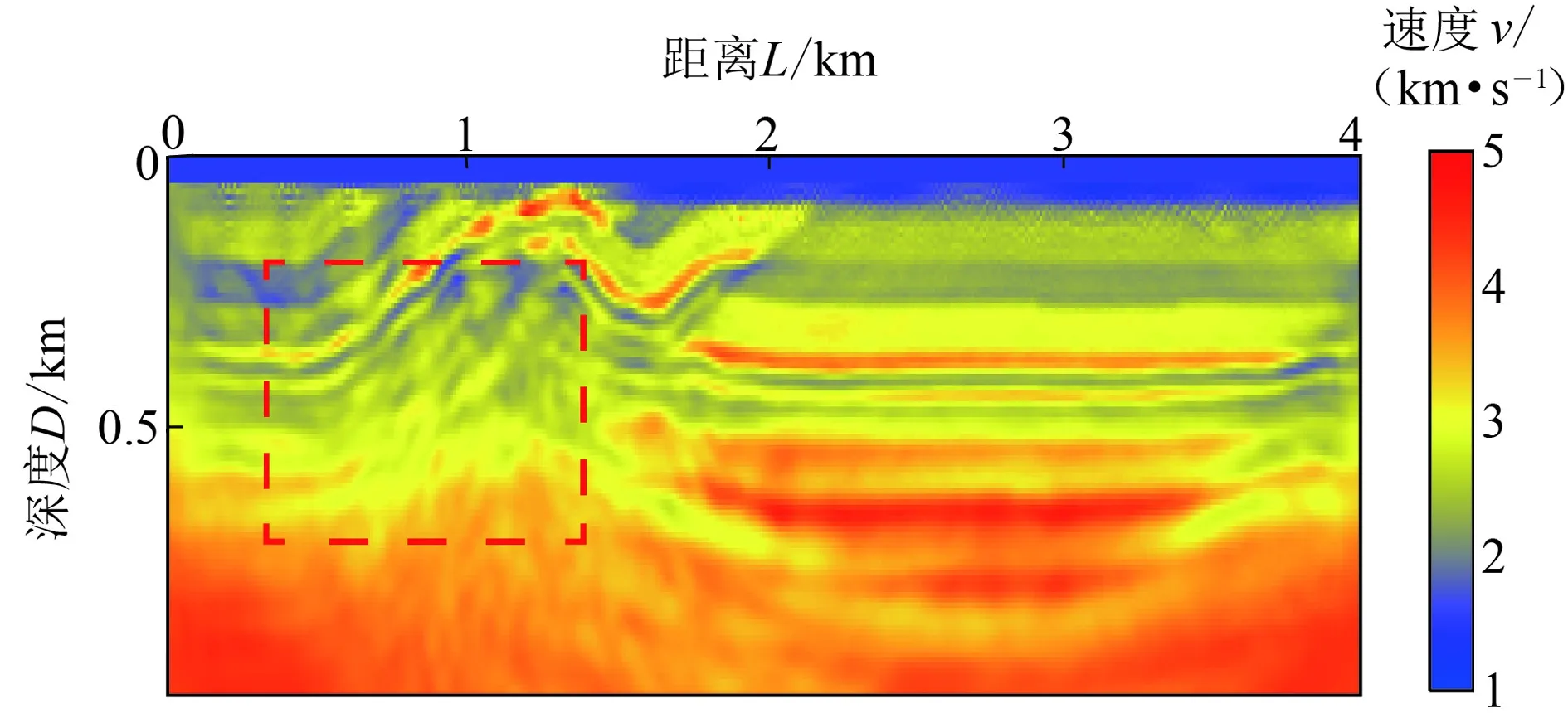
图7 低频数据缺失的时间域多尺度反演结果Fig.7 Inversion result of multi-scale full waveform inversion in time domain without low frequency data

2.2 基于频率-波数滤波的联合多尺度反演方法测试

在验证传统时间域多尺度反演方法对数据中低频信息具有较强依赖性的基础上,为了说明本文中方法的有效性,分别采用本文中提出的两种策略进行低频数据缺失情况下的反演测试。所采用的反演参数如下:①对于HMFWI1,为了保证反演结果的准确性,采用较为密集的滤波阈值采样。在散射角多尺度反演过程中将λ2固定为-1,λ1分别取-0.8,-0.5,-0.2,0.1,0.4,0.7,1。由于多尺度反演的每个阶段不一定要求目标泛函收敛,而仅需为下一阶段提供较为准确的初始速度场[16],且在反演早期更新背景场情况下目标泛函收敛较快,因此为了保证较高的计算效率,令每个阶段迭代5次。其次采用传统的时间域多尺度反演方法,为了保证反演精度,本文中采用等间隔的频率采样方法,所用的反演频率分别为5、8、11、14 Hz和全频段(符合Boonyasiriwate等[5]给出的频率选择标准),同样为了保证计算效率,每个频率迭代10次,采用全频段时迭代直至误差泛函收敛。②对于HMFWI2,将基于波数滤波的多尺度反演作为外循环,所采用的λ2、λ1值与HMFWI1相同,将传统时间域多尺度反演作为内循环,所采用的反演频率与HMFWI1相同。为了保证计算效率,每个频率段迭代5次,采用全频段和全散射角时迭代直至目标泛函收敛。

图8为HMFWI1和HMFWI2的反演结果。由图8可见:在低频数据缺失的情况下,相比于传统的时间域多尺度反演方法(图7),基于频率-波数滤波的联合多尺度全波形反演结果有明显提升,即使在低频信息缺失情况下也能得到较为准确的反演结果。无论是横向大于2 km的水平层位置还是较为复杂的褶皱区域,速度层位的刻画都较为精确。横向小于2 km处的高陡断层位置准确。

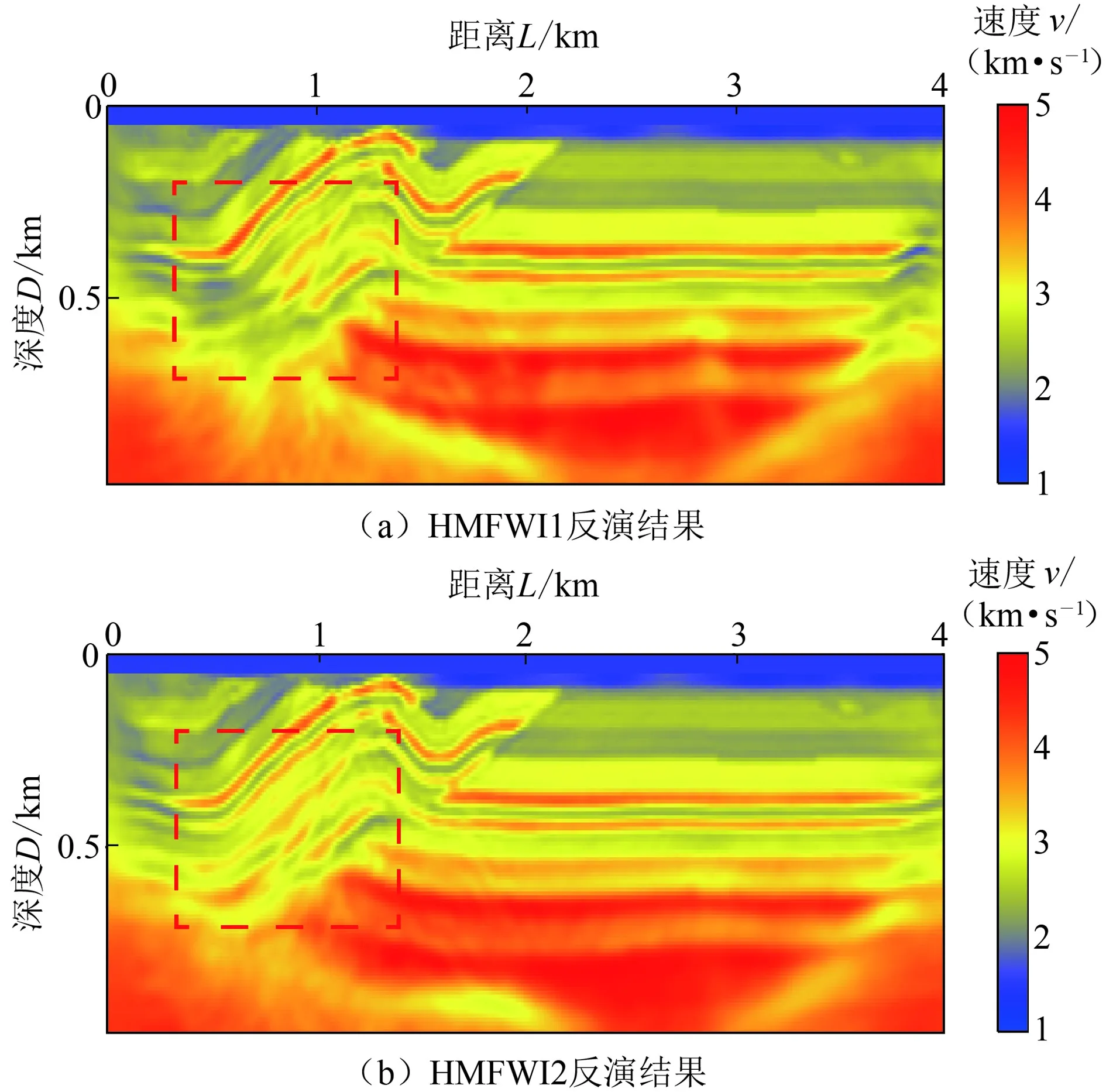
图8 HMFWI1和HMFWI2的反演结果Fig.8 Inversion results of HMFWI1 and HMFWI2

对比HMFWI1和HMFWI2两种方法反演结果可以发现,HMFWI2的反演结果(图8(b))要明显优于HMFWI1(图8(a)),尤其是在推覆体下部位置(图9)。究其原因可能是在以基于波数滤波的多尺度反演作为外循环时每个散射角循环可以利用所有地震数据的频率组分,因此能够恢复的波数成分也较为丰富,而HMFWI1在进行散射角多尺度反演时只能用到有限的频率成分(本例中为高通滤波后5 Hz雷克子波),因此能够恢复的波数成分有限。图10给出了所有散射角信息反演完成时HMFWI1和HMFWI2所得到的最终反演结果。相比而言HMFWI2的反演结果更为精确,模型中的主要构造的形态及反演绝对数值都更加接近真实速度场。

为了更加清晰的对比几种反演方法的差异,图11给出了位于1 km位置处的纵向速度剖面。通过观察可知:由于初始速度场与真实速度场相差较远,传统的时间域全波形反演方法仅能更新浅层(深度小于100 m)部分构造,而本文中提出的两种HMFWI方法能够进一步更新中、深部模型,极大提高了传统全波形反演的适应范围。同时,经过分析还发现,在模型深层反演效果方面,HMFWI2反演结果要略优于HMFWI1。

最后,为了证明本文中给出的反演策略相对于Xie[6]提出的基于角度域波数滤波器的多尺度全波形反演方法的优势,图12给出了通过对梯度进行波数滤波的多尺度全波形反演在低频数据缺失情况下的反演结果。可见反演结果没有体现任何有效的速度场信息,说明了在低频信息缺失的情况下,仅仅采用波数滤波不能避免周波跳跃问题。

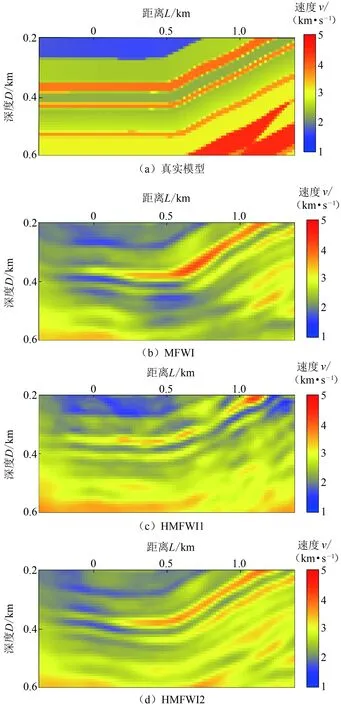
图9 速度场局部放大图Fig.9 Partial enlarged details of velocity field

需要说明的是,由于本方法要求在反演早期有较为可靠的大散射角信息,因此主要适用于大偏移距、速度场梯度较大的模型。在近偏移距情况下,可以利用偏移得到的偏移剖面作为先验信息获得大散射角信息[16,24]。在计算效率上,本文中方法要明显低于传统的时间域全波形反演,因此需要进一步探讨高效的反演策略以提高其对复杂介质[35]适用性。

图10 所有散射角反演后得到的速度模型Fig.10 Velocity models obtained after inversions using all scattering angles

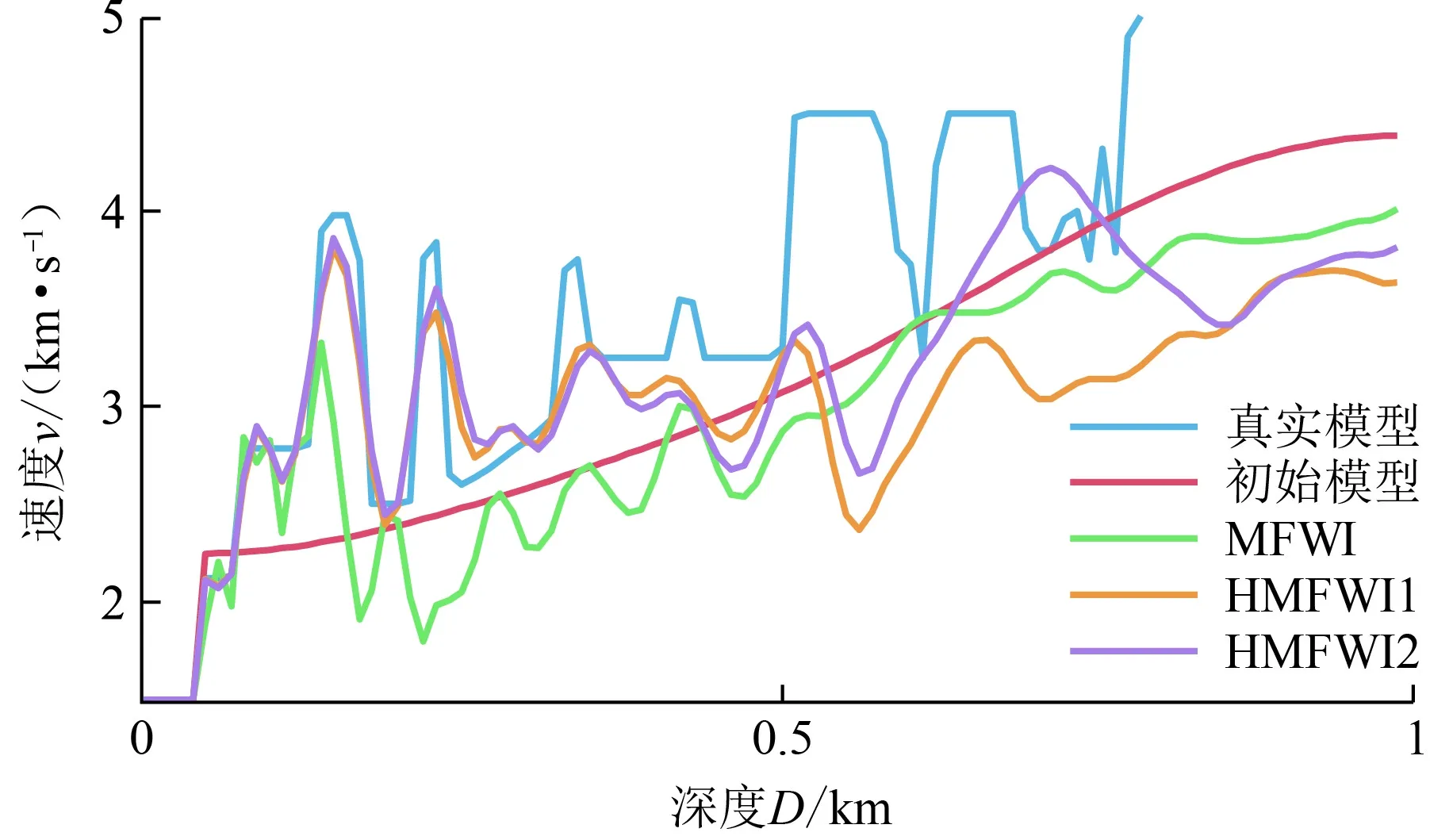
图11 横向1 km处抽得的纵向速度剖面对比Fig.11 Comparison of vertical velocity profiles at 1 km

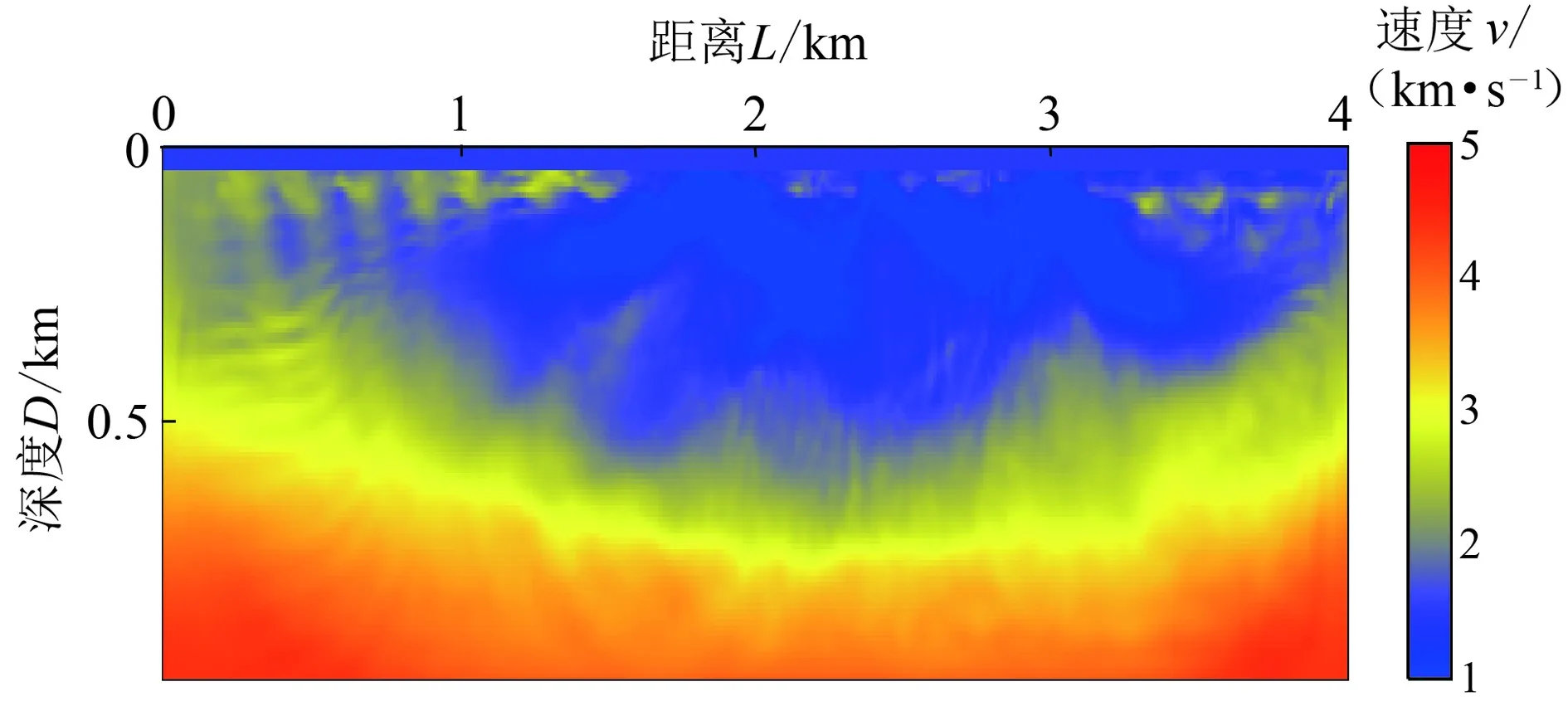
图12 由Xie[6]提出的“基于角度域波数滤波的多尺度全波形反演”结果Fig.12 Inverted result using “angle-domain wavenumber filter based full-waveform inversion (AWFWI)” proposed by Xie[6]

3 结 论

(1)波形反演的关键在于保证反演波数的连续性,当初始模型较差时,需要从地震数据中获得足够低的波数成分,以保证后续反演过程中观测数据与模拟数据误差不大于半个周期。

(2)传统的时间域多尺度反演方法通过由低频到高频递进反演,在反演早期获得较为准确的低波数组分,以提高波形反演问题的收敛性。但是该方法在本质上依赖于地震数据中的低频信息,在低频信息缺失或质量较差以及初始模型不能保证最低有效频率下的观测数据与模拟数据误差小于半个周期时,该方法反演失败。

(3)根据地震波散射理论,全波形反演能够反演的模型低波数成分不仅仅来源于低频数据,也可以来源于大散射角信息。因此当地震数据中低频数据缺失时,通过设计与散射角相关的滤波器,提取梯度中的大散射角成分,以弥补由于低频缺失不能恢复的低波数成分,能够保证后续反演收敛性。

(4)将基于波数滤波的多尺度全波形反演方法与传统的时间域多尺度全波形反演方法相结合,一方面可以有效弥补低频信息缺失时传统多尺度反演方法不能恢复的低波数成分;另一方面可以保证波数滤波反演方法能够避免周波跳跃现象。与传统的时间域多尺度全波形反演方法相比,本文方法即使在低频数据缺失情况下也能得到较为准确的反演结果,有效地降低了波形反演对低频信息的依赖性。

参考文献:

[1] VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J].Geophysics, 2009,74(6):WCC1-WCC26.

[2] FICHTNER A. Full seismic waveform modelling and inversion [M]. Heidelberg:Spinger-Verlag,2010.

[3] FICHTNER A. Multiscale full waveform inversion[J]. Geophysical Journal International, 2013,194(1):534-556.

[4] BUNKS C, SALECK F M, ZALESKI S, et al. Multiscale seismic waveform inversion[J]. Geophysics, 1995,60(5):1457-1473.

[5] BOONYASIRIWATC, VALASEK P, ROUTHP,et al. An efficient multiscale for time-domain wave form tomography[J].Geophysics, 2009,74(6):WCC59-WCC68.

[6] XIE X B. An angle-domain wavenumber filter for multi-scale full-waveform inversion: SEG International Exhibition and Annual Meeting, New Orleans, October 18-23, 2015 [C].Tulsa: Society of Exploration Geophysicists,2015.

[7] WU RS, LUO J, WU B. Seismic envelope inversion and modulation signal model [J].Geophysics, 2014,79(3):WA13-WA24.

[8] CHI B, DONG L, LIU Y. Full waveform inversion method using envelope objective function without low frequency data[J].J Appl Geophys, 2014,109:36-46.

[9] LUO J, WU R S. Seismic envelope inversion: reduction of local minima and noise resistance [J]. Geophysical Prospecting, 2015,63:597-614.

[10] 敖瑞德,董良国,迟本鑫.不依赖子波、基于包络的FWI初始模型建立方法研究[J].地球物理学报,2015,50(6):1998-2010.

AO Ruide, DONG Liangguo, CHI Benxin. Source-independent envelope-based FWI to build an initial model[J]. Chinese Journal of Geophysics, 2015,50(6):1998-2010.

[11] HUANG C, DONG L G, CHI B X. Elastic envelope inversion using multicomponent seismic data with filtered-out low frequency [J]. Applied Geophysics, 2015,12(3):362-377.

[12] YANHUA O Y, FREDERIK J S. Multiscale adjoint waveform-difference tomography using wavelets [J]. Geophysics, 2014,79(3):WA79-WA95.

[13] ALKHALIFAH T. Full-model wavenumber inversion: an emphasis on the appropriate wavenumber continuation[J].Geophysics, 2016,81(3):R89-R98.

[14] XIE X B, JIN S W, WU R S. Wave equation based seismic illumination analysis [J].Geophysics,2006,71(5):S169-S177.

[15] ALKHALIFAH T. Scattering-angle based filtering of the waveform inversion gradients[J] Geophysical Journal International, 2015,200:363-373.

[16] ALKHALIFAH T, WU Z D. Multi scattering inversion for low-model wave numbers[J]. Geophysics, 2016,81(6):R417-R428.

[17] TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation [J]. Geophysics, 1984,49:1259-1266.

[18] PLESSIX RE. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications [J]. Geophysical Journal International, 2006,167(2):495-503.

[19] FICHTNER A, TRAMPERT J. Hessian kernels of seismic data functionals based upon adjoint techniques[J]. Geophysical Journal International, 2011,185(2):775-798.

[20] KÖHN D. Time domain 2D elastic full waveform tomography[D]. Kiel: Kiel University, 2011.

[21] SIRGUE L, PRATT R G. Efficient waveform inversion and imaging: a strategy for selecting temporal frequencies[J]. Geophysics, 2004,69(24):231-248.

[22] ZHOU W, BROSSIER R, OPERTO S, et al. Full waveform inversion of diving & reflected waves for velocity model building with impedance inversion based on scale separation[J].Geophysical Journal International, 2015,202(3):1535-1554.

[23] SHIPP R M, SINGH S C. Two dimensional full wavefield inversion of wide aperture marine seismic streamer data [J]. Geophysical Journal International, 2002,151:325-344.

[24] WANG F, DANIELA D, HERVÉ C, et al. Wave form inversion based on wave field decomposition[J]. Geophysics, 2016,81(6):R457-R470.

[25] YOON K, MARFURT K J. Reverse-time migration using the Poynting vector[J]. Exploration Geophysics, 2006,37(1):102-107.

[26] EDVALDO S A, REYNAM C P, ADRIANO W G S. Symplectic scheme and the Poynting vector in reverse-time migration [J].Geophysics, 2014,79(5):S163-S172.

[27] YAN Z, XIE X B. Full-wave seismic illumination and resolution analyses: a Poynting-vector-based method[J]. Geophysics,2016,81(6):S447-S458.

[28] THOMAS A D, GRAHAM A W. RTM angle gathers using Poynting vectors:SEG International Exhibition and Annual Meeting, San Antonio, October 18-23, 2011[C].Tulsa: Society of Exploration Geophysicists, 2011.

[29] JIA Y, WARREN R. Improving the stability of angle gather computation using Poynting vectors:SEG International Exhibition and Annual Meeting, Texas, September 22-27, 2013[C].Tulsa: Society of Exploration Geophysicists,2013.

[30] JIA Y, THOMAS A D. Reverse time migration angle gathers using Poynting vectors [J].Geophysics, 2016,81(6):S511-S522.

[31] TANG Y X, LEE S, ANATOLY B, et al. Tomographically enhanced full wave field inversion:SEG International Exhibition and Annual Meeting, Texas, September 22-27,2013[C].Tulsa: Society of Exploration Geophysicists,2013.

[32] ALAN R L. Fourth-order finite-difference P-SV seismograms[J]. Geophysics, 1988,53(11):1425-1436.

[33] 李娜,李振春,黄建平,等.Lebedev网格与标准交错网格耦合机制下的复杂各向异性正演模拟[J].石油地球物理勘探,2014,49(1):121-131.

LI Na, LI Zhenchun, HUANG Jianping, et al. Numerical simulation with coupling Lebedev and standard staggered grid schemes for complex anisotropic media[J]. Oil Geophysical Prospecting, 2014,49(1):121-131.

[34] 黄建平,杨宇,李振春,等.基于 M-PML 边界的Lebedev网格起伏地表正演模拟方法及稳定性分析[J].中国石油大学学报(自然科学版),2016,40(4):47-56.

HUANG Jianping, YANG Yu, LI Zhenchun, et al. Lebedev grid finite difference modeling for irregular free surface and stability analysis based on M-PML boundary condition[J]. Journal of China University of Petroleum (Edition of Natural Science),2016,40(4):47-56.

[35] 李振春,雍鹏,黄建平,等.基于矢量波场分离弹性波逆时偏移成像[J].中国石油大学学报(自然科学版),2016,40(1):42-48.

LI Zhenchun, YONG Peng, HUANG Jianping, et al. Elastic wave reverse time migration based on vector wave field seperation[J]. Journal of China University of Petroleum(Edition of Natural Science), 2016,40(1):42-48.