基于HMOPSO的数控切削参数优化模型的建立与仿真

郭婷

（西安职业技术学院陕西西安710032）

数控技术是当前机械自动化生产加工的核心部分，通过数控技术工作人员能够对机器进行编程控制，从而使机器按照既定的程序进行机械零部件的生产和加工。在数控机床加工生产零部件的过程中，选择不同的切削参数会影响其生产率和成本。因此，合理选择切削参数能够大幅提升生产率，且降低生产成本。然而，目前大多数工厂对于切削参数的确定仅依靠工人个人经验或者参考手册，难以实现切削参数最优化选择。随着数值优化计算方法、数学建模等方法的不断发展，通过数学建模及优化算法来求解模型最优化参数成为了新的研究方向。在此前，人们已经通过数学建模对数控切削参数优化进行了研究[1-5]。然而此前研究中大部分模型参数的取值依靠经验参数，使得优化结果不够精确；或是只针对成本而未对加工效率进行研究[6]。

为此，文中对数控切削参数优化进行了研究。并结合实际机床和道具的约束，建立了一个以最大生产率及最低生产成本为优化目标的数学模型。同时，采用混合多目标粒子群优化算法对该数学模型进行最优化求解。最后，通过实例仿真对该模型进行验证。

1 数控切削多目标优化模型

1.1 多目标优化问题

在工程项目中，一个项目通常具有多项指标参数。而衡量一个项目最终结果的优劣，就是看这些指标参数最终达到的水准。对于工程项目人员而言，寄希望于项目的各项指标均可达标。比如工厂生产一台机器，既希望生产出的机器性能优异、能耗低、稳定性高且生产成本低，这就涉及到一个多目标最优化问题。所谓的多目标优化问题指的是，在同个约束空间内同时对目标函数的几个参数进行优化。多目标优化问题可以描述为以下的数学模型：

式中，J和K分别代表不定式与等式约束的个数。为决策变量空间，而候选解为x=(x1,···,xn)∈ Ω 。

对于a0,b0∈ℝn，若同时满足：

1）fi(a0)≤fi(b0)；

2）a0≤b0

则称a0支配b0。多目标优化问题就是产生一组互不支配的最优解集，其被定义为Pareto非支配集。

1.2 参数设定

对于数控切削而言，其主要考虑3个参数对切削效果的影响。即切削速度v、进给量f以及切削深度ap。对于切削深度，由于其对刀具的磨损相较于切削速度和进给量小，且可根据零部件的具体加工要求确定。因此，文中将切削深度当为已知量，仅对切削速度及进给量参数进行优化。

1.3 目标函数设定

对于数控粗加工而言，其最主要的影响因素是生产效率和成本。因而文中将优化问题集中在生产效率和成本上，即如何通过优化参数实现最高的生产效率以及最低的生产成本。对于一次批量生产，一次完整的零部件加工过程所需耗费的工时为[7]：

其中，Ts为工人安装刀具所花费的时间；Tm为零部件进行切削所花费的时间；Th为所有工序换刀的平均耗费时间；Ti为切削机器空转所用的时间。

对于Tm，其可表示为：

其中，V为零部件切削的面积；v为切削速度；f为进给量；ap为切削深度。则Th可表示为：

其中，Tc为换刀时间；CV，kV，xV，yV，m为刀具耐磨系数。

对于一次批量生产，一次完整的零部件加工过程所需耗费的成本为：

其中，Ct为购买刀具成所花费的成本；C1为单位时间工人工作所消耗的人力成本；C0为单位时间管理所耗费的成本。由于同时对两个目标，即对切削速度和进给量同时进行优化是不现实的。为此，本文定义了一个协调系数λ。将多目标优化问题转变为单目标优化问题，如下式所示：

当λ=1时，式（6）转变为式（5）。此时，最低生产成本为目标函数的优化目标；

当λ=0时，式（6）转变为：

此时，最高生产效率为目标函数的优化目标。

当0<λ<1时，此时目标函数以最高生产效率以及最低生产成本为优化目标。

1.4 约束条件设定

在对优化函数进行求解之前，需根据机床的实际运行状态对一些参数进行约束，使得优化问题符合实际情况[8-9]。

1）对于切削速度，其必须满足机床主轴最大和最小转速约束：

其中，Nmax和Nmin分别为机床主轴转速的最大值与最小值；D为零部件的直径。

2）对于给进量，其应满足机床最大进给量和最小进给量的约束，即：

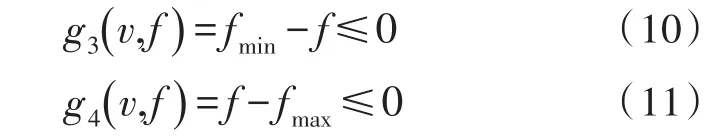
其中，fmax和fmin分别为机床进给量最大值与最小值。

3）切削进给力要满足机床最大进给力约束，即：

其中，Fmax为机床最大进给力；为切削力参数。

4）零部件切削功率必须满足机床最大功率约束，即：

其中，Pmax为机床最大功率；η为机床有效系数。

2 优化算法

2.1 多目标粒子群优化算法

多目标粒子群优化（MOPSO）算法是在Pareto优胜关系的基础上，来对多目标优化问题进行最优解求解的一种算法。其收敛速度及寻找最优解速度快，因而受到众多研究者的青睐[10]。在多目标粒子群优化算法中，粒子通过利用体极值点以及全局最优解来更新自己。体极值点文中用Pbest表示，全局最优解用Gbest表示。粒子的速度和位置更新，可由式（14）和式（15）决定：

多目标粒子群优化算法流程，如图1所示。首先，输入各个系数的数值并计算相应的参数值；然后，初始化满足所有约束条件的粒子群；接着计算粒子的目标函数值，并选取个体极值点以及全局最优解来确定更新后的速度与位置；同时判断是否达到最大迭代次数，若是即输出最优解；若不是则返回重新计算目标函数数值及个体极值点，得到全局最优解。再重新计算粒子更新后的速度和位置，直至达到最大迭代次数，输出最后的最优解。

图1 多目标粒子群优化算法流程

2.2 模拟退火算法

模拟退火法是由N.Metropolis于1953年提出的一种以概率为基础的算法，其模仿固体退火过程。即先将固体用高温加热，然后再让其逐渐冷却。固体加热时，其内部粒子能量增大而变得无序。再降温冷却后粒子趋向有序，能力减少。模拟退火算法通过在搜索过程中以一个极其小的概率，使局部最优解跳出而搜索附近的次优解。从而避免了算法最优陷入局部最优解的境地，最终能够得到全局最优解。但模拟退火算法若要得到全局最优解，则需要在初始退火温度足够高、而终止退火温度足够低的条件下才能实现[11-15]。

2.3 混合多目标粒子群算法

采用多目标粒子群算法求解多目标最优化问题时，其容易陷入局部最优解。因而在某些约束条件下，无法满足最优化问题求解目的，即无法得到全局最优解。而模拟退火算法能够避免算法陷入局部最优解，而求解得到全局最优解。因此，将多目标粒子群算法跟模拟退火算法相结合，即结合两者的优点。从而使收敛速度与求解速度更快，同时能够避免陷入局部最优解而得到全局最优解。

本文在多目标粒子群算法中两次采用模拟退火算法，其使用方式如下所示：

1）在确定个体极值点时，采用模拟退火算法进行搜索计算。由于算法初始温度较高，故能够增大劣解被选中的几率。从而扩大了搜索范围，避免了算法陷入局部最优解。

2）在确定全局最优解时，采用模拟退火算法进行搜索计算，避免迭代过程中种群粒子趋向局部最优解，增大算法搜索的分散性。混合多目标粒子群优化算法流程，如图2所示。

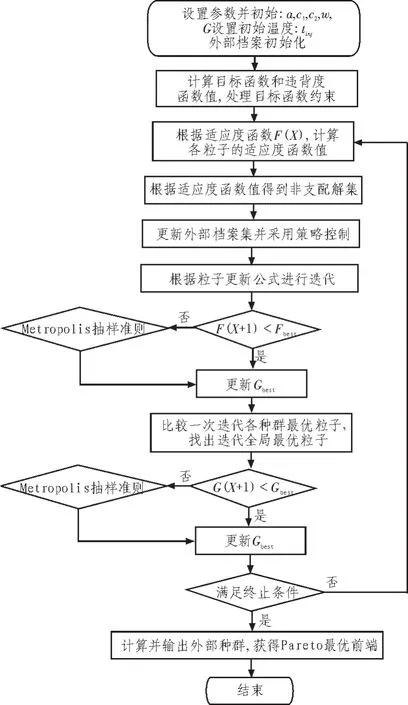
图2 混合多目标粒子群算法

3 模型仿真

3.1 参数确定

数控机床参数，如表1所示。

表1 数控机床参数

查阅相关切削手册，可得刀具耐磨系数为：Cv=189.8，xv=0.15，yv=0.20，m=0.20，kv=1.0，而切削力系数为：。

文献[16]，确定成本参数为：Ct=60元C1+C0=2.39元/min。时间参数为Ts=0.12min，Tc=2.39min，Ti=0.1min。

3.2 模型仿真

设定粒子群大小为20，迭代次数最大为150，惩罚因子为100。粒子群算法求解最优化问题过程，如图3所示。从最初的分散到最后粒子群趋向于某个范围，当迭代次数为150时，得到了最优结果。其优化结果，如表2所示。

图3 粒子群求解过程

表2 优化结果

如图4所示为不同算法下所对应的Pareto图。从图中可看出，通过HMOPSO算法得到的Pareto前沿解效果更优。而在相同条件下，其能够搜索得到对于成本以及加工时间之间相对平衡的最优结果。

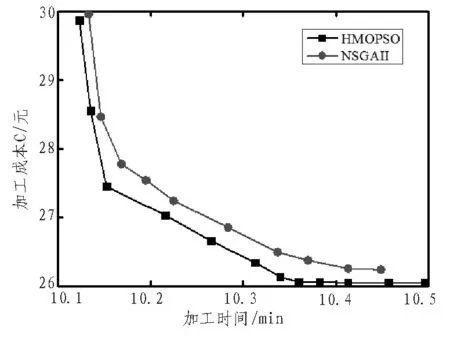
图4 不同算法下的Pareto图

4 结束语

数控技术是当前机械自动化生产加工的核心部分，选择不同的切削参数会影响数控切削的生产率和成本。因此，目前大多数工厂对于切削参数的确定仅依靠工人个人经验或者参考手册，难以实现切削参数最优化选择。因此，本文对数控切削参数优化进行了研究，结合实际机床和道具的约束建立了一个以最大生产率与最低生产成本为优化目标的数学模型。同时，采用混合多目标粒子群优化算法对该数学模型进行最优化求解。最后，通过实例仿真对该模型进行验证。

参考文献：

[1]黄拯滔，杨杰，张超勇，等.面向能耗的数控铣削过程建模与参数优化[J].中国机械工程，2016，27（18）:2524-2532.

[2]刘娟桂.高效低碳数控加工参数多目标优化模型研究[J].电子技术与软件工程，2016（11）:156-157.

[3]张楚锋，梁祖欣.基于遗传算法的数控铣床切削参数优化[J].机电工程技术，2016（1）:85-87.

[4]辛燕.数控车床切削参数优化研究[D].昆明:昆明理工大学，2016.

[5]王仁伟，何玲，邵芳.环槽车削加工工艺参数优化[J].组合机床与自动化加工技术，2016（11）:112-114.

[6]赵静，李丽，王国勋.基于粒子群算法的加工参数多目标优化技术研究[J].机械制造，2014，52（11）:42-46.

[7]黄如林，刘新佳，汪群.切削加工简明实用手册[M].北京:化学工业出版社，2010.

[8]Wang Y，Cai Z.Combining Multiobjective Optimi⁃zation With Differential Evolution to Solve Con⁃strained Optimization Problems[J].IEEE Transac⁃tions on Evolutionary Computation，2012，16（1）:117-134.

[9]Liu J，Teo K L，Wang X，et al.An exact penalty function-based differential search algorithm for constrained global optimization[J].Soft Comput⁃ing，2016，20（4）:1305-1313.

[10]Singh M R，Singh M，Mahapatra S S，et al.Parti⁃cle swarm optimization algorithm embedded with maximum deviation theory for solving multi-objec⁃tive flexible job shop scheduling problem[J].Inter⁃national Journal of Advanced Manufacturing Tech⁃nology，2016，85（9-12）:2353-2366.

[11]陶俐言，杨海斌.基于改进引力搜索算法的公差多目标优化设计[J].机械设计与研究，2017（2）:133-137.

[12]张秀芬，王磊.复杂产品多粒度再制造性综合评价方法[J].制造技术与机床，2016（1）:78-82.

[13]方欣欣，龚如宾，李大为.基于余弦距离的多目标粒子群优化算法[J].电子科技，2016，29（3）:48-52.

[14]胡艳娟，王义强，王尧，等.基于改进粒子群算法的加工方案多目标优化[J].沈阳工业大学学报，2011（4）:394-399.

[15]董旭良，王建华.一种求解多目标优化问题的粒子群算法的研究[J].电子设计工程，2013，21（3）:36-39.

[16]Liang Ming，Tet Yeap，Saeed Rahmati，et al.Fuzzy control of spindle power in end milling pro⁃cesses[J].International Journal of Machine Tools&Manu ，2002（42）:1487.