基于一致性的无人机编队形成与防碰撞研究

秦文静，林勇，戚国庆

（南京理工大学自动化学院，江苏南京210094）

无人机编队控制是无人机协同控制领域一项重大基础研究课题，引起了国内外诸多研究人员的兴趣[1]。无人机编队控制方法[2-5]主要包括领航跟随法、虚拟结构法、基于行为法和图论法。在无人机编队形成的研究方面，国内外学者已取得一些成果。文献[6]利用势场方法来模拟群聚集行为和凝聚力。文献[7]利用粒子滤波方法使各机跟踪编队几何中心，实现了集结的渐近稳定。文献[8]尝试通过基于行为法来模拟群集行为，以实现编队的智能集结和优化控制。文献[9]研究了小型四旋翼无人机机群自主编队形成，在串级控制系统框架下提出一种基于Hamilton环的通信拓扑设计方案。传统研究无人机编队的方法常常将无人机视为质点目标，鲜有考虑编队形成过程中，无人机间的防碰撞问题。

综上可见四旋翼无人机编队形成过程中机间防碰撞的问题仍是一个值得深入研究的课题。针对该问题，本文将图论法与领航跟随法相结合，在所有跟随者能够获得领航者状态信息的通信拓扑结构下，将四旋翼无人机的动力模型描述为二阶积分器动力系统，利用二阶一致性算法获得编队形成的轨迹，并借助四旋翼无人机可悬停的特点，通过调整集结点高度，避免无人机在编队形成过程中发生碰撞。

1 编队形成算法

1.1 一致性算法

所谓一致性是指随着时间的演化，如果网络中每个节点的值或状态趋于一样[10]，我们就称采用这种协议或者算法的网络能够实现一致，一致性算法表征四旋翼无人机之间信息传递的规则[14]。根据文献[11，15]当系统拓扑结构中包含有向生成树时，系统能够到达一致。本文在固定连通拓扑G下研究编队形成控制方法，领航者向外广播自身的状态信息位置和速度，其余跟随者接收来自领航者的信息，跟随者之间的拓扑关系是任意的。

为使四旋翼无人机控制作用更准确有效，将其动力学模型描述为二阶积分器动力系统，

si和vi是第i个的位置和速度信息；控制变量ui=（uix，uiy，uiz），uiy、uiz分别对应俯仰、横滚方向的控制力矩，uiz对应驱动无人机位姿变化的4个螺旋桨产生的总的升力T。

本文给出以下一致性算法：

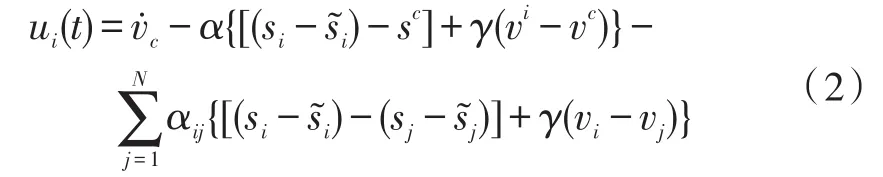
式中，sc和vc是领航者位置和速度信息，是集结点相对位置偏差；若节点j能接收i的状态信息，αij=1，α=1。γ值见文献[1]。经过一段时间后，‖si-sj‖→0且‖vi-vi‖→0，此时编队达到或者达成一致。

1.2 编队形成控制策略

编队形成具体步骤如下：

Step1.确定参考集结点：定义编队中心为ρc=(xc,yc,zc)，即编队协同变量。定义相对位置偏差i，定义无人机i当前位置测量值ρi，关系为ρi-i=pc。Step2.计算飞行轨迹：利用二阶一致性算法计算无人机编队形成的飞行轨迹。Step3.获得最短分离距离dmin,ij：第i、j个无人机安全半径分别为Ri和Rj。设已求得无人机路径同一时刻的离散点k的坐标分别为（xi,k，yi,k，zi,k）和（xj,k，yj,k，zj,k），避免碰撞的条件表示为[16]：

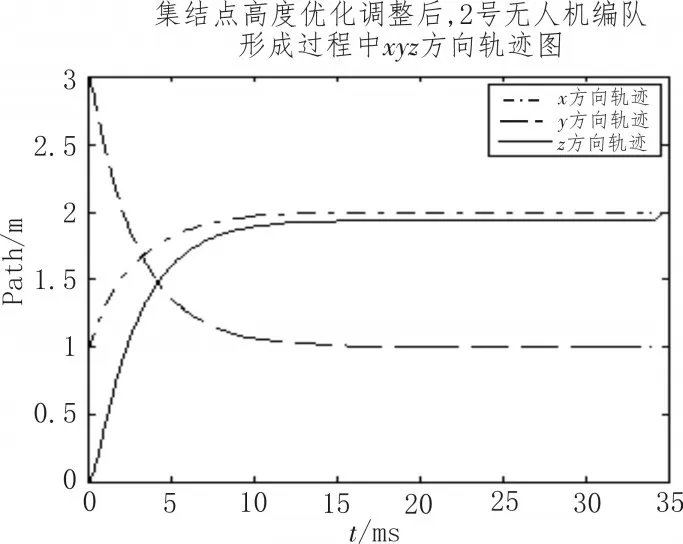
Step4.判断dmin>Ri+Rj是否成立，不成立进入Step5；成立则进入Step6。Step5.调整集结点高度hi：例如有对无人机，有m对有碰撞的可能，例举出相应的控制策略。调整hi的规律是，若满足i

2 数值仿真

设置四旋翼编队规模N=5，1号为领航者，2～5分别为跟随者，通信拓扑结构为图1。

图1 各无人机之间通信拓扑结构G′

仿真参数设置如下（文中距离与实际距离之比为1:5，文中距离单位为m）：

1）具体参数为α=1，αij=1，γ=2，安全距离Ri、Rj=0.05 m，每次调整高度Δhe=0.1 m。2）领航者始终悬停在（2 m，2 m，2 m），跟随者的初始位置为满足不碰撞条件的随机位置。3）跟随者集结点的相对位置偏差为。为了满足防碰撞的条件，调整集结点高度偏差为ΔhiT。

例如跟随者初始位置为，计算得到跟随者之间最短分离距离Dmin,ij=[1.384 2，0.392 8，0.007 7，1.414 2，1，0.445]，i，j=2～5。dmin,25=0.007 7m<0.1m，调整偏差 Δh2T=0.062 9，Δh5T=-0.062 9，其余高度偏差为0，得到最短分离距离为0.394 7，0.1，1.414 2，1，0.448 9]。可以看出dmin,ij≥0.1 m。如图2所示，2号飞到（2 m，1 m，1.937 1 m）以后，立即垂直上升到原集结点（2 m，1 m，2 m）。如图3所示，以2号、5号无人机最短分离距离点为球心，半径为0.05 m两个球体相切，说明这两架没有发生碰撞的可能。由此说明通过调整集结点高度，能够实现无人机在编队形成过程中避免碰撞。

图2 2号xyz方向的轨迹图

图3 2、5号轨迹最短距离处半径0.05m的球体

图4 无人机编队形成过程的三维轨迹图

3 结 论

本文针对四旋翼无人机编队形成过程中防碰撞的问题，将四旋翼无人机的动力学模型描述为二阶积分器动力系统，结合领航跟随法和图论法，利用二阶一致性算法获得编队形成的轨迹，通过优化调整集结点高度使得无人机编队形成的轨迹满足不发生碰撞的条件，并通过Matlab仿真验证了该控制策略的有效性。有关多无人机编队协同控制的工程实现问题，将在后续研究中进行。

参考文献：

[1]李磊，李小民，郑忠贵，等.基于一致性理论的四旋翼无人机分布式编队控制方法[J].电光与控制，2015（10）：19-23.

[2]Sisto M，Gu D.A Fuzzy Leader-Follower Ap⁃proach to formation control of multiple mobile ro⁃bots[C]//Ieee/rsj International Conference on Intelli⁃gent Robots and Systems.IEEE，2006:2515-2520.

[3]郑秀娟，吴怀宇，程磊，等.多机器人主—从行星式编队控制[J].信息与控制，2012，41（3）:370-377.

[4]Askari A，Mortazavi M，Talebi H A.UAV forma⁃tion control via the virtual structure approach[J].Journal of Aerospace Engineering，2015，28（1）:04014047.

[5]王祥科，李迅，郑志强.多智能体系统编队控制相关问题研究综述[J].控制与决策，2013，28（11）:1601-1613.

[6]Gazi V，Passino K M.Stability analysis of swarm[J].IEEE Transactions on Automatic Control，2003，48（4）：692-697.

[7]Easthope P F.Tracking simulated UAV sward using particle filters[C]//IET Conference on Data Fusion and Target Tracking 2014；Algorithms and Applica⁃tion，2014（4）:1-6.

[8]Reynold C W.Flock，herds，and schools:A distribut⁃ed behavior model[C]//Proceedings of SIGGRAPH.New York:ACM，1987.

[9]邢关生，杜春燕，宗群，等.基于一致性的小型四旋翼机群自主编队分布式运动规划[J].控制与决策，2014，29（11）:2081-2084.

[10]吴治海.网络环境下的多智能体系统一致性问题研究[D].武汉：华中科技大学，2011.

[11]Ren W，Beard R W.Consensus seeking in multia⁃gent systems under dynamically changing interac⁃tion topologies[J].IEEE Transactions on Automatic Control，2005，50（5）:655-661.

[12]王祥科，李迅，郑志强.多智能体系统编队控制相关问题研究综述[J].控制与决策，2013（11）:1601-1613.

[13]李向舜.网络化群体系统编队与一致性控制[D].武汉：华中科技大学，2009.

[14]朱旭，张逊逊，尤谨语，等.基于信息一致性的无人机紧密编队集结控制[J].航空学报，2015，36（12）:3919-3929.

[15]OLFATI-SABER R FAX J A，Murray R M.Consensus and cooperation in networked multiagent system[C]//Proceedings of the IEEE.2007:215-233.

[16]邵壮，周洲，王彦雄，等.基于CPSO的UAV编队集结路径规划[J].飞行力学，2017，35（1）:61-65.