韦伯-费希纳模型在湖泊(水库)预警评价中的应用

2018-05-17林秀珠饶清华欧晓敏

水土保持通报 2018年2期

林秀珠, 饶清华, 欧晓敏

〔近海流域环境测控治理福建省高校重点实验室(福建师范大学福清分校), 福建福清 350300〕

近年来，随着中国社会经济发展与人口增长，湖泊(水库)水环境功能呈现降低趋势[1]。湖泊(水库)作为人类重要的生活饮用水水源，人类生产生活活动过程会对水源产生一定程度的污染。由于湖泊(水库)往往承担了生活饮用水水源地的功能，改善湖泊(水库)的水质状况是一项长期而艰巨的任务，因此，构建湖泊(水库)预警评价指标体系并进行水质预警评价就显得十分必要。国内外的学者们[2-7]对其进行了深入的研究，提出相关的湖泊(水库)水质评价模型，如：单因子评价法、模糊数学评价法、灰色聚类法、物元分析法、层次分析法、人工神经网络评价法等。韦伯—费希纳模型(Weber-Fechner’s Model，简称W-F模型)来源于19世纪中期，由费希纳创始的心理物理学派实践推导而来，能准确的表达人体的反应量k与客观环境刺激量c之间的函数关系，起初被应用于声学和心理学领域[8]。李祚泳等[9]最早将韦伯—费希纳定律应用于空气环境质量评价中，薛文博等[10]首次将韦伯—费希纳模型转化成环境质量评价模型，拓展了韦伯—费希纳模型的应用领域。目前，韦伯—费希纳模型已用于生态环境质量、湖泊(水库)富营养化以及水环境预警评价方面的研究中[11-16]。与已有的研究方法相比，该模型具有计算过程简单、科学合理、直观清晰等特点。

湖泊(水库)水质预警评价的本质就是根据水环境质量的要求，建立水质预警指标体系和安全等级标准，将水质评价指标从高维空间映射到低维空间，转换成一维实数的水质综合预警评估指数，并且在映射过程中能够反映原高维空间中水质指标的分类信息和排序信息，然后对各评价对象的水质预警等级进行综合评估。如何确定这些水质指标的权重是湖泊(水库)水质预警评价的难点之一，采用客观赋权法进行赋权，避免了各指标权重确定的人为干扰，减少了主观随意性，使评价指标赋权更科学、合理。此外，已有的研究主要存在所选的评价指标不能完全反映湖泊(水库)水质预警的本质，很少将溶解氧(dissolved oxygen, DO)作为水质预警评价的指标以及评价年限不完整，时间跨度不长，不能体现评价对象的水环境质量变化情况等不足。因此，本研究将W-F模型用于湖泊(水库)水环境预警评价，并以福建省的莆田东圳水库、福清东张水库、三明东牙溪水库2010—2016年水质为例，对各水库进行综合评价，旨在为湖泊(水库)水环境预警评价提供一种过程简单、直观清晰、便于推广、结果科学合理的评价方法。

1 研究方法

1.1 韦伯-费希纳模型基本原理

W-F模型基本表达式为：

k=αlgc

(1)

式中：k——人体产生的反应量；c——外界环境刺激量；α——韦伯常数。

W-F模型应用于湖泊(水库)水质评价中，基于以下3点假设： ①将外界刺激量c视为水库中某种水质指标的浓度； ②将人体反应量k视为该种指标对人体影响程度； ③韦伯常数α是由该水质指标性质所决定的，对于同一指标α为常数，而在湖泊(水库)水质预警评价中往往涉及到多个水质指标，因此可把α视为各水质指标的权重[11,14]。

基于以上3条假设，W-F模型关系式可表示为：

kij=αijlg(cij+1)

(2)

式中：kij——第i个监测点第j个水质指标的污染对人体的危害程度；αij——第i个监测点第j个水质指标的权重；cij——第i个监测点第j个水质指标监测浓度的标准化值；cij+1的目的是使lg(cij+1)>0，可以通过数学证明不影响评价结果[14]。

1.2 确定指标权重和综合影响指数ki值

1.2.1 确定指标权重湖泊(水库)水质预警评价问题是一个典型的多目标、多决策的复合系统问题，在进行湖泊(水库)水质预警评价时，确定指标权重显得尤为重要，关系到评价结果的准确性。确定权重的方法一般分为主观和客观赋权法2种。由于不能充分考虑各指标提供的信息量，主观赋权法确定的权重往往缺乏客观依据，会导致某一指标的权重存在过高或过低的可能，使评价结果不能完全反映客观实际情况。采用变异系数法来确定各湖泊(水库)的水质指标权重，通过水质指标变异系数之间的大小关系来确定指标个体差异的显著性，如果其变异系数越大则差异也就越显著，以此作为确定评价指标权重的依据。该方法可以根据水质指标间的差异程度，客观确定指标的权重，消除水质指标权重计算时的人为干扰，使水质指标的权重确定更科学、合理，评价结果更符合实际。计算步骤如下[15]。

(1) 将湖泊(水库)各水质指标监测数据进行标准化，消除量纲影响。

(3)

式中：cij′——第i个监测点第j个水质指标的监测浓度值；cij——第i个监测点第j个水质指标的监测浓度标准化值；cj——第j个水质指标在分级标准中的最高浓度值。

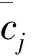
(4)

(5)

(3) 求出各指标的变异系数θj。

(6)

(4) 确定第j项指标权重αj。

(7)

1.2.2 确定综合影响指数ki值ki值的计算公式为：

(8)

式中：ki——第i个湖泊(水库)监测点水环境的综合影响指数。

通过各水库水环境综合影响指数ki值与对应的地表水环境质量标准(GB3838-2002)标准化所得到综合影响指数值对比，来确定湖泊(水库)水环境质量等级与综合影响指数间关系，最后确定湖泊(水库)水环境预警等级。根据W-F模型的构建可知，该模型具有以下特点：首先，该模型是在对水质指标污染浓度的基础上推导出来的，因此，能够定量描述湖泊(水库)水环境质量的感觉强度变化关系，反映湖泊(水库)水环境质量变化的影响，并能够实现评价对象指标间的纵向以及横向比较；其次，通过建立评价矩阵，该模型能够实现高维空间到低维空间的映射，并且在映射过程中能够反映原高维空间中水质指标的分类信息和排序信息；最后，权重的确定采取了客观赋权的“变异系数法”，根据各评价指标间的差异程度来计算权重，克服了人为的干扰，使权重确定更科学、合理。

2 实例研究

2.1 研究对象概况

福建省莆田东圳水库、福清东张水库、三明东牙溪水库分别是各自地区主要的饮用水水源，同时也是福建省省控水源地监测区。因此，本研究以莆田东圳水库、福清东张水库、三明东牙溪水库2010—2016年水质为例，对各水库进行水环境预警评价，对于科学合理判断水库水质预警等级，拓展评价模型的应用范围，具有重要意义。水库水质数据来源于福建省环境保护厅。

2.2 确定评价指标权重

各水库中DO，CODMn，TP，NH3-N，TN等评价指标的初始数据，以每季度表示，其中该污染指标选取表1中第Ⅴ类水质标准值(由于DO为反向指标，选取Ⅰ类水质标准值)，根据公式(3)进行标准化，再由公式(5)—(7)计算出各因子的权重，求得权重分别为0.051 8，0.111 0，0.257 8，0.490 2，0.089 1。

表1 地表水环境质量标准限值 mg/L

2.3 确定ki值

参考地表水环境质量标准，根据公式(2)和(8) 求得综合影响指数ki值，建立ki值与预警等级之间关系，具体详见表2。由表2可知，ki<0.046 2时预警等级为无警，0.046 2≤ki<0.094 0时为轻警，0.094 0≤ki<0.154 7为中警，0.154 7≤ki<0.218 4为中重警，0.218 4≤ki<0.263 9为重警，ki≥0.263 9为超重警。2010—2016年福建省莆田东圳水库、福清东张水库、三明东牙溪水库各指标监测溶度季度平均值与综合影响指数ki值详见表3—5。

表2 综合影响指数ki值及预警等级

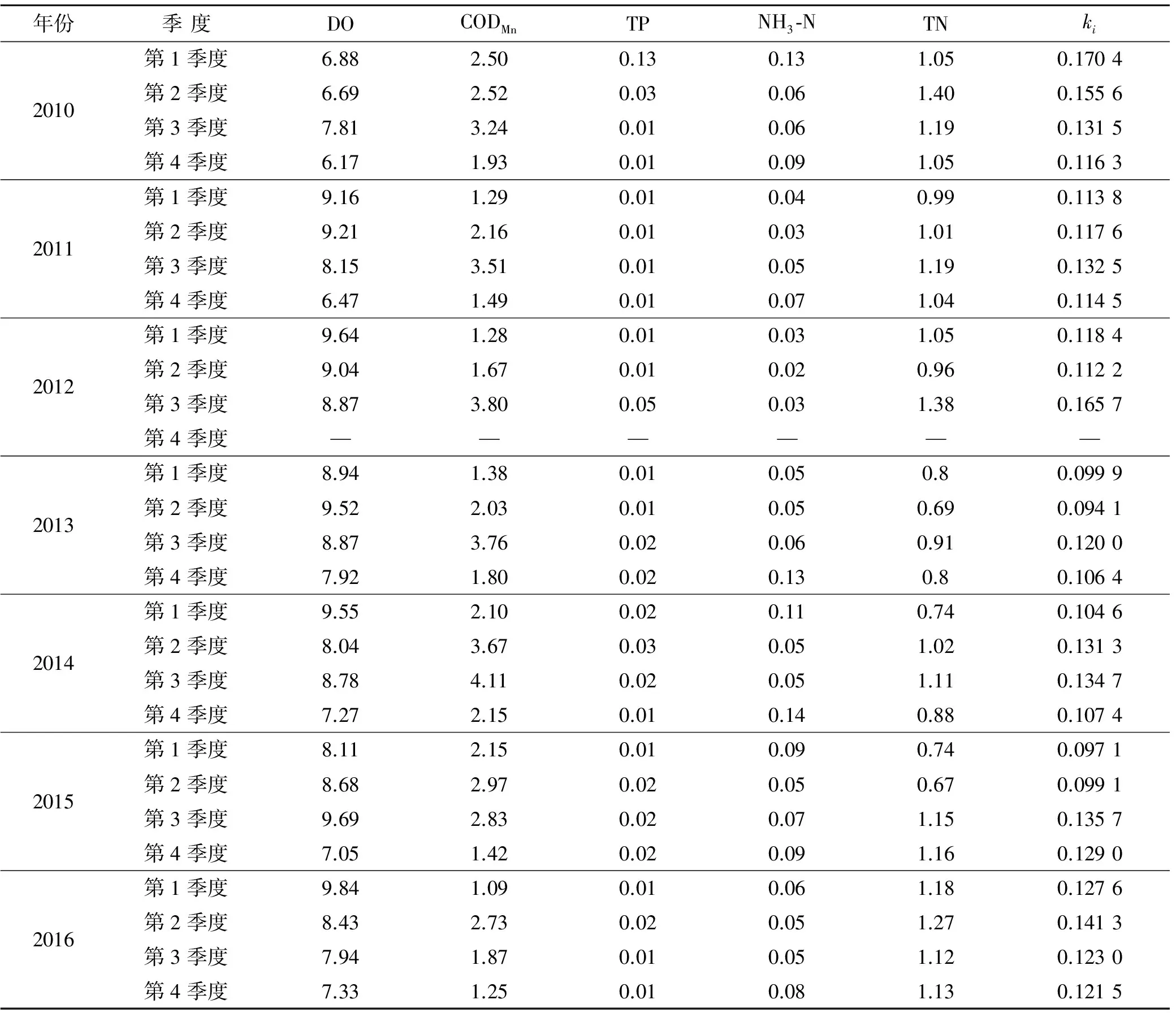
表3 莆田东圳水库监测各指标2010-2016年季度平均值与ki值 mg/L

注：“—”表示数据缺失。下同。

3 结果与分析

由表2—5的综合影响指数ki值以及对应的预警等级可得出最终的评价结果，具体详见表6。

(1) 莆田东圳水库。莆田东圳水库的综合影响指数ki值范围为[0.094 1，0.170 4]，除了2010年第1，2季度，2012年第3季度处于中重警外，其余的季度中警，说明其预警等级应为中警—中重警。总氮和总磷浓度偏高是水质预警为中警—中重警的主要原因。东圳水库具有发电、防洪、灌溉、养殖、游览等作用。是莆田市唯一的一座大型水库，也是福建省大型水库之一，是莆田市的生命线工程和“大水缸”。近年来，东圳水库周边区域的经济不断发展，虽然该区域没有引入污染型工业企业，但是随着该区域周边居民生活水平的提升，产生的生活污染强度加大，这是导致水库总氮、总磷偏高的一个重要原因；此外，随着东圳水库旅游开发力度的加大，旅游的人数在不断增加，对水库的水质也造成潜在的影响。为了从根本上解决水库水质安全问题，2010年以来，莆田市开始实施东圳水库水源地综合治理，以“大坝安全、水质优良、环境优美”为目标，主要包括水源地一级保护区征地、搬迁、安置工程，分层取水工程，村庄污水治理、生态林建设工程，流域河流治理工程，库滨带生态修复工程等工程。因此，总体上看，东圳水库水环境质量呈现改善的趋势。

(2) 福清东张水库。福清东张水库的综合影响指数ki值范围为[0.080 4，0.158 9]，除了2013年第3季度为轻警，2012年第1季度处于中重警外，其余的季度中警，因此，预警等级为中警。东张水库是福清市最大的饮用水水源地，但结合表4可知，水库存在总氮、总磷浓度偏高的问题。造成东张水库总氮、总磷偏高的主要原因是入库溪流周边乡村排放的生活污水和养殖废水。虽然福清市加大了水库周边区域养殖场的整治，基本杜绝了养殖废水的排放，但东张镇区产生的生活污水仍然处于直排状态。此外，东张水库周边区域农业面源污染也是导致水库总氮、总磷偏高的原因之一，尤其是在雨季，随着雨水冲刷，地表污染物就随着径流汇入水库。为了进一步保护东张水库水质，应尽快完善截污工程，解决库区周边区域污染物及垃圾堆放问题，以便减轻东张水库外源污染的负荷量；加大上游地区养殖场的整治力度，防止重建或扩建；加大水源保护投入，建立库区生态农业示范试点，提高库区居民水源保护积极性。

(3) 三明东牙溪水库。三明东牙溪水库的综合影响指数ki值范围为[0.078 5，0.130 7]，其中，2010年第4季度、2011第3季度、2012年第3季度、2013第3,4季度为轻警外，其余季度为中警，该水库2010—2016年的水体水质处于相对平稳的状态。

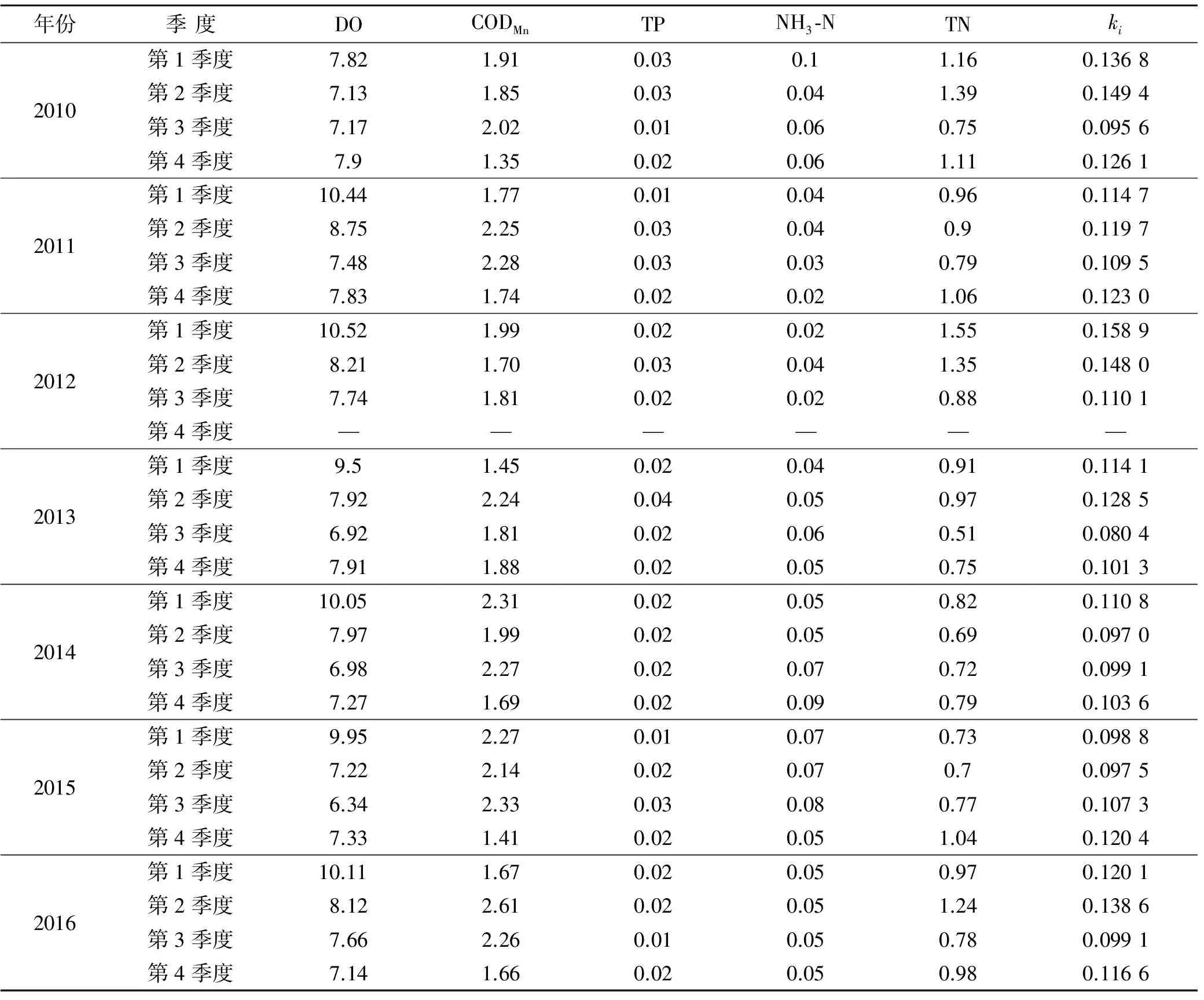
表4 福清东张水库监测各指标2010-2016年季度平均值与ki值 mg/L

结合表5可知，水库总氮浓度偏高是水质发生变化的主要原因。东牙溪水库是三明市区目前唯一的生活饮用水源地，水库汇水区内主要的污染源为生活污水、养殖废水、笋干加工制作废水、农业面源污染等，特别是近年来，由于保护区内村民的生产和生活，导致东牙溪沿河两岸植被破坏，致使水土流失日益加重，从而加重了库区水质的污染负荷。因此，应严格禁止水库保护区内从事可能污染水源地的违法行为，加大水库周边区域生活垃圾及污水的处理力度，加快实施水库保护区林业建设，加强东牙溪河岸植被的保护，增强水源涵养能力；加大推进农业生产方式转变力度，降低各类农业污染物产生量，尤其是要引导水库保护区周边区域农民减少化肥使用量；加大东牙溪水库水源地保护投入，建立水源地保护生态补偿机制。

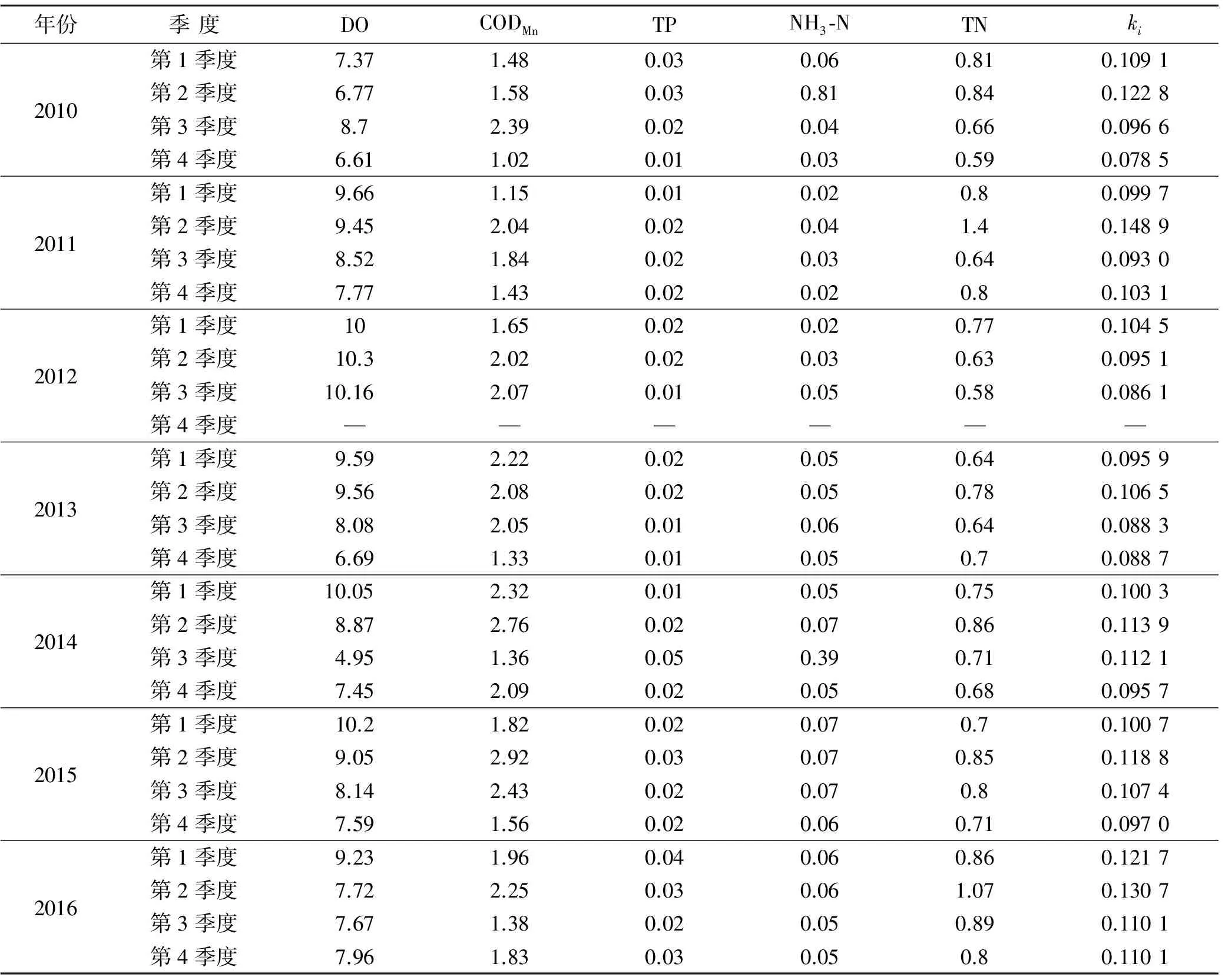
表5 三明东牙溪水库监测各指标2010-2016年季度平均值与ki值 mg/L

表6 W-F法评价结果

4 结论

(1) 以莆田东圳水库、福清东张水库、三明东牙溪水库2010—2016年水质为例，应用W-F模型，对各水库进行水环境预警评价，确定水库水质预警等级，拓展W-F模型的应用范围。由评价结果可知，上述3个水库水质总体上预警等级为中警。

(2) W-F模型既有单项指标又有综合指标，能够实现评价对象指标间的纵向以及横向比较；能够定量描述湖泊(水库)水环境质量的感觉强度变化关系，反映湖泊(水库)水环境质量变化的影响；与传统简单加权法相比，通过指标之间的差异程度来确定权重，减少了主观随意性；模型具有计算过程简单、评价精度高、应用性强等优点，为湖泊(水库)水质预警等级综合评价提供了新方法，拓展评价模型的应用范围；评价结果不但可以明确湖泊(水库)水质预警等级及其在时间上的差异，还能体现湖泊(水库)水环境中薄弱的环节，便于将评价指标与结果之间进行时空相关性分析，在湖泊(水库)水质预警等级评价问题中具有一定的应用价值。

[参考文献]

[1] 杨桂山,马荣华,张路,等.中国湖泊现状及面临的重大问题与保护策略.湖泊科学,2010,22(6):799-810.

[2] 徐祖信.我国河流单因子水质标识指数评价方法研究[J].同济大学学报:自然科学版,2005,33(3):321-325.

[3] 邬敏,李祚泳,刘智勇,等.一种改进的集对分析法在湖泊富营养评价中的应用[J].水资源保护,2009,25(2):5-9.

[4] 饶清华,张江山.熵权物元分析模型在湖泊富营养化评价中的应用[J].环境工程,2006,24(6):80-82.

[5] Shen Jian. Optimal estimation of parameters for a estuarine eutrophication model[J]. Ecological Modelling, 2006,191(3):521-537.

[6] 孔健健,张江山.属性识别理论模型在湖泊水质富营养化评价中的应用[J].环境工程,2004,22(5):66-68.

[7] 张晓丹,黄朝君,徐菡,等.基于RBF神经网络的湖库水质富营养化程度评价模型[J].环境工程,2007,25(2):80-82.

[8] Drösler J. An n-dimensional Weber law and the corresponding Fechner law[J]. Journal of Mathematical Psychology, 2000,44(2):330-335.

[9] 李祚泳,彭荔红.基于韦伯—费希纳拓广定律的环境空气质量标准[J].中国环境监测,2003,19(4):17-19.

[10] 薛文博,易爱华,张增强.基于韦伯—费希纳定律的一种新型环境质量评价法[J].中国环境监测,2006,22(6):57-58.

[11] 于露,李凡修.韦伯—费希纳定律在区域生态环境质量评价中的应用[J].油气田环境保护,2011,21(3):8-10.32.