基于PIPs样本优化的机车车辆轴温实时预测方法

杨则云



基于PIPs样本优化的机车车辆轴温实时预测方法

杨则云

（中车青岛四方机车车辆股份有限公司，山东 青岛 266111）

建立了一种基于最小二乘曲线拟合的轴温预测模型，并采用PIPs对样本进行优化改进，提高了预测精度。首先基于PIPs对建模样本点进行优化选择，选取历史温度数据中能表征温度变化趋势的重要点作为建模样本点，再利用最小二乘曲线拟合法建立实时温度预测模型对机车车辆轴承温度进行实时预测。以某型机车车辆履历轴承温度数据为例，采用本文模型对任意时刻温度的后5分钟温度进行预测，将预测结果与实际监测结果进行连续对比，验证了所建立的轴温预测模型及其改进模型的有效性：基于最小二乘曲线拟合预测模型的综合平均相对误差为3.47%，综合最大相对误差为20.27%，而进行PIPs改进后的综合平均相对误差为2.67%，同比降低了23.05%，综合最大相对误差为16.67%，同比降低了17.76%。

轴承温度；时间序列；曲线拟合；PIPs

热轴、燃轴是危及铁路运输安全的严重故障，表现为运行中轴承异常高热，轻则造成紧急停车导致经济损失，重则引发列车脱轨危及旅客生命安全。目前，由车轴异常发热引发的事故时有发生。温度是反映轴承热状态的最直接参量，温度突然升高或超过警戒值，是轴承异常运行和发生故障的重要信号。轴承磨损退化可能造成轴温升高，而正常工况下轴承转速、载荷、环境温度的变化亦可引起轴承温升[1]。轴承温升原因的不确定性[2-3]是基于温度信号进行故障诊断的难点。现有轴温监测系统预警规则根据绝对阈值进行报警，误报漏报现象频发且在温度达到阈值后再进行预警剩余处置时间不足。因此对车辆轴温进行实时预测，掌握轴温未来变化趋势，提前预警以便及时调整行车策略，具有重要意义。

为满足车辆轴承温度实时准确预测的要求，将轴承温度预测问题转化为基于轴承历史温度数据的时间序列预测问题。在轴承温度预测问题研究上，Han[4]等针对水电机组轴承的故障预测问题，采用自回归滑动平均模型（ARMA）对温升趋势进行预测，该模型只适用于线性系统的预测且不适用于长期预测，对机车车辆轴温这样的动态过程预测精度不足。文献[5-7]分别基于新陈代谢灰色模型、GA-BP融合算法、广义隐马尔可夫模型对轴承温升进行预测，但这些方法都只能进行短时预测，不能满足机车车辆轴温实时预测的要求。

曲线拟合可以直接通过最小二乘法估计模型参数来对函数近似，算法原理简单，不需要进行参数优化，并且实施方便、时间复杂度低，是一种典型的趋势预测方法。但在基于最小二乘曲线拟合的轴承温度预测中，由于历史温度数据呈现波动变化且存在噪点，建立的预测模型不能准确描述温度变化趋势，导致预测误差较大，针对这一问题本文提出结合PIPS[6]（Perceptually Important Points）样本优化的曲线拟合轴温预测方法。

1 PIPs算法和最小二乘曲线拟合预测算法

1.1 PIPs算法

时间序列由一系列的点构成，每个数据点的幅值对时间序列波形有不同程度的影响，序列中的少数点即可确定其波形，而序列中的剩余点可被忽略，PIPs由Chung，Fu等人[8]于2001年提出，用于寻找价格序列中的特征点，在数据挖掘中PIPs作为一种动态分割方法主要用于时间序列的表达，定义时间序列中的重要点，去除了序列中的波动点及噪声点的干扰，将时间序列非等间距地表出，准确表达了时间序列的变化趋势。

PIPs算法流程如图1所示，首先通过构造PIPs定义序列中的重要点，以序列起始点与最末点作为初始的两个PIPs，并计算序列中其余点与已定义PIPs距离，将距离最大的点定义为下一个PIPs，重复迭代这一过程，直至PIPs数量达到用户定义数量。用非等间距的PIPs对原序列进行重新表出。

图1 PIPs算法流程

1.2 基于最小二乘曲线拟合的预测算法

曲线拟合函数一般采用如下所示广义多项式线性模型：

式中：1，2，...，θ是模型的个参数；为模型自变量；（）为基函数。

对于给定组离散观测序列{x， y}，＝1，2，...，，模型可表示为：

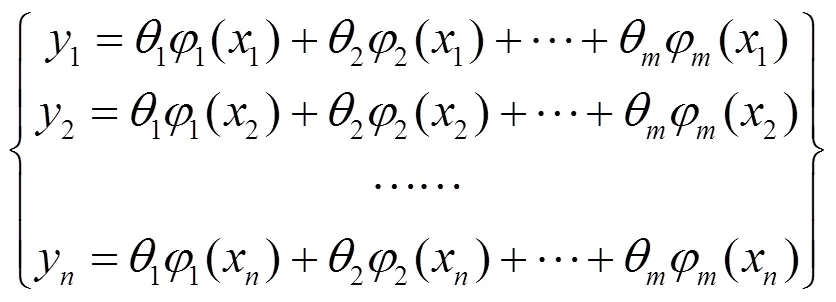
则模型可写成向量形式＝，将拟合值与实际值的离差平方和作为曲线拟合精度指标：

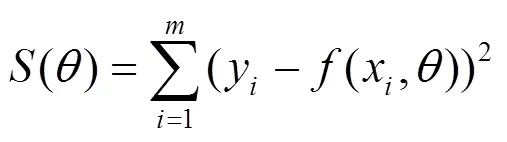
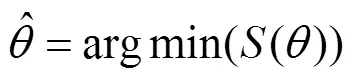
由曲线拟合原理可知，基函数的应用可以增加拟合模型的非线性能力，从而实现对曲线函数的逼近。不同的基函数对不同形状特点的曲线的逼近能力也不尽相同，所以基函数的选择对曲线拟合的精度有着直接影响。本文通过分析对比，选择幂函数作为曲线拟合的基函数。工程应用中常见的基函数有多项式模型、指数模型、幂函数模型。

多项式模型为：

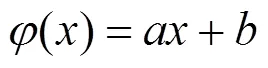
指数模型为：

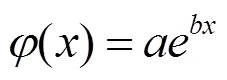
幂函数模型为：

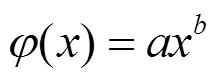
2 基于PIPs建模样本优化的轴温预测方法

轴温序列属于一种非平稳非线性的时间序列，容易受环境温度、运行线路、运行速度等因数的影响。如果利用所有前序轴温样本数据进行建模，其中所包含的噪声点会对模型预测结果造成较大的影响，本文采用的算法首先对历史轴温窗口内的轴温数据运用PIPs算法进行筛选后再构造样本空间，在降低时间序列维度和抑制噪声的同时，对重要的点也不会造成扭曲，保持了原始数据的准确性，实现了建模样本点的优化选择。再采用曲线拟合的方法构建预测模型，利用最小二乘法求解模型参数，输出预测曲线。最后综合考虑轴温变化趋势，根据预测曲线制定合理及时的预警策略。算法具体步骤如图2所示。

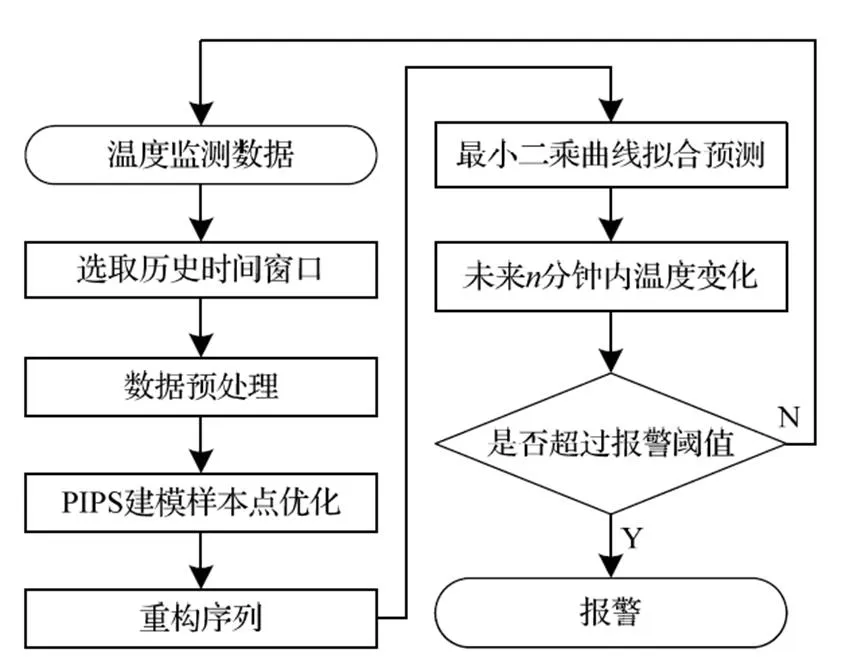
图2 基于PIPs建模样本优化的轴温预测预警流程

（1）通过插值对数据中的缺失点进行预处理。基于当前时刻的轴温序列，在其历史时间邻域内取一段长度为的历史轴温序列：

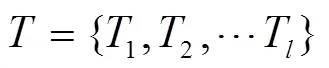
（2）定义重要程度相邻的两个点PIPS为χ＝{T，}和χ+T＝{T+T，+}，则下一个重要点为距离χ、χ+T最近的点，距离为：

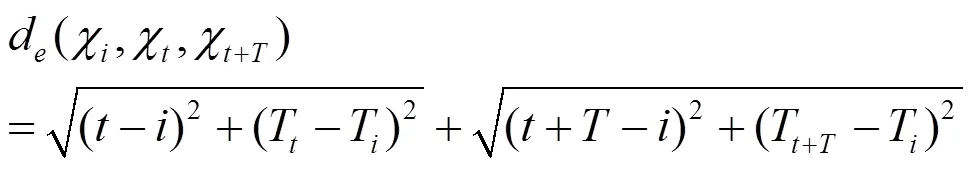
将温度序列的首尾两点初始化为最开始的两个PIPS，重复迭代计算即可得到所有的PIPS。

（3）按照重要程度对历史数据点进行筛选，重构为一段长度为的温度序列T，其对应的时间坐标序列为。

（4）构造曲线拟合模型，拟合基函数为幂函数（），拟合函数模型可用表示为：

（5）将重构后的实际监测数据{t，T}（＝1，2，...，）代入曲线拟合模型岢，可得：

将其向量化可得：

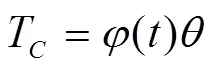
则轴温预测模型估计参数为：

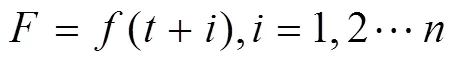
3 实例验证

3.1 实验条件

以某型机车车辆履历服役轴温监测数据为例，数据来源为某型机车车辆车载轴温监测系统测得的同列车上多个轴温测点温度，温度传感器为pt100，采样频率为1 Hz，监测轴温数据传输频率为每分钟一次。按每分钟一次的频率取1 min内测点温度最大值对实测温度值进行重采样，以齿轮箱相关轴承温度测点如表所示履历轴温数据进行验证，其位置分布如图3所示测点。选择相同的历史数据窗口预测后序5 min温度变化情况，分别用本文提出的基于PIPs建模样本点优化的曲线拟合法与曲线拟合法进行对比。

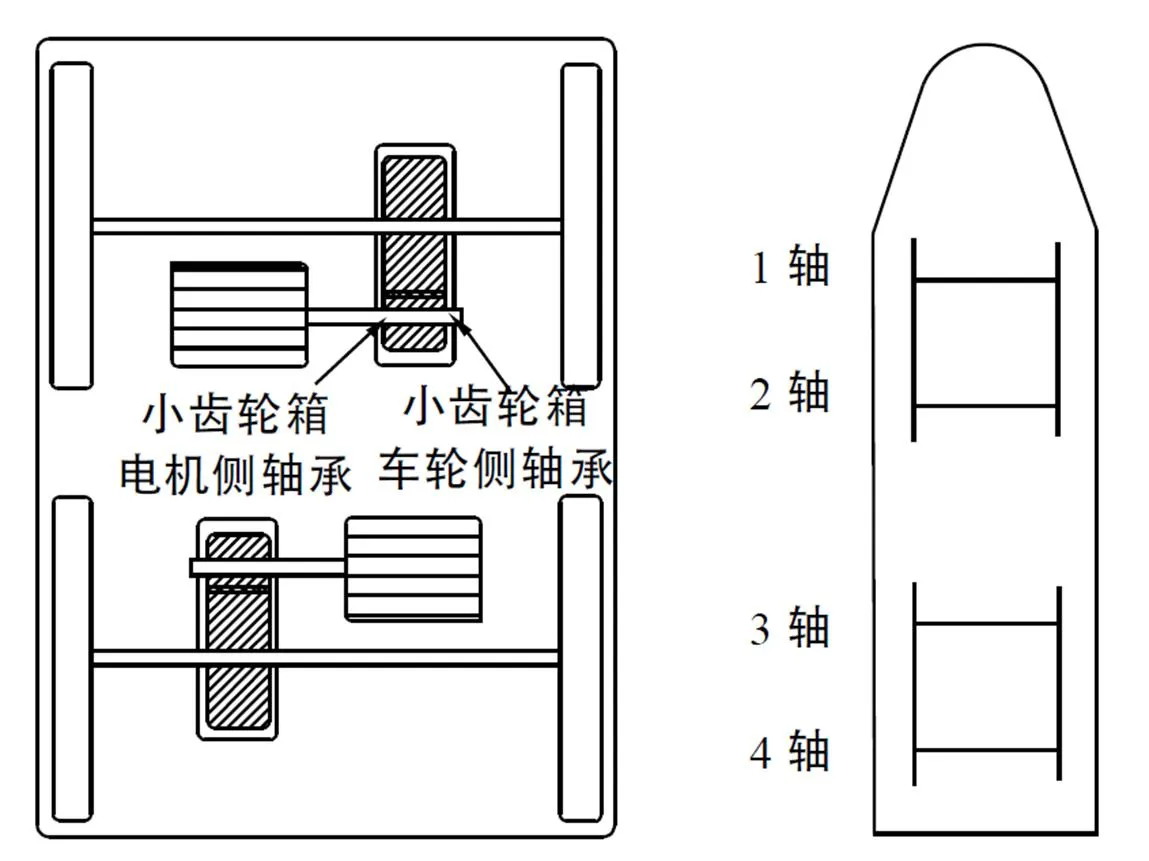
图3 机车车辆轴承位置分布

表1 轴温测点位置及通道编号

3.2 验证结果及分析

在当前主流的计算机配置条件下，每测点进行一次预测的运行时间约为30 ms，可以满足在线预测的实时性要求。基于本文模型和上述实验条件进行的5 min后续轴温的预测结果如表2所示。

表2和表3分别为改进前后两种方法的误差统计情况，表中各种误差的计算方法为（逐点对比预测值和实测值，时间间隔为1分钟）：

绝对误差＝|预测值－实测值|；

相对误差＝绝对误差/实测值；

平均绝对误差＝Σ（绝对误差）/总分钟数；

平均相对误差＝Σ（相对误差）/总分钟数；

最大绝对误差＝Max（相对绝差）；

最大相对误差＝Max（相对误差）。

对算法的评价采用综合平均相对误差和综合最大相对误差。其计算方法为：

综合平均相对误差＝Σ（各通道的平均相对误差）/通道数；

综合最大相对误差＝Max（各通道的最大相对误差）。

表2 基于最小二乘曲线拟合预测模型的预测误差

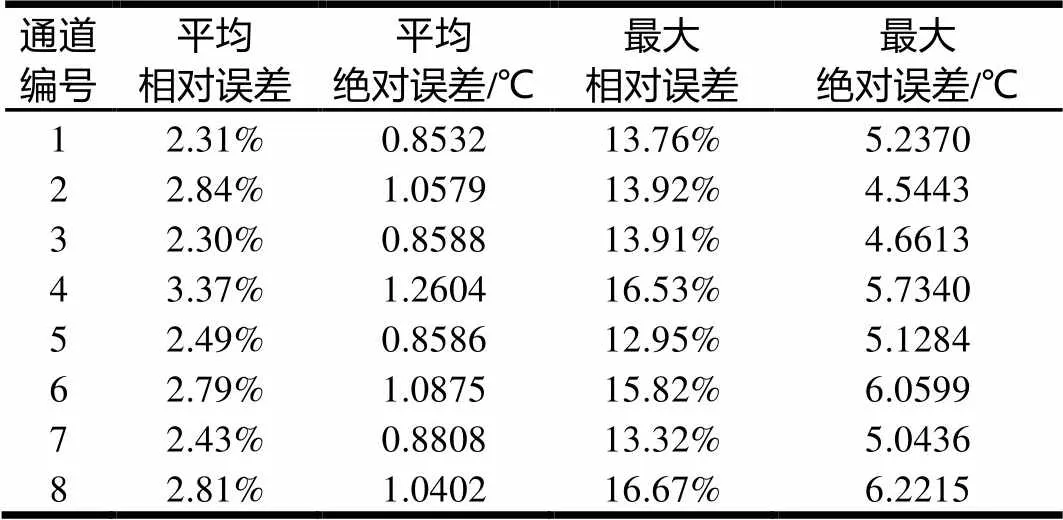
表3 基于PIPs对建模样本优化改进后的预测误差

从公式可以看出，综合平均相对误差可以反映出算法对于所以通道的适应性和预测准确度，而综合相对最大误差可以反映出预测值和实际值的偏离程度，因此选其作为评价指标。

从表2和表3中可以看出，基于最小二乘曲线拟合模型的预测综合平均相对误差为3.47%；综合最大相对误差为20.27%。进行PIPs样本优化后的预测模型的综合平均相对误差为2.67%，同比降低23.05%；综合最大相对误差为16.67%，同比降低17.76%。

表4为基于PIPs建模样本优化后的误差相比优化前的降低率，计算方法为：

预测误差降低率＝（改进前预测误差－改进后预测误差）/改进前预测误差。

通过表4可以发现，从各通道的平均相对误差降低率看，改进后的模型对于各通道的预测误差率都有15%以上幅度的降低，从最大相对误差降低率看，改进后的模型对于各通道的预测误差率降低率也比较显著，最高达到36.11%。

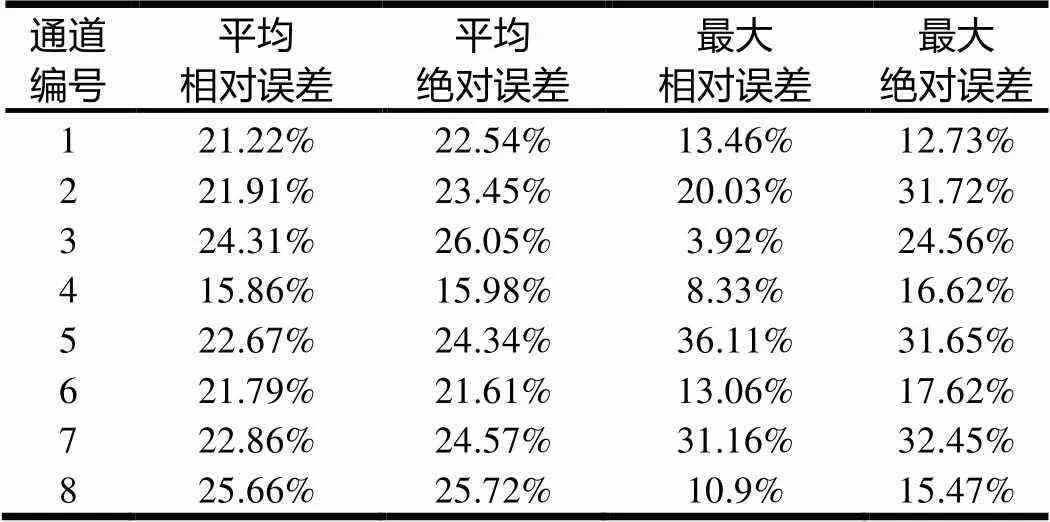
表4 优化后比优化前预测误差降低率

以综合改进效果比较明显的通道5为例，其实测值、基于最小二乘曲线拟合模型的预测值、PIPs样本优化后的预测值如图4所示。

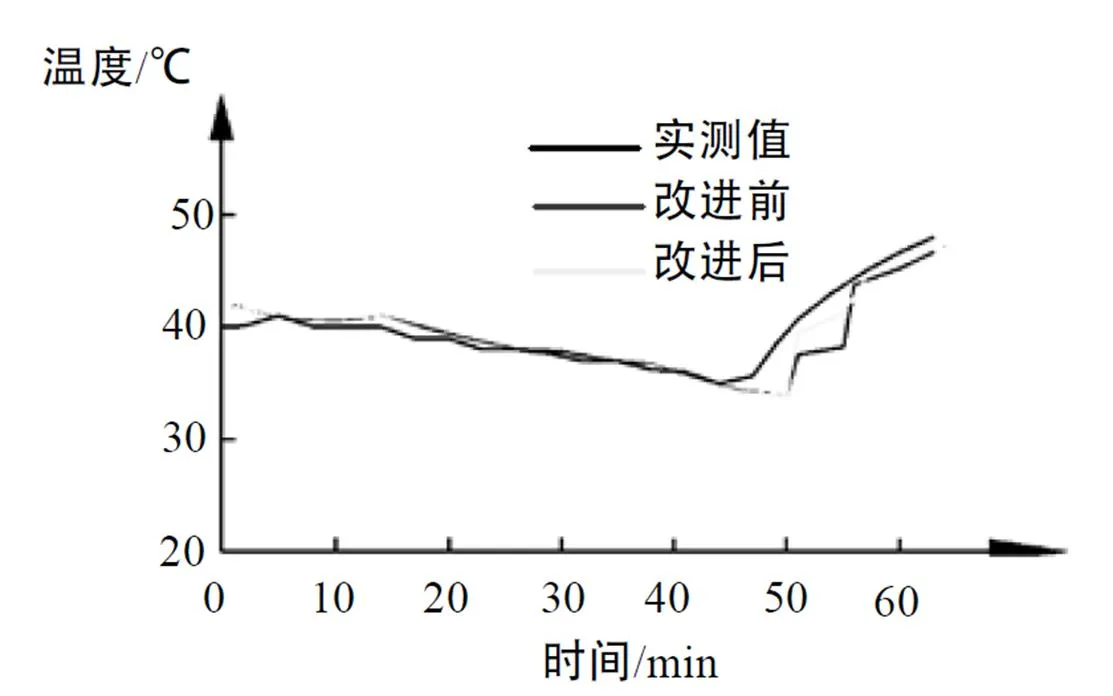
图4 改进前后1轴小齿轮箱车轮（5通道）侧轴承预测曲线

4 小结

针对基于最小二乘曲线拟合的机车车辆轴承温度在途预测中存在的预测误差较大问题，本文结合PIPs方法进行建模样本优化选择，选取序列中重要点对历史轴承温度序列进行重新表出，去除序列波动，噪声点的影响，准确描述温度变化趋势，再基于优化后的样本点运用最小二乘拟合进行温度预测，并基于某型机车车辆履历数据验证了方法的有效性，结果表明基于PIPs样本优化的曲线拟合预测方法能够满足机车车辆轴承在途预测准确性与实时性要求，对保障车辆安全运行具有一定意义。

[1]Zhou W，Habetler T G，Harley R G. Bearing condition monitoring methods for electric machines: A general review[C]//Diagnostics for Electric Machines，Power Electronics and Drives，，2007. SDEMPED 2007. IEEE International Symposium on. IEEE，2007：3-6.

[2]王跃飞，孙启国，牛鹏. 基于Fluent的轴承腔温度场仿真分析[J]. 机械，2014，41（3）：24-27.

[3]朱亮亮，林素敏，吕秋硕，等. 滚动轴承寿命计算方法的优化[J]. 机械，2015，42（2）：20-24.

[4]Fengqin Han，ZhonghuaGui，Kubota Takashi.Singular Spectrum Analysis-based prediction of bearing temperature trend and its application[J]. Journal of South China University of Technology（Natural Science Edition），2005，33（9）：51-54.

[5]曹寅冬. 基于新陈代谢GM（1，1）模型的客车轴温预测算法[J].铁道机车车辆，2011，31（1）：49-51.

[6]莫丽，王军，王俊，王禄友. 基于GA-BP算法的旋转控制头轴承温度预测[J]. 西南石油大学学报（自然科学版），2016，38（1）：164-169.

[7]王小岑，胡友名，吴波，谢锋云，金超. 广义隐马尔科夫模型在轴承温升预测中的应用[J]. 自动控制与检测，2013（6）：54-57.

[8]Chung F L，Fu T C，Luk R，et al. Flexible time series pattern matching based on perceptually important points[C]. Proceedings of the international joint conference artificial intelligence workshop Seattle：August 2001：1–7.

A Real-Time Temperature Prediction Method Based on PIPs Sample Optimization for Train Bearings

YANG Zeyun

( CRRC QINGDAO SIFANG CO., LTD., Qingdao 266111, China )

In this paper, a bearing temperature prediction model based on the least square curve fitting is established, and the sample is optimized by using the perceptually important points to improve the prediction accuracy. First, the modeling sample points were selected from historical temperature data which can represent the important points of the temperature change trend based on the PIPs, then least squares curve fitting was used to establish a real-time temperature prediction model of train bearing temperature real-time prediction. According to a train bearing temperature data, use this model to predict temperature in the next five minutes. Compared with the actual measurement results, and it shows that the proposed temperature prediction model is valid: the total average error of the prediction model based on the least squares curve fitting is 3.47%, the total maximum relative error is 20.27%. After the improvement of PIPs, the total average prediction error is 2.67%, reduces 23.05% compared with before. The total maximum relative error is 16.67%, reduces 17.76% compared with before.

bearing temperature；time series；curve fitting；PIPs

TK730.3+22；TF068.21

A

1006－0316 (2018) 04－0001－06

10.3969/j.issn.1006-0316.2018.04.001

2017－11－20

国家高新技术研究发展计划（863）计划（2015AA043701）

杨则云（1980－），天津人，硕士，高级工程师，主要研究方向为机车车辆安全技术及管理。