Delta机器人传送带与视觉的标定方法
2018-05-16,
,
(西安工程大学 控制工程,西安 710048)
引 言
跟踪抓取的精度是机器人实现抓取的前提,所以前期对于机器人的标定、相机的标定、传送带的标定有着更高的要求。曾有人提出一种测量系统的精度,有一种双经纬度测量系统球杆仪,这种可以精确测量末端点与工作空间之间的距离,但是这种测量有特殊的设备与专业的技术,时间长、成本高。本文通过摄像机的标定求出内外参数,得到机器人的坐标系与摄像机的坐标系关系,在计算出传送带原点坐标系与机器人之间转换矩阵与比例因子、传送带与机器人之间的相对位姿,从而使得机器人、传动带、摄像机构成一个闭环,能更准确地抓取物体。此方法避免了传送带与摄像机安装角度偏差,并且成本低,易于操作、精度也相对比较高。这对标定方法具有使用价值。
1 视觉标定
摄像机的几何模型如图1所示,其中平面Z为摄像机投影平面,坐标系X,Y,Z为图像坐标系,Xw,Yw,Zw为世界坐标系,[U ,V]为图像坐标系,[X,Y]为像点坐标系。P是世界坐标系中的点,它在摄像机坐标系中的坐标为(Xc,YC,ZC),在世界坐标系中的坐标为(Xw,Yw,0),P′是对应于点P在摄像机投影平面上的点,它在像点坐标系中的坐标为(x,y),在图像坐标系中的坐标为(u ,v)。
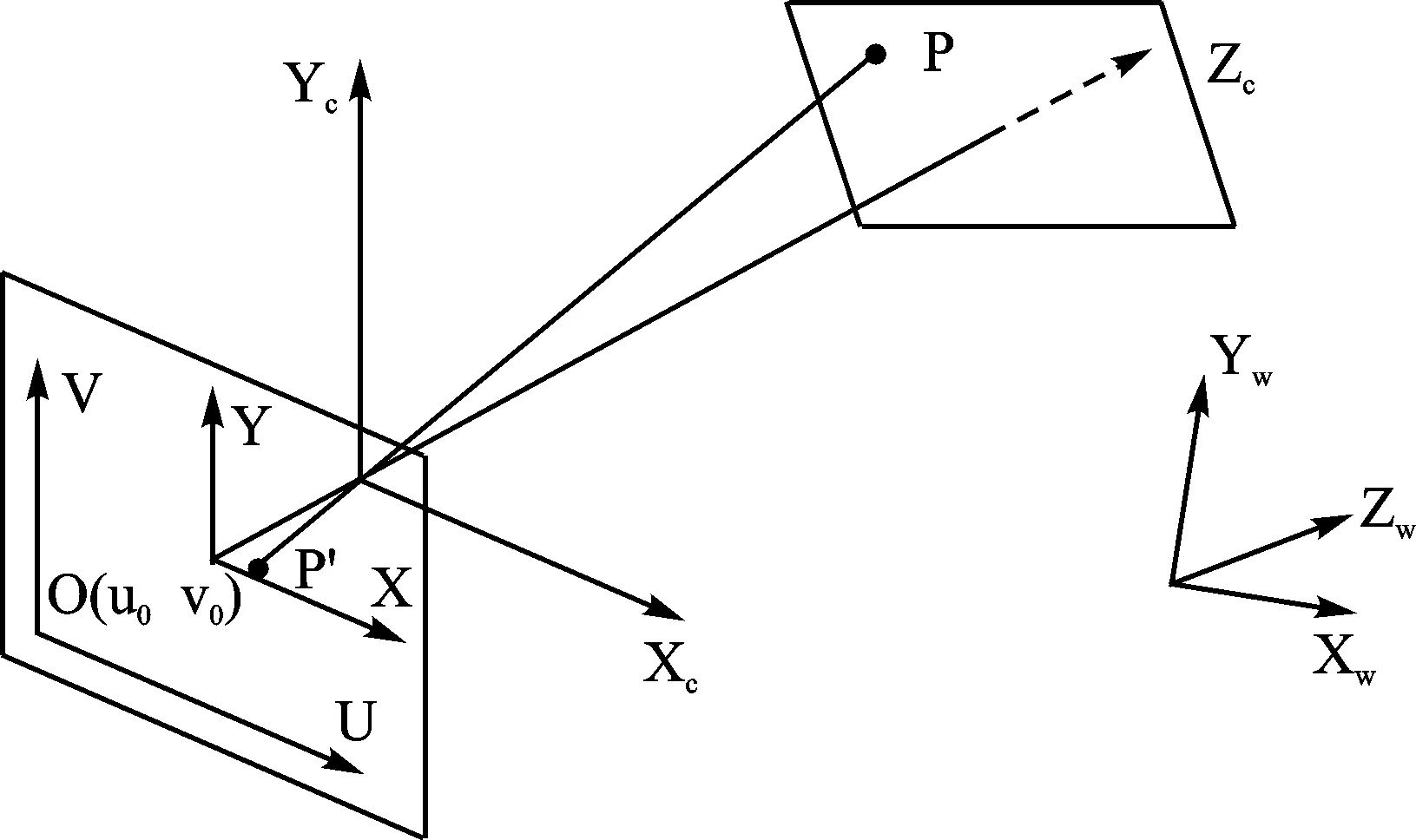
图1 摄像机几何模型
由于点P与点P′是对应点,根据小孔成像原理可以得到:
(1)
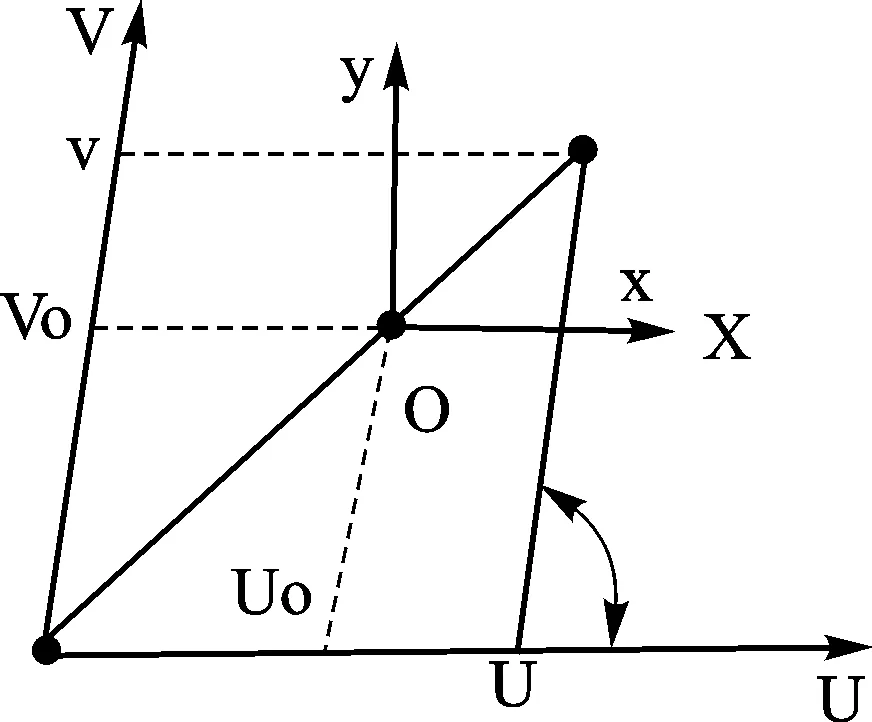
图2 摄像机内部模型图
其中f表示摄像机的焦距。
摄像机内部模型图如图2所示。
(2)
由式(1)和式(2),可以知道:
(3)
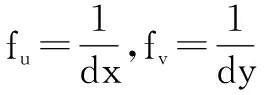
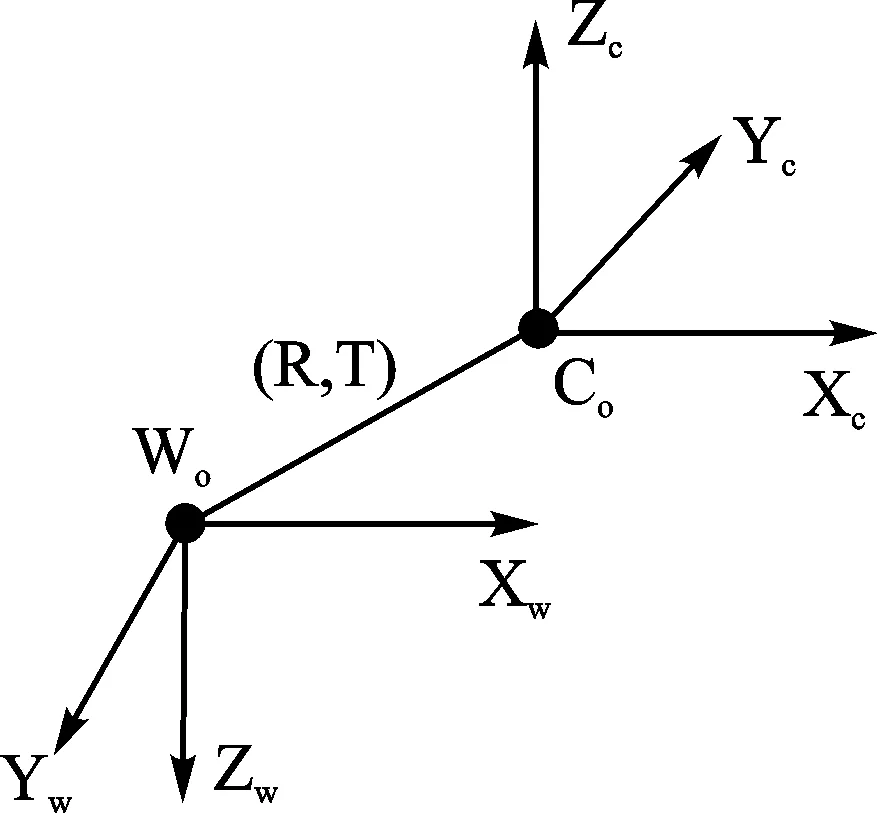
图3 所示世界坐标系与摄像机坐标系
根据图3所示,世界坐标系与摄像机坐标系是通过转化矩阵与旋转矩阵进行相互转化,由上图知,世界坐标系是通过绕Xw旋转θ角度。根据矩阵的基本旋转可知:
T=[t1t2t3]T
2 传送带的标定
编码器的运用非常广泛,一般可分为两种类型:绝对式和增量式。本文中传送带用到的是绝对式编码器,绝对式编码器就是对应一圈,每个基准的角度发出唯一对应的二进制数值,通过外部的计圈器件可以进行多个位置的记录和测量,L是传送带移动的位移,T是运动的时间,通过式(5)
(5)
计算出传送带的运动速度V,这是求解转换矩阵与比例因子必不可少的环节。
2.1 转化矩阵与比例因子求解
ΔLr=[(X1-X2)2+(Y1-Y2)2+(Z1-Z2)2]1/2
(6)
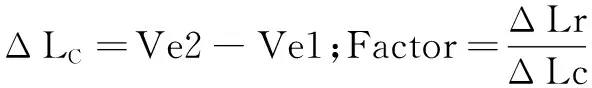
(7)
ΔLr是图4所示C与C′的距离;ΔLC是在两点时编码器对应的值的差;Factor是比例因子。转换矩阵是确定传送带相对于机器人原点的坐标系变化的矩阵。
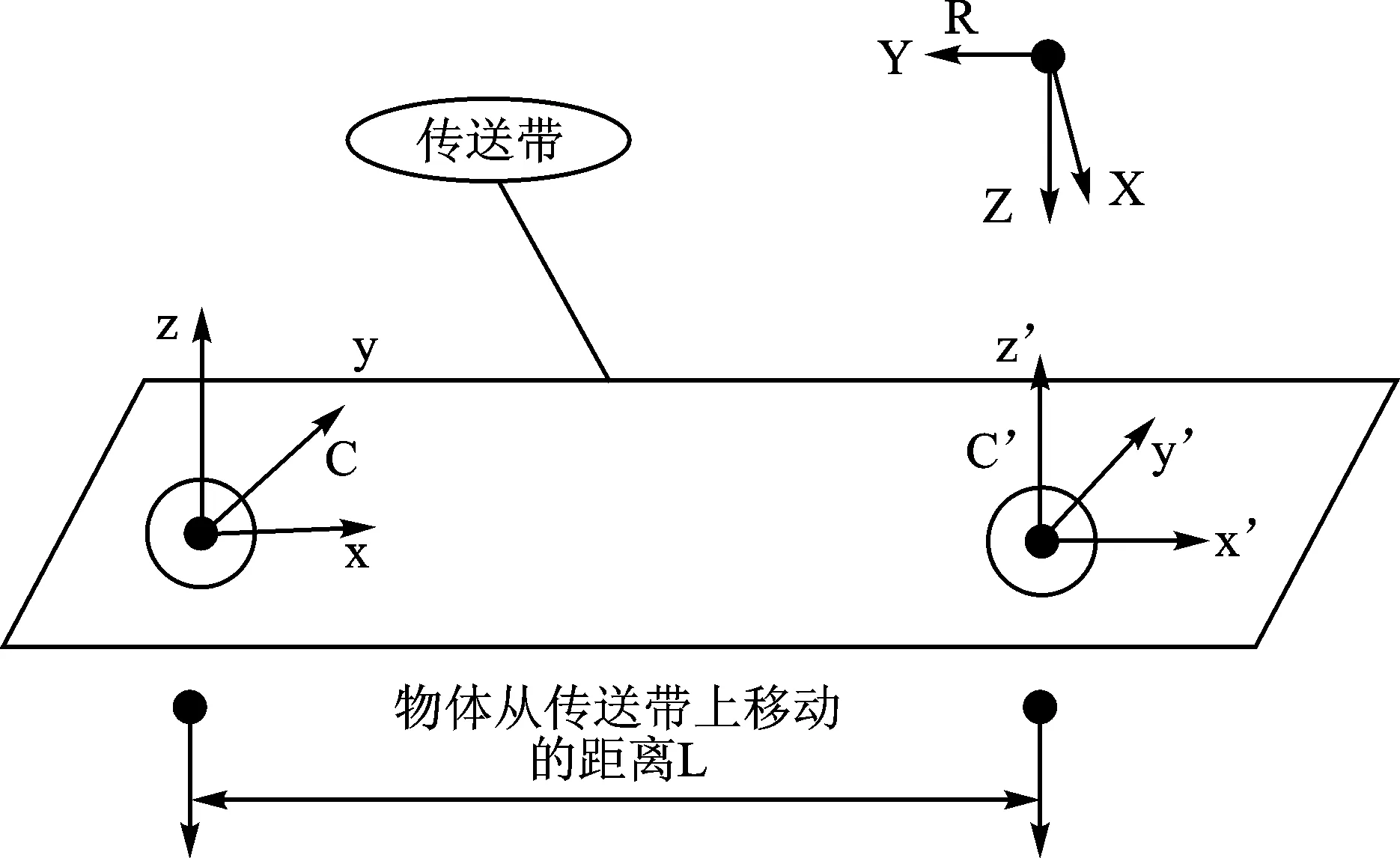
图4 传送带与机器人的示意图
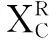
2.2 传送带标定的方法
① 在传送带上确定一点P1,通过示教盒移动机器人,将末端触头移到点P1的正上方,并且记录传送带的编码器的值为 Ve1,机器人此时末端的位姿为RP1(X1,Y1,Z1)。
② 移动传送带并且保证机器人可以触碰到P2点的条件下,让这段移动的距离越大越好,再次移动机器人使末端触到点P,记录编码器的值Ve2,机器人的末端位姿RP2(X2,Y2,Z2)通过上述步骤以后,可以得到编码因子。
③ 得到编码因子后,当移动传送带时,记录新的P1与P2点两个编码值后,通过比例因子得到机器人移动的距离。然后让机器人沿着传送带垂直的方向移动一段距离,记录机器人末端的位姿RP3(X3,Y3,Z3)。
④ 根据图所5所示P1、P2、P3这三个点都是在机器人坐标系下的点。设C′点是传送带相对于机器人的坐标系原点。计算出坐标系的原点就可以求出机器人与传送带之间的坐标系关系。
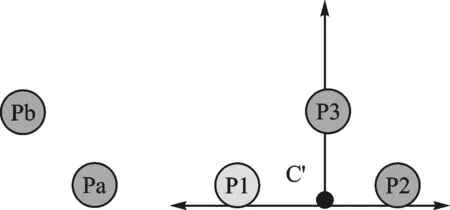
图5 传送带标定的示意图
⑤ 根据三角形的计算公式

3 基于传送带视觉的标定
从上述得到机器人与传送带之间的关系,如果再求出传送带与视觉之间的关系,就可以得到机器人与物体的关系。
3.1 标定的方法
视觉系统固定在传送带正上方,当物体进入视觉范围,通过对物体的图像处理获取物体的中心点,以此中心点建立坐标系,并且以传送带运动方向为x轴正方向,y轴方向与x轴方向垂直,z轴与传送带平面垂直。
① 在传送带上放一个物体而且要保证此物体在视觉范围内,通过视觉记录一个值H1(x1 y1 z1)。
② 移动传送带一段距离,但是不能超出视觉范围,再记录另一点的值H2(x2 y2 z2)。
通过上述H1、H2两点以及公式:
(9)
可以计算出摄像头安装的角度与传送带的角度之间的夹角θ。
这样做的原因是避免了传送带与摄像头之间因角度的偏差引起不必要的误差。由上述知道传送带的原点坐标系,通过矩阵的转换求出传送带坐标系与机器人坐标系的关系,再通过机器人与摄像机的坐标系关系转换,最终得到了传送带与摄像机的坐标系之间的关系。机器人就可以准确地知道物体的位置。
3.2 试验与数据
传统的标定方法,测量摄像机内外参数是不太精确的,相对精度比较差。传统的方法没有考虑到摄像机的安装角度对于传送带的偏差。本文既考虑了摄像机的安装角度的偏差,也考虑到了传送带的角度。表1是在机器人
坐标系下测量的4组数据。
通过实验得出的数据,本文的标定方法比传统标定方法的精度更高,相对而言更实用。

表1 实验数据
结 语

参考文献
[1] 吴宗森.基于机器视觉的Delta并联机械手臂控制技术研究[D].成都:电子科技大学,2016.
[2] 李小辉.Delta并联机器人视觉分拣与跟踪系统设计与研究[D].广州:华南理工大学,2016.
[3] 殷国亮.基于机器视觉的DELTA机器人实时控制系统的研究与开发[D].无锡:江南大学,2015.
[4] 邓明星,刘冠峰,张国英.基于Delta并联机器人的传送带动态跟踪[J].机械工程与自动化,2015(1):153-154,156.
[5] 邓明星.并联Delta机器人的传送带动态抓取系统设计[D].广州:广东工业大学,2014.
[6] 曾奇.Delta并联机器人运动学标定[D].广州:广东工业大学,2014.
[7] 商大伟.高速Delta并联机器人系统的集成与测试[D].青岛:中国海洋大学,2014.
[8] 张文昌,梅江平,刘艺,等.基于激光跟踪仪的Delta并联机构运动学误差标定[J].天津大学学报,2013(3):257-262.
[9] 张文昌.Delta高速并联机器人视觉控制技术及视觉标定技术研究[D].天津:天津大学,2012.
[10] 唐国宝,黄田.Delta并联机构精度标定方法研究[J].机械工程学报,2003(8):55-60.
高盼、柯丽红(硕士),主要研究方向为机器人技术。
