神经元PID在风力摆控制系统中的应用

徐涢基，方 平，李 娜，谭尾琴，毛启宁

(1.华东交通大学理工学院，江西 南昌 330100；2.江西警察学院安全管理系，江西 南昌 330103)

0 引言

风力摆控制系统[1-2]是控制系统中典型的控制模型。该系统以风机作为动力源，能够很好地验证PID算法的效果。

目前，在自动控制原理的学习与设计过程中，由于控制模型昂贵、复杂，难以将控制理论很好地与实践相结合，学习效果较差，设计难度较大。因此，设计一款性价比高、调试方便的PID控制系统，对提升自动控制原理的学习效果、降低自动控制系统设计难度意义重大。

本文在充分研究了PID控制算法基础上，设计了一款风力摆控制系统模型[3]。为验证PID控制[4]的效果，设计任务如下：让空心杯电机驱动摆在竖直面来回摆动，使摆下方激光笔的光照到地面上。在地面画出一条长度不小于40 cm的直线，要求画出的线长度为(40±2.5) cm，偏离原定地面轨迹不超过±2.5 cm。实践测试验证了设计的可行性。

1 风力摆模型及关键器件选择

风力摆模型如图1所示。

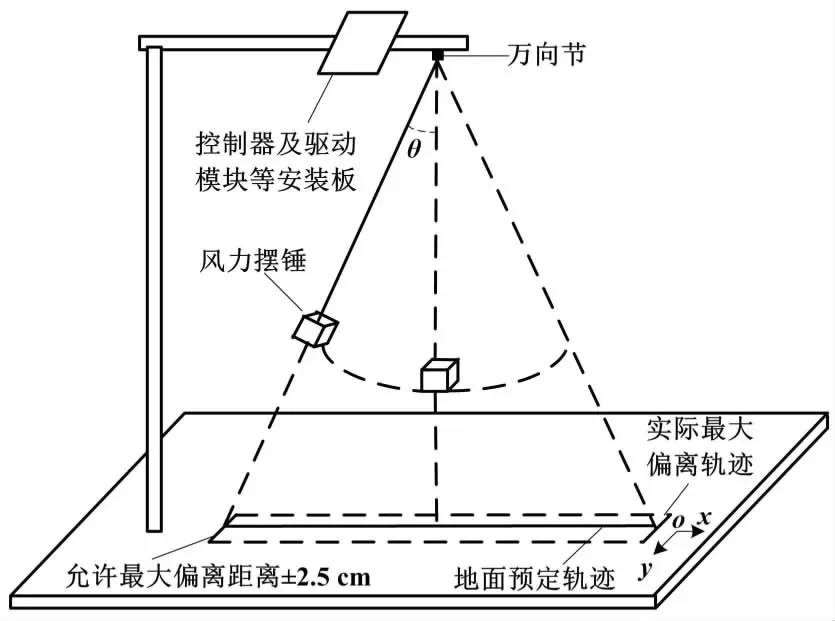
图1 风力摆模型Fig.1 Model of wind pendulum

风力摆摆杆选用质硬且较轻的玻纤管,上端通过万向节固定在硬质悬臂梁上,玻纤管的下端穿过(10×10) cm的正方形丙烯腈-丁=烯-苯乙烯(acrylonitrile-butdiene-styrene,ABS)板正中心，并用热熔胶将ABS板与玻纤管垂直固定。玻纤管最低端与激光发射头固定，且在风力摆处于自然下垂时，使激光如图中间虚线照射到地面平板上。六轴陀螺仪MPU6050水平安装在ABS板上，且在陀螺仪x和y轴方向的ABS板两边中间位置各安装两个空心杯电机。四个电机的驱动模块安装在悬臂梁上端的安装板上。

为了实现上述任务要求的功能，采用如下方案。

①电机。

风力摆控制系统在竖直方向来回摆动。820空心杯电机配备75 MM A+B螺旋桨，工作电压3～5 V，电流0.15 A。在工作电压为3 V时，转速为35 000～37 000 r/min，在工作电压为5 V时，转速为50 000 r/min。

②电机驱动电路。

根据风力摆需要完成任务的要求，选用TB6612FNG电机驱动模块。该款驱动模块是一种双驱动，可以同时驱动两个电机。该模块的AIN1、AIN2、BIN1、BIN2用来控制正反转，可以通过其控制电机工作在“停止、正转、反转”三种工作模式。当AIN1与AIN2电平为00或11时，电机工作在停转状态；当AIN1与AIN2为电平为01或10时，电机工作在正转或反转状态。驱动模块上PWMA为第一路电机PWM控制端口，用于电机调速使用，BIN1、BIN2与AIN1、AIN2类似。

③陀螺仪MPU6050。

为了能够实现任务，需要测定当前风力摆来回摆动时偏离竖直方向的摆角，以及测定当前摆动轨迹与预定轨迹偏离幅度。本控制系统选用的角度传感器为六轴MPU6050。该传感器含有三轴陀螺仪[4-6]和三轴加速度，工作电压范围为3～5 V，采样通信速率高达400 kHz的IIC通信协议，内置16位A/D转换器，可以输出16位数字信号。其角速度测定范围(°/s)：±250、±500、±1 000、±2 000。加速度范围：±2g、±4g、±8g、±16g。该传感器应用非常广泛，如“运动感测游戏”，“现实增强”和“电子稳像”以及“光学稳像”，“零触控手势用户接口”，“姿势快捷方式”和“认证”等领域。

④微控制单元。

根据需要处理数据的情况，选用了一块IAPSTC15W58S4作为微控制单元。该款微控制单元拥有8通道10位ADC，速度可达30 万次/s，6路脉宽调制信号(pulse width modulation,PWM)、6路DAC、6通道捕获/比较单元，不需外部晶振，内部时钟从5～35 MHz可选。

2 神经元PID控制算法及算法实现

2.1 神经元PID控制算法

PID控制在控制系统中应用较为广泛，目前90%以上的控制系统仍然以PID控制或其改进PID控制作为系统的主要控制算法，其应用非常广泛。

PID控制结构示意图如图2[6-7]所示。

图2 PID控制结构示意图Fig.2 Schematic diagram of PID control structure

PID控制相应的控制算式[6]为：

(1)

式中：θ为控制端输出；θ0为偏差为零时θ的初值；e(t)为神经元PID控制器输入函数，即给定量与输出反馈量的偏差；KP为比例增益；TI为积分时间常数；TD为微分时间常数。

将式(1)展开，函数可分成比例控制、积分控制和微分控制三部分。核心控制器计算公式一般为离散分量，将差分方程改写为：

(2)

(3)

式中：T为采样周期；k为采样序号；e(k-1)和e(k)分别为第(k-1)次和第k次控制净输入端的偏差。

综合以上各式，可得出差分方程为：

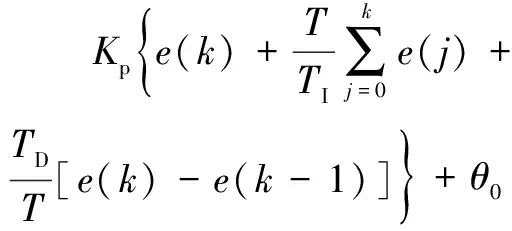
(4)

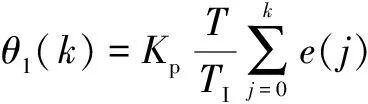
2.2 系统软件及算法设计

系统主程序流程如图3所示。系统初始化主要需要对GPIO、Uart、MPU6050、M1TypeDef、M2TypeDef、PID_M1、PID_M2和关于定时器T2的相关寄存器进行初始化，不断采集传感器MPU6050的x、y、z方向的角度和角加速度数据，最后控制电机,执行任务。

图3 系统主程序流程图Fig.3 Flowchart of system main program

iError=M1PID.SetPoint-NextPoint

(5)

M1PID.SumError+=iError

(6)

dError=iError-M1PID.LastError

(7)

M1.PWM=M1PID.Proportion*iError+M1PID.Integral*M1PID.SumError+

M1PID.Derivative*dError

(8)

式中：iError为X方向角度偏差值；M1PID.SetPoint为X方向角度设定值；NextPoint为X方向下一次偏差角度值；M1PID.SumError为X方向角度偏差积分值；dError为X方向角度偏差微分值；M1PID.LastError为X方向当前角度偏差值；M1PID.Proportion为X方向比例参数P值；M1PID.Integral为X方向积分参数I值；M1PID.Derivative为X方向微分参数D值。

Y方向控制算法与式(5)～式(8)类似。

风力摆控制系统PID算法流程如图4所示。

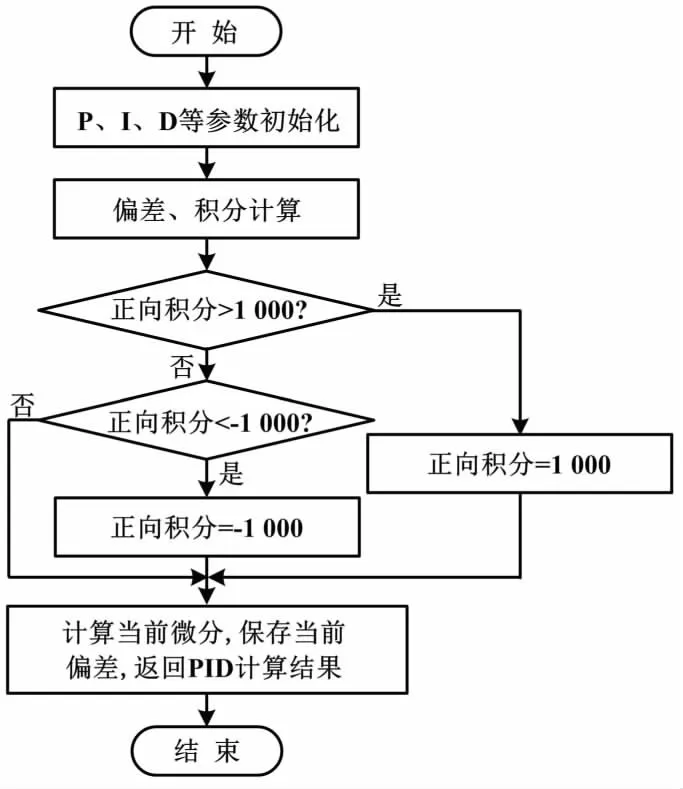
图4 PID算法流程图Fig.4 Flowchart of PID algorithm

任务执行流程如图5所示。

图5 任务执行流程图Fig.5 Flowchart of task execution

首先对系统参数进行初始化，主要有风力摆周期、运算时间间隔、x和y方向的预定摆角等。然后再设置运算间隔为6 ms，并根据如下公式：

(9)

Omega=2×3.141 59×Normalization

(10)

(11)

set_y=A×sin(Omega)×0.58

(12)

式中：Normalization为风力摆周期归一化值；MoveTimeCnt为运算时间间隔；priod为风力摆周期；Omega为2π归一化值；A为最大摆角；l为水平摆线长度L的二分之一；H为摆杆万向节离地高度；常数57.295 8为换算系数，1弧度=57.295 8°；set_y为当前摆角；0.58为实际计算摆角与测定摆角之间修正系数。修正的主要原因为MPU6050陀螺仪，在跟随风力摆摆动过程中会出现失重现象，具体修正值需要根据实际数据计算得出。

最后，设置x和y方向PID跟踪目标值，再根据软件“SerialChart”图形显示区的图形形状，对P、I、D参数进行整定，最终控制电机工作，达到预定目标。

3 控制效果测试分析

通过两种途径对控制效果进行分析。第一种途径可以借助串口数据绘图软件SerialChart。该软件将从串口接收到的数据重新绘制成曲线图。将曲线图与预定曲线进行对比，分析是否达到设计要求，从而对PID参数进行整定[8-10]。第二种途径是观测实际运行轨迹与预定轨迹的偏离程度是否符合设计要求。本设计采用第一种方法。

3.1 串口数据及图形

串口数据接收与绘图软件“SerialChart”的关键在于设置好配置文件。需要设置的主要参数有：串口号、波特率以及要显示数据的最大值、最小值和曲线颜色等。x、y方向数据曲线如图6所示。由图6可以看出，峰值较接近，说明实际摆动幅度与理想值较吻合。

图6 x、y方向数据曲线Fig.6 x、y-direction data curves

3.2 偏差数据分析

风力摆摆锤实际轨迹与设定轨迹偏差数据对比如表1所示。根据摆幅平均偏差=tan(摆角偏差平均值)×90.5，求出x与y轴摆幅平均偏差值分别为-0.09 cm和0.78 cm。该摆幅偏差值满足偏差小于±2.5 cm的要求。

表1 摆幅偏差数据对比Tab.1 Comparison of swing deviation data cm

4 结束语

PID控制算法是一种非常经典而广泛应用的控制算法。本设计将其应用于风力摆控制系统当中，通过设置风力摆需要完成的动作，来测试PID控制算法在该控制系统中的效果。在设计与测试该风力摆过程中发现，该系统的关键在于选择好硬件型号并将PID算法应用于风力摆控制系统中，并熟练地使用SerialChart软件对P、I、D参数进行整定。实际测试情况证明，该风力摆控制系统x、y轴摆幅偏差均较小，摆幅最大平均偏差只有摆幅40 cm的0.225%。该方案完全可以完成预定的要求。

参考文献:

[1] 宫玉芳，赵霞，杨志飞.基于K60的风力摆控制系统设计[J].自动化与仪器仪表，2016，20(10)：67-69.

[2] 苏宁远，张晨亮.基于MK60FN1MOVLQ15的风力摆控制系统设计[J].仪表技术,2016(8)：23-25.

[3] 姜香菊,刘二林.旋转倒立摆的起摆与稳摆研究与实现[J].自动化仪表，2016，37(9)：6-9.

[4] 王威，杨平.智能PID控制方法的研究现状及应用展望[J].自动化仪表，2008，29(10)：1-4.

[5] 赵海涛，郭少娟.基于神经元PID的SCR脱硝控制系统研究[J].自动化仪表，2017，38(5)：20-23.

[6] 王晓雷，赵向阳，刘玉翠，等.微陀螺仪检测控制系统设计与实现[J].自动化仪表，2016，37(7)：50-53.

[7] 陈存，路林吉.基于模糊PID算法的服装送带机控制系统[J].自动化仪表，2017，38(4)：37-40.

[8] 陆伟男，蔡启仲，李刚,等.基于四轴飞行器的双闭环PID控制[J].科学技术与工程，2014，14(33)：127-131.

[9] 张静，张华，刘恒,等.微型四旋翼无人机模糊PID控制[J].兵工自动化，2014，33(6)：58-62.

[10]曹刚.PID控制器参数整定方法及其应用研究[D].杭州：浙江大学，2004.