基于近邻保持嵌入的卫星姿态控制系统微小故障检测*
2018-05-15陆宁云
刘 敏,陆宁云,肇 刚,姜 斌
0 引 言
卫星在轨运行期间将大量的遥测数据传送到地面.当卫星处于异常状态时,遥测数据的特性也会发生相应的变化.例如,当系统部件受到外界干扰或逐渐老化时,卫星姿态控制系统(ACS)中的组件、执行器和传感器均可能发生故障[1],这些故障可能导致能耗增大、设备操作失灵甚至姿态失控等严重后果[2].因此,开展基于高维遥测数据的卫星姿态控制系统的故障检测研究十分必要.许多学者在这方面进行了研究,文献[3-5]通过对20世纪70年代以来国内外卫星的典型在轨故障进行分析,总结出姿轨控分系统所占故障比例高且主要集中于陀螺、动量轮和推力器等部件,其中的渐变微小故障在故障初期难以检测,随着时间的推移可能影响卫星的正常姿态从而导致卫星失效.这种处于早期阶段,幅值小且变化缓慢,故障特征不明显的微小故障若不能被检测并得到及时处理,将造成严重的后果[6].
现有的微小故障诊断方法往往依赖于传统的故障诊断方法,通常可被划分为基于专家系统的方法、基于解析模型的方法和基于数据驱动的方法[7].其中,基于数据驱动的微小故障诊断方法不依赖系统的先验知识,以监测数据为研究对象,表征系统运行的正常模式和故障模式[8],适用于卫星等复杂航天器设备的故障检测与诊断.文献[8]将数据驱动的微小故障诊断方法进一步细分为基于统计分析的方法、基于信号处理的方法和基于人工智能的方法,其中,基于多变量的统计分析方法能较好刻画并利用变量之间的相关性,适用于高维系统的故障检测与诊断.ZHOU[9]采用基于维纳滤波的噪声消除算法来分离定子电流中的轴承故障相关部件,从而检测到微小的轴承故障.SARAVANAN等[10]以齿轮箱中的故障产生的振动信号为研究对象利用离散小波变换实现对微小故障的特征提取.文献[11-15]通过将统计知识与主成分分析方法结合,利用新的检测指标实现对微小传感器故障的检测.但是这些方法仅关注于全局的欧式结构,在假设数据为线性结构的基础上利用优化准则寻求最佳的线性模型.
实际上卫星姿态控制系统具有高度非线性特性,其各个参量遥测数据之间往往具有非线性关系;另一方面高维的数据集具有低维内在几何嵌入结构,通过一般的线性方法无法寻找到数据完整的特征信息[16].随着对高维非线性结构的深入研究,学者们提出了流形学习的概念,文献[17-18]研究了基于局部线性嵌入(LLE)的非线性故障检测方法.本文作者在前人研究的基础上,将EWMA引入LLE算法,鉴于EWMA方法可以实现历史故障信息累积,从而实现了对卫星微小故障的检测[19-21].然而,EWMA-LLE方法没有考虑到样本外点问题(out-of-sample),即缺乏明显的投影矩阵,不能直接映射新加入的测试点.当新样本点加入时,该算法容易引起故障漏检与误报.
为了克服上述问题,本文将局部线性嵌入算法的线性扩展——近邻保持嵌入算法(NPE)作为研究方法.但是,传统NPE是通过欧氏距离选取近邻,对近邻参数十分敏感,参数往往由反复试验确定,运行效率低.不仅如此,NPE方法通常对初期故障不敏感,对幅值微小的故障检测效果不佳.
针对以上问题并结合之前的工作,本文提出改进的近邻保持嵌入算法(EWMA-DNPE),根据样本点邻域密度来动态地调整邻域参数的取值,同时结合指数加权移动平均(EWMA)算法,累积历史故障信息,提高故障检测率.
1 NPE算法介绍
NPE算法本质上是局部线性嵌入算法的线性近似,既有线性方法计算简便、可延展的优点,又兼具非线性流形学习的能力,能够克服流形学习算法存在的样本外点问题.
设X={xi∈RD,i=1,2,…,N}表示高维输入空间,NPE算法的目标是寻找最佳投影矩阵A(A∈RD×d,d (1)寻找近邻点 使用k近邻法(KNN),通过计算原始高维数据中各个数据点之间的欧氏距离,根据距离确定样本点xi最近的k个样本点作为其邻域点. (2)重构权值矩阵 通过近邻点线性重构每个数据点xi,并计算此样本点的重构权值矩阵W,使得重构误差最小, (1) (3)建立目标函数 保持权值不变,在低维空间重构原数据样本点,并使得重构误差最小化, (2) (4)获取低维投影矩阵 利用Y=ATX将目标函数化为 =YT(I-W)T(I-W)Y =YTMY (3) 其中,对称矩阵M=(I-W)T(I-W).利用拉格朗日方法,将目标函数的最小化问题化为求解如下广义特征值的问题,其最小的d个特征值(λ1≤λ2,…,≤λd)所对应的特征向量(ai,i=1,…,d)组成投影矩阵A=[a1a2,…,ad]. XMXTai=λXXTai (4) NPE算法中近邻点个数k的人工选取对算法性能有着很大的影响,较大的k值会导致流形的过平滑,而较小的k值则可能造成子流形的错误划分.为克服k值的人工设定问题,本文提出一种动态NPE算法(DNPE),根据样本点邻域密度来动态地调整k的取值.即流形上采样密度低的样本点的近邻点应少些,而采样密度高的样本点的近邻点应多些. (1)动态近邻参数选取 1)选择近邻参数的初始值k以及可能的最小值kmin和最大值kmax(k∈[kmin,kmax]).取值范围与实际问题有关,一般可选为kmin>d,kmax=80. 2)计算每个样本点xi的k个近邻Nk(xi)={xi1,xi2,…,xik},则xi与其近邻点的平均距离为 (5) 初始整体流形结构的平均距离为: (6) 则样本点xi的动态近邻参数为: (7) 若ki超出[kmin,kmax],则相应地选为kmin或kmax.从式(7)可以得出,di越小表明邻域数据点越密集,近邻点数相应越多,di越大表明邻域数据点越稀疏,近邻点数相应越少.这样就避免了非近邻成为重构点及近邻点未参与重构而造成的投影偏差. (2)动态重构权值矩阵 若动态近邻数ki>k,则保留Nk(xi)中所有近邻点,并选择Nkmax(xi)范围内的ki个近邻点,即将ki-k个点加入新的动态近邻集Nki(xi)中.若动态近邻数ki 通过近邻集中的点线性重构每个数据点xi,计算此样本点的重构权值矩阵W,使重构误差最小: (8) 此时,权值矩阵W与标准NPE算法有很大不同,标准算法中W的每一列都有且仅有k个非零元素,但是改进的NPE算法中W的每一列非零元素不同,即W的第i列有且仅有ki个非零元素. 其余步骤与标准NPE相同. 指数加权移动平均(EWMA)通过对历史数据进行加权操作,使得过去数据对当前时刻数据按照不同的权值产生影响,构造出一组新的时间相关的数据.因此,本文将EWMA与DNPE相结合,通过构建SPE统计量实现针对多变量时间序列的微小故障检测. 设第i时刻的采样数据为xi,则第i时刻构造的数据zi表示为: zi=λxi+(1-λ)zi-1 (9) 其中遗忘因子λ的取值范围是0~1,λ越小,过去时刻数据对当前时刻数据的影响就越大,递推可得: (10) 建模后,SPE统计量及其控制限计算公式如下: (11) (12) 若从第i(0 (13) xf=x*+lξ (14) 其中,xf表示样本向量,x*表示正常状态下的测量向量.令C=I-AAT,此时式(14)可化为 ≥δ (15) 并且有 (16) 所以有 (17) 此时临界可检测幅值l′为 (18) 其中Θ(·)表示矩阵的最大特征值,由式(18)可以看出,λ越小,基于SPE统计量的临界故障幅值则越小.只有当故障幅值大于临界可检测幅值l′时,DNPE算法才能利用SPE统计量及其控制限检测到故障.EWMA的引入降低了基于SPE统计量的临界故障幅值,提高了EWMA-DNPE算法对微小故障的检测效率. 离线建模过程: 1)获取历史采样数据并进行标准化处理; 2)选取合适的遗忘因子,利用EWMA重构样本数据; 3)利用改进的NPE对新的样本数据进行降维; 4)利用公式(4)和(12)计算降维的映射矩阵A和SPE统计量及其控制限. 本文中α设置为99%.当SPE小于控制线SPEα时,说明系统运行正常. 在线检测过程: 1)对当前时刻采样值进行标准化处理并利用EWMA进行数据重构; 2)利用建模过程步骤(4)获得的映射矩阵将数据投影到低维空间,并计算SPE统计量; 3)利用统计量是否超出控制限实现故障检测. 本文使用的数据均来自于SIMULINK仿真平台,该仿真平台主要由7个模块构成:控制器模块、四斜装飞轮轮系模块、三轴磁力矩器模块、三轴恒星敏感器模块、陀螺系统SHA模块、环境&轨道计算模块和卫星姿态解算(动力学&运动学)模块.仿真平台信号流图如图1所示. 图1 仿真平台信号流图Fig.1 Simulation platform signal flow diagram 故障A: θf(t)=θ0+Δθf,Δθf=0.002 5 rad,40 (19) 故障B: Δθf(t)=0.003cos(0.6t)rad,40 (20) 故障C: nf(t)=n0+Δnf,Δnf=10 r/min,150 (21) 故障D: Δnf(t)=15sin(60t)r/min,150 (22) 首先利用正常样本建立检测模型,包括不同近邻参数的NPE模型和EWMA-DNPE模型.将主元贡献率设定为85%,通过主成分分析法确定主元个数为3,相应地将NPE和EWMA-DNPE模型设定相同的降维维数.SPE统计量的统计置信度设置为99%,此时计算得到SPE统计量的控制限分别为1.23 和0.49. 表2列出了EWMA-DNPE方法对4种故障的检测结果,包括故障误报率(FAR)和漏报率(MAR).相比于传统的NPE方法,EWMA-DNPE方法在4种故障上都取得了更好的检测效果.图2和图3列出了不同近邻参数情况下的NPE模型和EWMA-DNPE对故障A和故障D的详细检测情况. 表2 EWMA-DNPE方法对4种故障的检测结果Tab.2 EWMA-DNPE method test results for 4 failures 如图2(a)(b)(c)所示,当故障幅值非常微小时,传统的NPE方法几乎不可能检测到故障,而且经典的NPE方法的检测效果十分依赖于近邻参数k,k的取值极大地影响到检测效率.当k值过小时,高维空间中的样本点重构误差增大,从而影响检测效果.当k值过大时则会导致信息冗余,增加算法时间复杂度(见表4).从图2(d)(e)可以看出,指数加权移动平均算法提高了算法对微小故障的检测效率,EWMA-DNPE的检测性能优于传统NPE方法. EWMA方法中遗忘因子λ的取值对EWMA-DNPE方法的故障检测效果有很大影响.随着λ的减小,正常数据的波动趋于平缓,EWMA-DNPE方法对于微小故障的检测将更加有效.然而,如果λ过小,则可能引入严重的时延从而影响故障检测的结果.在本文中,根据表3的结果,λ选为0.01,当λ选取过大时,算法不能有效检测到故障,故障漏报率很高,随着λ的减小,故障漏报率不断降低,当λ<0.01时,由于引入的时延导致漏报率反而上升. 故障D描述的是卫星姿态控制系统的执行器发生缓变故障的情况,模拟动量轮轴承润滑不良,摩擦力矩增大导致的动量轮转速异常. 由图3(a)和(b)(c)中可以看出,经典的NPE方法对故障D的检测结果不理想,几乎不能检测出故障,与故障A的检测结果比较可以得出缓变偏差的检测效果不如常值偏差.近邻参数k的取值仍然影响着NPE的检测结果,改进的NPE算法更具优越性. 图3(c)(d)和(e)的结果也表明,利用EWMA处理数据有效提升了算法对微小故障的检测性能. 图2 故障A的检测结果图Fig.2 Fault A test results 图3 故障D的检测结果图Fig.3 Fault D test results 遗忘因子λMAR0.867.50%0.530.00%0.13.75%0.012.50%0.0055.00% 表4 NPE和EWMA-DNPE的仿真时间Tab.4 NPE和EWMA-DNPE simulation time 本文在NPE局部流形结构学习的基础上,提出了一种用于卫星姿态控制系统微小故障检测的新方法.针对NPE算法中近邻参数选取困难和故障幅值偏小的问题,EWMA-DNPE方法考虑样本点邻域密度的影响,根据样本密度调整每个样本的近邻数,同时利用EWMA对故障的累积作用提高了微小故障的检测效率.仿真结果表明,与经典NPE方法相比,EWMA-DNPE方法在故障检测上具有令人满意的效果.需要注意的是,遗忘因子λ的选择将对EWMA-DNPE方法的检测效果产生影响. 参 考 文 献 [1] TUDOROIU N, KHORASANI K. Fault detection and diagnosis for satellite’s attitude control system (ACS) using an interactive multiple model (IMM) approach[C]//Conference: Control Applications. Toronto:2005: 1287-1292. [2] HUGHH T S,PENG J B. Fault detection, diagnosis, and fault tolerant control with flight applications[J]. Frankl. Inst. 2013:2371-2372. [3] 张森, 石军, 王九龙. 卫星在轨失效统计分析[J]. 航天器工程, 2010,19(4):41-46. ZHANG S,SHI J,WANG J L. Satellite on-board failure statistics and analysis[J]. Spacecraft Engineering, 2010,19(4):41-46. [4] 闻新, 张兴旺, 秦钰琦,等. 国外航天器在轨故障模式统计与分析[J]. 质量与可靠性, 2014(6):13-18. WEN X, ZHANG X W, Qin Y Q. Statistics and analysis on the failure mode of foreign spacecraft[J]. Quality and Reliability, 2014(6):13-18. [5] 刘豪.2011年国外航天故障综述[J]. 国际太空, 2012(2):48-55. LIU H. Summary of foreign spacecraft faults in 2011[J]. Space International, 2012(2):48-55. [6] 陈业, 胡昌华, 周志杰,等. 一种改进的SR—CDKF算法及其在早期微小故障检测中的应用[J]. 自动化学报, 2013, 39(10):1703-1713. CHEN Y,HU C H,ZHOU Z J, et al. Method of improving square-root center difference kalman filter with application to incipient failure detection[J].Acta Automatica Sinica, 2013, 39(10):1703-1713. [7] 李娟, 周东华, 司小胜,等. 微小故障诊断方法综述[J]. 控制理论与应用, 2012, 29(12):1517-1529. LI J,ZHOU D H, SI X S, et al. Review of incipient fault diagnosis methods[J].Control Theory & Applications, 2012, 29(12):1517-1529. [8] 文成林, 吕菲亚, 包哲静,等. 基于数据驱动的微小故障诊断方法综述[J]. 自动化学报,2016, 42(9):1285-1299. WEN C L, LYU Y F, BAO Z J, et al. a review of data driven-based incipient fault diagnosis[J]. Acta Automatica Sinica, 2016, 42(9):1285-1299. [9] ZHOU W. Incipient bearing fault detection for electric machines using stator current noise cancellation[D]. Georgia Institute of Technology, 2007. [10] SARAVANAN N, RAMACHANDRAN K I. Incipient gear box fault diagnosis using discrete wavelet transform (DWT) for feature extraction and classification using artificial neural network (ANN)[J]. Expert Systems with Applications, 2010, 37(6):4168-4181. [11] SAI K P, ADITHYA R, BALASUBRAMANIAN N, et al. A novel data fusion method for incipient fault detection in tru of aircraft electrical system[J]. Proceedings of the National Academy of Sciences of the United States of America, 2014, 81(20):6305-9. [12] 尚骏, 陈茂银, 周东华. 基于变元统计分析的微小故障检测[J]. 上海交通大学学报, 2015, 49(6):799-805. SHANG J, CHEN M Y, ZHOU D H. Incipient fault detection using transformed component statistical analysis[J]. Shanghai Jiaotong Daxue Xuebao/journal of Shanghai Jiaotong University, 2015, 49(6):799-805, 811. [13] SU L, SHANG C X, SU Y,et al. Fault detection and isolation based on multivariate statistical analyzing for the satellite attitude control system[C]//Proceedings of International Conference on Electronic Measurement Instruments. Beijing:2009,884-889. [14] DING S, ZHANG P, DING E, et al. On the application of pca technique to fault diagnosis[J]. Tsinghua Science & Technology, 2010, 15(2):138-144. [15] LI L Y, WANG X M, MU L X. incipient fault detection for a hypersonic scramjet vehicle[J]. Lecture Notes in Electrical Engineering, 2014, 296:31-38. [16] FUJIMAKI R, YAIRI T, MACHIDA K. An approach to spacecraft anomaly detection problem using kernel feature space[C]//Eleventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, Illinois, Usa, August. 2005:401-410. [17] MIAO A M,SONG Z H, GE Z Q,et al.Nonlinear fault detection based on locally linear embedding[J].Control Theory Apply, 2013, 11(4):615-622. [18] CHENG Y, JIANG B, LU N, et al. Incremental locally linear embedding-based fault detection for satellite attitude control systems[J].Journal of the Franklin Institute, 2015, 353(1):17-36. [19] 郑茜予. 基于主元分析的微小故障检测[D]. 北京: 华北电力大学, 2015. ZHENG X Y. incipient fault detection based on principal component analysis[D].Beijing: North China Electric Power University,2015. [20] 邱天, 白晓静, 郑茜予,等. 多元指数加权移动平均主元分析的微小故障检测[J]. 控制理论与应用,2014, 31(1):19-26. QIU T, BAI X J, ZHENG X Y,et al. Incipient fault detection of multivariate exponentially weighted moving average principal component analysis[J]. Control Theory & Applications, 2014, 31(1):19-26. [21] LIU M, LU N, CHENG Y, et al. Data-based incipient fault detection and prediction for satellite’s attitude control system[C]//Control and Decision Conference. Chongqing:IEEE, 2017:1202-1207.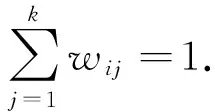
2 基于EWMA-DNPE的微小故障检测
2.1 DNPE算法步骤
2.2 微小故障可检测性分析

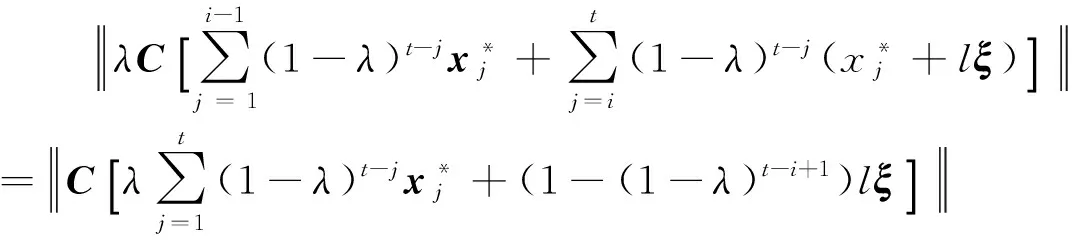
2.3 基于EWMA-DNPE的故障检测步骤
3 方法验证
3.1 仿真系统平台



3.2 仿真结果





4 结 论
