适用于时变不确定系统的并行模型自适应估计*

熊 凯，魏春岭，刘良栋

0 引 言

传统卡尔曼滤波(KF)算法的性能会受到模型不确定性的影响，需要通过改善滤波器的设计提升状态估计的鲁棒性.很多带有动力学或测量特性不确定性的系统，都可以用带有不确定性参数的模型来描述.利用扩维卡尔曼滤波(AKF)算法将状态变量和不确定性参数一起进行估计，是削弱模型不确定性影响的有效途径之一.在不确定性参数持续存在并且能够得到准确估计的情况下，应用AKF代替传统KF有助于提升滤波性能.但是，对于很多工程系统，受环境因素和认知水平的制约，模型不确定性的影响是潜在的，不确定性参数出现的时间及其幅度是事先未知的.在模型不确定性不出现的情况下，受不确定性参数估计不准确等因素的影响，AKF的性能反而不如传统KF.基于不确定性模型设计的AKF在出现模型不确定性的情况下能够体现出较强的鲁棒性，然而，在模型准确的情况下，其性能往往是次优的.很难设计一个单独的滤波算法，使其在模型不确定性出现和不出现两种情况下，都能达到理想的滤波性能.

利用多模型自适应估计(MMAE)的理论方法，基于多个模型设计多个并行滤波器，可以提升滤波算法对于不同环境的适应能力.多模型自适应估计算法中包含一系列并行滤波器，每个并行滤波器基于模型集中的一个模型进行设计，用于提供各自的状态估计值，MMAE算法的输出是各个并行滤波器估计值的加权和；对应各个并行滤波器的权值根据相应的测量新息计算得到，反映了模型集中的各个模型与实际系统的相似程度.MMAE算法自提出以来，受到了学术界的广泛重视，并针对多个工程系统开展了应用研究[1-4].在以往的工作中，多模型滤波算法已用于处理模型不确定性[5-8].但是，传统的处理方法要求建立完备的模型集，通常要求模型集具有精细的网格结构，以保障不确定性参数描述的准确程度，并覆盖参数的取值范围；同时，又要求模型集的规模不能太大，尽量避免增大算法的计算量.上述两种要求是相互矛盾的，给MMAE算法的空间应用造成了限制.

本文主要贡献在于：针对系统中潜在不确定性的影响，提出一种基于KF和AKF自适应切换的PMAE算法，其中，KF算法基于正常情况下的精确模型进行设计，而AKF算法基于带有不确定性参数的模型进行设计.PMAE算法可以根据当前应用环境的不同，充分发挥KF和AKF各自的优势，使得整个算法在模型不确定性存在和不存在两种情况下，都能取得令人满意的性能表现.以空间目标监视为例，PMAE算法在应对非合作目标运动潜在的状态突变时，能够达到优于传统算法的估计精度；并且，实施该算法最少仅需要建立两个并行滤波器，适用于星上计算资源受限的情况.

1 系统模型

考虑如下所示的时变不确定系统：

xk=Fkxk-1+DkΔk+wk

(1)

yk=Hkxk+Gkθk+vk

(2)

其中，k表示离散的时间，xk为状态变量，yk为观测量，wk表示系统噪声，vk表示测量噪声，Fk为状态转移矩阵，Dk是未知输入Δk的增益阵，Hk是观测矩阵，Gk是测量偏差θk的增益阵，未知参数向量Δk和θk可视为模型不确定性.假定wk和vk为不相关的零均值白噪声向量，其方差阵分别为Qk和Rk，假定式中的向量和矩阵具有适当的维数.

KF是实现系统状态估计的传统方法，对于精确模型(Δk=0,θk=0)，KF能够利用一个时段上的观测序列{y1,y2,…,yk}得到状态变量xk的最优估计.KF算法的每次迭代计算包含两个环节，即预测和更新.在预测环节，根据如式(1)所示的动力学模型对状态变量进行预测；在更新环节，先根据观测方程(2)计算预测观测量与实际观测量之差，即测量新息，进而，将测量新息与滤波增益的乘积用于修正状态预测值，得到这一步的状态变量估计值.在系统中不存在模型不确定性的情况下，利用KF能够达到理想的估计精度.但是，存在模型不确定性的情况下，不确定性参数向量Δk和θk会对预测和更新过程产生不利影响，从而影响到最终的状态估计结果.

2 滤波方程

MMAE算法可用于处理模型不确定性，传统方法是构建由多个模型组成的模型集，用于描述不确定性参数向量Δk和θk.对于通常的物理系统，不确定性参数向量的各个元素是有界的，因此，可在固定区间内取M个样本，形成多维网格结构，作为不确定性参数向量的数学描述.接下来，建立M个并行滤波器，每个并行滤波器基于模型集中的一个模型进行设计，通过设计自适应率，使得最接近实际系统的模型在状态估计中起主导作用，从而消除模型不确定性的影响，取得令人满意的状态估计结果.显然，模型集中网格的间距越小，对不确定性参数向量进行描述的精细化程度就越高，同时算法的计算量也越大.对于高维系统，传统MMAE算法的计算效率往往较低.

为了减小算法的计算量，本文提议仅利用两个模型进行设计，在第1个模型中，假定不确定参数向量Δk和θk为零；在第2个模型中，将Δk和θk扩充为状态，用于进行估计.第1个模型适用于系统中未出现模型不确定性的情况，而第2个模型适用于系统中出现模型不确定性的情况.相应地，针对两个模型分别设计KF和AKF算法，作为PMAE的两个并行滤波器；通过两个滤波器的并行解算和加权融合获得总的状态估计.PMAE算法的实施步骤如下所示：

第1步：初始化

第2步：并行滤波

两个并行滤波器分别对状态变量估计值进行预测和更新，第1个并行滤波器基于KF进行迭代计算，滤波方程为

(3)

(4)

第2个并行滤波器基于AKF进行迭代计算，滤波方程为

(5)

(6)

桥隧施工及养护课程是铁道工程技术专业的一门专业核心课程，该课程要求学生掌握桥涵隧构造、施工方法、养护维修知识。我国大多数院校，在这门课程教学中，由于教师力量和实训室建设的局限，理论讲授比重大，很难做到“教学做”相结合，教学过程枯燥。教材内容相对落后。这导致学生对课程的参与度低，学生兴趣不高，教学效果一般。

第3步：权值更新

各个并行滤波器的权值根据测量新息进行计算，并进行归一化，该过程的数学表达式为

(7)

(8)

第4步：加权融合

PMAE算法总的状态估计值是各个并行滤波器状态估计值的加权和，即

(9)

3 空间目标监视

空间目标监视系统可用于在轨服务、碎片治理和威胁预警等，需要解决的基本问题是确定空间目标的位置和速度等运动状态[9-10].对于远距离非合作目标，可通过安装在观测卫星上的照相观测星相机提供空间目标的视线(LOS)矢量测量信息，并通过轨道动力学模型对空间目标的运动状态进行预测.对空间目标实施双LOS矢量观测，能够增强观测量对空间目标位置的几何约束，增强监视系统性能.应当说明，在观测期间，非合作目标可能会实施轨道机动，对于观测卫星而言，目标机动的开始时刻、持续时间和幅度大小均是未知的.

(10)

(11)

其中，μ是地心引力常数，p(rt)用于描述除地球中心引力场之外，其他轨道摄动对空间目标运动的影响，通常包括地球形状摄动、日-月引力摄动、大气阻力摄动和太阳光压摄动等，ut是空间目标发动机推力引起的未知加速度，在此建模为不确定性参数向量的形式.

测量模型可写为

(12)

其中，ro1和ro2分别表示观测卫星中主星和辅星的位置矢量，假定观测卫星的位置矢量是精确已知的.tk表示根据主观测卫星星上时钟得到的观测时间，Δtjk(j=1,2)表示光从空间目标传播到观测卫星所需的时间.考虑到空间目标监视系统的动力学模型和观测模型都是非线性的，可以采用非线性系统线性化的技术设计PMAE算法中的各个并行滤波器.

4 仿真分析

空间目标和观测卫星的真实轨道数据通过高精度轨道仿真器计算得到，假定它们均在高度约1 000 km、倾角约63°的近圆轨道上运行，星间距离在100～200 km范围内变化.假定观测卫星的位置误差标准差为10 m，安装在观测卫星上的照相观测星相机每秒采样1次，空间目标视线方向测量噪声的标准差为5″.假定空间目标的重量为1 000 kg，安装在空间目标上的星载发动机推力标称值为100 mN，空间目标轨道机动的时间和幅度对于观测卫星而言是事先未知的.

基于给定的初始值，通过高精度轨道外推得到标称轨道数据，并根据观测模型计算得到观测序列；利用滤波算法对仿真模拟得到的观测序列进行处理，通过迭代计算得到状态变量的估计值.将状态变量的估计值与标称数据进行比对，得到空间目标的位置估计误差曲线及其统计值.

利用不同滤波算法处理同一组测量数据，通过数学仿真对比了KF、AK、MMAE和PMAE这4种算法的性能.在KF算法的设计过程中，未考虑空间目标推力加速度ut的影响.在AKF算法中，将不确定性参数矢量ut扩充为状态，与空间目标的位置矢量和速度矢量一起进行估计.显然，KF适用于目标未进行轨道机动的情况，而AKF适用于目标进行轨道机动的情况.基于文献[11]中的描述进行MMAE算法的设计，MMAE基于两个并行KF进行，在第1个KF中，系统噪声方差阵取为标称值，在第2个KF中，人为将系统噪声方差阵的标准差扩大100倍.在PMAE算法中，第1个并行滤波器基于KF进行设计，第2个并行滤波器基于AKF进行设计.

在仿真过程中，空间目标执行轨道机动的情况下，利用KF和PMAE算法得到的位置估计误差曲线分别如图1～2所示.

图1 存在轨道机动情况下的KF位置估计误差曲线Fig.1 Estimation error of KF in the presence of maneuver

图2 存在轨道机动情况下的PMAE 位置估计误差曲线Fig.2 Estimation error of PMAE in the presence of maneuver

为了便于进行对比分析，将KF、AKF、MMAE和PMAE 4种算法的位置估计误差均方根归纳在表1中.存在模型不确定性的情况下，PMAE算法能够实现对空间目标未知加速度的补偿，其性能优于KF；基于方差放大技术设计的MMAE算法在方差阵设计满足应用要求的情况下，也具备部分削弱空间目标轨道机动影响的能力.

空间目标未执行轨道机动的情况下，PMAE算法的位置估计误差曲线如图3所示，相应的权值收敛曲线如图4所示.正如所期望的，对应KF的并行滤波器的权值收敛于1，对应AKF的并行滤波器的权值收敛于0.因此，KF在PMAE估计中起主导作用.

图3 不存在轨道机动情况下的PMAE 位置估计误差曲线Fig.3 Estimation error of PMAE in the absence of maneuver

图4 不存在轨道机动情况下的PMAE权值收敛Fig.4 Weight convergence for PMAE in the absence of maneuver

受敏感器随机误差等因素的影响，此时AKF中对ut的估计不严格为0，相当于在轨道外推过程中引入了误差，对位置估计产生了不利影响.根据表1易知，PMAE算法的估计精度优于AKF，KF、MMAE和PMAE的精度水平近似一致.PMAE算法中不同仿真条件下的良好表现，使其成为空间目标监视系统滤波器设计的一种理想备选方案.

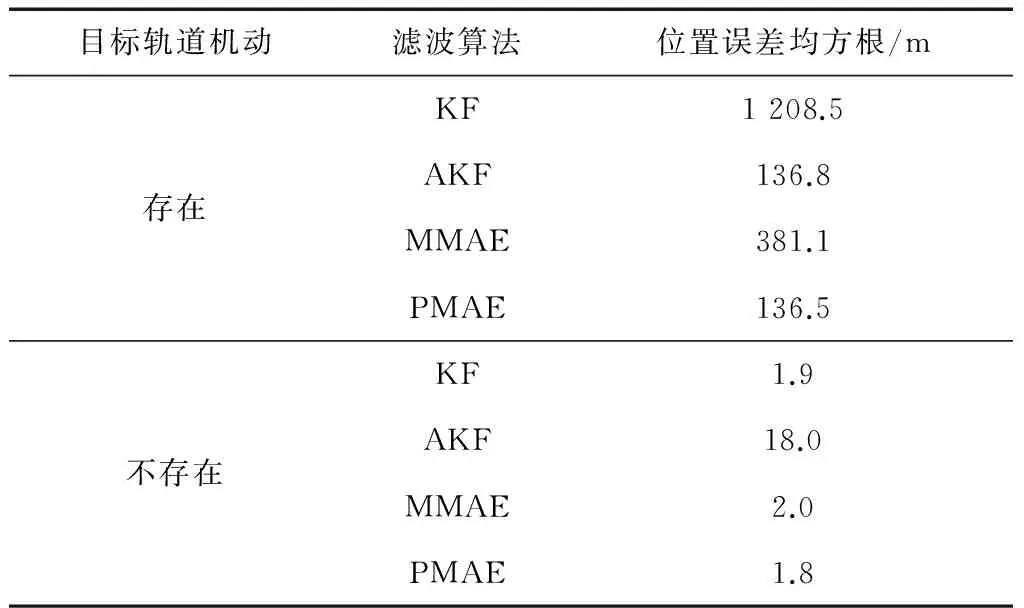
表1 空间目标监视不同滤波算法性能比较Tab.1 Comparison of filtering performance for space surveillance

5 结 论

本文提出一种基于KF和AKF相结合的并行模型自适应估计算法，其中，KF算法适用于模型精确的情况，而AKF算法适用于模型中存在不确定性参数的情况.基于上述设计，PMAE算法在系统中存在模型不确定性和不存在模型不确定性两种情况下，均能自适应的选择适当的滤波算法进行处理，从而取得理想的滤波性能.通过数学仿真验证了算法的有效性，仿真结果表明，所提算法能够根据应用环境的不同选择不同的并行滤波器占主导地位，达到了预期的设计效果.

参 考 文 献

[1] GAO C, DUAN G.Fault diagnosis and fault tolerant control for nonlinear satellite attitude control systems[J].Aerospace Science and Technology, 2014,33(1):9-15.

[2] YU N J, RYOO C K.Missile guidance law estimation using modified interactive multiple model filter[J].Journal of Guidance, Control, and Dynamics, 2014,37(2):484-496.

[3] YIN Z G,ZHAO C,ZHONG Y R,et al.Research on robust performance of speed-sensorless vector control for the induction motor using an inferfacing multiple-model extended Kalman filter[J].IEEE Transactions on Power Electronics,2014,29(6):3011-3019.

[4] XIONG K, WEI C L, LIU L D.Robust multiple model adaptive estimation for spacecraft autonomous navigation[J].Aerospace Science and Technology,2015,42:249-258.

[5] ALSUWAIDAN B N, CRASSIDIS J L, CHENG Y.Generalized multiple-model adaptive estimation using an autocorrelation approach[J].IEEE Transactions on Aerospace and Electronic Systems, 2011,47(3):2138-2152.

[6] HAMMES U, ZOUBIR A M.Robust MT tracking based on M-estimation and interacting multiple model algorithm[J].IEEE Transactions on Signal Processing, 2011,59(7):3398-3409.

[7] LI W,JIA Y,DU J,et al.Distributed multiple-model estimation for simultaneous lo-calization and tracking with NLOS mitigation[J].IEEE Transactions on Vehicular Technology,2013,62(6):2824-2830.

[8] LAN J,LI X R.Equivalent-model augmentation for variable-structure multiple-model estimation[J]. IEEE Transactions on Aerospace and Electronic Systems,2013,49(4):2615-2630.

[9] PSIAKI M L.Absolute orbit and gravity determination using relative position measurements between two satellites[J].Journal of Guidance, Control, and Dynamics, 2011,34(5):1285-1297.

[10] CHEN T, XU S.Double line-of-sight measuring relative navigation for spacecraft autonomous rendezvous[J].Acta Astronautica, 2010, 67:122-134.

[11] XIONG K,WEI C L.Multiple model adaptive estimator for nonlinear system with unknown disturbance[J].Asian Journal of Control,2015,17(6):2252-2262.