轨控大干扰下的系统角动量管理*

王淑一，雷拥军，王新民，袁 军

0 引 言

为满足载荷工作要求，需要从升(降)交点地方时、地面覆盖、编队飞行等方面保持航天器的轨道特性，在航天器入轨初期和在轨运行期间，对轨道进行调整[1].轨道控制就是通过利用或主动对航天器施加外力改变航天器质心运动的轨迹，调整轨道使其沿要求的轨道运行[2].从易于工程实施的角度考虑，航天器的轨道控制通常分为轨道平面内、轨道平面外变轨控制两大类.

为实现轨道控制目标，通常需要姿态控制相配合[3]，在轨道控制过程中保证姿态指向，使得轨控推力器沿着指定方向提供速度冲量.由于受到轨控推力器安装偏差或者性能变化、航天器质心变化等因素影响，轨道控制期间会产生较大的干扰力矩，且干扰力矩一般呈现为单方向扰动较大的特性[4].考虑用于航天器姿态长期控制的角动量管理装置，如飞轮和控制力矩陀螺，存在控制力矩能力及角动量吸收容量的约束问题，因此轨道控制时多采用推力器进行姿态控制，以抑制轨控推力器工作时产生的姿态影响.当在轨航天器三轴姿态控制推力器由于部分异常或其它问题导致推力器无法使用、推力器无法提供三轴控制力矩时，则航天器成为喷气欠驱动控制系统[5-6]，在轨控大干扰下一般很难实现轨控期间的姿态维持控制.利用角动量管理装置实现轨控期间的姿态维持控制时，采用磁力矩器卸载方式，存在无法短时间内完成角动量管理装置的角动量卸载问题.

针对姿控推力器部分失效下的轨道控制期间姿态维持问题，本文结合轨控干扰力矩特性分析，基于配置的角动量管理装置提出了大干扰力矩下的轨控姿态维持控制及飞轮系统的角动量管理方法，可以为推力器失效的航天器轨控实现提供参考，也可以推广应用在无姿控推力器的轨道调整控制中.

1 基于角动量管理装置的姿态控制

对于配置角动量管理装置的刚体航天器，在干扰力矩下系统的动力学模型[7-8]为

(1)

式中:J为航天器惯量矩阵；ω=[ωxωyωz]T为航天器的绝对角速度在本体系下表示；hw为角动量管理装置系统合成角动量在本体系下表示；u为角动量管理装置的控制力矩在本体系下表示；τdis=[τdxτdyτdz]T为干扰力矩在本体系的表示.

航天器在对地稳定运行时，星体相对轨道坐标系的姿态一般采用欧拉角描述，对应的星体三轴欧拉姿态角分别记为φ,θ,ψ，通常称之为滚动角、俯仰角和偏航角，对应的航天器的绝对角速度ω可表示为

(2)

式中：ωbo为星本体相对轨道系的角速度；Cbo(φ,θ,ψ)为星本体相对轨道系的方向余弦阵；ωo为轨道角速率，对于近圆轨道可近似看作常数.

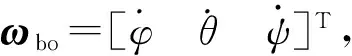
(3)

当选取控制量为

(4)

式中,ωn、ζn>0为选取的控制参数，其决定闭环系统动态特性.对于不同通道，可根据控制性能要求不同设计为不同参量，在本文中为了描述简洁，故三通道均设计为相同参量.

当采用式(4)控制形式时，由式(3)及式(1)可得闭环系统的动力学方程为:

(5)

2 轨控干扰下角动量管理装置系统的角动量管理

2.1 轨控干扰特性分析

航天器轨道控制包括轨道平面外控制和轨道平面内控制，其中前者主要用于倾角控制，后者主要用于轨道升降轨、偏心率及拱线控制等.对于轨道平面外控制，由于轨控推力矢量垂直轨道平面，轨控产生的扰动力矩为轨道平面内；对于轨道平面内控制，由于轨控推力矢量沿着或反向沿着航天器运行方向，轨控产生的扰动力矩在轨道平面或轨道法线方向均有可能.

当进行轨道平面内控制且轨控的主要干扰力矩在轨道平面外时，可通过航天器绕滚动轴旋转一定角度使得干扰力矩仅在轨道平面内，且可保证轨控推力矢量方向不变.因此，不失一般性，我们可假设轨控干扰力矩存在于轨道面内，且干扰仅存在于航天器本体系z轴方向，即τdis=[0 0τdz]T.需要注意的是此处本体系可能为卫星绕滚动轴转动后的本体系.

在轨控开始时刻(t=0)建立O-XYZ的惯性坐标系，该坐标系的XOZ平面选为轨道平面，则该惯性坐标系与星体本体坐标系O-XbYbZb关系如图1所示.

当仅存在星体+Zb方向的轨控干扰力矩时，从0到t的轨控时长内，其轨控干扰力矩产生的干扰角动量在惯性系下可表示为：

(6)

式中：Hx和Hz分别为干扰角动量在惯性系X轴和Z轴的分量；β为星本体系相对轨控起始时刻(t=0)的相位角.

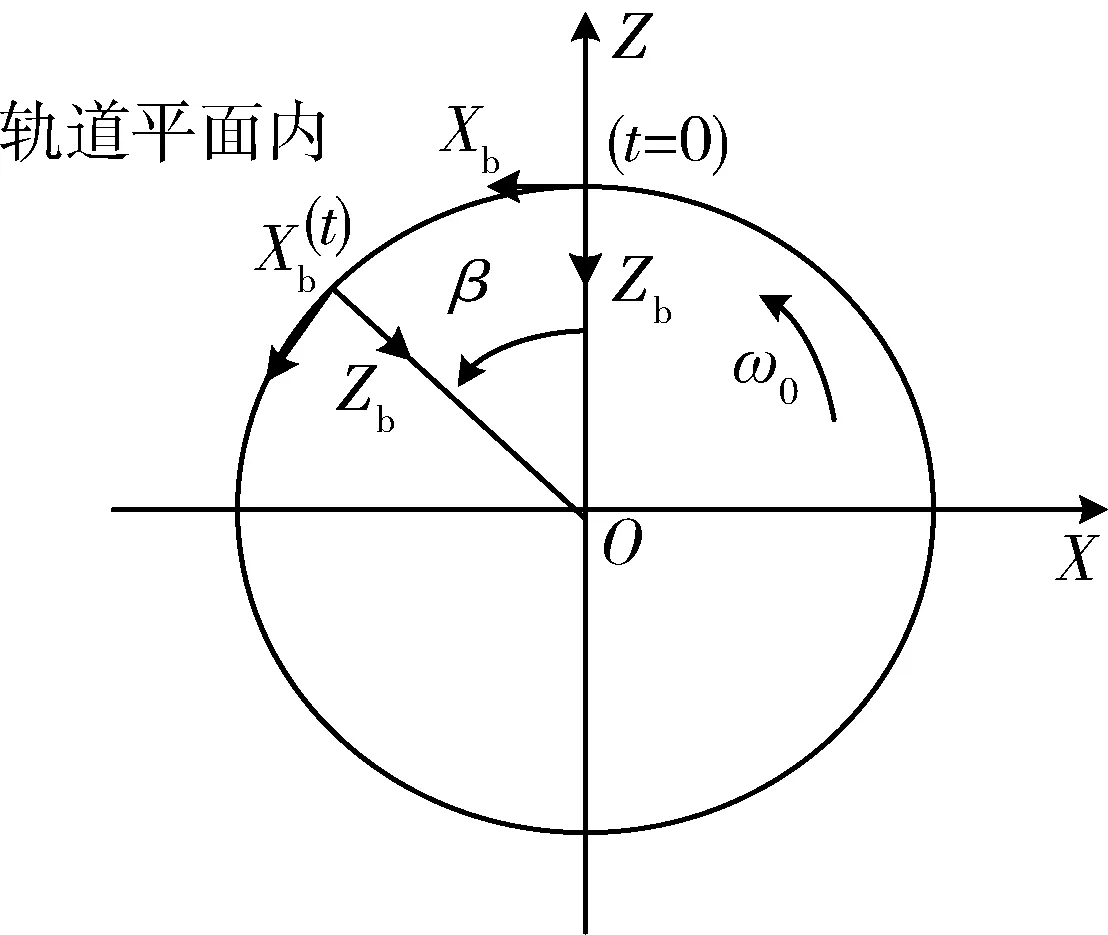
图1 惯性系与本体系的关系Fig.1 Relationship between the body frame and the inertial reference frame

由式(6)可知，轨控干扰力矩积累角动量具有如下性质：

1) 轨控干扰角动量在惯性系X方向围绕常值τdz/ωo呈现周期变化，变化周期为轨道周期：在1/2轨道周期时刻，即β=π时，积累角动量在惯性系X方向达到最大，其幅值为-2τdz/ωo，此时角动量方向为星体+Xb方向；

2) 轨控干扰力矩积累角动量在惯性系Z方向围绕常值0呈现周期变化，变化周期为轨道周期：在1/4和3/4个轨道周期时刻，积累角动量在惯性系Z方向达到最大，其幅值为τdz/ωo，其中1/4轨道周期时刻角动量沿星体的-Zb方向，3/4个轨道周期时刻角动量沿星体的+Zb方向.

2.2 基于角动量自平衡的角动量管理方法

根据轨控干扰特性分析结果，若轨控初始时刻在X轴方向建立-τdz/ωo的常值角动量偏置，则轨控干扰角动量在惯性系X方向和Z方向都表现为轨道周期特性，幅值均为τdz/ωo.在轨控初始时刻建立偏置角动量条件下，在惯性系下干扰角动量可表示为

(7)

利用角动量管理装置系统实现轨控下的姿态维持控制，若单次连续轨控时间过长则有可能超过系统角动量容量.此外，当干扰力矩幅值超过角动量管理装置提供的控制力矩幅值时，则会产生姿态偏差从而影响轨控效能.因此，在角动量管理装置实现轨控期间的姿态维持时，需要考虑系统角动量容量与容许的姿态偏差两方面约束.

在系统角动量容量约束下，轨控干扰积累角动量幅值不能超过设定幅值.设一个轨道周期内允许产生累积角动量HP(≤τdz/ωo)，则HP应小于系统可吸收的角动量范围Hwmax，于是可得轨控干扰力矩在一个轨道周期内允许作用的时间Tp应为满足

(8)

偏置角动量的建立可以利用轨控干扰实现.根据轨控干扰力矩方向，选取合适的轨道相位实施合适时长的轨道控制：以轨控干扰力矩τdz>0为例，若需在惯性系X轴方向建立负偏置角动量，则可选取β=-90°的相位点，此时轨控干扰可在-X方向产生累积角动量，建立起所需的偏置角动量HX0.

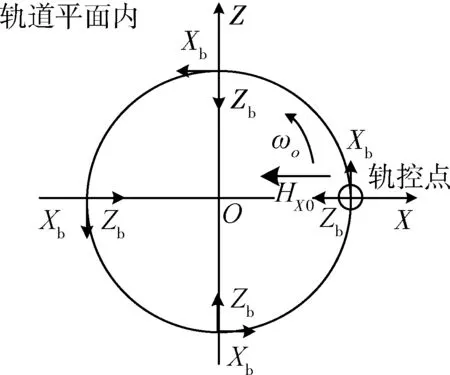
图2 偏置角动量建立示意图Fig.2 Schematic diagram of biased momentum establishment

在进行轨道面内控制，若仅进行轨道高度调整，为避免轨控过程对偏心率产生影响，可将连续轨控允许的作用时间Tp按照等间隔、均匀地分布在一个轨道周期内，即采取“对称点”控制方式.设计轨控次数M为

M=2N(N=1，2，……)

则单次轨控时间长度为

以N=2为例，建立起图2所示的X轴偏置角动量，取其角动量偏置值为HP/M，则之后轨控序列及其过程中角动量变化如下：

1)在第一次轨控点P0处，产生Z方向干扰角动量HP/M，控后星体角动量为

Hx=Hz=HP/M

2)在第二个轨控点P1处，控后角动量仅有

Hz=HP/M

3)以此类推，P2，P3处的角动量分别为0和Hx=HP/M，经过一个轨道周期4次轨控后，航天器恢复初始X方向偏置角动量的状态.

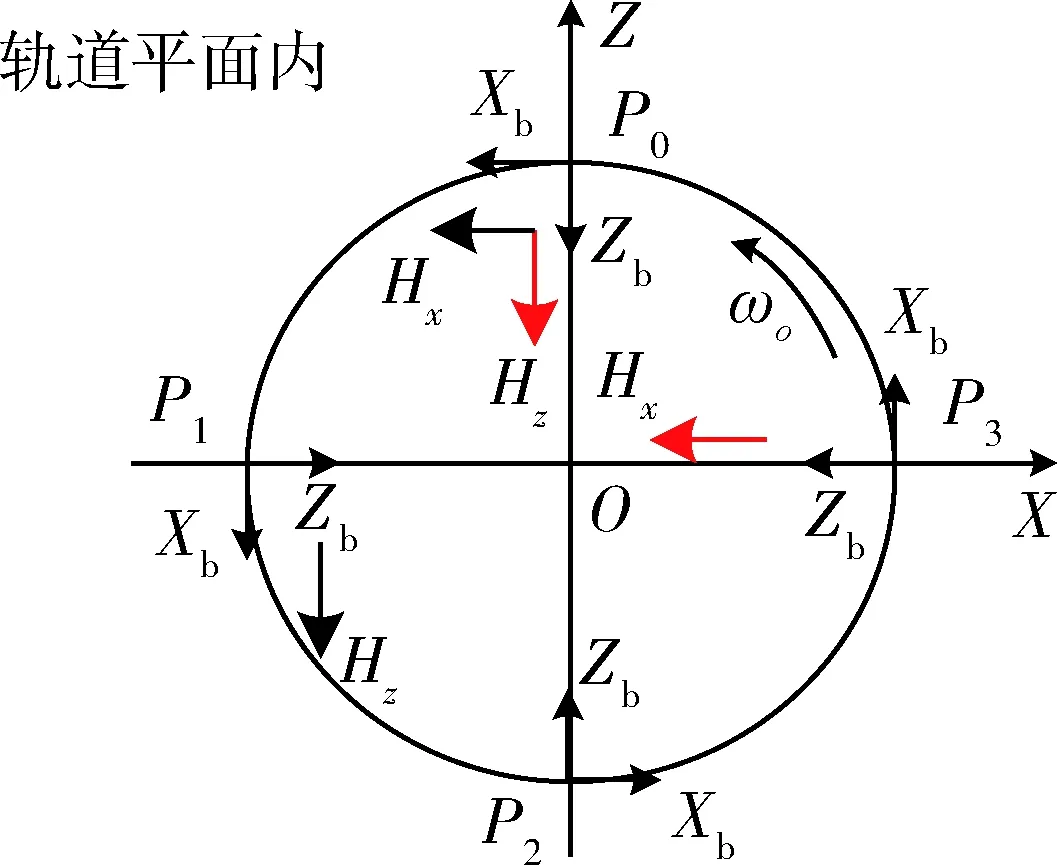
图3 轨控过程角动量变化情况Fig.3 Variation of accumulated momentum in orbit control stage

由此可见：该轨控策略通过合理利用惯性空间角动量不变原理，设计了一个轨道周期内的轨控序列，在不利用姿控推力器的前提下，实现轨控干扰角动量的管理.

当角动量管理装置系统提供的最大控制力矩τcmax远远大于干扰力矩τdz幅值时，则由式(5)偏航通道的闭环动力学方程的阶跃响应可知偏航轴姿态达到的最大值为

在轨控过程中，为保证轨控效能，一般姿态角偏差需小于轨控期间允许的偏差Δmax(一般设定Δmax≤5°).因此，选择控制参数ωn、ζn使得|ψmax|≤Δmax.为了使得角动量管理系统及时地吸收干扰力矩积累角动量且控制过程中姿态控制超调小，式(4)中的控制参数ωn、ζn尽量选取足够大的值.

对于飞轮控制系统，当其在各通道输出最大控制力矩τcmax小于干扰力矩幅值时，则姿态呈现发散趋势.忽略姿态控制在控制力矩饱和前的动态响应，则动力学方程式(1)的偏航通道可近似为双积分环节，在初始偏航姿态及姿态角速度近似为零的情况下，在单次轨控时长TPi结束时的姿态角及角速度幅值为

在上述情况下，单次连续轨控时长TPi选择还需使得姿态角偏差小于轨控允许偏差Δmax，即

3 仿真结果及应用效果

针对某低轨航天器入轨后+Zb方向推力器无法使用的情况[5]，航天器初始入轨轨道与目标轨道之间高度差为55 km，需要在飞轮系统进行姿态控制下实现轨道控制.为了解轨控推力器的干扰特性，在轨开展了轨控推力器间歇式短期工作，姿态控制采用三轴轮控方式，利用轮系角动量变化估计轨控干扰力矩.经试验和计算，某轨控推力器工作时在+Zb方向产生了0.25 N·m的干扰力矩，且干扰力矩幅值已经超过轮系最大控制力矩0.1 N·m范围.试验过程轨控推力器工作时长、轮系角动量以及三轴姿态变化见图4～6.

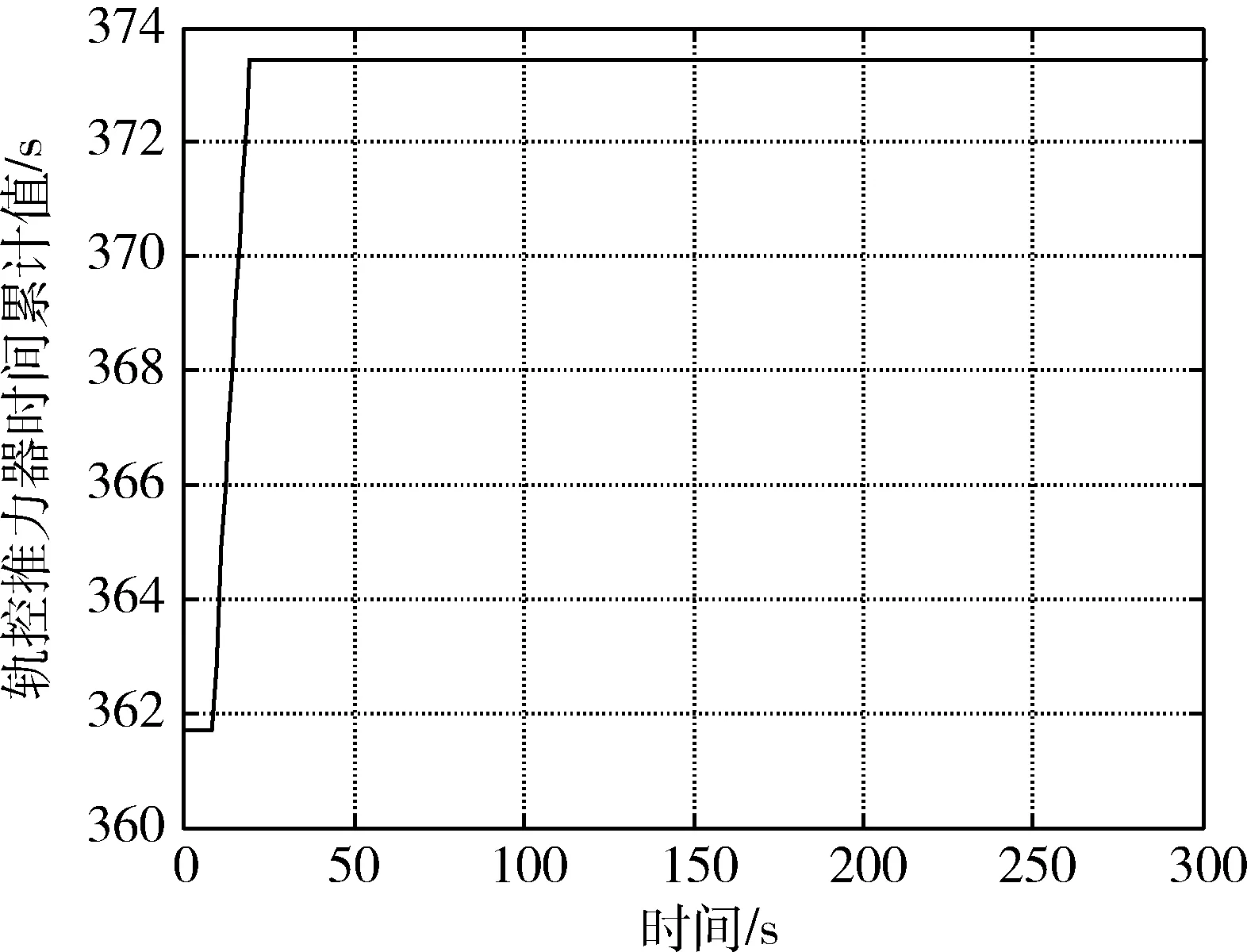
图4 轨控推力器工作时长变化曲线Fig.4 Firing duration of orbit jets in intermittent work mode

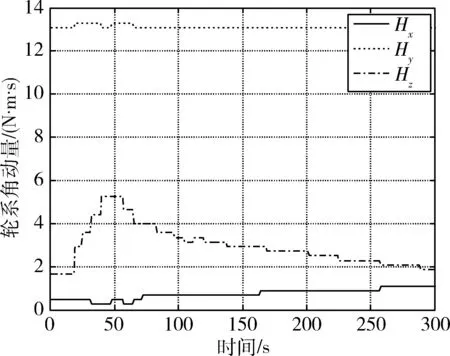
图5 飞轮系统角动量变化曲线Fig.5 Momentum of flywheels

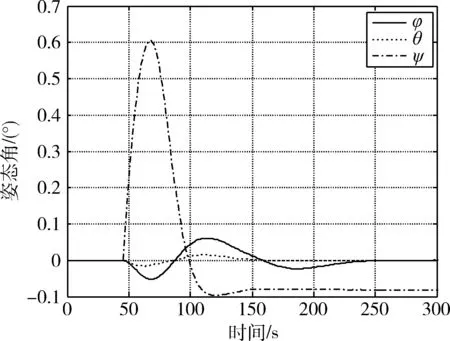
图6 三轴姿态角变化曲线Fig.6 Attitude angles

从在轨试验结果可知：本次试验中某轨控推力器工作时长约为13 s，飞轮系统吸收的角动量约为3.3 N·m·s，控制过程中三轴姿态角误差为0.6°，系统稳定.

按照第2节给出的角动量管理方法及轨控策略，考虑飞轮系统可吸收角动量小于8 N·m·s及轮系最大输出力矩0.1 N·m，为保证控制实现具有足够裕度，选取一个轨道周期内允许轨控时长Tp为20 s(极限值为100 s).

结合偏置角动量建立过程以及轨控策略，将偏置角动量建立过程与轨控过程相结合，设置第一个轨道周期内的4个轨控点的轨控时长分别为10 s，10 s，20 s，20 s.

另外，为提高航天器自主性，设计在轨自主执行每个轨道周期4次轨控的方案，为保证角动量在合理范围内，在数据分析基础上，通过当前角动量与目标角动量偏差自动调节单次轨控长度.设第一个轨控点P0对应的轨道幅角为u0，则后续轨控点分别为u0+90°、u0+180°、u0+270°，实时获取星上轮系的三轴角动量，计算出本次轨控时长为

其中HWzb为飞轮系统在本体系Z轴的角动量.

按照上述自主轨控策略，进行数学仿真验证.地面仿真中考虑轨控干扰力矩的不确定性，将轨控干扰力矩设置为常值0.5 N·m加上随机0.2 N·m(3σ)的变化，进行40 000 s数学仿真，自主执行25次轨控，单次轨控时长约为20 s.数学仿真结果如图8～10所示.

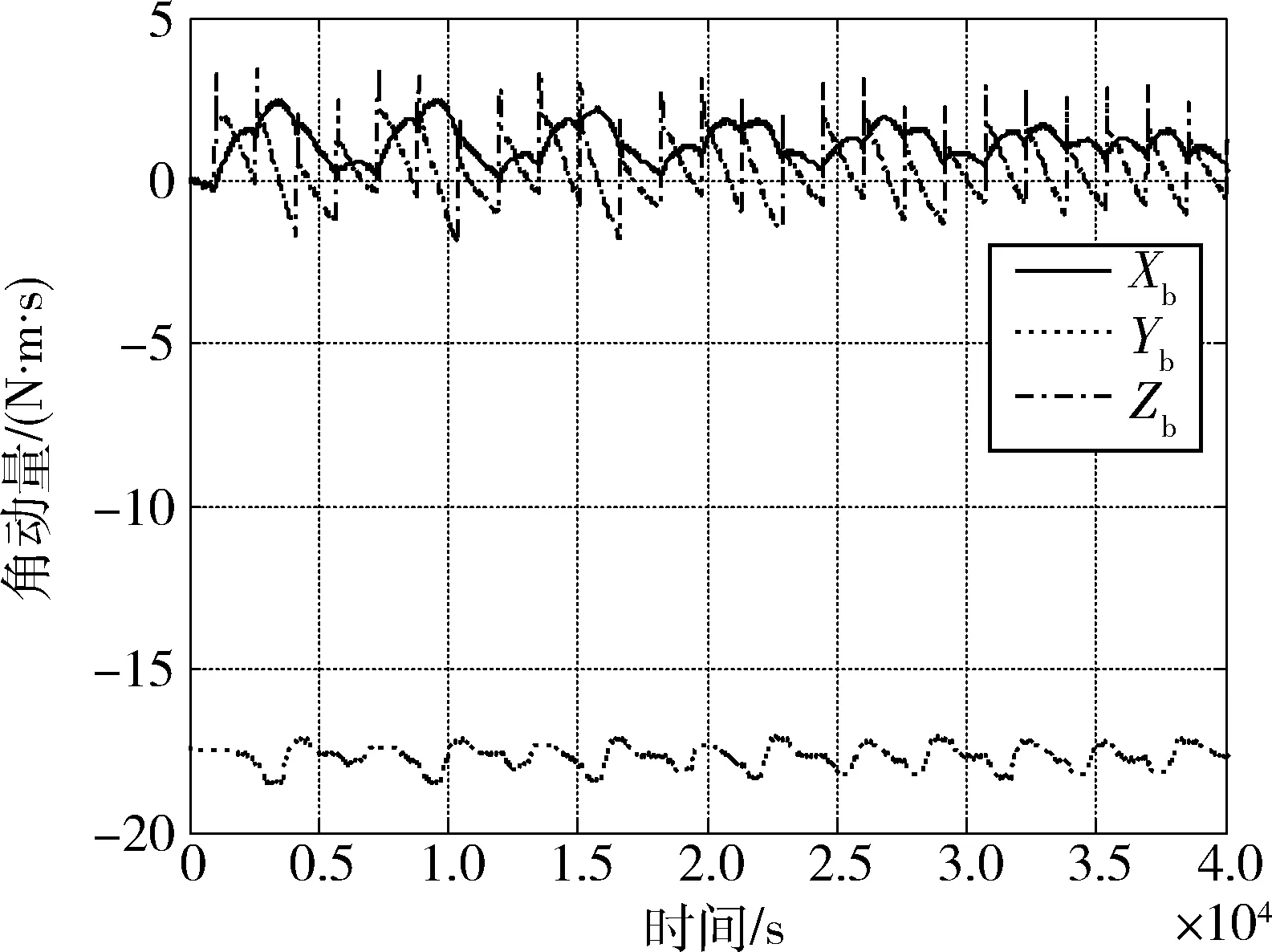
图8 飞轮系统角动量Fig.8 Momentum of flywheel system

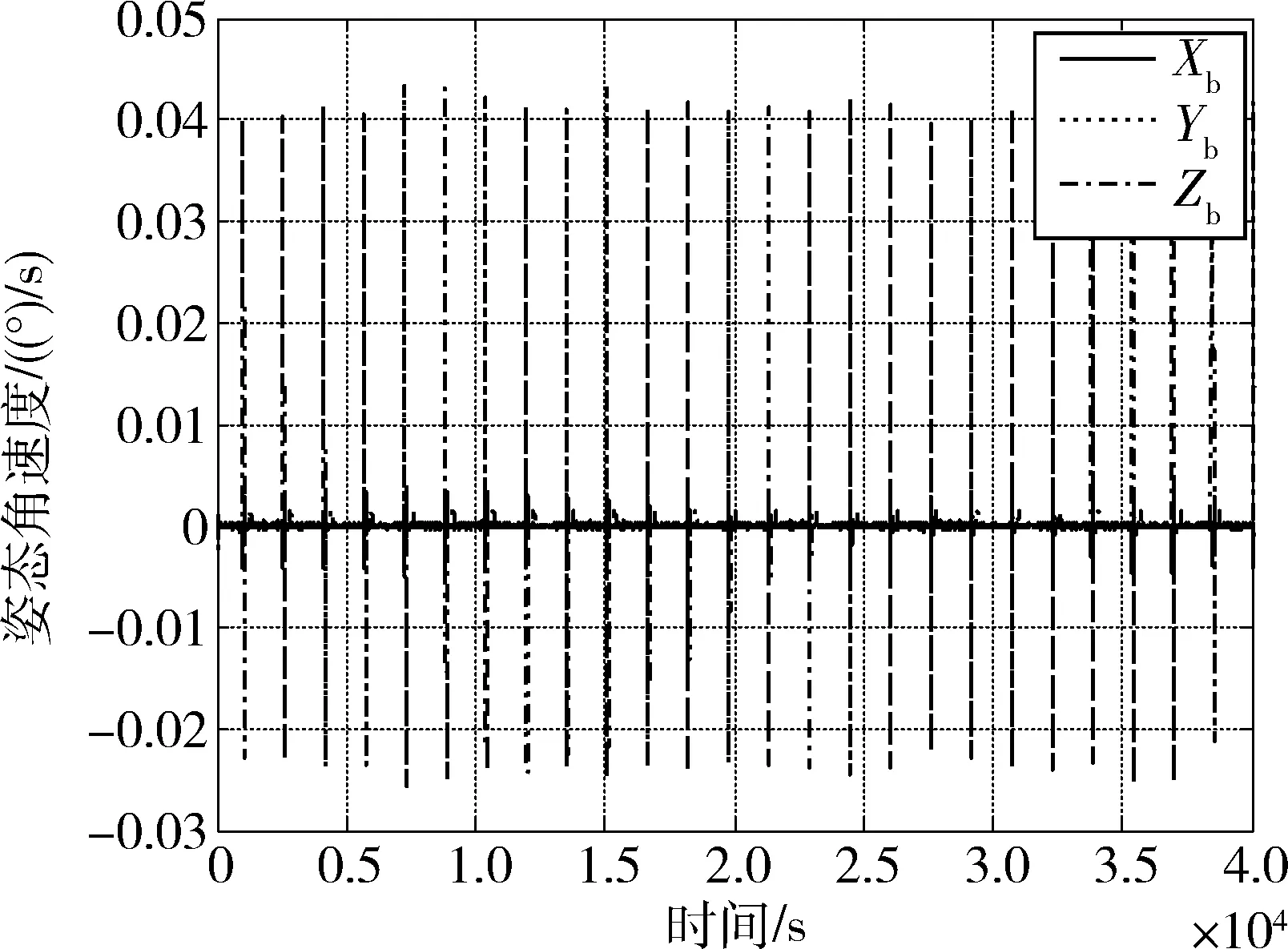
图9 三轴姿态角速度曲线Fig.9 Attitude rates

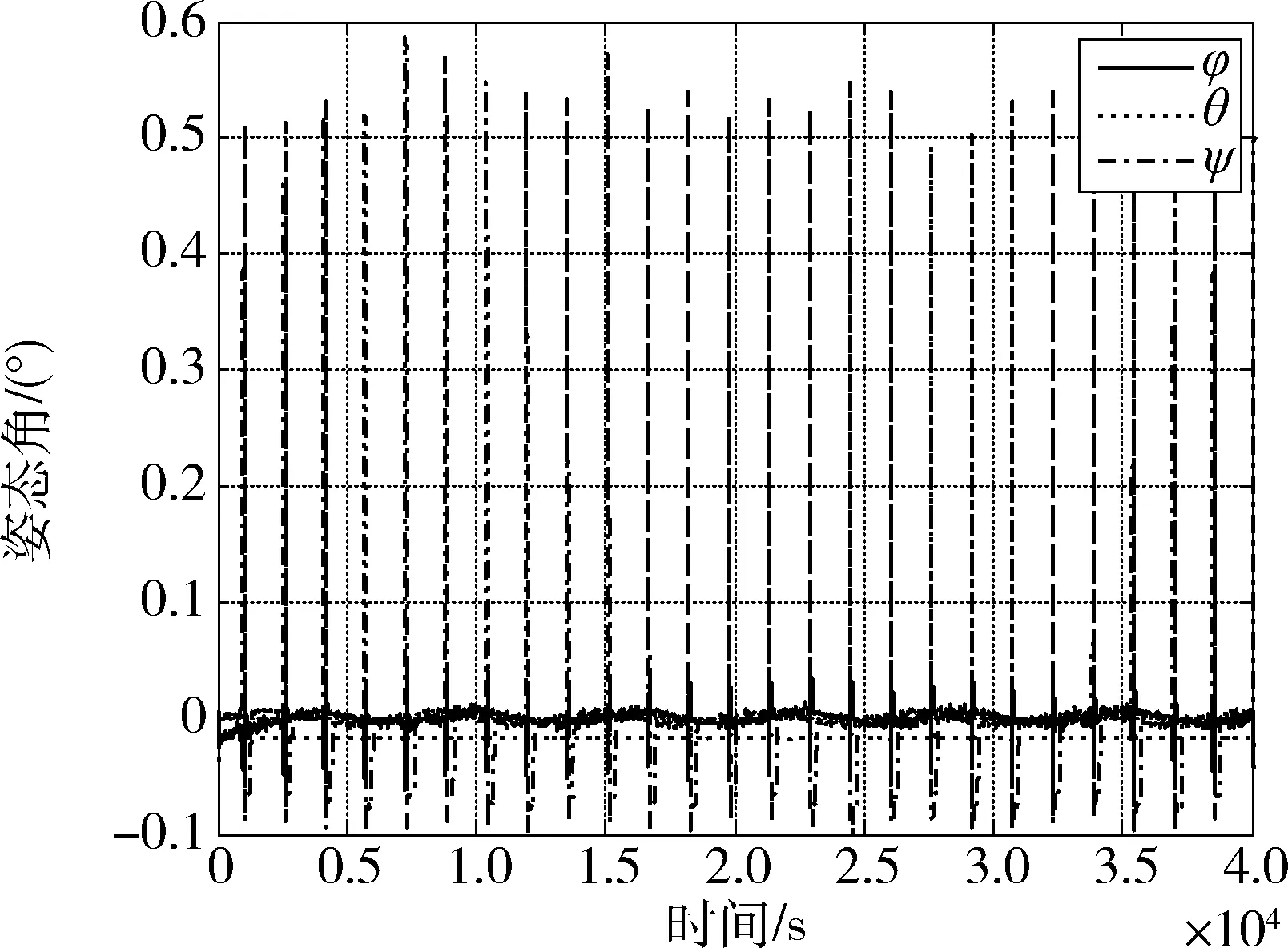
图10 三轴姿态角曲线Fig.10 Attitude angles

通过数学仿真结果可知，在轨控推力器产生的干扰力矩不使飞轮系统饱和的前提下，通过合理设置轨控策略，可实现轨控干扰积累角动量在轨道周期内自平衡相消.

将上述方法应用于在轨航天器，基于1.0 N·m轨控推力器，历时14天自主完成 1578次轨道控制任务，顺利进入目标轨道，为星上有效载荷工作提供了条件.

4 结 论

本文针对利用飞轮系统实现轨控姿态维持的情况，基于对轨控干扰力矩积累角动量变化规律的分析，提出了一种结合偏置角动量建立与对称分布轨控位置选择的轮系角动量管理方法，实现了干扰力矩积累角动量的自平衡相消.基于本文所提出的方法，结合在轨航天器实际对象进行应用研究，应用效果表明该方法可有效地提高轨控效率且避免大干扰力矩下轮系角动量饱和的问题.

参 考 文 献

[1] 陈洁，汤国建. 中低轨道卫星控制方法[J].上海航天，2005(1)：24-30.

CHEN J, TANG G J. The method of medium-low altitude satellite control[J].Aerospace Shanghai, 2005

(1):24-30.

[2] 孙承启. 航天器开普勒轨道和非开普勒轨道的定义、分类及控制[J].空间控制技术与应用, 2009 35(4):1-5.

SUN C Q. Spacecraft Keplerian orbits and non-keplerian orbits: definition, classification and control[J].Aerospace Control and Application, 2009,35(4):1-5.

[3] 唐生勇，张世杰，张育林，等. 姿轨一体化控制航天器推力器构型设计[J].航天控制, 2010,28(3):20-28

TANG S Y, ZHANG S J,ZHANG Y L, et al. Redundant thruster configuration design for the integrated orbit and attitude control of spacecraft[J].Aerospace Control, 2010,28(3):20-28.

[4] 李剑锋, 邓红兵, 赵亮, 等. 基于动量轮转速标定的轨道控制方法研究[J].飞行器测控学报, 2013, 32(6):543-548.

LI J F，DENG H B，ZHAO L, et al. A method of westward longitude maneuver based on calibration of mw revolution speed[J].Journal of Spacecraft TT & C Technology, 2013,32(6):543-548.

[5] 王新民, 张俊玲, 袁军, 等. 欠驱动三轴稳定卫星的消旋和进动控制技术[J].空间控制技术与应用,2014,40(3): 14-18.

WANG X M, ZHANG J L, YUAN J, et al. Despinning and precession control for under-actuated three-axis stabilized satellite[J].Aerospace Control and Application, 2014,40(3):14-18.

[6] 郭朝礼，王淑一，张笃周. 基于偏置角动量的欠驱动航天器姿态保持控制[J].中国空间科学技术, 2014(5)：49-55.

GUO C L, WANG S Y, ZHANG D Z. Underactuated spacecraft attitude hold control based on bias momentum wheel[J].Chinese Space Science and Technology, 2014(5)：49-55.

[7] CHOBOTOV V A. Spacecraft attitude dynamics and control[M].Florida (USA): Malabar Krieger Publishing Company, 1991.

[8] 屠善澄. 卫星姿态动力学与控制[M].北京:科学出版社, 2001.