应用有限元法分析变压器绕组固有振动特性

王丰华 杨毅 何苗忠 杜胜磊 刘石 杨贤

摘 要：为进一步理解和掌握变压器绕组的固有振动特性，建立变压器绕组的三维有限元模型，给出变压器绕组正常与预紧力改变时的固有频率及其对应的振型。同时以某10 kV实体变压器绕组为试验对象，对其模态特性进行了测试分析。计算得到的变压器绕组固有振动特性与测试结果吻合良好，说明所建立的变压器绕组有限元模型的正确性。此外，变压器绕组正常状态时，前四阶固有频率对应的振型呈现不同的振动形态，且对称性较好。绕组预紧力改变时，变压器绕组各阶固有频率均随预紧力增大而增大，但增幅各异，高阶固有频率对预紧力的变化更为敏感。

关键词：变压器；绕组；振动；固有频率；振型

中图分类号：TM 401.1

文献标志码：A

文章编号：1007-449X（2018）04-0051-07

Abstract：To further understand and master the inherent vibration features of transformer winding， the 3-D finite element model of transformer winding is built to calculate the natural frequency and the corresponding vibration pattern. Meanwhile， the model experiment of some real 10kV power transformer was made on the transformer winding. The results of simulation and experiment match well， which verifies the correctness of the simulation model. It is shown that the vibration patterns corresponding vibration patterns were in different shapes and good symmetry when the winding was under normal condition. When the precompression force of transformer winding was changed， the first four-order natural frequencies were increased with the increasing of precompression in different amplitudes.The high order natural frequency was more sensitive to the variations of precompression.

Keywords：power transformer； winding； vibration； inherent frequency； vibration pattern

0 引 言

統计结果表明[1-2]，变压器大多数故障源于出口短路引发的绕组变形或松动。突发短路时，巨大的短路电动力可能会使变压器绕组出现松动或变形等故障隐患，消弱变压器绕组的机械稳定性，此时，即使遭受较小的短路冲击也有可能引发变压器绕组坍塌等大的事故。因此，有必要研究及时有效的变压器绕组状态检测方法，提高变压器及电力系统的安全可靠运行。

近年来，从变压器绕组机械动力学特性出发的振动检测法日益成为国内外的研究热点，鉴于对变压器绕组振动特性进行建模研究可为获取绕组振动规律提供重要的理论依据，研究者从上个世纪70年代初就开始了对变压器绕组的轴向振动特性进行研究。主要分为两大类：基于弹簧-质量系统的变压器轴向振动集中参数模型和有限元分析模型。第一类模型最早由Swihart[3]等提出，即将线饼等效为刚体，将绝缘垫块等效为弹性元件，然后通过该模型得到了绕组在电磁力作用下的位移、加速度等特征。文献[4-5]分析了短路电动力作用下变压器绕组的轴向振动特性，得到了不同预紧力下线饼轴向位移随电流和绕组分接区域的变化规律。文献[6]以电缆变压器为研究对象，计算分析了瞬态短路力激励下的绕组振动规律，讨论了预紧压强、撑条根数等因素对绕组轴向振动的影响。文献[7]定性分析了绕组轴向预紧力与器身轴向固有频率之间的关系。但是，该等效模型无法准确分析绕组几何结构等对其振动的影响，导致计算结果与绕组的实际振动特性存在一定偏差。第二类模型是随着有限元分析法的快速发展而产生的。文献[7-8]通过变压器绕组有限元模型，计算分析了不同预紧力下变压器绕组的一阶固有频率及其对应的振型。文献[9-10]根据换流变绕组的三维有限元模模型，计算分析了变压器在稳态和短路条件下的绕组电磁力特性及其激励下的绕组振动及固有频率。文献[11]计算了变压器绕组在漏磁场作用下的电动力特性，然后将短路电动力作为绕组轴向振动载荷分析了绕组的稳定性，得出了绕组各个线饼的位移分布。但现有研究大都对变压器绕组正常状态下的振动特性进行计算分析，对绕组本身的固有振动特性及其随绕组状态改变的变化规律尚不清楚。尤其是绕组松动时，变压器的电参数如短路电抗、分布电感和分布电容等对其欠敏感，需要寻求其他有效的检测手段，如振动检测法等。

本文尝试建立变压器绕组的三维有限元模型，计算分析变压器绕组正常及松动状态下轴向固有振动特性及其变化规律。同时，对实体变压器绕组为对象进行模态特性测试，用以修正和完善仿真模型，期望获得更为准确的变压器绕组轴向振动特性，为变压器绕组结构优化设计和绕组变形振动检测法提供依据。

1 绕组固有振动特性的有限元建模

1.1 理论分析

变压器绕组是一个典型的复杂多自由度机械系统，而绕组轴向振动是电磁力激励下的强迫振动，满足如下动力学方程，为

式（7）中，等号左侧二项分别为单元刚度矩阵和单元质量矩阵。若将各个单元坐标变换后的单元质量矩阵和单元刚度矩阵组集，便可根据达朗贝尔原理得到如式（2）所示的绕组结构动力学方程。

1.2 变压器绕组的有限元建模

以某10kV变压器高压绕组为研究对象进行有限元建模，该绕组结构为线饼式结构。因主要计算分析变压器绕组的轴向振动特性，故根据变压器绕组结构尺寸在有限元建模时采用如下方法：

1）将绕组等效为一整块环状饼行实体，材质为铜，分别设置了弹性模量、泊松比和密度等参数，由实际测试得到。绕组首末两端各设置一圈刚性挡板，主要参数为弹性模量和泊松比，根据变压器绕组预紧力的设置值和变压器绕组模态测试结果等效及调整得到。

2）绝缘垫块模型根据绕组实际结构尺寸建立，以长方实体结构等效。因其弹性模量随预紧力变化而变化，故将其视为非线性材料。根据垫块的实测应力—应变曲线进行拟合得到其弹性模量变化曲线。

3）线圈、垫块均选用solid 45单元类型；

4）对绕组上下两端实行全约束，主要考虑轴向自由度。

根据变压器绕组实际结构，整个绕组模型共66层线饼，每层线饼间均匀分布了8块垫块。对所建立的变压器绕组有限元模型进行扫掠剖分后，共得到38 448个单元，如图1所示。

2 变压器绕组模态测试描述

实验对象为一台10 kV变压器高压绕组，其实物图片如图2所示，主要对其轴向模态特性进行了测试。

图3为模态测试分析系统图。图中，信号发生器用于产生20 kHz的带宽白噪声信号，经过功率放大器进行放大后，驱动垂直悬挂的激振器对变压器绕组进行激励。其中，激振器端部细杆末端装有力传感器，用于采集激励力的大小。数据系统采集激振器力信号与振动加速度传感器信号，计算出各测点处的频响函数。采用单点激励多点拾振法对变压器绕组进行模态测试，分批次进行。其中，加速度传感器被固定在金属夹件上，沿轴向布置5层，每层4个，共20个测点。

图4为模态实验得到的变压器绕组振动频响函数（vibration frequency response function，VFRF）。為清晰起见，纵坐标采用对数坐标表示。由图可见，振动频响函数的形状随频率变化有着较为明显的峰值，且均在低频部分存在较大的噪声干扰。考虑到，多参考点最小二乘复频域法（polyreference least-square complex frequency domain method， PolyMAX）特别适用于大阻尼和密集模态结构模态参数的识别[12]，故本文在此选用该算法对变压器绕组的模态参数进行识别。

3 结果分析

3.1 绕组正常工况下的固有振动特性

表1分别为计算和根据绕组模态测试结果得到的变压器绕组前四阶固有频率。由表可见，绕组前四阶固有频率的计算结果与试验结果的偏差均在6%以内，说明了计算结果的正确性。出现偏差的主要原因可能是由于实际绕组在端圈及各种夹件固定下使得仿真模型的边界条件与实际情况存在差异。此外，变压器绕组的前四阶固有频率均远离100 Hz的电动力激励频率，不易引发共振。

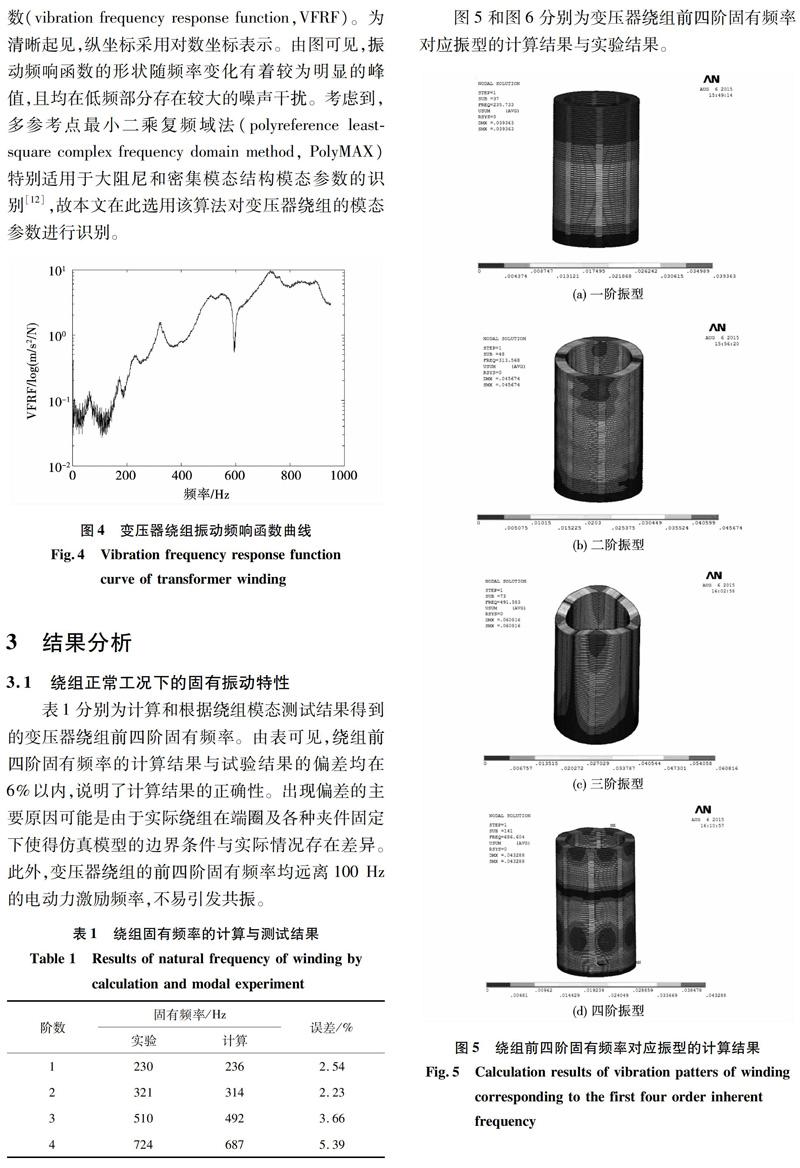
图5和图6分别为变压器绕组前四阶固有频率对应振型的计算结果与实验结果。

图6中，黑色实线部分为静止的绕组位置，红色虚线部分为运动中的绕组位置。由图可见，前四阶固有频率对应振型的仿真结果与实测结果有着较好的一致性，其中，一阶振型均表现为绕组的整体上下振动，二阶振型为绕组的左右“跷板”式振动，三阶振型为绕组两端翘起、中间落下的形态，四阶振型为绕组两端向中间部分挤压的形态。显然，这一结果进一步说明了本文所建立的有限元仿真模型可以较为准确地对变压器绕组的机械特性进行计算分析。

3.2 绕组预紧力变化时的固有振动特性

考虑到绕组松动（预紧力下降）是在运变压器的常见故障之一，且如何寻找合理的变压器绕组预紧力范围一直是变压器制造厂关心的焦点之一，本文在此根据所建立的有限元仿真模型，重点分析了绕组预紧力变化时的固有振动特性。

已有的研究表明，绕组线饼间的绝缘垫块是一种刚度渐硬材料，其刚度系数随绕组预紧力的大小有较明确的变化。由文献[8]知，变压器绕组绝缘垫块的弹性模量E可表示为

显然，垫块的弹性模量随压强的增大而增大。故可通过改变有限元仿真模型中垫块材料弹性模量模拟预紧力改变时的绕组固有振动特性。

图7为变压器绕组前四阶固有频率随预紧力改变的变化曲线。图中，FN为变压器绕组预紧力设计值。由图可见，当变压器绕组预紧力降低即绕组松动时，绕组前四阶固有频率向低频方向偏移；预紧力增大时，绕组前四阶固有频率向高频方向偏移。其中，绕组预紧力在80%FN～120%FN变化时，绕组前三阶固有频率的变化率约为20%；绕组预紧力在40%FN～80%FN变化时，绕组前三阶固有频率的变化率约为30%。此外，绕组第四阶固有频率较前三阶固有频率的变化更加明显。因此，当有松动隐患的变压器绕组遭受频率分量较为丰富的激励力作用，例如突发短路的情形，若激励力的频率分量与绕组的固有频率较为接近时，有可能会引发变压器绕组共振而引起绕组坍塌，导致变压器故障。同时，对变压器制造厂来说，若已知变压器绕组预紧力设计值时对应的固有频率，则可从绕组固有频率的变化程度对绕组的压紧程度进行预估，从而指导变压器生产实际。

限于论文篇幅，本文在此给出了变压器绕组预紧力为80%FN时其前四阶固有频率对应的振型，如图8所示。

此时，绕组的前四阶固有频率分别为225 Hz、301 Hz、480 Hz和658 Hz。由图8可见，绕组松动时，一阶振型均表现为绕组的整体上下振动，二阶振型为绕组的左右“跷板”式振动，三阶振型为绕组两端翘起、中间落下的形态，四阶振型为绕组两端向中间部分挤压的形态，与绕组正常状态的振型形态类似，并具有较好的对称性。但是，绕组固有频率的变化会使得变压器绕组在类似激励力下的固有振动特性发生改变。相应地，绕组振动信号也会随之发生改变。

4 结 论

1）变压器绕组正常状态下前四阶固有频率和对应的振型与繞组激振实验结果吻合良好，说明了所建立的有限元模型的正确性。应用该模型，可以方便地对变压器绕组的固有振动特性进行分析。

2）变压器绕组正常状态下的前四阶固有频率所对应的振型对称性较好。绕组松动时，前四阶固有频率均随预紧力的降低而降低，但变化幅度存在差异。预紧力增大时，前四阶固有频率也随之增大。

3）绕组预紧力改变时引发的绕组固有振动特性的改变必然会使得绕组振动信号发生改变，尤其需要关注突发短路时有松动隐患的变压器因固有频率向低频偏移而引发的共振问题。

本文所用仿真和模态测试手段同样可推及更高电压等级的变压器绕组，考虑到变压器绕组故障的多样性和复杂性，对不同故障类型及故障程度下的变压器绕组固有振动特性进行计算分析是我们下一步的研究方向。

参 考 文 献：

[1] 顾晓安，沈荣滋，徐基泰. 国外变压器噪声研究的动向[J]. 变压器，2002，39（6）：33.

GU Xiaoan， SHEN Baozi， XU Jitai.Trend of transformer noise research abroad [J]. Transformer， 2002， 39（6）： 33.

[2] WANG F H， JIN Z J. Using the vibration frequency response analysis method to detect the winding deformation of power transformer[C]//IEEE PES General Meeting， Detroit， U. S. A， July 2011.

[3] SWIHART D O， WRIGHT D V. Dynamic stiffness and damping of transformer pressboard during axial short circuit vibration [J]. IEEE Transactions on Power Apparatus and Systems， 1976， 95（2）： 721.

[4] 王洪方，王乃庆，李同生.变压器绕组轴向预紧力对绕组轴向振动特性的影响[J].电网技术，1999，23（9）：8.

WANG Hongfang， WANG Naiqing， LI Tongsheng. Influence of axial pre-compression level on axial vibrations in transformer windings[J]. Power System Technology， 1999， 23（9）： 8.

[5] 王洪方，王乃庆，李同生.大型电力变压器绕组轴向非线性振动研究[J].电网技术，2000，24（3）：42.

WANG Hongfang， WANG Naiqing， LI Tongsheng.Axial nonlinear vibration of large power transformer winding[J]. Power System Technology， 2000， 24（3）： 42.

[6] 王世山，汲胜昌，李彦明.电缆绕组变压器短路时线圈轴向稳定性的研究[J].中国电机工程学报，2004， 24（2）： 166.

WANG Shishan， JI Shengchang， LI Yanming. Study on axial stability in condition of short-circuit for power transformer using XLPE insulated cable windings [J]. Proceedings of the CSEE， 2004， 24（2）： 166.

[7] 李岩，周伟，井永腾，等.短路条件下变压器器身轴向振动的分析[J]，电工电能新技术，2012，31（3）：49.

LI Yan， ZHOU Wei， JING Yongteng， et al. Axial vibration analysis of transformer active part under short-circuit [J]. Advanced Technology of Electrical Engineering and Energy， 2012， 31（3）： 49.

[8] 李洪奎，李岩.不同预紧力下变压器绕组轴向振动模态分析[J].电机与控制学报，2010，14（8）：98.

LI Hongkui， LI Yan. Axial vibration modal analysis of transformer windings under different level of pre-compression [J]. Electric Machines and Control， 2010， 14（8）： 98.

[9] 许加柱，罗隆福，李勇，等.新型换流变压器绕组电磁力的分析计算[J]，高电压技术，2007，33（6）：102.

XU Jiazhu， LUO Longfu， LI Yong， et al. Analysis and calculation of windings electromagnetic force of a novel converter transformer[J]. High Voltage Engineering， 2007， 33（6）： 102.

[10] SHAO Pengfei， LUO Longfu， LI Yong， et al.Electromagnetic vibration analysis of the winding of a new HVDC converter transformer[J]. IEEE Transactions on Power Delivery， 2012， 27（1）： 123.

[11] 郭健，林鹤云，徐子宏，等.用有限元方法分析电力变压器绕组轴向稳定性[J]，高电压技术，2007，33（11）：209.

GUO Jian， LIN Heyun， XU Zihong， et al. Analysis of axial stability of power transformer windings using finite element [J]. High Voltage Engineering， 2007， 33（11）： 209.

[12] 孙鑫晖，郝木明，王淮维. PolyMAX模态参数识别算法的快速实现[J]. 振动与冲击，2011，30（10）：5.

SUN Xinhui， HAO Muming， WANG Huaiwei. Fast implementation for PolyMAX modal identification algorithm[J]. Journal of Vibration and Shock， 2011， 30（10）： 5.

（编辑：刘素菊）