供热系统均衡工况研究★

孔 婵 徐子龙 赵昕波 程鹏月 刘 锦 任佳艺 赵 琦

(河北建筑工程学院，河北 张家口 075000)

集中供热系统由热源、热网和用户三部分组成。在供热系统中，通常按照供暖热负荷随室外温度的变化规律，作为供热调节的依据[1]。在供热系统热源随负荷变化的过程中，最关键的是对热网水力工况的调整。热网水力工况的优化调度，可以使得管网充分发挥其输配能力，为热源的合理匹配与调整创造最大的空间；另外，输配系统本身的动力消耗也是巨大的，一般要占到整个供热系统一次能源消耗10%～20%，而水力工况的优化调度可以尽可能地减少这部分的能量消耗[2]。而如何找到在既定系统使每个用户都能达到最优状态的最优分配及均衡工况是本文的重点。

1 工况定义

供热系统的热力工况指的是供热量、温度等参数的分布状况。在热力工况的研究中，对用户室内温度分布状况的分析尤为重要，供热效果的好坏与室内实际温度是否达到设计温度有着直接关系。因此，不管是供热系统设计还是供热系统运行，分析研究供热系统的热力情况始终是最重要的任务。供热系统压力、流量等参数的分布状况称为水力工况。由于供热系统的供热量是通过热媒进行输送，热媒的输送情况直接影响供热量的分布状况，进而影响室内温度的分布状况。而热媒的输送状况通常是通过其压力、流量等来描述，因此，水力工况是热力工况的源头，研究热力工况，必须着手研究水力工况[3]。

2 运行调节

用户室温与多种因素有关，如室外温度、管网流量、采暖供水温度、建筑物耗热量等。因此，除了在供热系统运行之前进行初调节外，还应在系统运行期间根据室外温度的变化对热网的供水温度、流量等进行调节，以使用户室温达到要求，这种调节方式称作供热系统的运行调节。本文在整个供暖期，采用量调节，由于循环水量随室外温度而变化，故运行电耗大大减少，并通过自动控制调节循环水泵的流量，解决其操作复杂的缺点[4]。

3 均衡工况

3.1 最优分配

以流量和压力为水力工况参数，以供热量和供水温度为热力工况参数。

首先观察一个简单的供热系统，不考虑热源，通过流量调节使两者的流量进行再分配，但是用户都是自利的，则这种自利行为是对流量再分配的唯一途径。假设在这个供热系统内只有两个用户，分别为用户1和用户2；考虑两个参数，流量m和供回水温差ΔT。设供热量为Q，则有：

Q=cmΔt。

其中,Q为供热量，kJ；c为水的比热容，kJ/(kg·℃)；m为水的质量，kg；Δt为供回水温差，℃。

令e1=(m1，ΔT1)和e2=(m2，ΔT2)分别表示用户1和用户2所得到的热量禀赋。在设计室外温度下，各个用户室内温度达到tn，整个供热系统的需热量是Q，设计总流量是m，供回水温差为Δt，则有Q=cmΔt。

这种供热系统可用埃奇沃思盒状图来分析[5]。图1中，横轴表示流量m，纵轴表示供回水温差ΔT。用户1和用户2分别以左下方和右上方为起始点。从O1点出发沿着底边向右移动，表示用户1的流量m1增加；从O2点出发沿着顶边向左移动，表示用户2的流量m2增加；同理，从O1点出发在左侧垂直向上移动，表示用户1的供回水温差ΔT增加；从O2点出发往右侧垂直向下移动，表示用户2的供回水温差ΔT增加。如此构造出的盒状图，其宽度度量流量的总量m，其高度度量供回水温差ΔT的最大值(下标表示消费者)。

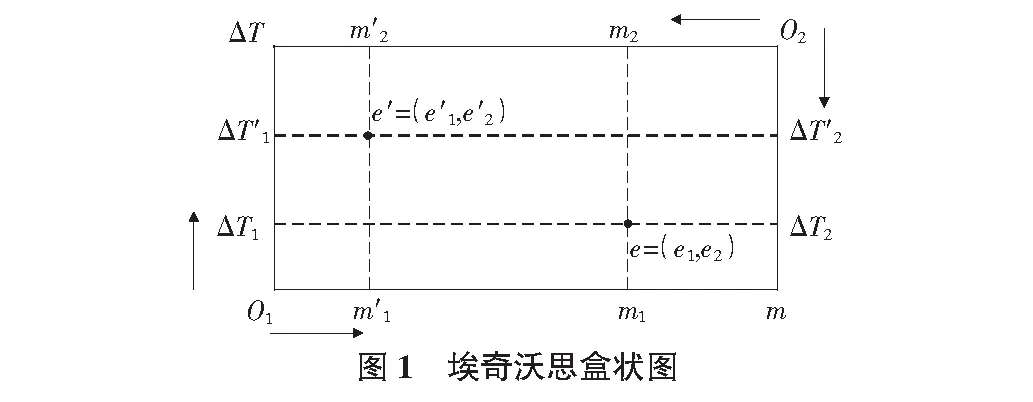
盒状图中的每个点都有四个坐标——其中两个表示用户1所得到的流量和供回水温差，另外两个表示用户2所得到的流量和供回水温差。盒状图的宽与高分别由总流量和总供回水温差所固定。

假设每个用户的舒适偏好都可以用正常的、凸的无差异曲线图来表示。

在图2中，用户1的无差异曲线图谱沿着右上方增加，用户2则沿左下方增加。对每个用户来说，盒中的每个点都只能有一条无差异曲线经过。标有LL的曲线是两个用户无差异曲线切点的连线，它是分配方案的子集，称为契约线，见图3。

契约线说明用户如何通过分配实现最大的满足程度，即分配的最优境界。在这种分配状态下，任何再分配都不可能使一个用户的满足水平提高而不使另一个用户的满足水平下降。

在图2中，假定在某一室外温度tw下，用户1和用户2的需热量分别为Q1和Q2，此处无差异曲线1和2分别代表用户1和用户2的需热量Q1,Q2，而用户1的供热情况处于a点，用户2的供热情况处于b点。在这个供热系统中，显然最优分配的第一个条件就是最优分配一定“在盒状图中”，因为只有盒状图中的配置方案是可行的，但并非每种可行配置都是最优分配。

情况一：室外温度下降至tw1，假定室外温度tw1下的系统总供热量为Q′，系统总流量为m′，总供回水温差为Δt′。则用户1的需热量增至Q1′，循环流量为m1′，供回水温差为Δt1′；用户2的需热量增至Q2′，循环流量为m2′，供回水温差为Δt2′。现有曲线3代表需热量Q1′的无差异曲线，曲线4代表需热量Q2′的无差异曲线，则用户1需从a点调节至无差异曲线3上的某点c，用户2需从b点调节至无差异曲线4上的某点d，且满足Q′=Q1′+Q2′，m′=m1′+m2′。则有式(1)成立：

m′Δt′=m1′Δt1′+m2′Δt2′

(1)

无差异曲线3上的某点c若再分配至无差异曲线3的右侧某一点，则从式(1)中可以看出，d点将会被再分配至无差异曲线4的右侧某一点，此时，虽然用户1的供热量增加，但用户2的供热量减少，不满足供热要求，因此，此分配会被用户2抵制。同样地，若d点再分配至无差异曲线4的左侧某一点，则此种再分配会被用户1抵制。

现在来看一下，是不是无差异曲线3上的每一点及无差异曲线4上的相应点都是用户1和用户2的最优分配。

首先通过前面论述，可知无差异曲线3与契约线的交点一定是最优分配点，其次考虑无差异曲线上但未在契约线上的点。当用户处于这些点时，流量与供回水温差通过无数组合仍能使用户1与契约线上的点c′达到相同的供热效果，对应的，在无差异曲线4上的点也能使用户2达到与契约线上的点d′一样的供热效果。且用户1从c点再分配至c′点并不会使用户2的供热效果变得更好，对应的，用户2从d点再分配至d′点也并不会使用户1的供热状况变得更好，因此，无差异曲线3上的每一点与对应的无差异曲线4上的点使供热系统处于最优分配状态。因本文采用量调节，故最优分配应是在上述最优分配的基础上，给定供热系统的供水温度，通过流量与供回水温差的组合，仍能使用户获得所需的供热量。所以这点是供水温度线与无差异曲线的交点。

情况二：室外温度上升至tw2，此时曲线5代表需热量Q1″的无差异曲线，曲线6代表需热量Q2″的无差异曲线，则用户1需从a点调节至曲线5上的某点e，用户2需从b点调节至曲线6上的某点f。

与情况一类似，我们可以直接得出：无差异曲线5上的每一点及无差异曲线6上的相应点都是用户1和用户2的最优分配，且最优分配点既在用户所需供热量的无差异曲线上，又在供水温度线上。

接下来我们推广到n个用户的情况。令N={1,2，…，n}表示用户集合。如果一种分配在不使其他用户的状况严格变坏的情况下就无法使某些用户的状况严格变好，则这种分配是有效的。如果X是有效分配，则供热系统不能偏离X，因为一旦偏离X达到其他可行分配，则要想改善任一用户的状况必定会使至少一个用户的状况受损。因此，这种再分配会被至少一个用户抵制。

综上所述，供热系统一旦达到最优分配，则在不会使其他用户的情况变坏的前提条件下，供热系统的分配调整也不再可能使任何热用户的情况变得更好，即不可能移至盒状图中的其他位置。这种分配就是最有效率的，满足这样的分配就是最优分配。

3.2 均衡工况

在分析最优分配时我们引入一个盒状图，其横纵坐标分别是流量和供回水温差。对应于最优分配的工况点就是最佳工况。此处我们采用量调节，且各用户的供水温度相等。在此我们能够得到供水温度一定时流量的分配情况。当用户需热量变化时，各用户的循环流量也要随着变化，因为处于最优分配，所以在供热系统运行调节过程中的各用户的流量就是均衡工况。

参考文献:

[1] 贺 平,孙 刚.供热工程[M].北京:中国建筑工业出版社,2009:277.

[2] 秦绪忠,江 亿.多热源并网供热的水力优化调度研究[J].暖通空调,2001,31(1):11-16.

[3] 石兆玉.石兆玉教授培训技术报告[DB/OL].https://max.book118.com/html/2016/0812/51167139.shtm,2016-08-12.

[4] 李善化,康 惠.集中供热设计手册[M].北京:中国电力出版社,1995:321-328.

[5] Geoffrey A.Jehle,Philip J.Reny.Advanced Microeconomic Theory(Third Edition)[M].Beijing:The Chinese People’s University Press,2015:151-154.