考虑损伤时变特性的大跨斜拉桥抗震性能研究

郑宇倩，王 莹

（东南大学 江苏省工程力学分析重点实验室，南京 210096）

大跨斜拉桥作为交通运输的枢纽工程，一旦在地震中遭遇破坏，势必造成巨大的经济损失，给抗震救灾及灾后重建带来巨大影响，因此，对其抗震性能的研究具有重要的现实意义。

大跨斜拉桥服役期间，车辆交变荷载和环境变温[1]等日常服役荷载的耦合作用以及台风、地震等突发性荷载作用会引起结构发生损伤，随着服役时间增长，损伤不断累积，严重削弱其承载能力，造成其使用功能的衰退，尤其对地震荷载而言，其具有强度大、随机性强、时间短的显著特征。公路桥梁抗震设计细则（JTG/TB02-01—2008）[2]明确要求抗震设防烈度6度及以上地区的公路桥梁，必须进行抗震设计。常规的抗震设计只针对设计时的完好结构，尚未考虑服役期间的损伤累积所导致的性能劣化，而材料的性能劣化将不可避免地影响到结构不同服役期的抗震性能，使得面向完好结构的抗震性能设计与服役期内实际结构真实的性能存在一定的偏差，这样的偏差对于设计精度较高的桥梁结构的影响是不可忽视的。

对于突发性的地震载荷，许多学者致力于地震损伤模型建立和损伤指标量化的研究。王振宇[3]和沈祖炎[4]等基于各类地震损伤模型，从材料、构件和结构等3个层次对国内外结构地震损伤评估的研究成果进行了系统总结和综合评述；陆本燕等[5]以钢筋混凝土桥墩为研究对象，对8个典型的地震损伤模型进行了对比分析，结果表明Park&Ang模型与试验符合较好，刘伯权模型考虑了低周疲劳效应，其概念简单、应用方便；孙颖等[6]以墩顶漂移率作为设计参数，通过对大量试验数据的统计分析，给出了与各级不同性能水准相对应的抗震性能指标，供基于性能的抗震设计采用；Kim T H等[7]利用非线性有限单元对钢筋混凝土桥墩地震损伤进行了评估。上述的研究工作均面向设计时初始材料的力学性能以及初始构件和结构的形态，并未考虑到结构在整个服役过程中疲劳损伤的累积所导致的性能劣化对结构地震抗力的影响。

本文针对上述理论研究的不足，以润扬长江大桥北汊斜拉桥为研究对象，对结构的疲劳损伤时变特性进行研究，基于动力弹塑性时程分析法获得了结构在不同服役年限时遭遇地震的响应，并根据桥梁结构性能对照标准和地震损伤模型，研究了该桥的地震时变损伤特性，评估了结构的抗震性能。

1 大跨钢桥地震损伤时变特性研究

本文采用的考虑损伤时变特性的大跨钢桥抗震性能分析的技术路线如图1所示。首先，将桥梁上的车辆交变荷载和环境变温荷载以等效的方式施加于结构的精细有限元模型，得到疲劳关键部位的应力时程曲线，基于雨流计数法和非线性连续介质损伤力学（Continuum Damage Mechanics-CDM）模型，得到结构的累积疲劳损伤值。然后，考虑材料力学性能的时变性对疲劳损伤累积的影响，通过修正材料的力学参数来反映其对结构累积损伤的影响。最后，在不同服役期的结构时变模型上，施加选取的典型地震波，运用动力弹塑性时程分析法获得多遇和罕遇地震下的结构响应；基于地震损伤模型，获得服役期内地震损伤时变规律，根据结构损伤值与抗震设防要求的对应关系，对比了时变特性和时不变结构的损伤值，分析时变特性产生的原因，评估材料损伤时变特性对于结构抗震性能设计准确性的影响。

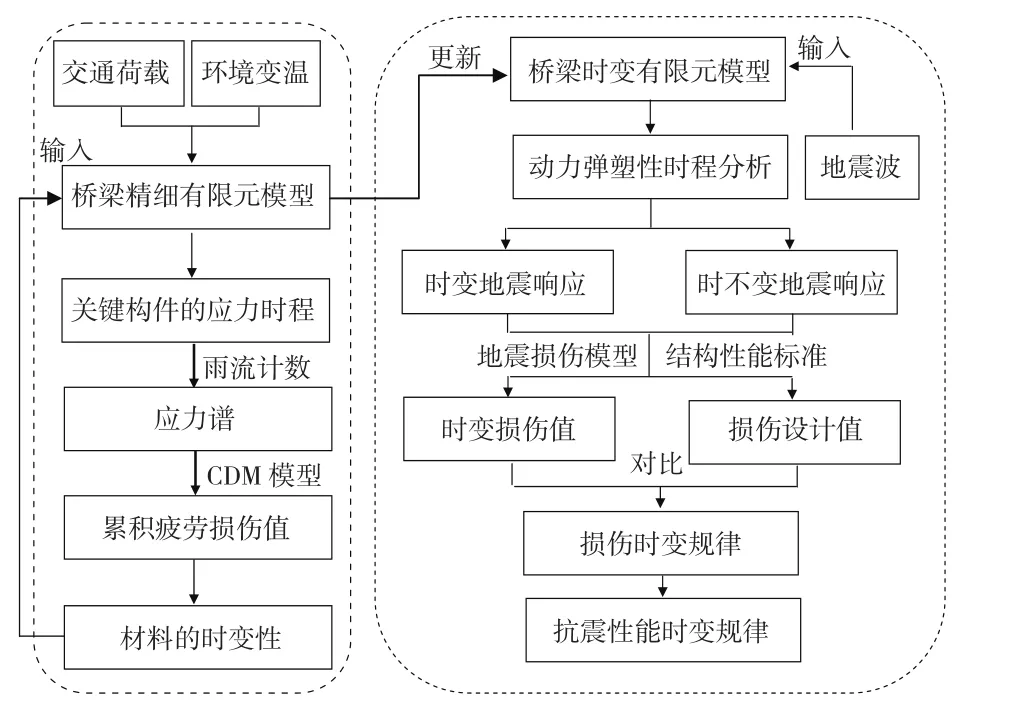
图1 考虑损伤时变特性的大跨钢桥抗震分析的技术路线

1.1 大跨钢桥的疲劳损伤分析

日常运营环境下，大跨钢桥的疲劳损伤主要由车辆载荷和环境变温共同引起，两者均具有较强的随机性。车辆载荷的获得方法有两种：一是在交通流状态调查统计的基础上，利用基于疲劳损伤等效原理的标准疲劳车模型；二是基于Monte-Carlo随机模拟交通载荷谱[1]。而环境变温引起的应力时程，通常借助于热力学参数已知条件下的有限元数值模拟。将上述的两种荷载施加于结构的精细有限元模型，然后通过雨流计数并依据CDM累积损伤模型，即可获得结构在服役期间的累积疲劳损伤值[1]。

1.2 CDM累积损伤模型

传统的桥梁疲劳损伤分析是基于S-N曲线和Palmgren-Miner线性累积损伤准则进行的，这种方法因为形式简单便于理解，被广泛地应用于工程实践中，但是线性的损伤累积准则往往不能准确展现真实的损伤累积过程。所以在近20年里，国内外的学者致力于连续介质损伤力学的研究，为疲劳损伤分析提供了新的研究思路和分析方法，其中连续介质损伤力学（Continuum Damage Mechanics -CDM）模型[8-9]是适合于大跨钢桥构件疲劳损伤累积计算的疲劳损伤模型。

CDM模型为高周疲劳损伤模型，该模型认为在役桥梁结构局部的疲劳损伤是一个非线性的累积过程，桥梁结构在复杂的随机载荷作用下单轴应力状态下高周疲劳损伤演化方程为：

式中：α、β、B为材料常数；符号<σ>为McCauley括号算子；σf为疲劳应力门槛值；σ、和σ*分别为应力幅、平均应力和有效应力。

对于海量的桥梁结构应力时程数据，可建立代表绝大部分应力时程的“标准循环块”，通过对其中应力时程的积分并不断重复“标准循环块”来模拟桥梁实际发生的应力循环所引起的疲劳损伤累积。对标准循环块引起的累积疲劳损伤率进行不断积分，可得到“标准循环块”反复作用下结构的疲劳损伤累积值，如式（2）所示。

式中：mrb为标准块中应力幅值大于疲劳应力门槛值的应力循环数；Nbi为标准应力循环块的数目；Δσi为应力幅值；σmi为平均应力；D为损伤值。

1.3 考虑损伤累积的钢桥时变特性

国内外学者虽然对桥梁构件的损伤机理及累积过程做了深入分析和研究，但无论从结构还是构件角度，对其力学性能及其时变性的研究尚未建立起合理的分析模型。

经典CDM认为弹性模量E是用来表征结构内部损伤累积的力学性能参数，其时变性会直接导致地震响应的时变性，不可避免对结构抗震能力产生影响。为此，本文引入Lemaitre[10]应变等价原理来考察服役过程中桥梁力学性能的时变特征。这一原理认为：应力σ作用在损伤构件上引起的应变与有效应力σt作用于无损构件引起的应变等价。根据这一原理，受损材料的本构关系可通过无损材料的名义应力得到，即：

式中：E为材料在初始状态下的弹性模量，为未损伤时的模量；Et为t时刻受损材料的实际弹性模量，称为有效弹性模量；D（t）为服役t时刻材料的损伤。通过修正服役过程中材料的弹性模量来反映损伤导致的力学性能的劣化。

1.4 地震损伤模型

桥墩位移角不仅是桥梁地震变形中的重要控制参数，也是基于首次被超越准则的地震损伤模型的重要指标，可用来描述斜拉桥在地震作用下的损伤状态。

较多的学者对桥梁结构中最易遭受地震破坏的桥墩的损伤状态进行评估，并根据桥梁的破坏特点和抗震性能设计的需要，将桥梁抗震性能水平划分为完好无损、轻微破坏、中等破坏、严重破坏及倒塌5个性能水平。基于上述性能水准的划分，本文采用的斜拉桥损伤状态的描述如表1所示[6]。

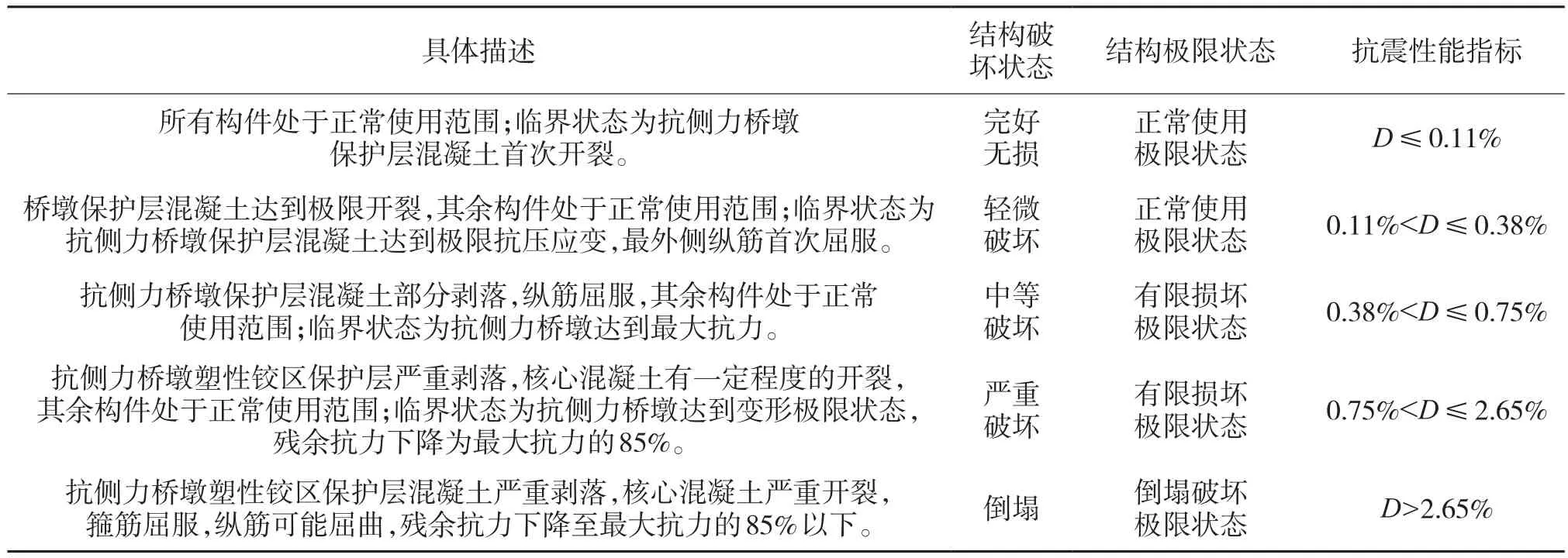
表1 桥梁结构性能水准的划分

对于上述5个等级的损伤表述，不少学者提出了与上述定性的损伤描述所对应的定量的损伤值范围。采用孙颖[6]提出的以墩顶漂移率作为设计参数的地震损伤评估模型作为本文的损伤状态评估模型，如式（4）所示。

式中：Δ为桥梁墩顶响应最大地震反应位移；H为墩柱墩高；D为墩顶漂移率，作为桥梁的地震损伤值。

此模型能够与结构损伤等级和地震设防水准直接联系，能直观评价结构的抗震性能是否达到相应的设防标准。

2 润扬斜拉桥的疲劳损伤时变规律

2.1 工程概况

润扬斜拉桥是连接镇江、扬州的润扬长江公路大桥的重要组成部分，为175.4 m+406 m+175.4 m的三跨连续箱梁桥。主梁采用全焊扁平流线型封闭钢箱梁，其上翼缘为正交异性板结构，采用Q345D钢材，钢箱梁高3 m（中心线处），宽37.4 m。桥面总宽35.4 m，按双向六车道布置。索塔采用空间索面花瓶型混凝土塔柱，桥面以上呈倒Y型，下塔柱呈V型，高约145 m，塔柱采用箱型断面，采用C50混凝土，桥塔长细比很大，是典型的高耸结构。结构设计基准期为100年，抗震设防类别为A，抗震设防烈度为7度。

根据设计图纸建立具有良好准确性和可靠性的三维有限元模型，如图2所示。此模型经过简化并参数修正，动力特性与实测值吻合较好[11]，为本文的地震损伤分析提供了准确的前提条件。

图2 润扬斜拉桥有限元模型

2.2 润扬斜拉桥疲劳损伤的累积规律

在交通状态调查统计的基础上利用基于疲劳损伤等效原理的标准疲劳车模型作为车辆荷载，并基于桥梁健康监测系统的温度传感器所测得的温度模拟环境变温，施加于上述有限元模型，可获得两种荷载共同作用时钢箱梁结构的动力响应。针对桥面板跨中疲劳关键位置，基于CDM的高周疲劳损伤模型考察了两种荷载共同作用下的结构疲劳损伤累积规律，最终获得润扬斜拉桥的累积疲劳损伤如图3所示。

图3 润扬斜拉桥疲劳损伤累积

对上述累积疲劳损伤值进行5阶GAUSS拟合，得到的拟合函数如式（5）。

问卷调查尽量以随机抽样为主，所以调查时采用简单随机抽样来计算大学生群体的样本量，其计算公式为，其中：为总体总量；为一定置信水平下对应的标准正态临界值；为抽样概率；为抽样极限误差.

修改结构的弹性模量，来反映结构在某服役时刻的损伤程度。根据式（3）和式（5）得到材料的有效弹性模量为：

式中：E（t）为某时刻材料损伤模量，称为有效弹性模量；E为材料在初始状态下的弹性模量；D（t）为服役t时刻材料的损伤。

由式（6）可得到的斜拉桥材料损伤时变规律，如图4所示。

图4 润扬斜拉桥材料损伤时变规律

表2提供了润扬斜拉桥服役150年内，每隔10年的材料弹性模量的值。通过选取服役期150年内每隔10年的时变参数值输入润扬斜拉桥有限元模型，控制地震波的输入，采用动力弹塑性时程分析法计算结构的时变响应，即可获得不同服役期的地震损伤值。

3 多遇地震作用下润扬斜拉桥地震损伤时变性能分析

多遇地震作用下，地震动的强度不大，结构的主要承载部分处于弹性变形阶段，一般不会发生较为严重的灾难事故，“小震不坏”是桥梁结构在多遇地震下的抗震设防目标。

表2 润扬斜拉桥模型材料损伤弹模时变特性

根据抗震规范选取加速度时程峰值，选取EI Centro Site地震波、Taft Lincoln School地震波和San Fernando地震波作为本文地震分析的地震波。调整根据所选地震波的加速度峰值，研究结构遭遇多遇地震时的损伤和抗震性能的时变效应。根据前文中的材料在不同年限下的弹性模量的时变规律，选取服役150年内每隔10年的弹性模量值输入精细的有限元模型，控制地震波的输入，实现多遇地震的模拟，得到考虑材料时变特性的结构动力响应。根据相应的地震损伤模型求得结构时变损伤值，并与设计条件下结构的损伤设计值进行对比。

采用动力弹塑性时程分析法所获得地震作用下的润扬斜拉桥各桥墩的最大位移值。从结果看出，无论是横桥向还是顺桥向，各桥墩顶部的水平位移值的差异很小，差值均在1 mm以下，可认为任意桥墩的位移值均可作为结构时变损伤值的动力响应指标。将不同年限的桥墩位移值入式（4），计算结构的时变损伤值并判定结构的性能状态，将其与不考虑时变效应的设计值比较，判别是否满足相应的设防要求。

图5 7级El-Centro地震波下桥墩位移时程图

通过施加不同方向地震波，利用时程分析法可以得到桥墩顶部顺桥向和横桥向最大水平位移，本文取横桥向和顺桥向的位移值系数0.8和0.6将横桥向和顺桥向最大位移进行组合，得到桥墩顶部总的最大位移值，并将每10年的最大位移值输入式（4）中得到地震时变损伤值。图6给出了润扬斜拉桥在各服役期内突遭7级的EI Centro Site地震波、Taft Lincoln School地震波和San Fernando地震波，采用上述的桥梁地震损伤模型得到的地震时变损伤值。

从图6中可以发现，润扬斜拉桥的地震损伤值总体上随服役期的增长而逐渐增加，即桥梁的抗震性能随着桥梁疲劳损伤累积而不断劣化。7级的EI Centro Site地震波作用下的结构地震损伤值明显大于同级的Taft Lincoln School地震波和San Fernando地震波的，主要原因可能是由于前者接近地震时程加速度峰值的时间点多于后者。

图6（a）是7级EI Centro Site地震波作用下的润扬斜拉桥地震损伤时变值。可以看出，损伤值呈现显著的时变特性，服役0～110年，损伤值总体上呈线性上升，主要是由于结构主体处于弹性阶段；结构服役120～150年时损伤值也呈上升趋势，但增长速率明显随时间激增，第150年时的损伤值相较于设计值增长40%以上。在刚通车时，润扬斜拉桥若遭遇该地震波的破坏情况为中等破坏，而在150年时结构的破坏接近严重破坏。总体而言，润扬斜拉桥在7级EI Centro Site地震波作用下结构的地震损伤情况与结构疲劳损伤累积及结构性能劣化的规律有明显的一致性。

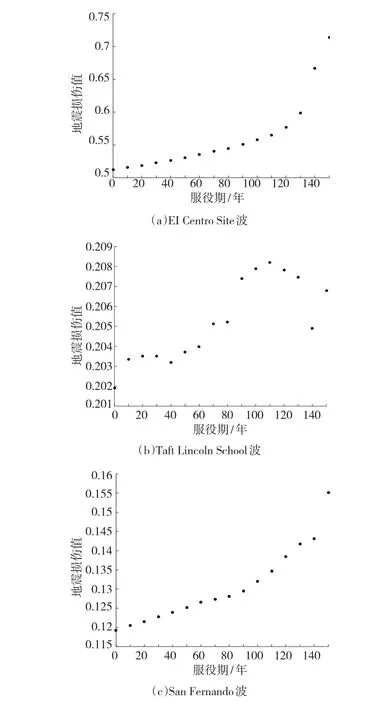
图6 多遇地震作用下结构时变损伤值

图6（b）是7级Taft Lincoln School地震波作用下的润扬斜拉桥地震损伤时变值。可以看出，损伤值变化不大但基本呈上升趋势，不过呈现的趋势并不明显，这与EI Centro Site地震波并不相同，可能是因为Taft Lincdn School波的振动模式与EL Centro Site波不同而导致结构的振型发生变化。桥梁在Taft Lincoln School地震波下的破坏情况为轻微破坏。

图6（c）是7级San Fernando地震波作用下的润扬斜拉桥地震损伤时变值。可以看出，损伤值也呈现出显著的时变特性，在服役期内结构损伤值总体上呈线性上升，第150年时的损伤值相较于设计值增长了30%左右。但该工况下，在服役150年时结构的破坏情况仍处于轻微破坏，这主要是因为San Fernando地震波达到时程加速度峰值的时间点很少，而且其他时间点的加速度值均明显小于加速度峰值。

从上述分析可以看出，润扬斜拉桥在各个地震波作用下结构的动力响应和破坏情况略有不同。随着材料性能的不断劣化，地震损伤不断加剧，服役期间的时变地震损伤值均大于设计损伤值，其中服役150年后在7级EI Centro Site波作用下地震损伤值相较于设计值甚至增长40%以上。不过在各个服役期时润扬斜拉桥在各个地震波作用下结构均不会发生倒塌。

4 罕遇地震作用下润扬斜拉桥的地震损伤时变性能分析

根据抗震规范规定，调整各地震波的加速度时程峰值，采用与上述多遇地震相同的方法研究罕遇地震作用下润扬斜拉桥的地震损伤时变性能。

图7给出了不同服役时间点（服役第0年、50年、100年和150年)遭遇9级El Centro Site地震波时，润扬斜拉桥横桥向和纵桥向的位移时程曲线。可以发现，El Centro Site波下结构在服役0年、50年和100年振动形态稳定，可见在50年和100年时刻时，虽然材料力学性能发生一定程度的劣化，但结构的振型没有改变，并且根据式（4）可得出在该工况下，结构处于严重破坏的状态，但并没有发展到倒塌的破坏程度。而在150年时，结构在地震作用下已经进入塑性，结构的振动形态相比之前发生变化，且在这个工况下，结构很有可能会发生倒塌。

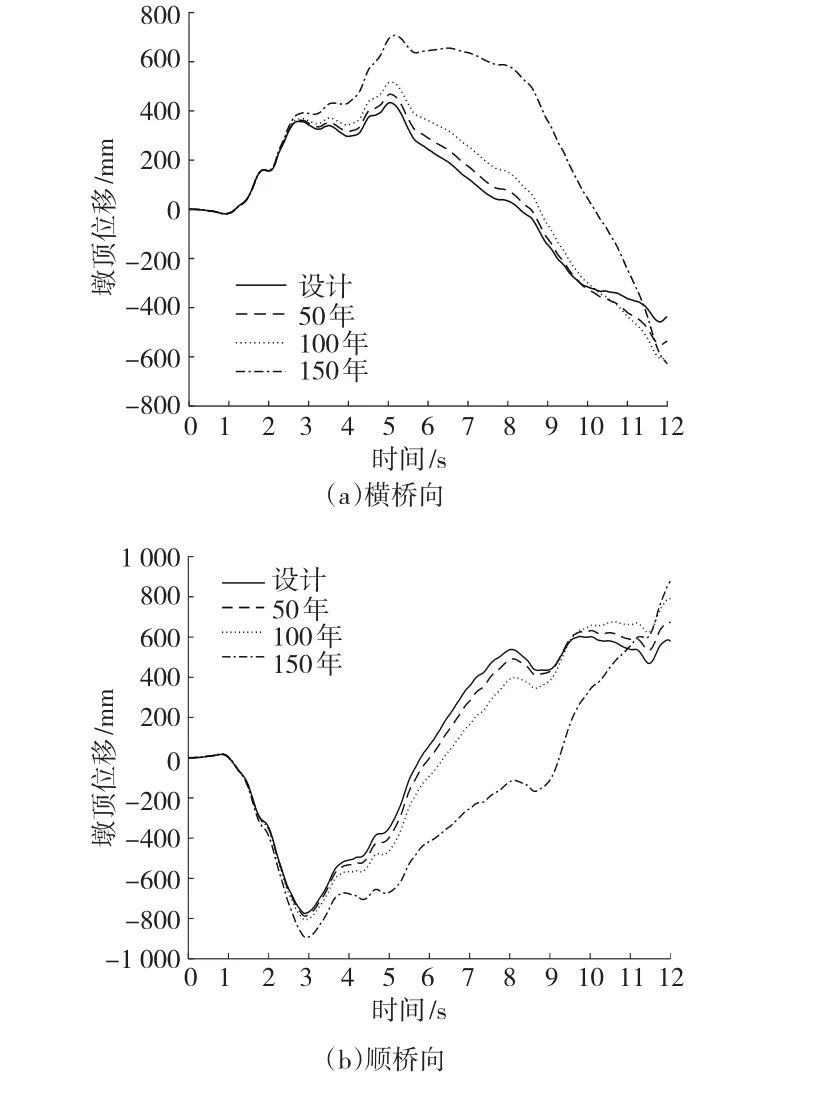
图7 9级El-Centro地震波下桥墩位移时程图

与第4节中多遇地震作用下一样，取横桥向和顺桥向的位移系数为0.8和0.6进行组合，得到罕遇地震作用下的桥墩顶部总的最大位移值，将每10年的最大位移值输入式（4）得到地震时变损伤值。图8给出了润扬斜拉桥在各服役期内突遭9级的EI Centro Site地震波、Taft Lincoln School地震波和San Fernando地震波，采用上述损伤状态的评估模型得到的地震时变损伤值。

图8 罕遇地震作用下结构时变损伤值

从图8中可以发现，与多遇地震作用下不同，润扬斜拉桥的地震损伤值的趋势并非总是呈现出上升趋势，即桥梁的抗震性能随着桥梁疲劳损伤累积的一致性并不明显，可能是由于局部构件随服役期的增长而逐渐进入塑性阶段。与多遇地震作用相同的是，9级EI Centro Site地震波作用下的结构地震损伤值明显大于相同等级Taft Lincoln School地震波和San Fernando地震波作用下的损伤值。

图8(a)是9级EI Centro Site地震波作用下的时变损伤值。可以看出，损伤值呈现较为明显的时变特性，损伤值总体上呈线性上升，第150年时的损伤值相较于设计值增长了30%以上。在刚通车时，润扬斜拉桥若遭遇该地震波还未达到倒塌破坏的程度，而在110年后的结构地震损伤值超过了表1中结构倒塌的抗震指标限值2.65%，表明若桥梁遭遇该工况的地震波，可能会发生倒塌。总体而言，润扬斜拉桥在EI Centro Site地震波作用下结构的地震损伤情况与结构疲劳损伤累积及结构的性能劣化规律基本一致。

图8（b）是Taft Lincoln School地震波作用下的润扬斜拉桥地震损伤时变值。可以看出，损伤值变化不大但是几乎没有特定的规律性，这与EI Centro Site地震波和San Fernando地震波的情况并不相符，主要可能因为Taft Lincoln School波的振动模式与EL Centro Site波和San Fernando波不同而导致结构的振型发生变化，或者因为各个构件强度不同，导致在各服役期内某些强度低的构件发生塑性变形，使得在地震载荷作用下的受力分配情况发生改变。在各服役期内，润扬斜拉桥在Taft Lincoln School地震波作用下的破坏情况为严重破坏，但其损伤值离发生倒塌事故还相差甚远。

图8（c）是San Fernando地震波作用下的润扬斜拉桥地震损伤时变值。可以看出，损伤值呈现出显著的时变特性，在服役期内结构损伤值呈线性上升。第150年时的损伤值相较于设计值增长了30%左右。但该工况下，在服役150年时结构处于中等破坏，这主要是因为San Fernando地震波达到时程加速度峰值的时间点很少，而且其他时间点的加速度值均明显小于加速度峰值，导致结构在该工况下的损伤值明显小于上述两种地震波。

上述分析可以看出，润扬斜拉桥在各个地震波作用下结构的动力响应和破坏情况虽然有明显的不同，但由于材料性能的不断劣化，结构的地震损伤情况基本上不断加剧，而且有发生倒塌事故的可能。

5 结论

本文面向桥梁抗震性能分析，研究了其疲劳损伤时变特性，基于动力弹塑性时程分析法获得结构在不同服役年限时遭遇多遇和罕遇地震时的响应，依据桥梁性能对照标准和地震损伤模型，研究了桥梁抗震性能的时变特性。以润扬长江大桥北汊斜拉桥为研究对象，获得了如下主要结论：

（1）考虑材料的性能劣化和损伤的时变特征，可以更为准确地分析和评估大跨桥梁在地震荷载作用下的抗震性能。

（2）多遇地震作用下润扬斜拉桥在服役前期，各构件仍处于弹性状态，振动形态稳定，而在服役后期，局部构件进入塑性，结构的振动形态相比之前发生变化，不过，在各服役期内润扬斜拉桥在各个地震波作用下结构均不会发生倒塌。

（3）罕遇地震作用下润扬斜拉桥在服役前期的振动形态仍较为稳定，未达到倒塌的破坏程度。而在服役后期，结构在地震作用下已经进入塑性，振动形态相比之前发生变化，结构很有可能会发生倒塌。

总而言之，进行考虑损伤时变特性的桥梁抗震分析对于服役期长且重要的大跨桥梁而言是必要的甚至是不可或缺的。

参考文献

[1]缪海萍.服役载荷作用下的钢桥疲劳损伤预后分析方法[D].南京：东南大学，2013.

[2]重庆交通科研设计院.公路桥梁抗震设计细则[M].北京：人民交通出版社，2008.

[3]王振宇，刘晶波.建筑结构地震损伤评估的研究进展[J].世界地震工程，2001，17（3）：43-48.

[4]沈祖炎，董宝，曹文衔.结构损伤累积分析的研究现状和存在的问题[J].同济大学学报自然科学版，1997（2）：135-140.

[5]陆本燕，刘伯权，吴涛，等.基于RC桥梁墩柱的地震损伤模型比较分析[J].土木工程学报，2010（s1）：186-191.

[6]孙颖，卓卫东，房贞政.规则桥梁抗震性能水准的定义及其量化描述[J].地震工程与工程振动，2011，31（5）：104-112.

[7]Kim T H，Lee K M，Chung Y S，et al. Seismic damage assessment of reinforced concrete bridge columns[J].Engineering Structures，2005，27（4）：576-592.

[8]Li Z X，Chan T H T，Ko J M. Fatigue analysis and life prediction of bridges with structural health monitoring datapart I：methodology and strategy[J]. International Journal of Fatigue，2001，23（1）：45-53.

[9]Chan T H，Li Z X，Ko J M. Fatigue analysis and life prediction of bridges with structural health monitoring data-partⅡ：application[J]. International Journal of Fatigue，2001， 23（1）：55-64.

[10]Lemaitre J. Evaluation of Dissipation and Damage in Metals Submitted to Dynamic Loading[C]∥Proceedings of ICM-1，Kyoto，Japan，1971.

[11]孙正华，李兆霞.润扬斜拉桥有限元模拟及模态分析[J].地震工程与工程振动，2006，26（2）：25-32.