钛镍合金固体火箭发动机一维非稳态导热及热应力研究

2018-05-11南昌航空大学飞行器工程学院南昌330063薛志远胡晓安

石河子科技 2018年1期

（南昌航空大学飞行器工程学院，南昌，330063）薛志远胡晓安

钛镍合金（TiNi）是近年来比较热门的金属材料，正被广泛运用于电子、机械、医疗、能源、航空航天等领域。钛镍合金最为显著的优点是比强度高和耐腐蚀性好，具有优良的形状记忆和超弹性，具有比较好的机械性能，晶粒度很细小，可以被加工成很细小的丝材和薄板[1]。由于钛合金具有优异的热强度以及较高的比强度，耐高温，高温环境下化学稳定性好，得以在发动机上被逐渐使用。未来的航空航天飞行器及其推力系统需要拥有更高强度的、更高工作温度、更高弹性模量、密度更高且更加经济的材料，钛镍高温合金便成了主要的材料选择对象之一。

基于厚壁圆筒温度分布以及热应力的研究国内外学者已经做了诸多探索。美国学者Paton，Koppel[2]等人在上世纪八十年代对电感加热器以及核燃料元件装置建立厚壁圆筒模型，给出了具有内热源的圆筒热应力计算通式。日本学者平修二[3]在上世纪八十年代末，为了强化当时工程技术人员对于设计制造高温高压下使用的动力机械或化学反应装置的热疲劳以及高温强度的理解，依据日本材料协会高温强度委员会有关热应力和热疲劳方面的研究成果，在对高温下机械设备破损原因进行大量分析之后，出版了《热应力与热疲劳》一书，系统阐述了热应力分析方法，并广泛涉及了基础理论和设计应用；丸山武志[4]等人完善了关于多层圆通导热系数的测定方法以及不稳定温度分布理论，该方法适用于高压下测定各种多层化学反应容器的导热系数的测定，同时对容器壁厚没有限制，具有较高的经济性和适用性，不稳定温度分布理论可以帮助测定容器焊接接头附近由于温度差引起的热应力，导热系数的方法，为后来开展圆筒导热研究奠定了基础。在国内，国防科技大学教授孟祥贵[5]等人为了对厚壁圆筒在受到温度场的作用时在内部产生的热应力进行精确分析，提出关于圆筒热应力问题的传递函数方法，该传递函数方法具有较大的灵活性和适应性；青海师范大学杨能彪[3]等人针对瞬态导热过程中，由于时间因素相关的非稳态项是对时间的导数问题，给出了一维瞬态导热问题的数值解答。

由于目前针对固体发动机各典型截面在非设计状态（启动过程）中，经受瞬态温度（物体内部各点温度随时间改变叫做瞬态温度，这种变化的温度的热量传递过程称为非稳态热传导）载荷条件下的瞬态温度场以及热应力分析还有待进一步的研究，利用等厚壁圆筒简化模型，通过研究以钛镍基合金为材料的某型固体发动机瞬态温度和热应力分布，为固体发动机实验时一维非稳态导热和热应力计算提供基本思路，同时也加深对解钛镍合金的认识，推动钛镍合金在发动机领域的运用。

1 传热分析模型

1.1 物理模型

固体火箭发动机燃烧室、发动机喉部以及发动机喉部出口某截面，认为温度与周向和轴向无关，只是径向坐标的函数，从而简化为等厚壁圆筒。参照某型固体火箭发动机结构尺寸，该等厚壁圆筒内径ra=1.8m，外径rb=2m。圆筒结构如图1所。圆筒内壁为高温燃气，由于发动机燃烧室、发动机喉部以及发动机喉部有不同的工作温度，因而所选取的典型截面处具有不同的瞬态温度值。内壁有高温燃气充当内热源，给定瞬态温度边界值。外壁与外界大气相接触，存在对流换热。

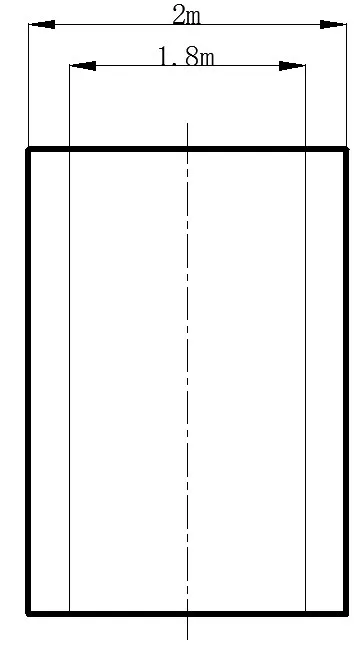
图1 圆筒结构平面图

1.2 物理模型的简化

该等厚壁圆通为轴对称旋转体结构，各典型截面所在圆筒温度在轴向上无变化，温度分布只与半径和时间有关，故可以把圆筒投影到平面上。于是，该固体发动机导热问题便简化为一维下的非稳态导热。简化后的圆筒一维模型在极坐标中进行分析，如图2所示。

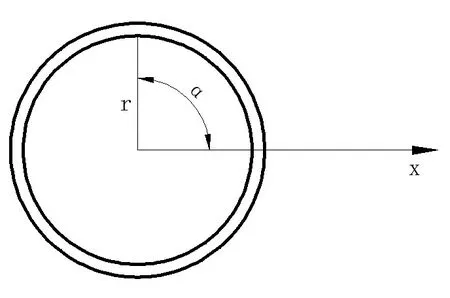
图2 简化后的圆筒一维模型在极坐标中分析图

1.3 钛镍合金材料热物性参数

通常在实际工程材料中，对于金属材料而言，其物理性质大多和温度以及物质的种类有关。由于发动机启动过程温度变化范围很大，采用线性近似关系来确定相关热物性。一般而言，热膨胀系数主体上随温度升高从而线性增大，弹性模量随着温度的增加而大幅下降，泊松比随温度变化不明显，导热系数随着温度上升趋于降低，定压比热在温度上升时也相应增加[6]。这些参数均可作为温度的线性函数。在非稳态过程导热中，当给定初始条件和边界条件时，导热过程受材料热物性中的导热系数的影响十分明显，特别是当导热系数是温度的函数时，导热过程遭受的影响更加显著[6]。在温度变化较大的发动机启动工况下，故弹性模量、导热系数、热膨胀系数、定压比热以及换热系数分别表示为E、λ、α、Cp、h，它们均为温度的函数查材料参数手册，相应温度下钛镍合金的热物性参数如下表1所示，其余时刻对应温度下的材料热物性采用线性方法进行材料参数的内插和外推得到。钛镍合金密度为ρ=4.5*103kg/m3，密度为定值，不随温度变化。

1.4 基本假设

该等厚壁圆筒属于轴对称结构，圆筒轴向上横截面积为定值，各典型截面所在圆筒上的温度在轴向上不发生变化，因而可取某个截面进行分析。温度随时间不断变化的非稳态过程；该圆筒内壁均匀受热，为纯导热作用没有对流，按第一类边界条件处理；外表面与外界干空气接触，涉及对流换热，采用第三类边界条件。圆环初始温度场为外界干空气温度，取为T0=Ta0=Tb0=288K。

2 导热过程的计算分析

当相位角ϕ=π/2时，圆环非稳态导热方程为

表1 材料热物性参数

给定初始条件：当t=0时，T=T0

边界条件：

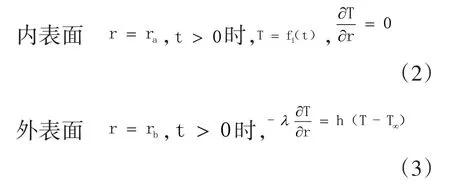
其中，T∞为外部大气温度

3 数值离散

对时间坐标进行考虑，因而一维瞬态导热就变成了二维问题，拥有时间坐标t和空间坐标r两个变量。但是时间坐标t是单向的，也就是前一时刻的状态只能对后一时刻的状态产生影响，反之则不产生影响。图3显示出了以r和t为坐标的环形区域的离散，时间t从0时刻开始，增量步为20s，经过一个个时层增加到k、k+1时层[7]。

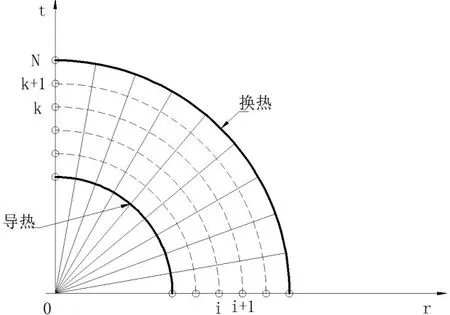
图3 r-t环形区域的离散

3.1 微分方程的离散

对导热方程（1）进行数值离散，则可得到离散的控制方程：

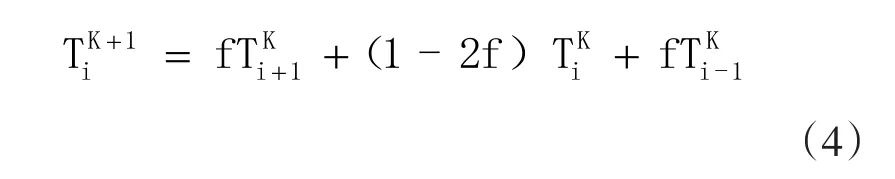
3.2 边界条件的离散

用K+1时刻相应节点的差分，替换式（2）（3）中的微分，得到边界节点的差分方程显式解：

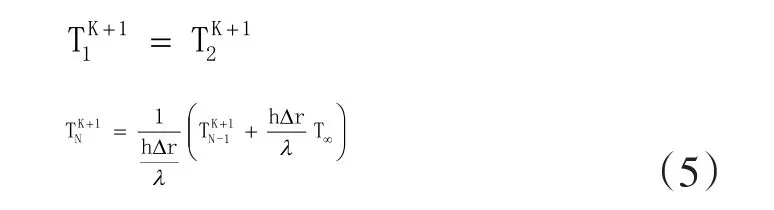
4 各典型截面的温度场的计算

参照某型固体发动机实际工况，计算等厚壁固体发动机圆筒各典型截面各节点的温度值，并和ABAQUS计算得到的温度值进行对比，以论证数值计算结果的准确性。

4.1 该型固体发动机地面试车设计点飞行条件

Ma=0，H=0，T0=288K。稳定工作时燃烧室出口温度为T4=1182K。

地面试车时，启动工况是发动机从停止状态到稳定运行状态的过渡过程，此过渡过程每一瞬时的燃气温度、负荷都不相同，圆筒内侧边界温度以及外侧边界换热条件都和时间有关，因而这一过渡阶段是非稳态的，本论文对这一阶段进行研究。

4.2 各典型截参考节点的温度值

将表1数据代入式（4）（5）中得各截面各节点的温度分布，其中，i=1,2,…,6，K=0,1,2…,13。利用MATLAB绘制出各典型截面上不同位置节点处温度随时间变化图像如图4所示：

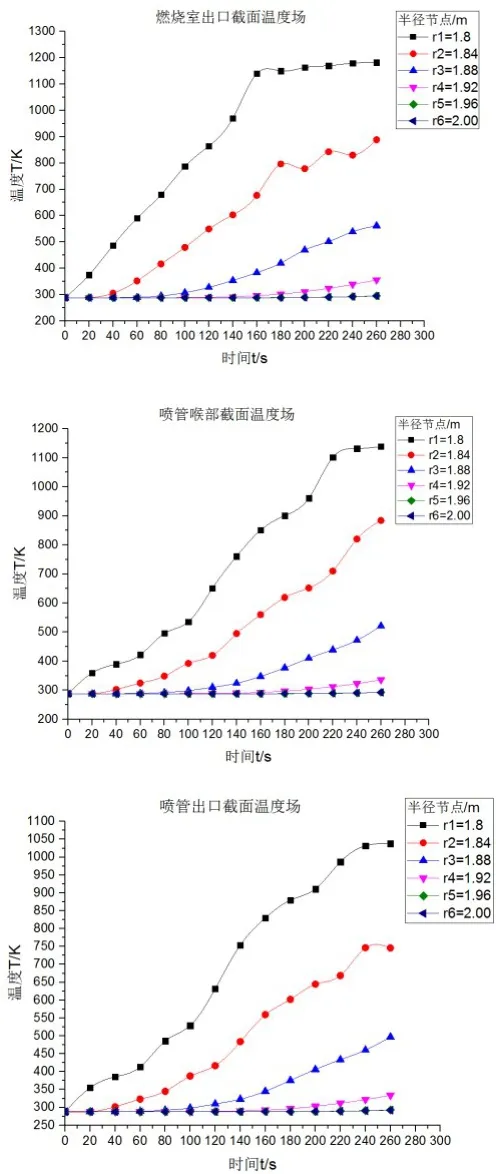
图4 燃烧室出口、喷管喉部、喷管出口截面各参考节点温度曲线图

4.3 应用ABAQUS对各典型截面进行温度场分析

如图5、图6、图7各典型截面温度场分布云图所示。可见各截面瞬态温度场分布和实际数值计算所得温度分布大致相同。

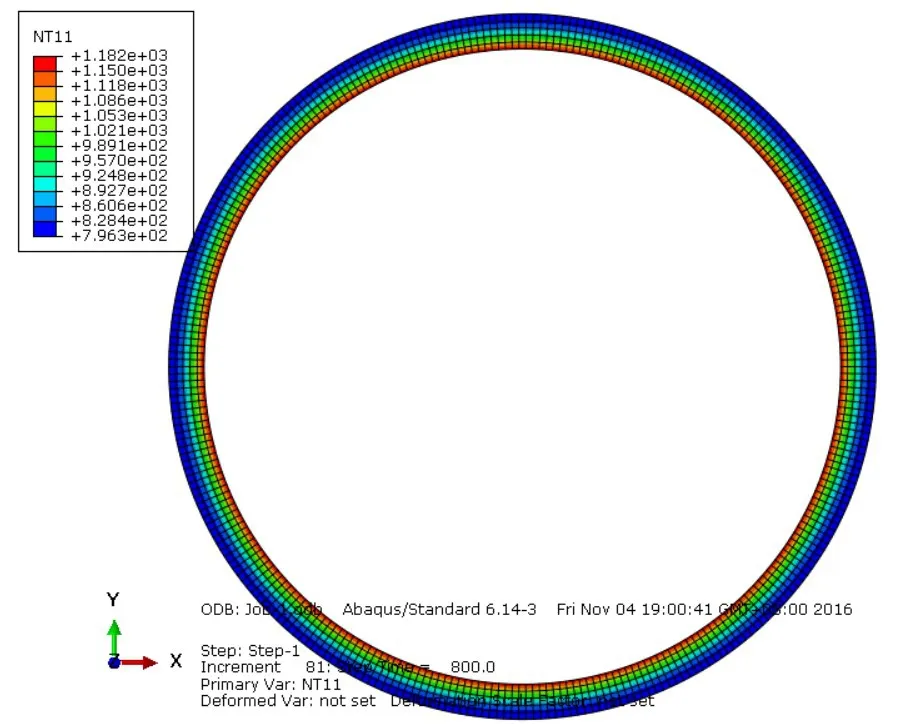
图5 发动机燃烧室截面温度场

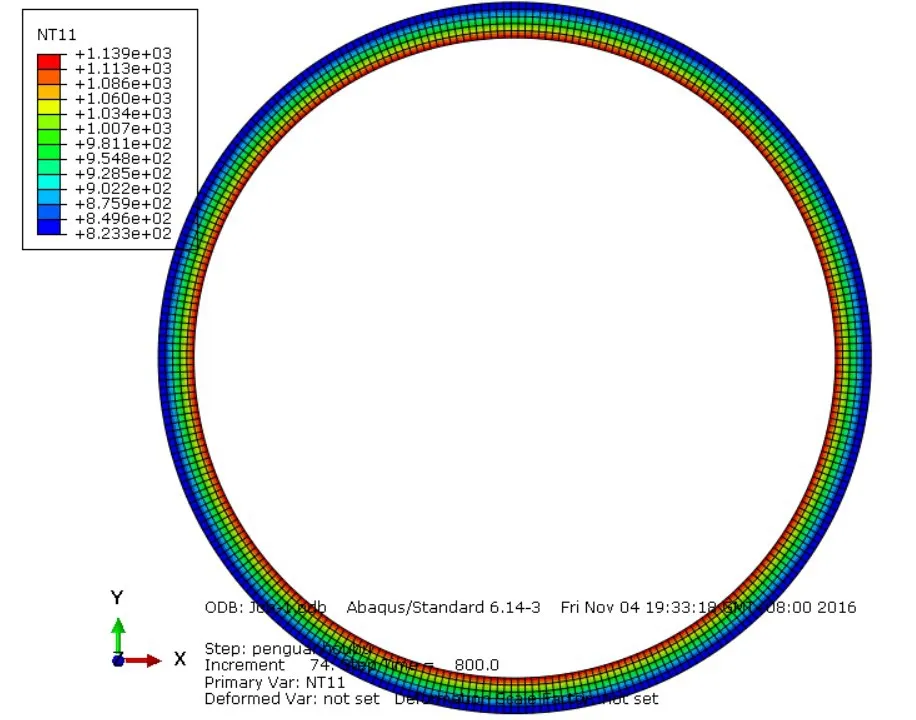
图6 喷管喉部截面温度场

5 基于MATLAB的等厚壁圆桶热应力计算分析

物体由于热变形使受约束物体内产生的应力称为热应力。热应力的产生有两种原因：结构内外表面受热不均，产生温度梯度；受到外部约束，这样热变形就要受到内部各部分的相互制约和外界的限制，从而产生热应力。等厚壁圆筒形结构，内部存在高温气体作为热源，内外表面形成温度梯度，因而产生了较大的热应力[6]。

不考虑轴向应力，圆筒径向、周向应力关于温度的函数如下：

径向应力：

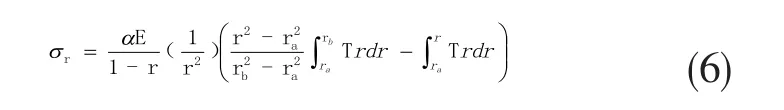
周向应力：

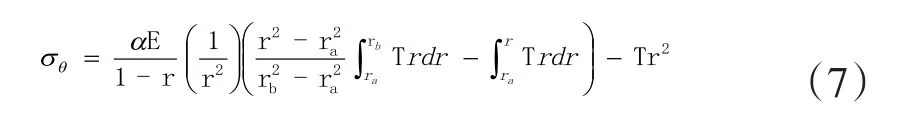
其中，a为热膨胀系数，ra为圆筒内径，rb为圆桶外径，E为弹性模量。利用MATLAB编制径向与周向热应力计算程序，即把由（4）（5）式得到的各节点，运用曲线拟合法，得到同一时刻径向上各个节点温度值关于半径r的函数关系，再代入（6）（7）式中即可得到相应的径向热应力和周向应力，热应力随时间变化的关系曲线如下图8、图9、图10所示。

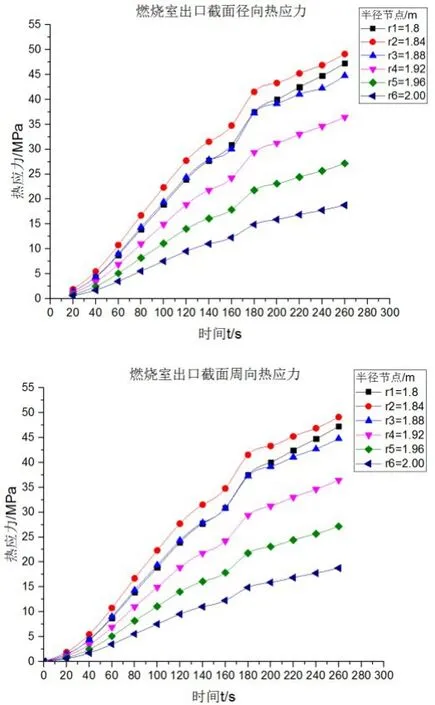
图8 燃烧室出口截面半径方向上各节点径向、周向热应力

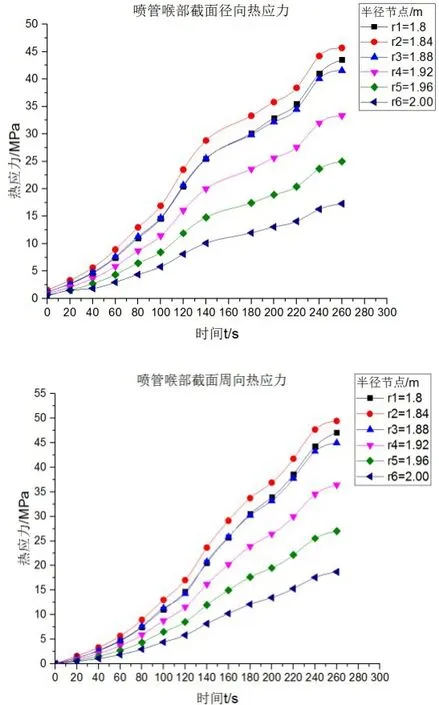
图9 喷管喉部截面半径方向上各节点径向、周向热应力

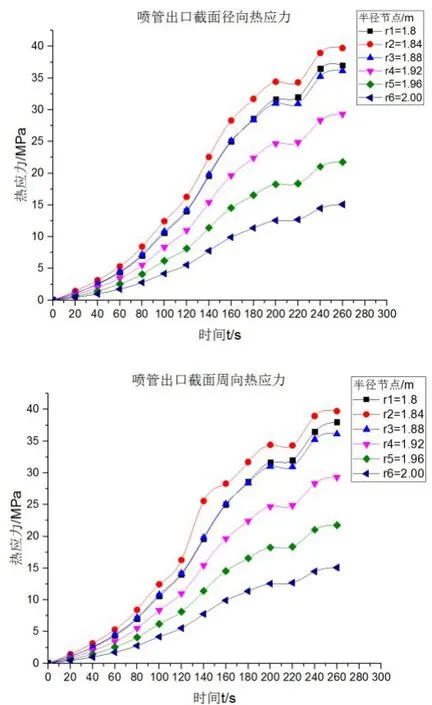
图10 喷管出口截面半径方向上各节点径向、周向热应力

6 讨论

基于传热学理论，参考单层无限长圆筒的温度分布一般情况，对一维圆筒模型的非稳态导热方程用差分法进行数值离散，借助于MATLAB计算出圆筒半径方向上所选取的节点各时间节点处的瞬态温度解析计算值，同时用ABAQUS有限元分析软件对圆筒导热过程进行模拟得到瞬态温度场的有限元解法，与解析计算结果进行比较。再采用曲线拟合的方法，得到发动机启动时各个考察时间点上，半径方向上各节点温度值T关于圆筒半径r的函数关系，再代入圆筒热应力计算公式（6）、（7）中，利用MATLAB编写程序，计算得到径向热应力和周向热应力。

考虑了第一类和第三类边界条件，即规定圆筒内侧温度随时间变化，圆筒外侧与外界干空气表面传热系数h以及周围空气的温度。圆筒内部高温燃气充当内热源。但是，在固体发动机实际工作过程中，热传递将变得更为复杂，为了更好的对固体发动机筒壁进行温度场和热应力测定分析，还应当考虑辐射换热以及不同的升温速率对温度场和热应力的影响。因为篇幅限制，本论文也只考虑了启动工作状态下的非稳态导热传热过程，更好的改进方法是对固体发动机停止过程的非稳态导热过程进行热应力分析。同时可以在本文一维非稳态基础上进行多维非稳态导热及热应力的分析计算，由此才能够更接近实际工况，获得更为精确的瞬态温度以及瞬态热应力，同时也能够更好的论证某种材料在固体发动机上运用的可行性，以达到固体火箭发动机地面试车的实验热应力计算分析的要求。