化工行业电气仪表温度参数的自整定方法

申军祥

（山西省阳煤集团平定化工有限责任公司,山西 阳泉 045000）

引 言

化工行业是一个比较重要的行业,对我国各方面的发展都有着非常积极的意义。化工行业对最终实验结果的精确度要求比较高,但化学实验往往会受到外界各种各样因素的干扰,因此,我们必须做好相应的控制工作,从而保证最终结果的准确性。在化工行业领域内,电气仪表温度参数的测量一直受到广大工作者的关注。化工行业所涉及的仪表元件比较复杂,其温度参数会受到外界因素的干扰,存在一些误差,对电气仪表温度参数的控制和测量必须避免这些误差,才能达到最终的实验效果。从以往的设计思路看,工作人员对于精确度的认识往往是通过自整定反馈进行的,在以往传统的自整定方法中,工作人员对电气仪表温度参数的控制方法大致可以分为三大类。这些方法从本质上说都是基于不同的载体而进行的参数自整定反馈模式,从细节来看,这些方法的基本原理都是通过构建电气仪表温度参数的反馈校正模型,选定一些比较精确的参数,随之进行相应的实验测试,从而得出比较准确的数据。从以往的研究成果来看,曾有学者提出采用不确定边界的自适应误差补偿方法,这种方法有其优越的一面,它可以极大程度地避免仪器受温度的影响,测量的精度也会随之增高,但是这种方法的计算经济性不高,花费较大,而且时效性不强。针对这一缺点,之后的学者通过深入的研究,提出了鲁棒自适应的方法,该方法也有其优越的一面,它可以通过建立稳态方程式从而实现参数自整定性的控制,其精确度非常高,但是这种方法也有着一定的弊端,它容易受到不确定非线性温度突变的干扰,有一定的不稳定性。随后,又有学者采用了电阻接地的计算方法,这种方法也有着比较大的缺陷,一旦仪表温度参数超限,就会导致测量精度的下降。由于化工行业对最终实验结果的要求比较高,而本行业的特点却是充满了不确定性,极易受到外界不确定因素的干扰,造成一定的实验误差,以往学者对其进行了摸索和尝试,虽然有了很大的进步,但是方法的弊端依然存在。鉴于此,本文从理论入手,构建出了一种新的模式,吸纳以前方法中的优点,设计了PID控制器,希望能够推动化工行业的发展。

1 温度参数自整定的构建

1.1 构建反馈校正模型的相关思路

在进行此项设计工作之前,首先要规划和设计电气仪表温度测量控制模型。从化工行业的工艺流程来看,化工行业的温度测量一般采用的是闭环串连反馈控制装置,其调节器是一个非常复杂的结构,可以大致分为比例控制、微分控制和积分控制3种,其PID控制从整体来说是非常模糊不清的［1］。具体工作原理见图1所示。

图1 电气仪表温度测量的模型

图1中,r是电气仪表温度测量系统的前端输入口,末端的y则为输出端,而d则为一些未知条件的干扰因素。在图1的中部,P（s）为温度测量过程中的传递函数,M（s）为电气仪表温度测量过程中一些固定频率的值,Q（s）等值表示的是测量过程中的容错系数。

通过一系列的计算,我们可以得到,在函数的表达式中,可以假设其传感器采样的周期为T,通过带入计算和进一步的化简,可以推导出公式（1）。

式中,E则表示温度参数幅频的函数,其表达的意思可以描述为根据振荡抑制和并联校正,这个过程可以完整地实现反馈校正的全过程,而且其精度也是比较高的,可以为进一步的工作提供一定的数据支持。

1.2 自整定控制的相关分析

自整定控制设计是一个比较复杂的过程,首先,应当进行反馈校正传递模型的构建和计算,接着,研究和分析出具体的自整定控制的约束值。在这样的整体思路下,可以得出自整定控制的三通模型［2］,见式（2）。

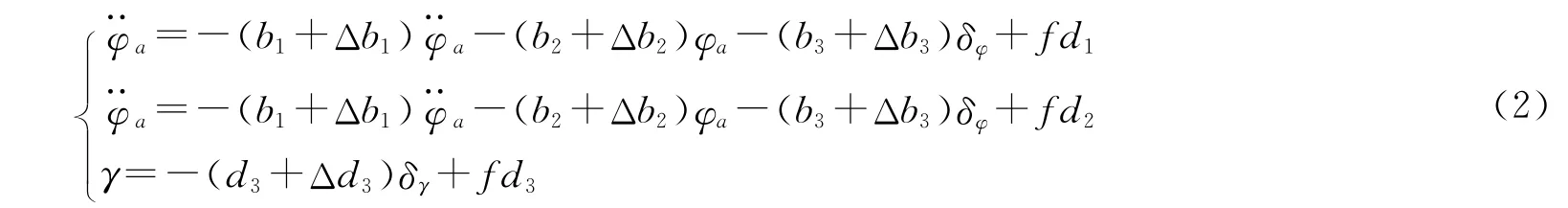
但是,从本质上分析,式（2）还存在着一定的模糊性,对其进行进一步的整理,得式（3）。

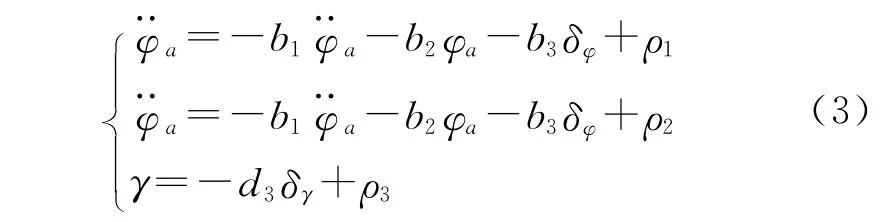
在整体设计的过程中,为了进一步保证最终实验结果的准确性和稳定性,还需设计误差补偿的过程,具体描述为式（4）。

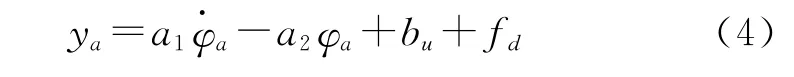
在误差补偿的基础上,对三通道模型进行了进一步的整合,可以推导出其约束模型,见式（5）。

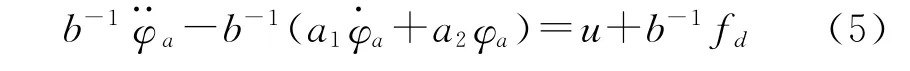
综合以上推导公式,可以得到最后的约束模型为式（6）。

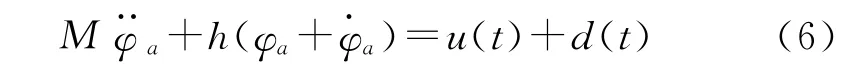
在这个公式的引导下,自整定过程可以顺利的实现,也为化工行业进一步的技术优化提供了现实可能性。

2 自整定方法的设计和阐述

在PID的设计过程中,首先假设控制约束目标函数为M,我们所需要的目标函数包括2个部分［3］,具体可以描述为式（7）、式（8）。

最终根据这些原理可以设计出PID控制器的相关内容,具体见图2所示。

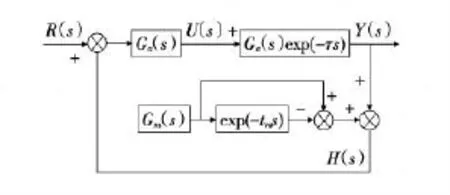
图2 PID控制器设计

3 仿真实验探究

在进行电气仪表温度参数的自整定方法设计后,可以通过一系列的仿真实验进行验证,从而证实其优越性。在仿真实验中,我们可以借助先进的数学仿真工具进行测验,并实时记录结果［4］。并对PID函数进行归结,具体见式（9）。

对这个原理首先进行了电气仪表的误差分析,得出2种不同的结果,见第88页图3所示。

从图3中可以看出,经过参数的自整定处理之后,电气仪表测量温度的准确性得到了进一步的提高,其误差也比较小,稳定性也有了明显的改善。

仿真实验结果也从侧面印证了结论的正确性。同时,以温度的输出参量作为变量进行了实验,通过对比,得到了对比分析图,如第88页图4。通过对比图,可以清晰地看出,采用本文论述的测量模式可以有效地降低温度漂移以及稳态误差对测量结果的干扰,降低了振荡的幅度,大大提升了控制的精度,对于化工行业有着非常积极的意义［5］。

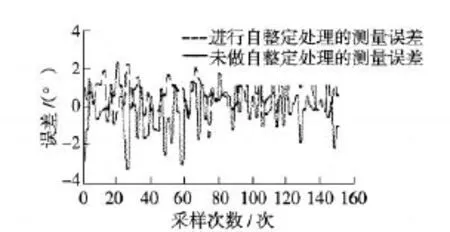
图3 误差对比分析图

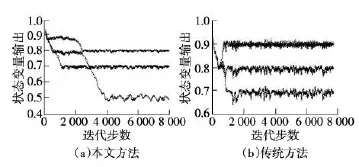
图4 温度控制器变量输出的对比

4 结语

为了优化化工行业电气仪表稳定性和有效性的问题,本文从实际出发,结合相应的理论背景,通过一定的温度参数自整定性控制研究,大大降低了外界温度以及其他条件对最终结果的振荡和干扰,提升了最终测量结果的精确度。在此次实验中,结合以往设计的优缺点,进行了新的设计,即设计了PID控制器,进行了一系列的多模稳态自适应整定性的控制,从而对传统方法进行了进一步的改革和创新。在这样的方法下,化工行业电气仪表温度测量的精度得到了很大的提升,其抗外界干扰的能力也进一步加强,能够很好地避免温度漂移失真的现象,大大提升了电气仪器设备的可靠性。此方法可以进行推广。

参考文献：

［1］ 徐栋.化工行业电气仪表温度参数的自整定方法［J/OL］.西安工程大学学报,2016,30（5）：603－608,615.

［2］ 朱广晶.化工行业电气仪表使用安装核心技术问题及方法［J］.中小企业管理与科技,2016（3）：293.

［3］ 徐栋.化工行业电气仪表使用安装核心技术问题及研究［J］.当代化工研究,2016（7）：94－95.

［4］ 段广照,景阳阳.化工行业电气仪表使用安装关键技术问题及措施分析［J/OL］.电子技术与软件工程,2015（15）：123.

［5］ 叶林.化工行业电气仪表使用安装关键技术问题及措施分析［J］.中国石油和化工标准与质量,2014,34（3）：35.