基本蚁群算法在解决TSP问题中参数选择的研究

◆杨昌昊 张 琢

基本蚁群算法在解决TSP问题中参数选择的研究

◆杨昌昊 张 琢

（东北师范大学信息科学与技术学院 吉林 130117）

蚁群算法是受自然界中真实蚁群觅食行为的启发而提出的一种优化算法，基本蚁群算法是其中基础且较为经典的一种算法，而基本蚁群算法中的参数对算法效果有很大的影响。本文以使用基本蚁群算法解决TSP问题为例，在对相关内容进行介绍后，进而对基本蚁群算法的参数选择进行了实验及分析，最终给出了基本蚁群算法中各个参数的基本选择范围。

蚁群算法；基本蚁群算法；TSP问题

0 引言

启发式算法(Heuristic algorithm)是一类基于生物学、物理学和人工智能的，具有全局优化性能、鲁棒性强、通用性强且适用于并行处理的算法[1]。现阶段，启发式算法以仿生优化算法[2]为主，主要包括模拟退火算法[3]、粒子群算法[4]、遗传算法[5]、混合蛙跳算法[6]、蚁群算法等。

蚁群算法(Ant colony optimization algorithm)是受自然界中真实蚁群觅食行为的启发，发现虽然单个蚂蚁没有太多的智力，也无法掌握附近的地理信息，但整个蚁群却可以找到一条从巢穴到食物源之间的最优路线而提出的一种仿生优化算法[7]。

在蚁群算法的研究中，研究者们常以TSP问题作为该算法的运行实例。TSP (Traveling salesman problem)问题又称为旅行商问题，是一种比较经典的NP难题，问题描述较简单，而获得最优解却十分困难。求解TSP问题不仅为其他算法提供了使用平台，而且算法的优劣性能也可通过其求得TSP问题的解集来验证。TSP问题的经典描述为：已知N个城市及相互间的距离，旅行商从某城市出发遍历这N个城市后再回到原点，在旅行商每个城市都只访问一次的前提下确定一条最短路径[8]。本文也将以TSP问题作为基本蚁群算法中对参数设计方案进行验证的运行实例。

基本蚁群算法是蚁群算法中最经典且基础的一种，在使用基本蚁群算法解决TSP问题时，算法中的各个参数对算法的效果有很大影响，在Wei Xianmin所著论文[9]中便提到了蚁群数量、信息素重要程度系数及两城市间距离重要程度系数三个参数算法效果的影响，并给出了实验数据。但对于全部参数对算法的影响情况，目前暂未有论文进行实验论证。

因此，本文将对基本蚁群算法的执行流程、影响算法执行的参数进行介绍，并对相关参数进行一系列实验与分析，最终得出使用基本蚁群算法解决TSP问题时参数的基本选择范围。

1 基本蚁群算法模型介绍

1.1基本蚁群算法简介

基本蚁群算法通过模拟自然界的蚂蚁觅食过程对目标进行搜索，人工蚂蚁会根据路径上的信息素浓度的函数，按概率选择下一个将要访问的城市，信息素浓度越高，则该路径被选择的概率越大。当人工蚂蚁进行完一次循环后，其会在其访问过的每条边上都留下相应的信息素。

1.2基本蚁群算法执行流程

（1）初始化

算法开始时，将m只蚂蚁随机的放到n座城市中。将每只蚂蚁k的禁忌表tabuk的第一个元素设置为当前它所在的城市，下一步允许选择的城市表allowedk设为除当前它所在的城市外的所有城市。同时，将各条路径上的信息素量统一设为一较小的常数。该常数的选择有很多种方式，本文中选为1/(m*n)。

（2）每只蚂蚁独立的选择一次周游的路径

每只蚂蚁按照各条路径上的信息素量、两城市间的距离及其相关的参数独立的选择下一座城市。在时刻t，蚂蚁k在城市i上选择城市j的概率Pijk(t)为：

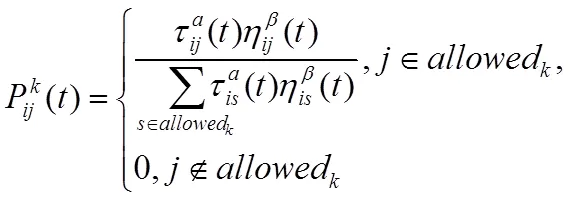
其中，allowedk表示蚂蚁k下一步允许选择的城市，即在所有城市中减去禁忌表tabuk中的城市，α代表信息素的相对重要程度，β代表两城市间距离的相对重要程度。

当allowedk变为空时，即完成了一次周游。

（3）每只蚂蚁独立的选择一次周游的路径

当全部m只蚂蚁都完成一次循环之后，各路径上的信息素将会根据下式进行更新：

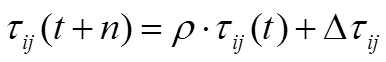
其中，ρ代表信息素的残留系数。关于Δτijk的计算方法，M.Dorigo给出了三种不同的实现方法，分别对应三种不同的蚂蚁系统模型[11]：Ant-cycle模型、Ant-density模型及Ant-quantity模型。它们的计算方法如下：

在Ant-quantity模型中：

在Ant-density模型中：

在Ant-cycle模型中：

上面的三个公式中，Q为一正常数，表示蚂蚁循环一周所释放的信息素总量。Lk表示蚂蚁k在本次循环中所经过的路径的长度。

2 基本蚁群算法中各参数对算法性能影响的研究

在蚁群算法中，算法运行参数的选取对算法性能有着至关重要的影响。对于不同的优化问题，算法的参数选取不同。即使对于同一类型优化问题，由于问题规模不一样，算法的参数选取也不尽相同[12]。

本文使用TSPLIB提供的att48数据集，针对基本蚁群算法中各个参数的不同取值进行了大量实验，意图找出参数选择的规律。

att48数据集包含美国本土48州州府的地理位置坐标，其最优解为10628。

2.1实验硬件、软件环境

实验使用MacBook Pro (Retina, 13-inch, Early 2013)型计算机，处理器为2.6 GHz Intel Core i5，内存为8 GB 1600 MHz DDR3。操作系统为macOS High Sierra 10.13.2，JDK版本为JDK 1.7.0_80。

2.2蚁群数量对算法性能的影响

蚁群算法是一种并行随机搜索算法, 它是通过多个候选解组成的群体进化过程来搜索最优解。蚁群数量越大可以提高蚁群算法的全局搜索能力以及算法的稳定性，但蚂蚁数目增加到一定程度以后，会使大量的曾被搜索过的解(路径)上的信息量的变化比较平均，信息正反馈的作用不明显，搜索的随机性增强，造成收敛速度变慢。反之，蚁群数量越小，特别是当要处理的问题规模比较大时，会使那些从来没被搜索到的路径上信息素量减小到接近0，搜索的随机性减弱，虽然收敛速度较快，但是会使算法的全局性能降低。

为了研究蚁群数量对算法性能的影响，将算法中其他的参数固定(采用Ant-quantity模型，迭代次数=100次，ρ=0.5，α=1.0，β=10，Q=10)，针对att48数据集，对不同的蚁群数量各进行10次测试，结果如下表1：

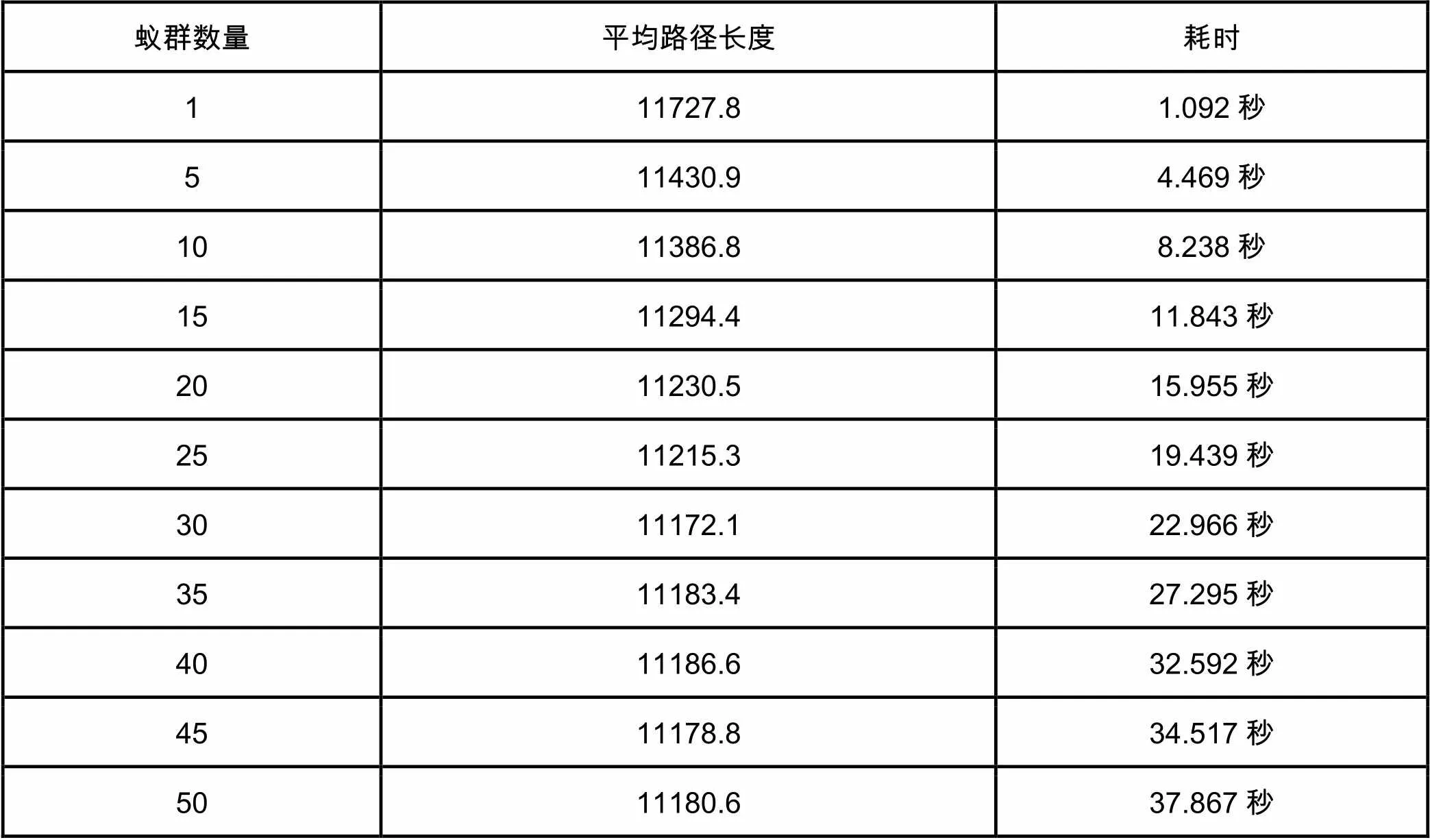
表1 蚁群数量对算法性能的影响

根据实验结果可见，当蚂蚁数量小于30时，随着蚁群数量的不断增大，100次迭代后得到的平均路径长度不断优化，而当蚂蚁数量超过30时，蚂蚁数量对于结果的影响开始变得不再那么明显。耗时方面，每增加5个蚂蚁，耗时约增加4秒。因而，针对att48数据集，考虑效果与耗时，可将蚂蚁数目设为30个，即约0.6倍的城市数目。

2.3算法模型对算法性能的影响

三种算法模型中，关于信息素增量的算法截然不同，因而可能会对算法结果产生较大的影响。

在Ant-quantity模型中，从城市i到城市j的蚂蚁在路径上的信息素增量为一个与路径无关的常量Q。在Ant-density模型中，从城市i到城市j的蚂蚁在路径上的信息素增量为Q/dij，dij为城市i到城市j的距离，因而信息素增量会随着城市间距离的不同而变化。在Ant-cycle模型中，从城市i到城市j的蚂蚁在路径上的信息素增量为Q/Lk，由于Lk为第k只蚂蚁在该次循环中所走过的路径的总长度，因此信息素增量与该次循环中所获得解循环路径的优劣有关，更新规则会让短路经较优的解上对应的信息素量逐步增加。

为了研究算法模型对算法性能的影响，将算法中其他的参数固定(蚁群数量=30，迭代次数=100次，ρ=0.5，α=1.0，β=10，Q=10)，针对att48数据集，对不同的算法模型各进行10次测试，结果如下表2：

表2 算法模型对算法性能的影响

根据实验结果可见，当蚂蚁数量小于30时，随着蚁群数量的不断增大，100次迭代后得到的平均路径长度不断优化，而当蚂蚁数量超过30时，蚂蚁数量对于结果的影响开始变得不再那么明显。耗时方面，每增加5个蚂蚁，耗时约增加4秒。因而，针对att48数据集，考虑效果与耗时，可将蚂蚁数目设为30个，即约0.6倍的城市数目。

2.4信息素残留系数(ρ)对算法性能的影响

在蚁群算法中，人工蚂蚁是具有记忆功能的，随着时间的推移，以前留下的信息素将逐步消逝。当信息素残留系数(ρ)过大时，以前被搜索过的解被选择的可能性过大，会影响到算法的随机性能和全局搜索能力。反之，当ρ过小时，虽然可以提高算法的随机性能和全局搜索能力，但又会使算法的收敛速度降低。因此，选择一个合适的信息素残留系数是十分必要的。

为了研究信息素残留系数对算法性能的影响，将算法中其他的参数固定(采用Ant-quantity模型，蚁群数量=30，迭代次数=100次，α=1.0，β=10，Q=10)，针对att48数据集，对不同的信息素残留系数各进行10次测试，结果如下表3：

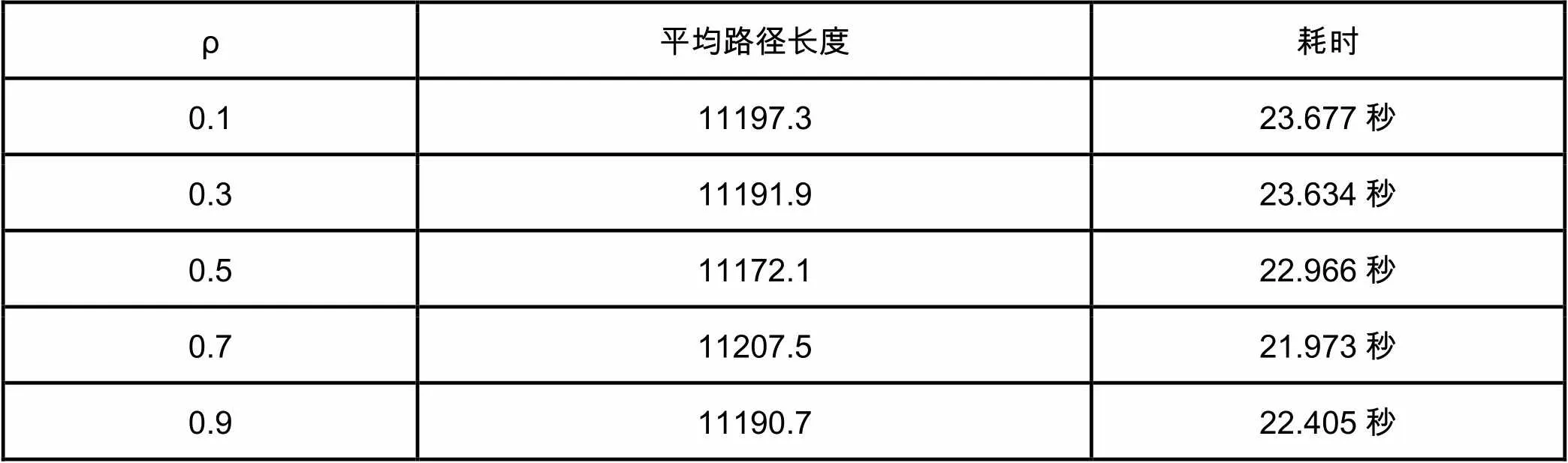
表3 ρ对算法性能的影响

根据实验结果可见，针对att48数据集，信息素残留系数为0.5时，平均路径长度最小，而五组不同的ρ值对于耗时几乎不存在影响。因而，本文认为，信息素残留系数设为0.5较优，原因在于，每只蚂蚁需要忘记过去获得的一部分经验，避免蚂蚁过早的收敛到一个局部最优解，使得蚂蚁可以更好的探索新引入的全局信息。

2.5信息素重要程度系数(α)对算法性能的影响

信息素重要程度系数(α)的大小反映了在蚁群路径搜索中的随机性因素作用的强度，其值越大，蚂蚁选择以前走过的路径的可能性也越大，搜索的随机性减弱。因而，α值过大会使蚁群的搜索过早陷于局部最优。

为了研究信息素重要程度系数对算法性能的影响，将算法中其他的参数固定(采用Ant-quantity模型，蚁群数量=30，迭代次数=100次，ρ=0.5，β=10，Q=10)，针对att48数据集，对不同的信息素重要程度系数各进行10次测试，结果如下表4：

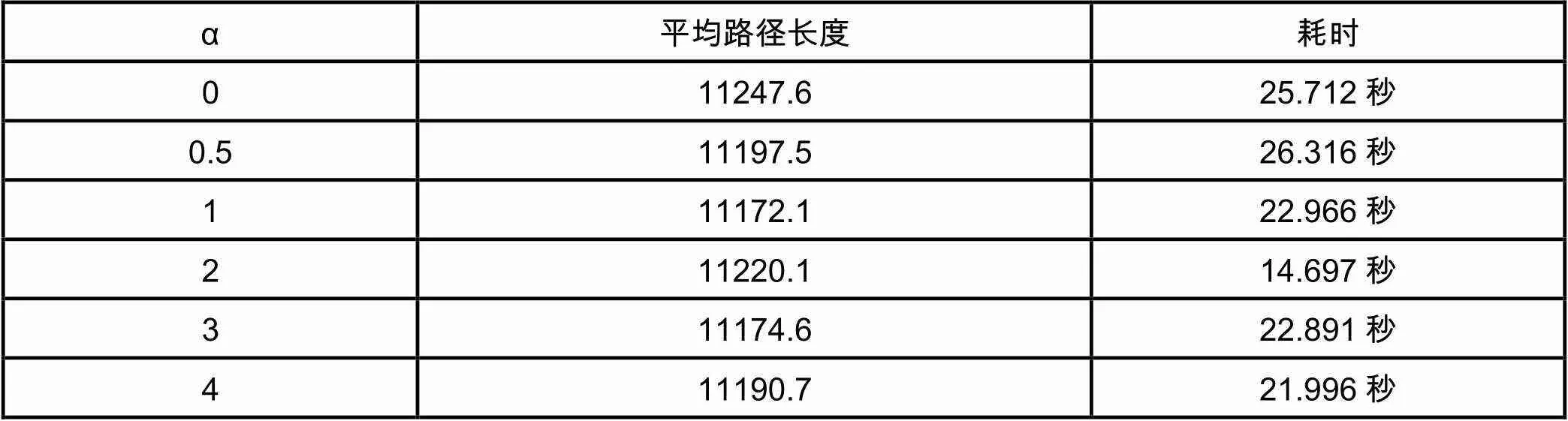
表4 α对算法性能的影响

根据实验结果可见，针对att48数据集，信息素重要程度系数为1.0时，平均路径长度最小，而六组不同的α值对于耗时的影响不大。因而，本文认为，信息素重要程度系数设为1.0左右较优。原因在于，α过小时，而且算法易陷入局部最优解；而α过大时，局部最优路径上的正反馈作用很强，算法会出现过早收敛，同样对结果存在负影响。

2.6两城市间距离重要程度系数(β)对算法性能的影响

两城市间距离(β)的大小反映了在蚁群路径搜索中确定性因素作用的强度，其值越大，蚂蚁在某个局部点上选择局部最短路径的可能性越大，尽管搜索的收敛速度加快，但蚁群在最优路径的搜索过程中的随机性减弱，易于陷入局部最优。

为了研究两城市间距离重要程度系数对算法性能的影响，将算法中其他的参数固定(采用Ant-quantity模型，蚁群数量=30，迭代次数=100次，ρ=0.5，α=1.0，Q=10)，针对att48数据集，对不同的两城市间距离重要程度系数各进行10次测试，结果如下表5：

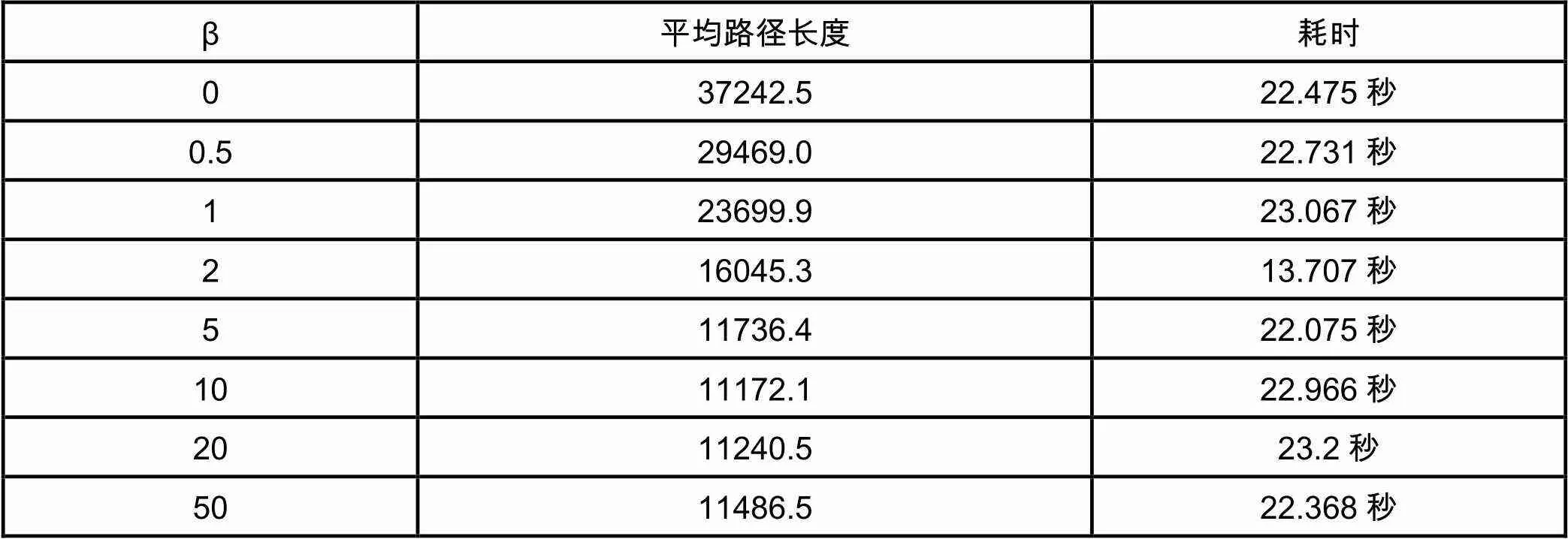
表5 β对算法性能的影响

根据实验结果可见，针对att48数据集，在两城市间距离重要程度系数小于10时，随着β值的增长，效果迅速优化；而当β值超过10后，β值对于结果开始呈现负影响。因而，本文认为，两城市间距离重要程度系数设为10左右较优，既保证了一定的随机性，又保证了路径搜索中确定性因素作用的强度。

2.7蚂蚁循环一周在经过的路径上释放的信息素总量(Q)对算法性能的影响

蚂蚁循环一周在经过的路径上释放的信息素总量(Q)越大，则在蚂蚁所走过的路径上的信息素的累积加快，因而可以加强蚁群搜索时的正反馈性能，有助于算法的快速收敛。但一般认为，蚁群算法参数中对算法性能起主要作用是α、β及ρ三个参数，而总信息量对算法性能的影响有赖于以上三个参数的配置，对算法性能的影响不大。

为了研究Q值对算法性能的影响，将算法中其他的参数固定(采用Ant-quantity模型，蚁群数量=30，迭代次数=100次，ρ=0.5，α=1.0，β=10)，针对att48数据集，对不同的Q值各进行10次测试，结果如下：

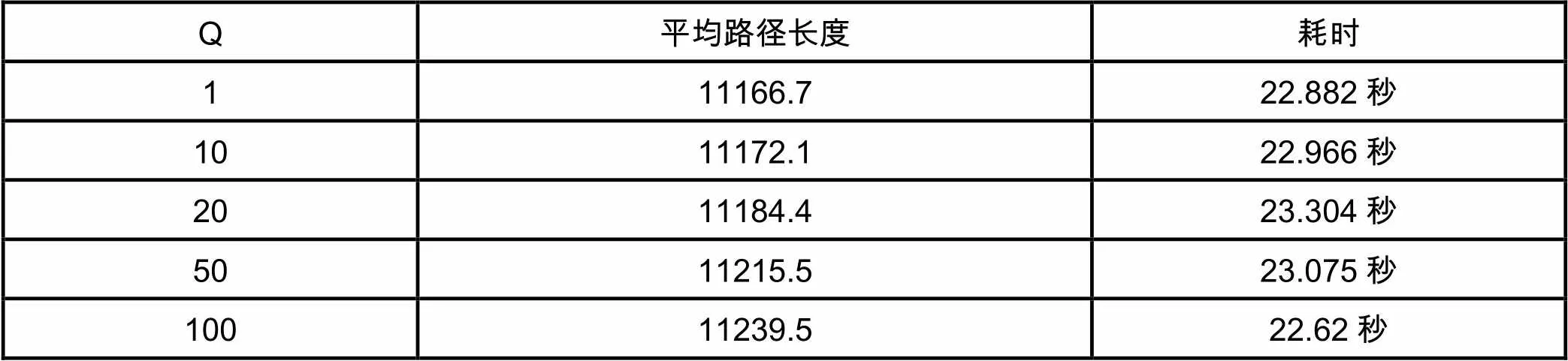
表6 Q对算法性能的影响

根据实验结果可见，针对att48数据集，Q值在1~20之间时，对结果的影响的影响十分微弱，直到Q值为50时，结果才有较为明显的劣化。而在耗时方面，Q值几乎对耗时不存在任何影响。因而在实际使用时，Q值可以在1~20之间灵活的选取。

3 结束语

在基本蚁群算法的实际使用中，参数对算法效果有十分显著的影响，若选择不当，则容易暴露出其存在的但搜索时间长、易陷于局部最优解的缺点。本文通过一系列的实验，研究了在att48数据集下参数的设置对蚁群算法性能的影响。实验结果表明，基本蚁群算法中参数的最优设置为：蚁群数量约为0.6倍城市数量，信息素重要程度系数(α)约为1.0左右，两城市间距离重要程度系数(β)约为10左右，信息素残留系数(ρ)约为0.5左右，蚂蚁循环一周在经过的路径上释放的信息素总量(Q)可以在1~20之间灵活的选取。算法模型方面，若Ant-cycle模型的效果较其他两者优势较大，则应选择Ant-cycle模型；若效果优势不大，则可考虑选择耗时较短的其他两种模型。

[1]丛明煜，王丽萍.现代启发式算法理论研究[J].高技术通讯, 2003.

[2]熊伟平，曾碧卿.几种仿生优化算法的比较研究[J].计算机技术与发展，2010.

[3]冯玉蓉.模拟退火算法的研究及其应用[D].昆明理工大学，2005.

[4]梁军.粒子群算法在最优化问题中的研究[D].广西师范大学，2008.

[5]王银年.遗传算法的研究与应用[D].江南大学，2009.

[6]邹采荣，张潇丹，赵力.混合蛙跳算法综述[J].信息化研究，2012.

[7]吴庆洪，张颖，马宗民.蚁群算法综述[J].微计算机信息， 2011.

[8]吴华锋，陈信强，毛奇凰等.基于自然选择策略的蚁群算法求解TSP问题[J].通信学报，2013.

[9]Wei Xianmin. Parameters Analysis for Basic Ant Colony Optimization Algorithm in TSP[J]. International Journal of u-and e-Services, Science and Technology, Vol.7, No.4 (2014).

[10]杨剑峰.蚁群算法及其应用研究[D].浙江大学，2007.

[11]刘乃文，王奎峰.蚁群优化算法及其应用[J].山东师范大学学报(自然科学版)，2006.

[12]刘利强，戴运桃，王丽华.蚁群算法参数优化[J].计算机工程，2008.