基于改进相似度计算方法的协同过滤算法
2018-05-10孟俊才李存志
孟俊才 李存志

摘要
在协同过滤算法中,相似度度量方法是其核心。传统的相似性度量方法主要关注了共同评分项之间的相似度,却未考虑其评分标准和共同评分数量对相似性的影响。本文提出了平均分惩罚机制和共同评分项惩罚机制,对缺失的项目评分进行计算。实验表明,本文所提方法能较好的提高推荐的准确性和稳定性。
【关键词】协同过滤 Pearson相似度 共同评分项目
1引言
随着近年来信息技术的迅猛发展,为人们的工作、学习和生活提供了很大的便利。然而,面对各种形态的信息,人们无法及时准确的找到满足自己需求的信息,目前主流的已有很多高效的推荐算法,包括基于内容的推荐、基于协同过滤的推荐、基于关联规则的推荐等。协同过滤算法以其更优异的性能被更多的人使用,其核心是根据历史行为在用户群找出相似的用户,对自己未浏览过的项目进行预测。但是项目数量的增大,会导致用户的数据急剧稀疏,会很大程度的影响推荐的准确性。对于协同过滤算法的缺陷,已有很多学者做出了不懈的努力。
计算相似度时,皮尔森相似度或改进后的余弦相似度都是以平均分作为不用的用户的评价标准,会受到数据稀疏的影响,可能某个用户只选择了少量的自己不感兴趣的商品,就会导致整体评分偏低,此时就不能用平均分去衡量一个用户的评分标准。并且,不同用户之间共同评分项数量的多少也会影响到整体的准确性,如果两个用户之间对于不同项目的评分公有项很少,但相似度很高,而共同评分项很多,相似性偏低,显然是不合理的。故综上两个问题,本文提出了平均分惩罚机制和共同评分项惩罚机制,来削弱平均分差距大和共同评分项少的对相似性度量的影响,进而优化数据稀疏问题。由实验表明,此方法可以更好的度量不同用户之间的相似度,提高了系统整体的推荐准确性,也使得系统更加稳定性。
2协同过滤算法的缺陷及改进
2.1传统协同过滤算法
传统的协同过滤推荐算法是根据用户的评分矩阵,寻找和目标用户的前k个最相近的样本,从而预测出目标用户为评分的项目的近似评分,进行最终推荐。常用相似性度量方法有以下三种。
余弦相似度:用户u对项目j评分作为向量u,用户v对j项目评分作为向量v,不同用户之间的相似度用cos(u,v)表示,既两个向量之间夹角的cos值。
修正的余弦相似度:余弦相似度没有考虑评分标准问题,會导致评分标准高的只能和评分标准高的相似性较强,显然不合理,故引出修正的余弦相似性,用用户u对于项目j的评分Ruj减去其所有评分过的项目的均值,能更好的产生推荐结果。
相关相似性:此方法考虑了每个项目的评分对于用户的衡量标准问题,故在每个项目上都减去了平均分,使得计算更为精准。其计算方法和修正的余弦相似度一致。本文采用此方法。
2.2协同过滤算法的缺陷及改进
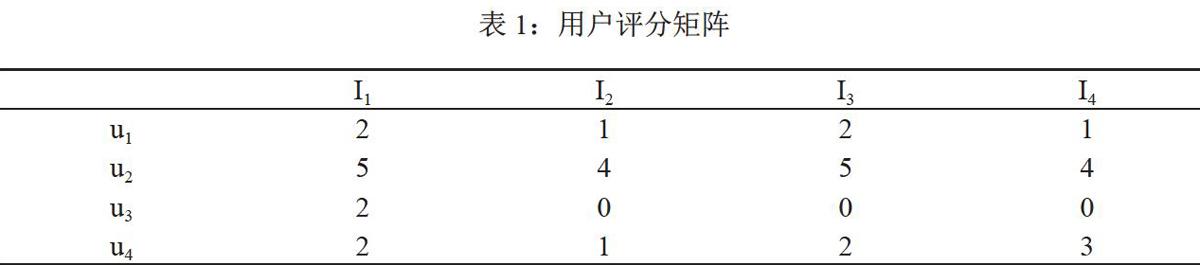
评分标准问题:由于数据的稀疏,会出现两个用户的衡量标准相同,一个用户看到的都是自己感兴趣的,另一个用户看到的都是不感兴趣的,如表1所示,用户u1的评分都处于3分以下,表示都不太感兴趣,用户u2的评分都处于3分以上,表示兴趣度很高,虽然算法中都减去了各自的平均分,但相似度为l,是不合理的,需要改进。
共同评分项占比问题:同样由于数据的极度稀疏,评分矩阵中不同用户公有的评价过的项目极少,会因此导致虽然共同评分项极少,但相似度极高。如表1所示,O表示未评价,用户u1和用户u3共同评分项只有项目I1,且评分相同,相似度值为l。而用户Ul和用户U4共同评分项为I1、I2和I4,因在项目I1上的评分不同,导致其相似度低于ul和u2的相似度,也是不合理的。
评分标准惩罚机制:提出了两个用户对于同一个项目评分的差值比d-|ruj-rvj|/N,用户u和v对项目j的评分分别为rnj和rvj,N表示系统所允许的最大评分,本文最大评分为5。用户u和用户v对于同一项目的评分差与系统支持最大评分比可以很好的度量用户间评分的差异,对平均分不同而方差近似的用户进行了约束,从而能够更准确的衡量其相似性。
低共同评分项惩罚机制:前文讲到低共同评分项会使得部分用户的贡献度低而对于评分预测占很大的权重。不同用户间所评分电影的交集越多时,说明两个用户的兴趣方向一致,从而可以用共同评分项占比去衡量两个人的相似关系,可以用Tanimoto系数表示,T(u,v)=(∑ui∩vi)/(∑(ui ∪vi),用户u和用户v交集与其并集的商即为其共同评分项占比,避免了用户间共同评分项目少,而评分近似导致相似度很高的情况。
针对评分标准不同和低共同评分项对用户间相似性的影响,上文提出了不同的解决方案,结合不同用户间的评分差占比和Tanimoto系数,本文对Tanimoto系数进行了修正,如公式所示,修正后的Tanimoto能够更好的抑制用户间平分差值大和共同评分项少的问题,使得计算相似性更加准确。
将传统的相关相似性度量公式与修正后的Tanimoto相结合,去重新计算用户相似矩阵,SIM既本文最终使用的计算方法:SIM-sim+simp∞。
3实验结果及分析
实验数据采用MovieLens数据集,该数据为943名用户对1682部电影的100000条评分,评分范围为1-5的整数,0表示未评分。随机选取80%作为训练集,20%作为测试集。
平均绝对误差:用预测出的数据与测试集的误差衡量算法的准确性,MAE=l/n∑|ru,j - ruJ|,ru.j,ru,J分别表示实际评分和预测评分,MAE为绝对误差的均值,数值越小表示准确率越高。
均方根误差:它是观测值与真值偏差的平方与观测次数n比值的平方根。1/n∑(ru,j-ru,J)2ru,j表示实际评分,ru,J表示预测评分,n表示预测出的数据集合,计算结果RMSE为均方根误差,数值越小表示偏差越小,推荐精度越高。
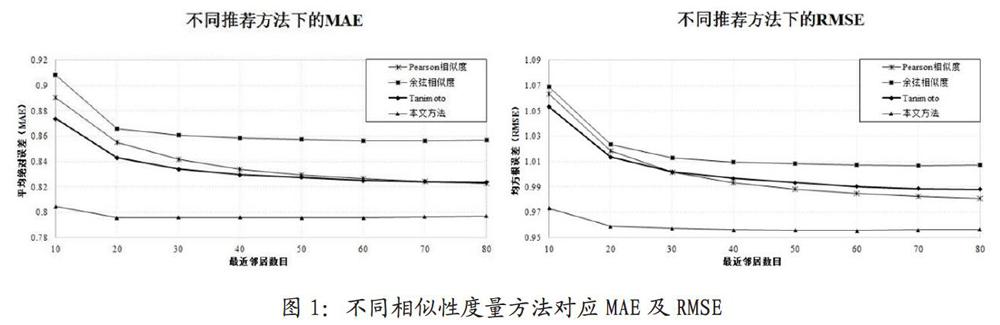
本文改进后的算法对数据中缺失的数据进行预测,将之与测试集中的数据进行平均绝对误差和均方根误差计算,用于衡量预测的准确性。根据最近邻k值得不同,将传统的协同过滤算法与本文改进后的协同过滤算法进行对比。如图1所示。
将传统协同过滤算法中的Tanimoto相似性、余弦相似性以及相关相似性与本文的算法进行对比。由图1中可看出本文算法较传统相似性算法准确度有较高的提升,本文算法在k值为10时,比传统相似性算法MAE值降低约10%,RMSE值降低约8.5%,且在k为20时趋于收敛,故有很好的稳定性,无需提供较多的邻居集合即可得到较为准确的预测结果,有助于提供系统的效率也有助于缓解数据稀疏带来的负面影响。
参考文献
[1]陈雅茜,音乐推荐系统及相关技术研究[J].计算机工程与应用,2012,48 (18):9—16.
[2]杨武,唐瑞,卢玲,基于内容的推荐与协同过滤融合的新闻推荐方法[J].计算机应用,2016,36 (02):414-418.
[3]Kaleli C. An entropy-based neighborselection approach for collaborativefiltering[J]. Knowledge-BasedSystems, 2014, 56 (C): 273-280.
[4]何明,刘伟世,张江.支持推荐非空率的关联规则推荐算法[J].通信学报,2017 (10):18-25.
[5]陈曦,成韵姿.一种优化组合相似度的协同过滤推荐算法[J].计算机工程与科学,2017, 39 (01):180-187.
