热应力对恐龙化石风化损坏的影响研究

张尚坤,于学峰，贾超,杜圣贤,宋香锁，陈诚，刘凤臣，陈军，陈文芳

(1.山东省地质科学研究院，国土资源部金矿成矿过程与资源利用重点实验室，山东省金属矿产成矿地质过程与资源利用重点实验室，山东 济南 250013;2.山东大学土建与水利学院，山东 济南 250013)

1 概述

热应力是引起岩石破坏的一个重要因素，由热应力引起的岩石破裂称为热破裂。根据热传导理论，对于同样的物体，在相同加热条件下，如果初始条件和边界条件不同，即加热方式不同，由于热传导在时间和空间上的迟滞效应，在物体表面和内部的温度分布将存在较大的差异，这将导致物体中应力的集中和分布的差异[1-3]。在研究陶瓷材料的热性能过程中研究人员发现热冲击在物体表面产生的热应力要大于均匀加热产生的热应力。Moon V等人[4-6]在研究蒸汽压力对沉积岩石热破裂的影响实验中，得到了与此相同的结论。恐龙化石热破坏主要是在太阳光照的条件下，由于受热不均匀及日照长久往复循环作用，使得化石表面可能产生裂缝，从而加速了恐龙化石风化损害。

引起热应力的基本条件是在约束下有温度的变化。产生热应力的约束条件大致可以归纳为：外部变形的约束，相互变形的约束，内部各区域之间变形的约束。就岩石而言，各矿物之间的物理力学性质有较大的差异，在温度变化时，由于内部各区域热变形的不协调而产生热应力；当有地温梯度存在时，即使没有外部约束，但由于相互变形的约束，也将产生较大的热应力。由这些因素引起的热应力很容易导致岩石中弱介质的破坏，从而改变岩体力学性质和力学行为[7-8]。恐龙化石挖掘过程中，大量的化石暴露地表，很多化石的一部分出露地表，一部分仍埋藏于地表下[9-18]。由于空气和地表下岩石介质不同，受热条件不同，比热容和热传导特性各异，造成化石暴露在空气中的部分与埋藏在地表下的部分产生温度差，受热膨胀不均匀而产生破坏应力。

恐龙骨骼化石是被埋葬的恐龙骨骼经过自然地质作用，经钙化、碳化、硅化、矿化形成的岩石，而保留了原骨骼的形状和结构。矿物成分包含多种矿物颗粒，在受热作用下，由于这些矿物颗粒在热力学上表现出的差异(热膨胀各向异性、热膨胀不均匀性等)使得化石内部结构发生相应的变化，当这些变化超过化石自身的内部结合力限度时，就会在化石内部产生微裂缝，从而引起化石物性参数(如孔隙度、渗透率等)的变化，加速恐龙化石的风化。

该试验主要针对日照产生在恐龙化石件各处不同温度差异分布情况下，恐龙化石试件的物理力学受力变形特性进行研究。通过有限差分软件FLAC3D进行数值模拟[19-23]，揭示日光辐射造成的恐龙化石温度差异分布对化石风化的影响。

2 研究的理论基础

通常热力耦合方程可以描述为：

(1)

σij,ii+Fbi=ρiii

(2)

εij=(ui,j+uj,i)/2

(3)

σij=λεmmδij+2Gεij-βΔΤδij

(4)

β=(3λ+2G)α

(5)

式中：σij和εij为应力和应变项；Fbi为体力；β为热应力系数；ΔΤ为温度改变量，即ΔΤ=T-T0；δij为Kronecker函数；Q，λ，G，α，k，ρ和c分别为热生成率、拉梅常数、剪切模量、热膨胀系数、热传导系数、密度和比热。

严格地说，这些方程是相互关联的，应该一起求解。然而，对大多数的工程问题来说，应变对温度分布的影响比较小，且惯性变量项也非常小，即式(1)中的和式(2)中的可以忽略不计。这样一来，温度场的计算就纯属热传导范围，应力场的计算中包含了热应力项。所以在计算时就可以先计算出温度场，然后再计算由温度和外荷载共同引起的应力和变形等。

基于上述分析，该数值模型中有关热力耦合的求解就可以分两步进行，即先根据温度条件计算出模型中的温度场，然后根据力学条件求解应力场并进行相应的破坏处理。即每个单元满足如下的热传导方程和应力场方程。

热传导方程为：

(6)

Τ(p,t)|p∈S1=φ(p,t) (边界条件为S1)

(7)

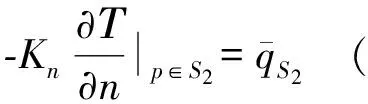
(8)

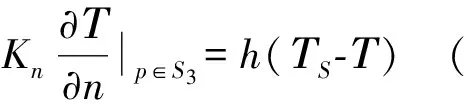
(9)

Τ|t=t0=Τ(p,t0) (在t0时刻)

(10)

应力-应变场方程为：

σij,j+Fbi=0 (平衡方程)

(11)

εij=(ui,j+uj,i)/2 (几何方程)

(12)

σij=λεkkδi,j+2Gεij-βΔΤδij(物理方程)

(13)

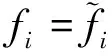
(14)

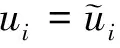
(15)

β=(3λ+2G)α(边界条件为S1)

(16)

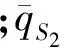
岩石材料在外载作用下，当应力达到其所受力强度极限后，其应力会随着变形的增加而降低,这种现象通常被称之为“应变软化”。由于应变软化的影响，结构变形稳定发展到一定程度之后，会突然失去变形的稳定性，导致结构的动态破坏失效。另一方面，破裂的岩石仍具有一定的残余承载力。针对岩石应变软化破坏特性，FLAC3D提供了一种具有应变软化/硬化特性的本构模型—Strain-Hardening/ Softening Mohr-Coulomb Model[20,24]，基于摩尔库伦的破坏准则，破坏屈服后摩擦角、粘聚力、剪胀角、抗拉强度等能以一定的规律递减，最终达到一个稳定的强度值。该构模型如图1所示；屈服后粘聚力、摩擦角变化如图2所示。

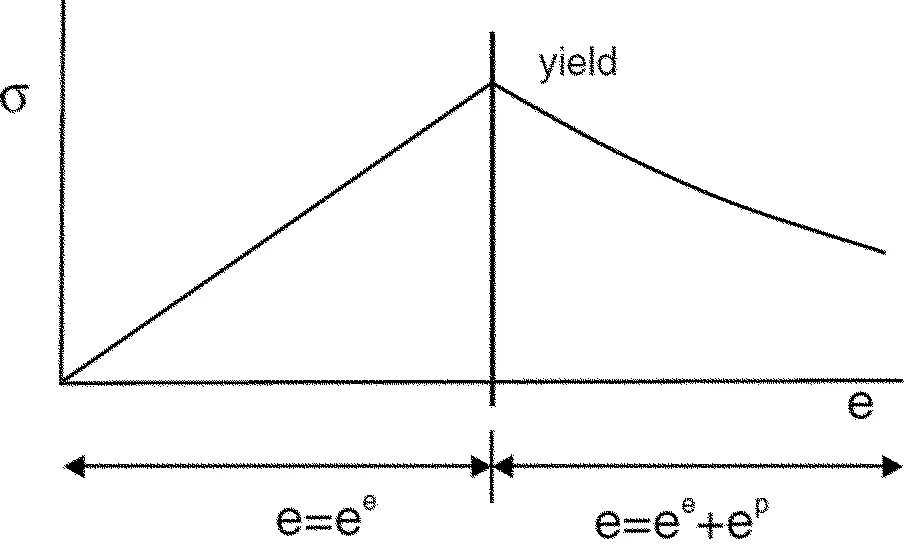
图1 应变软本构模型应力应变曲线

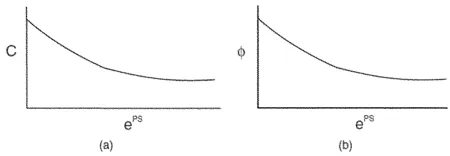
图2 屈服后粘聚力(a)、摩擦角(b)的变化曲线示意图

3 模拟试验条件的设定

模拟试验的主要目的是研究不同温度场下，恐龙化石试件单轴压缩变形特性[25]。为了方便研究，采用Strain-Hardening/Softening Mohr-Coulomb Model本构模型，将恐龙化石试件设定为直径50mm，长100mm的圆柱体试块，模型共计6144个单元，6897个节点(图3)。

图3 模拟计算模型

由于地表介质不同，吸收的阳光辐射也不同，导致日照作用下地表温度与气温存在较大差异，实测显示：一般情况下，岩石的地表温度要大大高于气温，在日照直射的区域，当空气温度为40℃时，岩石地表最高温度可以达到50℃～60℃。而埋藏在地下1m范围的物体，其最低温度可以只有十几摄氏度。因此，开挖出露的恐龙化石在日照辐射作用下，化石暴露在空气中的部分与埋藏在土层中的部分存在较大温差，化石内部存在温度梯度场，在温度不均匀的热膨胀作用下，会使得试块中产生易导致化石破坏的温度拉应力,岩石的热物理性质如表1所示。根据恐龙化石赋存情况，设计采用7种不同的工况进行对比试验研究，具体情况如表2所示。

表1 岩石热物理性质

表2 恐龙化石地下与地表部分温度比较

4 试验模拟结果与分析

(1)温度应力分布场

不同温度梯度场作用下，圆柱体试件的温度分布情况和其产生的温度应力分布情况如图4—图10所示，对比温度应力可以发现：随着温差逐渐增大，圆柱体试块的上半部分的四周表面出现拉应力，在温度差异值大于30℃后变得比较明显。而在试件内部却为压应力，应力分布不均匀容易导致块体的表面的开裂。

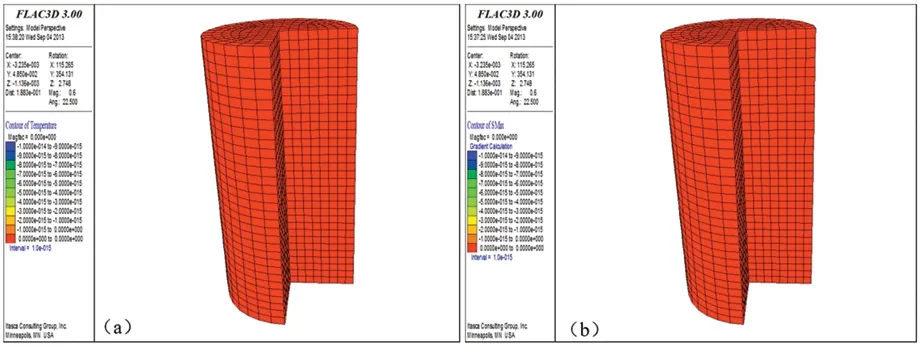
(a)—温度场分布；(b)—温度拉应力分布图4 工况1(温差0℃)温度场与温度拉应力分布云图

(a)—温度场分布；(b)—温度拉应力分布图5 工况2(温差10℃)温度场与温度拉应力分布云图

(a)—温度场分布；(b)—温度拉应力分布图6 工况3(温差20℃)温度场与温度拉应力分布云图

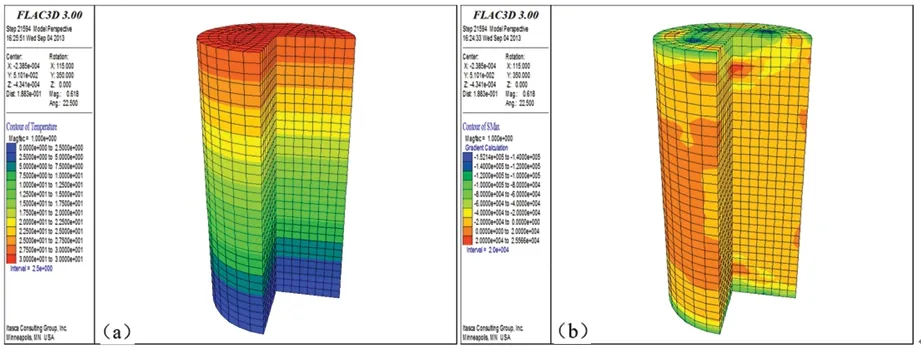
(a)—温度场分布；(b)—温度拉应力分布图7 工况4(温差30℃)温度场与温度拉应力分布云图

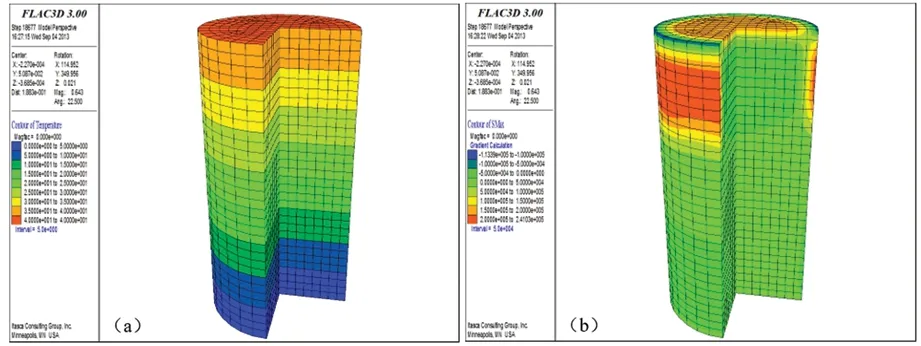
(a)—温度场分布；(b)—温度拉应力分布图8 工况5(温差40℃)温度场与温度拉应力分布云图

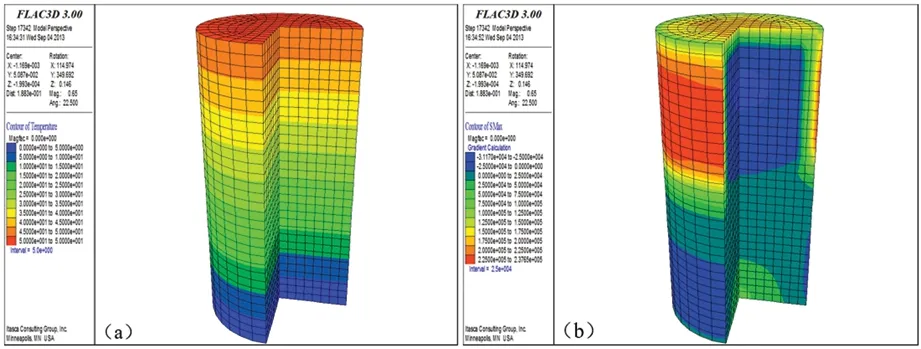
(a)—温度场分布；(b)—温度拉应力分布图9 工况6(温差50℃)温度场与温度拉应力分布云图

(a)—温度场分布；(b)—温度拉应力分布图10 工况7(温差60℃)温度场与温度拉应力分布云图

(2)不同工况单轴压缩破坏结果

对不同温度应力分布的试件进行单轴压缩模拟试验，试验结果如图11—图17所示，试验结果显示随温度梯度增长塑性破坏区域变化不大，但是塑性流动区域，即破坏后变形滑动的区域，逐渐从中部扩展到试件的两端表面。这个过程在温度差大于30℃以后，表现得较为明显。

(3)应力应变曲线变化分析

在对既有温度应力的恐龙化石单轴加载试验过程中，在模型上设置了4个应力监测关键点(图18)，用于观察在试验加载过程中，关键点的应力随模型的轴向应变的变化关系，以及加载应力随轴向应变的变化关系(图19—图25)。

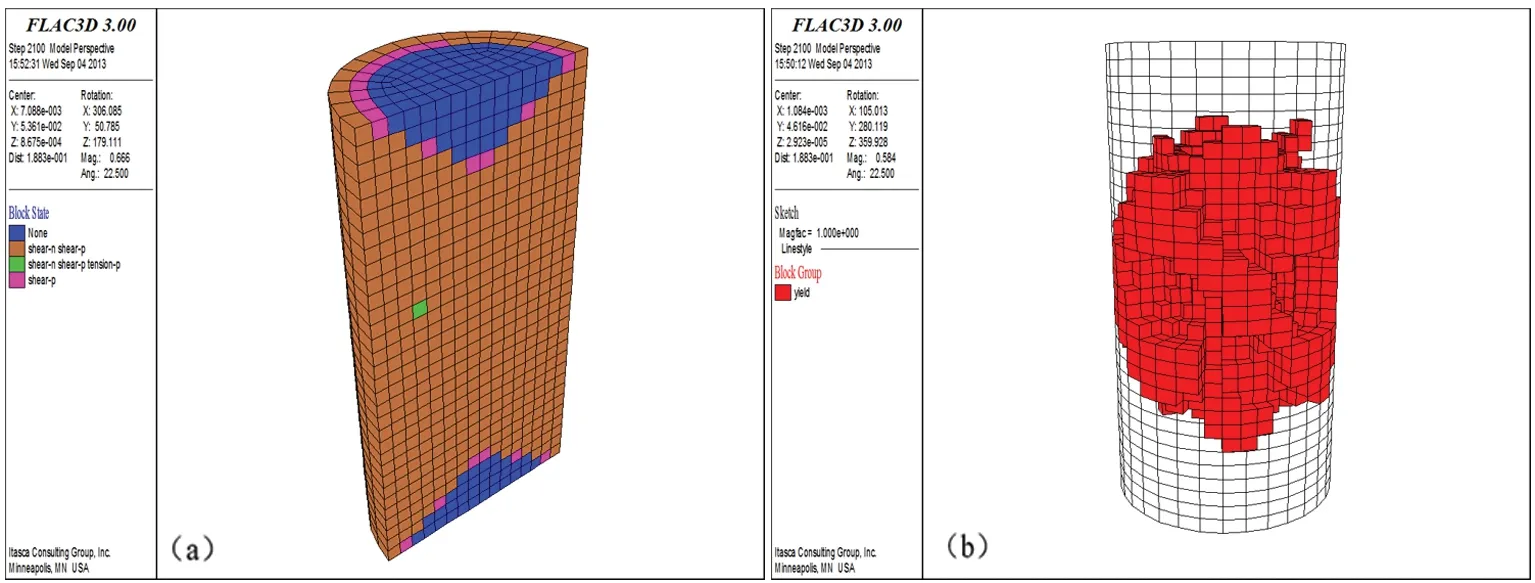
(a)—塑性破坏区；(b)—剪切流动变形区图11 工况1(温差0℃)试件单轴压缩剪切破坏单元分布

(a)—塑性破坏区；(b)—剪切流动变形区图12 工况2(温差10℃)试件单轴压缩剪切破坏单元分布

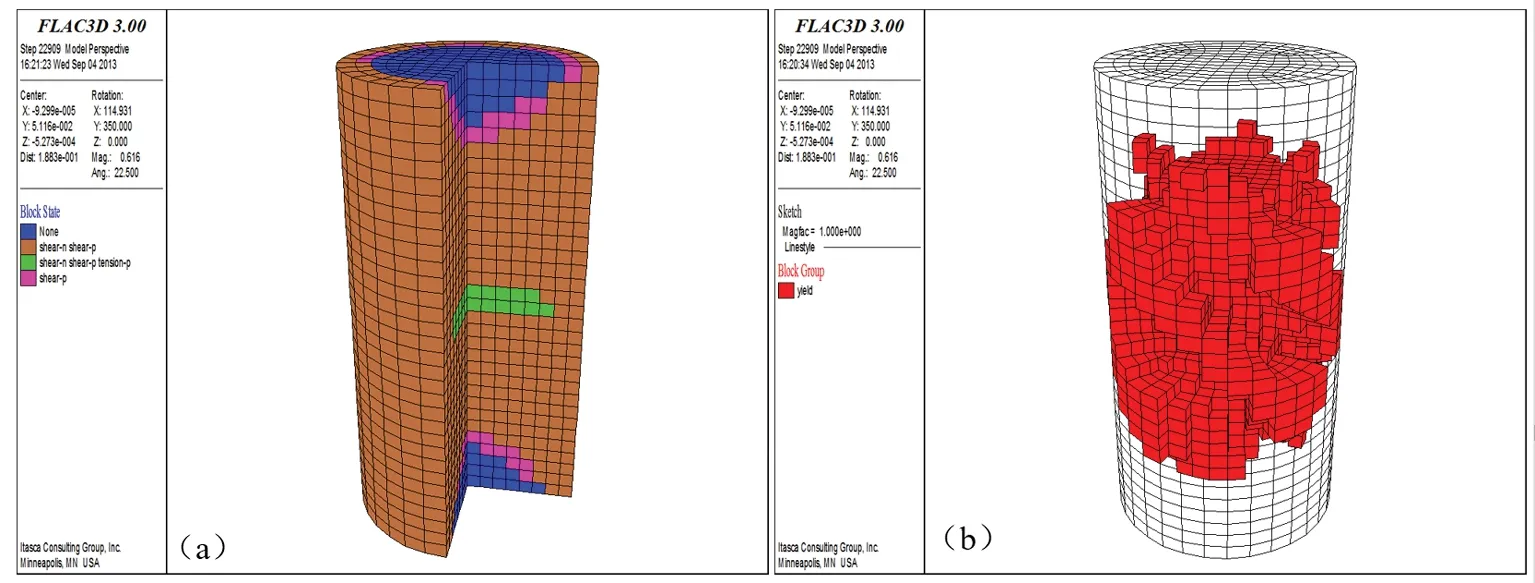
(a)—塑性破坏区；(b)—剪切流动变形区图13 工况3(温差20℃)试件单轴压缩剪切破坏单元分布

(a)—塑性破坏区；(b)—剪切流动变形区图14 工况4(温差30℃)试件单轴压缩剪切破坏单元分布

(a)—塑性破坏区；(b)—剪切流动变形区图15 工况5(温差40℃)试件单轴压缩剪切破坏单元分布

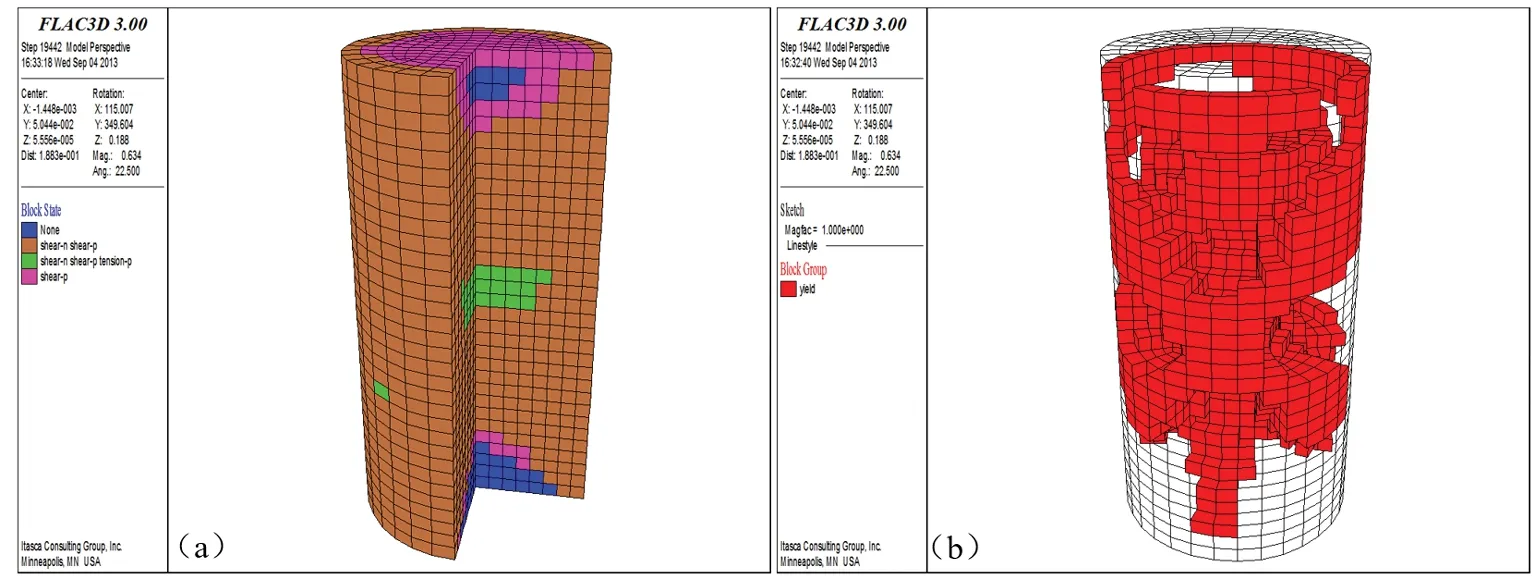
(a)—塑性破坏区；(b)—剪切流动变形区图16 工况6(温差50℃)试件单轴压缩剪切破坏单元分布

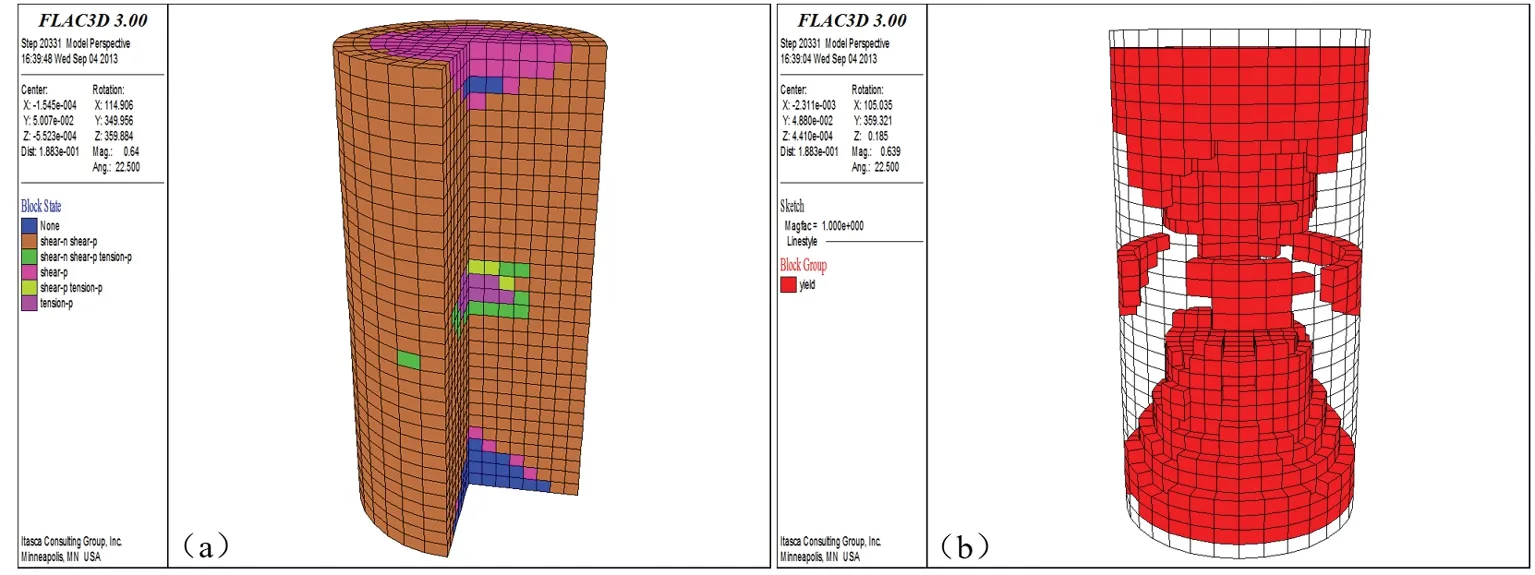
(a)—塑性破坏区；(b)—剪切流动变形区图17 工况7(温差60℃)试件单轴压缩剪切破坏单元分布

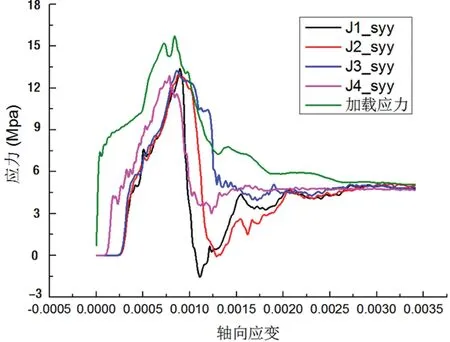
图20 工况2监测点应力应变曲线

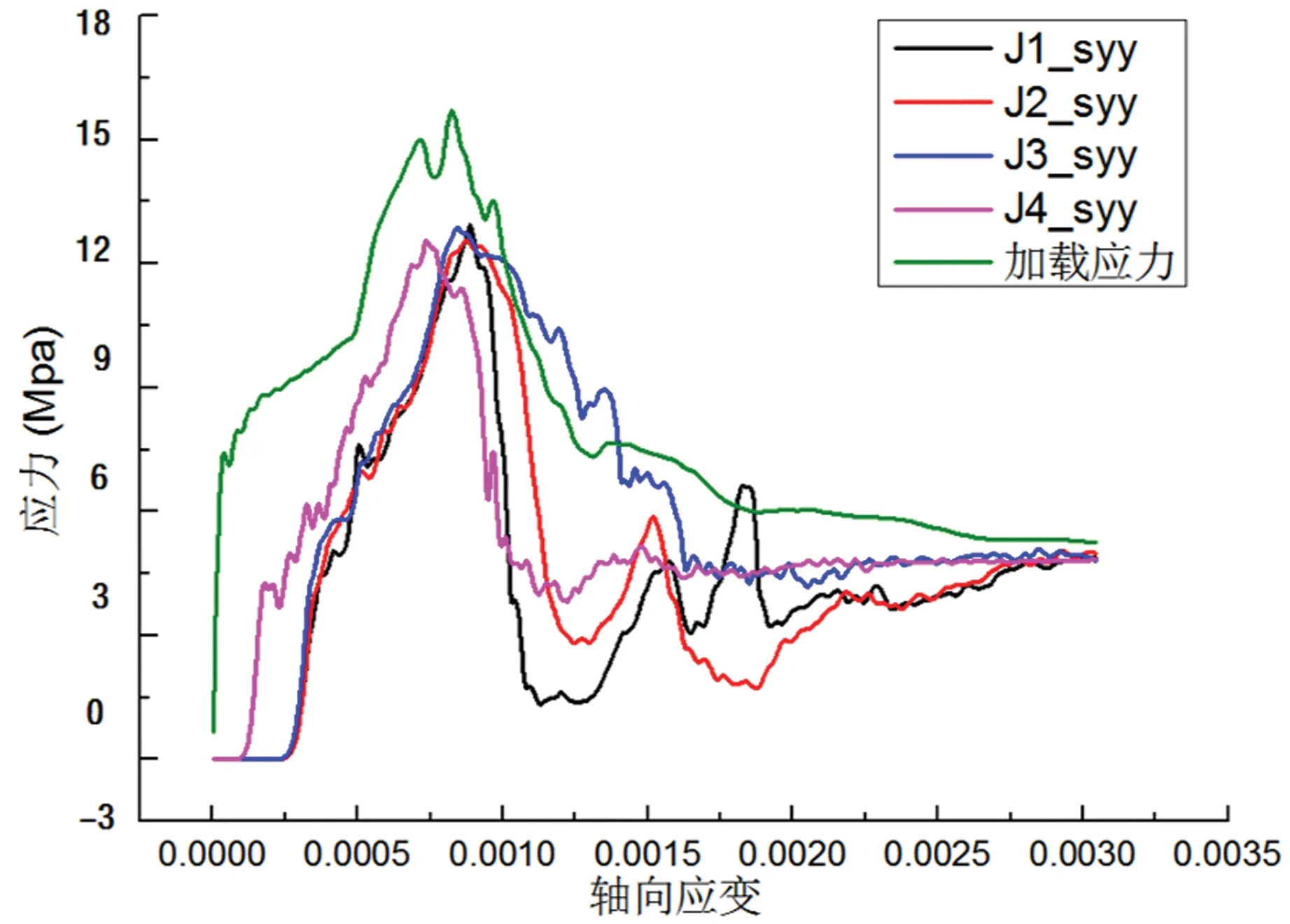
图21 工况3监测点应力应变曲线

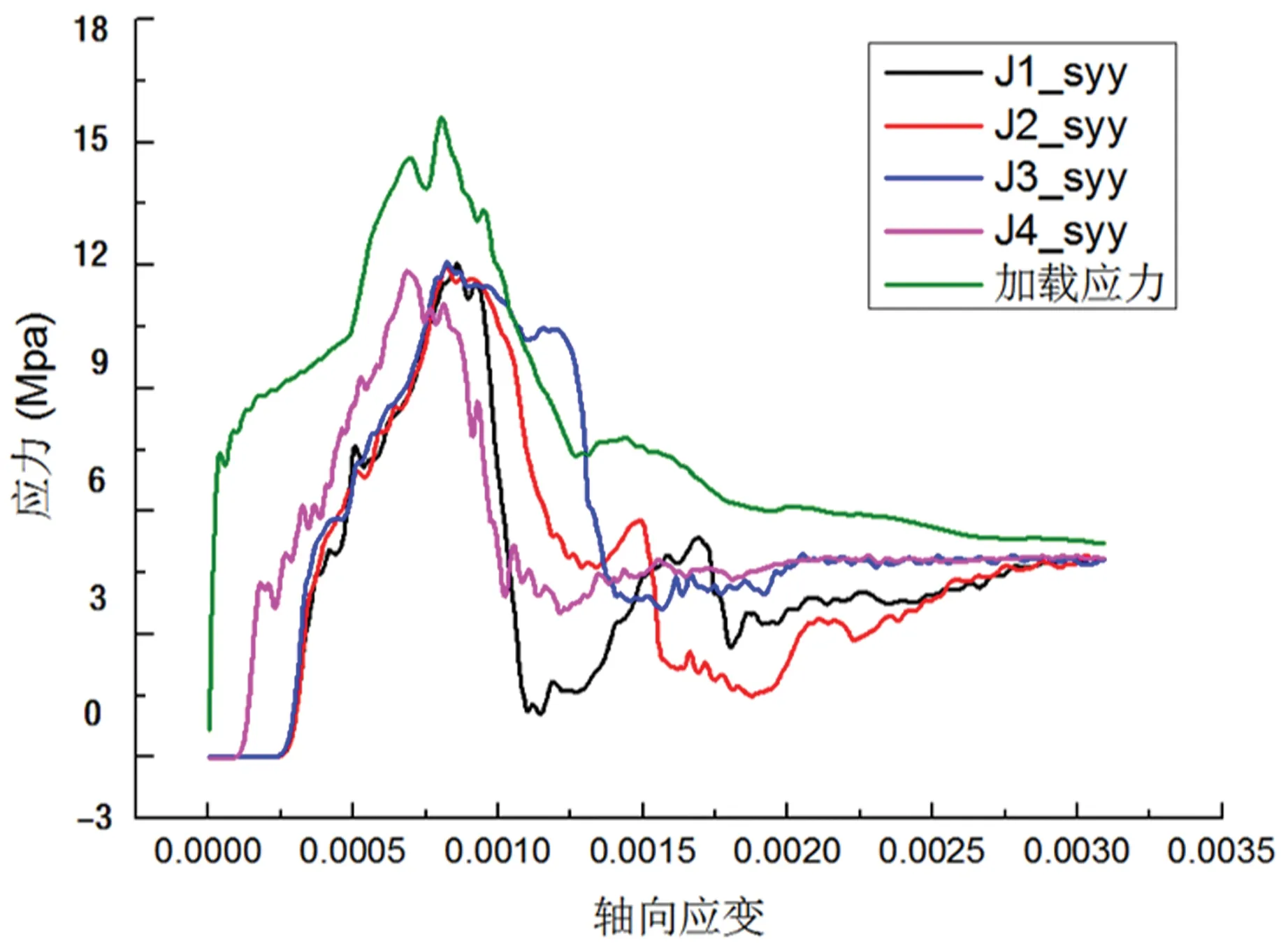
图22 工况4监测点应力应变曲线

从以上实验结果可以看出，温度应力场的存在对化石应力峰值抗压强度的影响不大，但是对化石应力峰后强度有较为显著的影响。对比温度差异较小的工况1、工况2与工况3,4,5,6,7的应力应变曲线可知，温度应力场较小时，监测点应力峰后应力应变曲线较为平滑一致，而温度应力场较大工况下，监测点应力峰后的应力应变曲线会有较大的起伏波动，据此分析，波动是由于单元体产生较大塑性流动破坏造成的，说明塑性流动区随温度梯度增大而扩展。

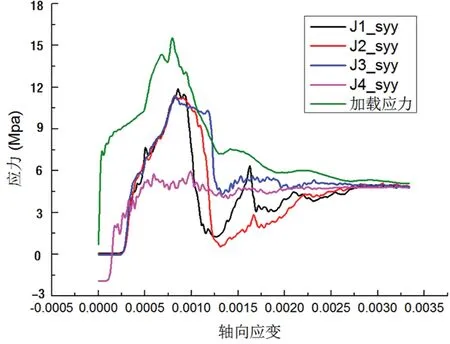
图23 工况5监测点应力应变曲线

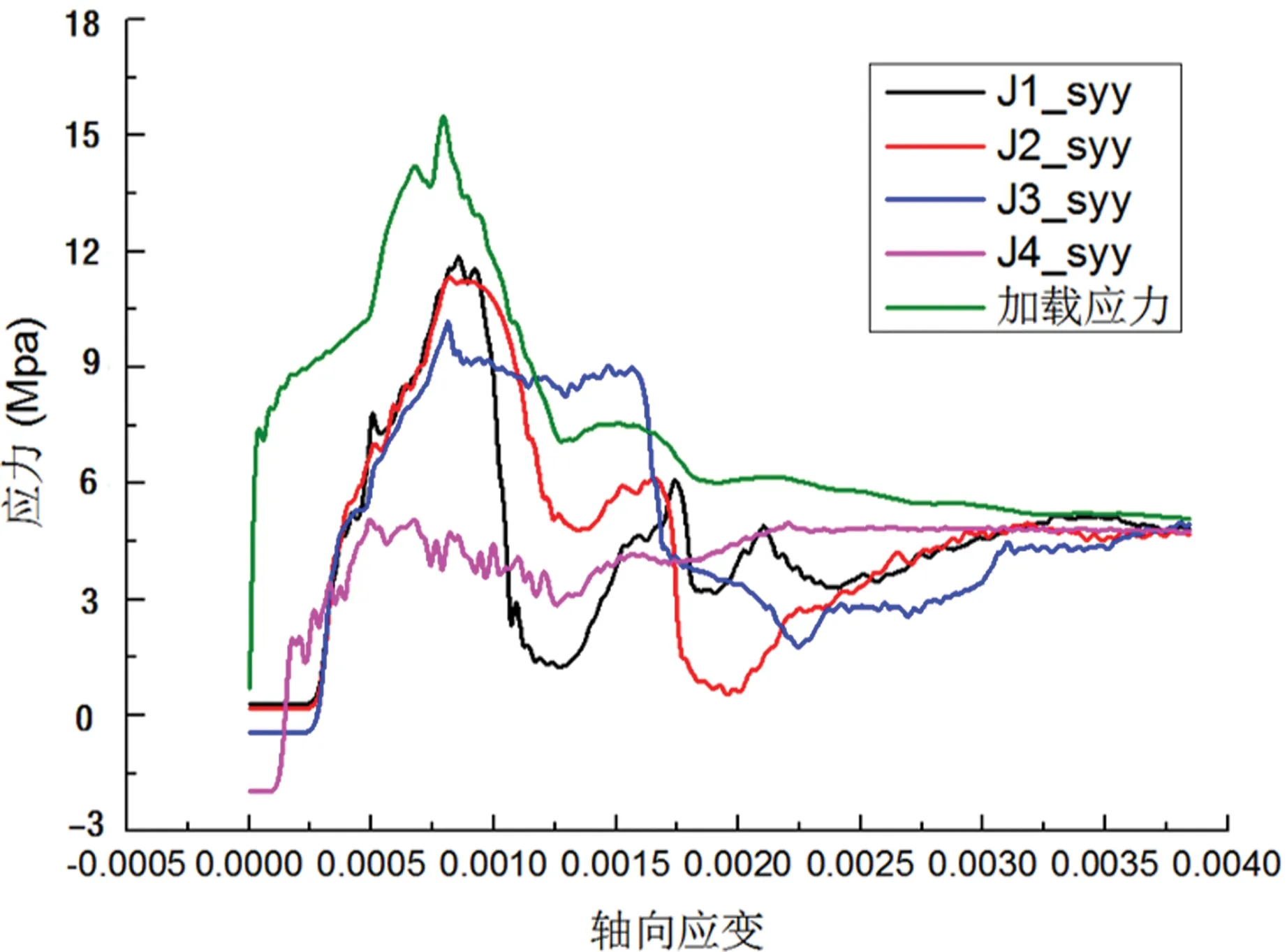
图24 工况6监测点应力应变曲线

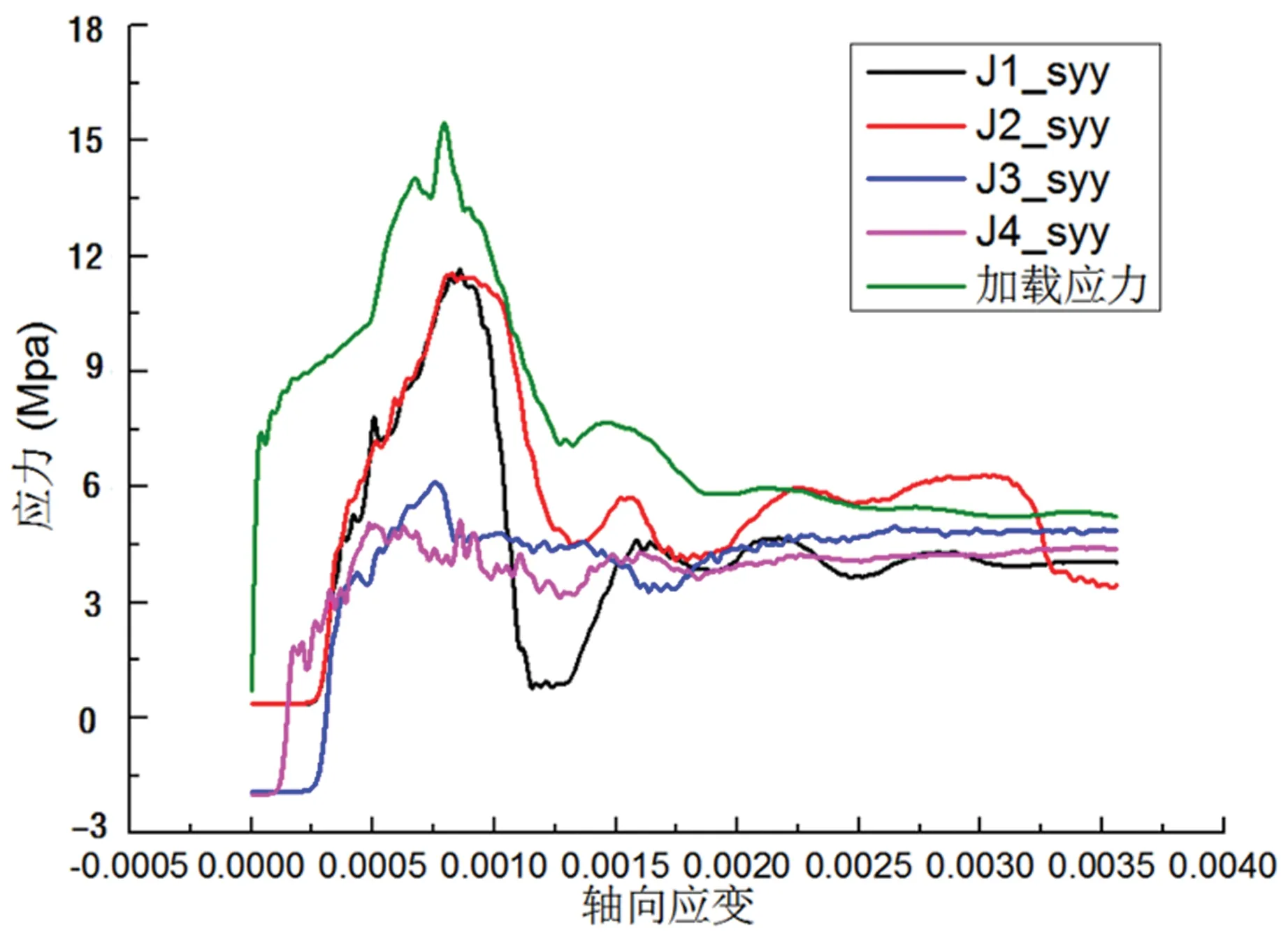
图25 工况7监测点应力应变曲线

5 结论

(1)热应力是引起化石体破裂风化的一个重要原因，化石作为一种特殊岩石其矿物成分、结构构造等存在很大的差别。在受热作用下，化石内部发生热开裂现象，导致化石内部结构发生变化。

(2)温度梯度差异对化石的影响，主要表现在温度的热膨胀作用下，化石的表面出现拉应力区，由于化石本身是脆性材料，若温度不断循环变化，在化石表面就会形成长久往复的拉压循环应力，极易造成化石表面产生微小裂缝，并使裂缝不断扩张，形成空气进出通道，加速化石风化破坏。

(3)温度分布不均匀，往往还会加重一定初始地应力场中化石的受力状况。埋藏在地层中的化石是在一定的地应力场中生成的，当部分被发掘暴露后，其本身有一定的应力释放，内部的应力分布是不均匀的。因此，在受外界温度影响下，温度热应力的作用，很可能造成应力分布情况的恶化，使得局部应力过大，造成化石开裂。

(4)在化石发现挖掘中，暴露后的化石风化破坏明显加快，通过实验证明埋藏在地下的化石部分与暴露在空气中的化石部分的温度差异，是造成化石内部热应力分布不均匀的重要原因。另外，在受外部热源(如太阳辐射)作用下，产生在化石表面与内部温度梯度分布，也是造成化石应力分布不均匀的原因，因此化石保存要尽量放在恒温环境下，避免化石温度往复变化。

参考文献：

[1] 张渊,张贤,赵阳升.砂岩的热破裂过程[J].地球物理学报,2005,48(3):656-659.

[2] 秦本东,何军,谌伦建.石灰岩和砂岩高温力学特性的试验研究[J].地质力学学报,2009,15(3):253-261.

[3] 杨俊杰,黄思静,张文正，等.表生和埋藏成岩作用的温压条件下不同组成碳酸盐岩溶解过程的实验模拟[J].沉积学报,1995,13(4):49-54.

[4] Moon V,Jajawardane J.Geomechanical and geochemical changes during early stages of weathering of Karamu Basalt,New Zealand[J].Engineering Geology,2004,74:57-72.

[5] White A F,Bullen T D.Differential rates of feldspar weathering in granitic regoliths[J]．Geochimica et Cosmochimica，2001,65(6):847-869.

[6] Matsukara Y,Hashizume K,Oguchi C T．Effect of microstructure and weathering on the strength anisotropy of porous rhyolite[J].Engineering Geology,2002,62:39-47.

[7] 肖洪天,周维垣.脆性岩石变形与破坏的细观力学模型研究[J].岩石力学与工程学报，2001,20(2):151-155.

[8] 刘元高,周维垣,赵吉东，等.裂隙岩体损伤局部化破坏分岔模型及其应用[J].力学学报,2003,35(4):411-418.

[9] 杜圣贤，于学峰，宋香锁，等.山东省古生物化石保护规划研究[M].北京：地质出版社，2017：1-84.

[10] 王申娜，陈树清，张艳霞，等．山东“恐龙涧”创造三个“世界之最”[J]．中国地理杂志，2010(6):88-93.

[11] 陈树清．山东诸城恐龙化石发掘新成果[J]．化石,2010(1):9-11．

[12] 赵喜进，李敦景，韩岗，等．山东的巨大诸城龙[J]．地球学报，2007,2(4):111-122．

[13] 季燕南．巨型山东龙的系统分类、生活习性与生态环境研究[J]．地学前缘，2010,17(1):378-385.

[14] 韩振玉,王经,王秀静,等.莱阳恐龙谷地层古生物现状与保护建议[J].山东国土资源,2015,31(10):36-39．

[15] 夏文杰,李秀华．恐龙埋藏环境及岩相古地理特征[M]．成都:四川科学技术出版社，1988．80-82．

[16] 柳永清,旷红伟，姬书安，等．鲁东诸城地区晚白垩世恐龙集群埋葬地沉积相与埋葬学初步研究[J]．地质论评，2010.56(4):4457-4468.

[17] 杨群，王怡林,李朝真，等．原子光谱和X射线衍射研究禄丰恐龙化石与围岩特征[J]．光谱学与光谱分析，2005，25(2)：299-301.

[18] 杜圣贤,张尚坤,于学峰,等.恐龙化石风化效应的TM耦合分析研究[J].山东国土资源,2015,31(10):65-70.

[19] 刘波,韩彦辉.FLAC原理实例与应用指南[M].北京:人民交通出版社，2004:79-90.

[20] 陈育民,徐鼎平.FLAC/FLAC3D基础与工程实例[M].北京：中国水利水电出版社,2009：1-20.

[21] Fairhurst C,Cook N G W.The phenomenon of rock splitting parallel to the direction of maximum compression in the neighborhood of a surface crack[A].In:Proc.First Congress International Society for Rocks Mechanics[C].Lisbon:Lisbon Press,1966:15-65.

[22] Kemeny J,Cook N G W.Effective moduli no-linear deformation and strength of a cracked elastic solid[J].Int. J .Rock Mechanics. Min. Sci. & Geomech. Abstr.,1986,23(2):107-118.

[23] Kemeny J,Cook N G W.Micromechanics of deformation in rock[A].In:Toughening Mechanism in Quasi-Brittle Materials[C].Netherlands:Kluwer Academic Publishers,1991:62-78.

[24] 孙卫军,周维垣.裂隙岩体弹塑性—损伤本构模型[J].岩石力学与工程学报，1990,9(2):108-119.

[25] 傅晏,刘新荣,张永兴，等．水岩相互作用对砂岩单轴强度的影响研究[J]．水文地质工程地质，2009(6)：54-58．