水平循环荷载作用下群桩与软粘土相互作用离心模型试验研究

张宇亭

(交通运输部天津水运工程科学研究所 港口水工建筑技术国家工程实验室，天津 300456)

近年来，海洋灾害性天气频发，风浪作用下，码头等结构物破坏的情况时有发生。由于受到波浪、船舶等长期的循环加载作用，使得结构物地基中的群桩与饱和软粘土相互之间的作用发生变化，引起地基承载力下降，不均匀沉降发生，导致桩基断裂、上部承台倾斜或裂缝，造成事故。饱和软粘土的软化、弱化现象及其带来的危害逐渐被认知，因此开展外力作用下桩基与软土之间的相互作用方面的研究，是对消除工程隐患，实现水工构筑物安全运行的重要保证，也对我国沿海沿江的水运工程发展具有重要的意义。

1-a 西澳大学鼓式离心机 1-b 天科院臂式离心机图1 土工离心机Fig.1 Geotechnical centrifuges

土工离心机是通过高速旋转，在模型箱中实现高倍离心加速度场，从而开展缩尺模型试验的土工设备。对于岩土工程专业的相关研究来说，放置在高倍重力加速度场中的土工模型具有比尺缩小、变形相似、应力应变和破坏机理相同的特点。通过开展土工离心模拟试验，同时具有时间和空间两方面的优势[1]。土工离心机通常有两种：鼓式离心机和臂式离心机，如图1所示。

在土工离心模拟试验中，对于原型尺寸，任意深度处的土体应力(σ)可由以下式表示

σ=ρgZ

(1)

式中:ρ为土体的密度；g为重力加速度；Z为土体的深度。土工离心机可以提供一个人造高重力场，在模型土工建筑物中再现原型的性状。例如，当人造重力场的加速度是重力加速的N倍时，土体的尺寸便可以缩小N倍，如式(2)所示。

σ=ρ(Ng)(Z/N)

(2)

可见，离心模型试验中的土体应力与原型尺寸是一致的。对于多数岩土工程结构，特别是大尺度的结构物，其受力状态和变形特性很大程度上取决于本身所受到的重力。因此，采用离心模型试验研究大型结构物的变形特性具有明显的优势。

本文以软土地基上的高桩码头工程为背景，重点研究波浪、船舶等水平循环荷载作用下，群桩基础与软粘土相互作用的特性。通过土工离心机模型试验，分析水平循环荷载作用下，桩基位移、土体变形的特点。

1 离心模型试验方案

根据实际工程地质参数及码头桩基尺寸，本次离心试验比尺选定为1:40，即在40倍重力加速度场开展试验。所用的模型箱尺寸为长1 245 mm，宽350 mm，按照离心模拟试验的比尺关系，相当于实际尺寸为长49.8 m，宽14 m。表1中列出了土工离心模拟试验和实际情况下各物理量的相似比关系[3]。

1.1 模型设计

图2为群桩离心模拟试验的立面布置图，基于现场勘察资料，地基由粘土层和砂土层组成，因此模型土层分两层：上部为粘土层，下部为砂土层。按照表1提供的相似比关系，离心模型试验的上部粘土层厚度为250 mm，对应到原型尺寸为10 m；下部砂层的厚度为150 mm，对应到原型尺寸为6 m。模型桩刺入到砂土层中，桩尖的刺入深度为31.5 mm，对应到原型尺寸为1.5 m。水位控制在粘土层以上283 mm处，对应到实际水深为11.32 m。在桩顶处，施加水平循环加载—卸载。2×2的群桩布置在模型箱的中间。为了观测水平循环荷载作用下桩周土体的变形，2×2的群桩模型安装在模型箱的透明玻璃面侧。沿模型的纵向和横向，桩间距分别为175 mm和87.5 mm。

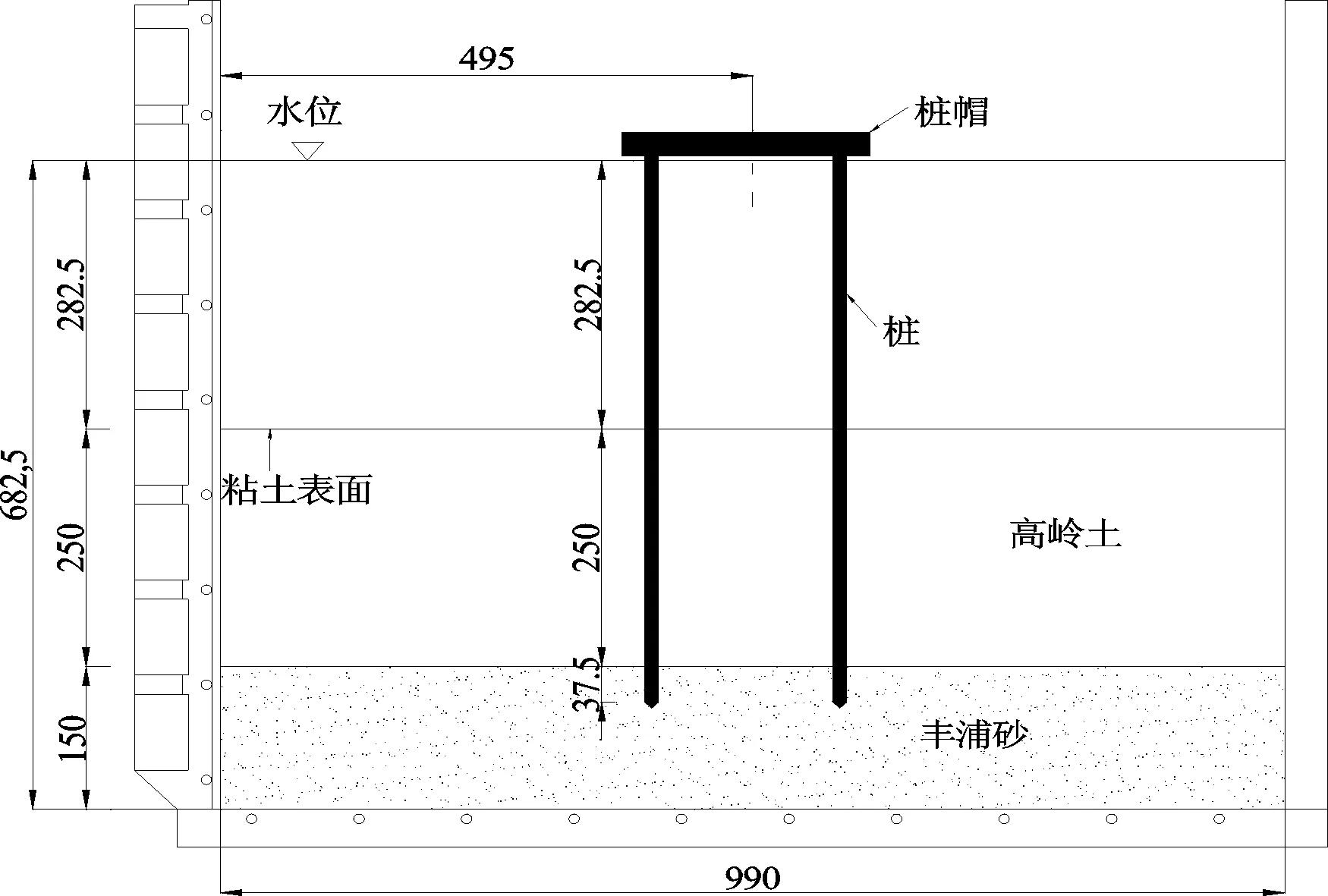
图2 群桩离心模型试验立面布置图(单位：mm)Fig.2 Layout of model section

表1离心模型试验常用的相似比

Tab.1 Scales of centrifuge model test

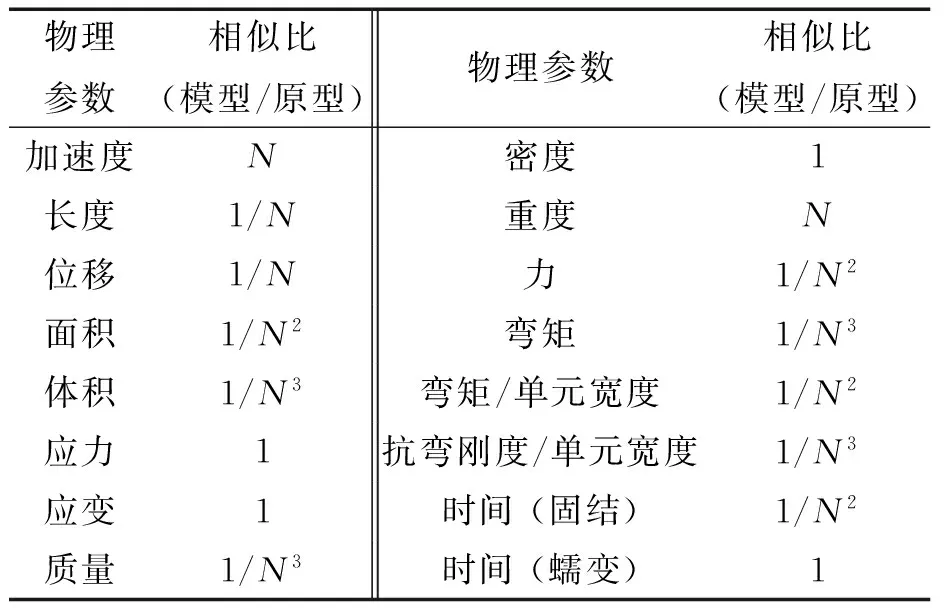
物理参数相似比(模型/原型)物理参数相似比(模型/原型)加速度N密度1长度1/N重度N位移1/N力1/N2面积1/N2弯矩1/N3体积1/N3弯矩/单元宽度1/N2应力1抗弯刚度/单元宽度1/N3应变1时间(固结)1/N2质量1/N3时间(蠕变)1

1.2 模型桩

图3 离心模型 图4 离心模型试验采用试验所用群桩 的微型应变片Fig.3 Model pile Fig.4 Micro strain gauge

图3、图4为离心模型试验采用的模型桩及应变片。模型桩的材质为铝合金，其杨氏模量为70 GPa，横截面为规则的空心正方形，边长为12.7 mm，对应实际尺寸为0.51 m；模型桩长和壁厚分别为560 mm和1.58 mm，对应到实际尺寸为22.4 m和63.2 mm。在40倍的重力加速度下(40 g)，此模型桩的抗弯刚度为2.65×102 MNm2。当混凝土的杨氏模量取35 GPa，此模型桩相当于实际工程中截面积为550 mm的实心混凝土桩。

本次试验重点研究水平循环加载—卸载作用下桩基的水平位移和弯矩。因此，对于埋设在土层中的模型桩，在桩身按照微型应变片测量水平循环荷载作用下的桩身弯矩。沿桩身方向，布置了9级应变片，应变片的间距为35 mm，对应到原型尺寸为1.4 m。

1.3 模型布设安装

图5 循环加卸载系统 图6 群桩离心模型布置图 Fig.5 Loading system Fig.6 A typical centrifuge model package

图5为群桩的水平循环荷载加载系统，主要包括一个液压千斤顶、一个伸长杆、一个应力传感器和一个差动位移传感器。差动位移传感器安装在桩帽上，一旦桩顶产生任何水平位移就会被差动位移传感器捕捉。图6为群桩离心试验模型布置图。离心模型试验研究水平循环荷载对预制桩的影响，因此，在布置模型桩之前，需要提前在制备好高岭土和丰浦砂层中钻出与模型桩截面尺寸一致的规则矩形孔。为了防止安装过程中桩身产生倾斜，事先在模型箱上方安装特制的铝合金桁架，然后将模型桩在垂直状态下缓慢插入预先钻好的孔中。安装完模型桩后，在桩顶安装水平循环加载卸载装置。

2 试验步骤

首先，安装完模型桩、加载系统和传感器后，模型箱被吊装到离心机吊篮中。其次，通过水管将模型箱和离心机排水和供水系统连接起来，确保离心模型试验过程中水箱的水位不发生变化。然后，逐步增加离心机的重力加速度场至40g，让粘土层在40倍的重力加速度下充分固结。当差动位移传感器测得地表沉降达到最终沉降的95%以上时(即固结度大于95%)，最后，在桩顶施加水平加载和卸载，并通过离心机的数据采集系统记录每一个加载—卸载循环引起的桩顶水平位移和桩身弯矩。

3 水平循环荷载作用下群桩变形特性分析

水平循环荷载作用下单桩和群桩的变形特性主要包括桩顶位移、桩身弯矩与循环次数间的关系，水平循环荷载的大小对桩顶位移和桩身弯矩的影响规律及其超孔隙水压力沿深度的变化规律。除特别说明，离心模型试验中的实测数据均已转化到原型尺寸对应的结果。

3.1 桩顶位移

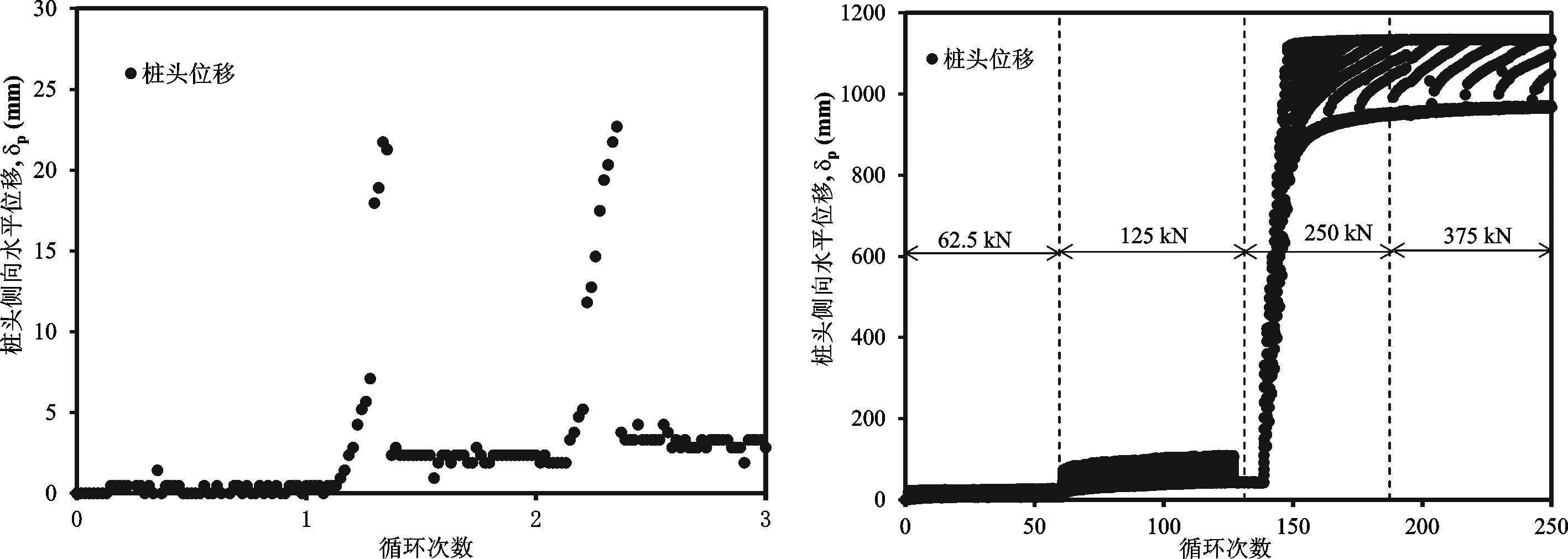
7-a 前两个循环 7-b 所有循环图7 加载卸载循环过程中典型的桩顶位移变化图Fig.7 Typical lateral pile head movements during cyclic loading and unloading

图7-a为循环加载卸载作用下，桩顶的典型位移变化图。在前两组加载循环试验中，施加的最大荷载值和加载周期分别相当于实际情况下的62.5 kN和1 d。在加载过程中，桩顶的水平位移显著增加；当水平荷载降低时，位移值随之减小。每个加载和卸载周期完毕后，群桩都不能回到初始位置。这表明：加载—卸载循环使得桩周围的土体发生了残余变形，而且残余变形随着加载荷载的增加而增大。这是因为在加载—卸载循环过程中，桩周围土体产生了累积的塑性变形。

图7-b显示了桩顶水平位移和循环加载次数之间的变化关系。当加载值小于125 kN时，桩顶的最大位移为106 mm。当加载值达到250 kN时，最大的桩顶位移增大到1 134 mm。这说明桩顶水平荷载从125 kN增加到250 kN时，桩周土体引起了明显的塑性变形。然而，当继续增大水平荷载值至375 kN时，桩顶的最大和残余位移值的变化却微乎其微。这说明在上一级荷载值加载过程中，桩周围土体的塑性变形量已经接近达到极限值。每一级荷载下，桩顶位移先快速增加，随后逐步达到一个稳定值，这说明桩顶的位移以递减的速率随着加载次数的增加而增加。随着加载—卸载次数的增加，浅层土体与桩身便会脱开，脱开位置逐渐向深处移动。深部土体尤其是砂土的强度明显是大于浅层土的，桩身位移便会受到更大的阻力。因此，桩顶位移的增量随着加载—卸载次数的增加而逐步降低。

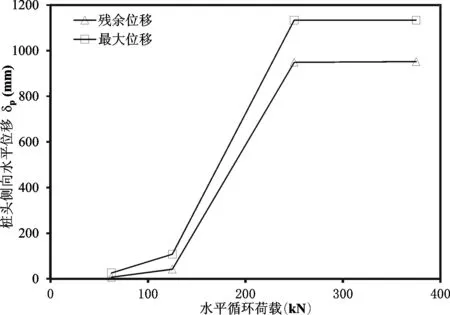
图8 水平循环荷载与桩顶水平位移之间的关系曲线Fig.8 Relationship between lateral pile head movement and applied cyclic load

3.2 桩顶水平位移同水平循环加载值之间的关系

图8显示了桩顶水平位移同水平循环加载值之间的变化关系。水平向施加的荷载值分别为62.5 kN，125 kN，250 kN和375 kN。加载过程中，桩顶最大水平位移值从26.0 mm增加到1 134 mm，桩顶残余的水平位移值从7.6 mm增加到952 mm。实测结果明确显示出桩顶的最大和残余位移值随着施加荷载值的增大而快速增大。当施加的水平循环荷载值从62.5 kN增大到375 kN时，桩顶的残余位移值与最大位移值的比值从0.30增大到0.84。这意味着当桩顶施加的水平循环荷载值较小时(62.5 kN和125 kN)，大部分的桩顶水平位移都得以恢复。这是因为施加荷载值较小时，桩对土体仅产生较小的塑性变形，大部分弹性变形得以恢复。

3.3 循环加载过程中典型的桩基弯曲变形

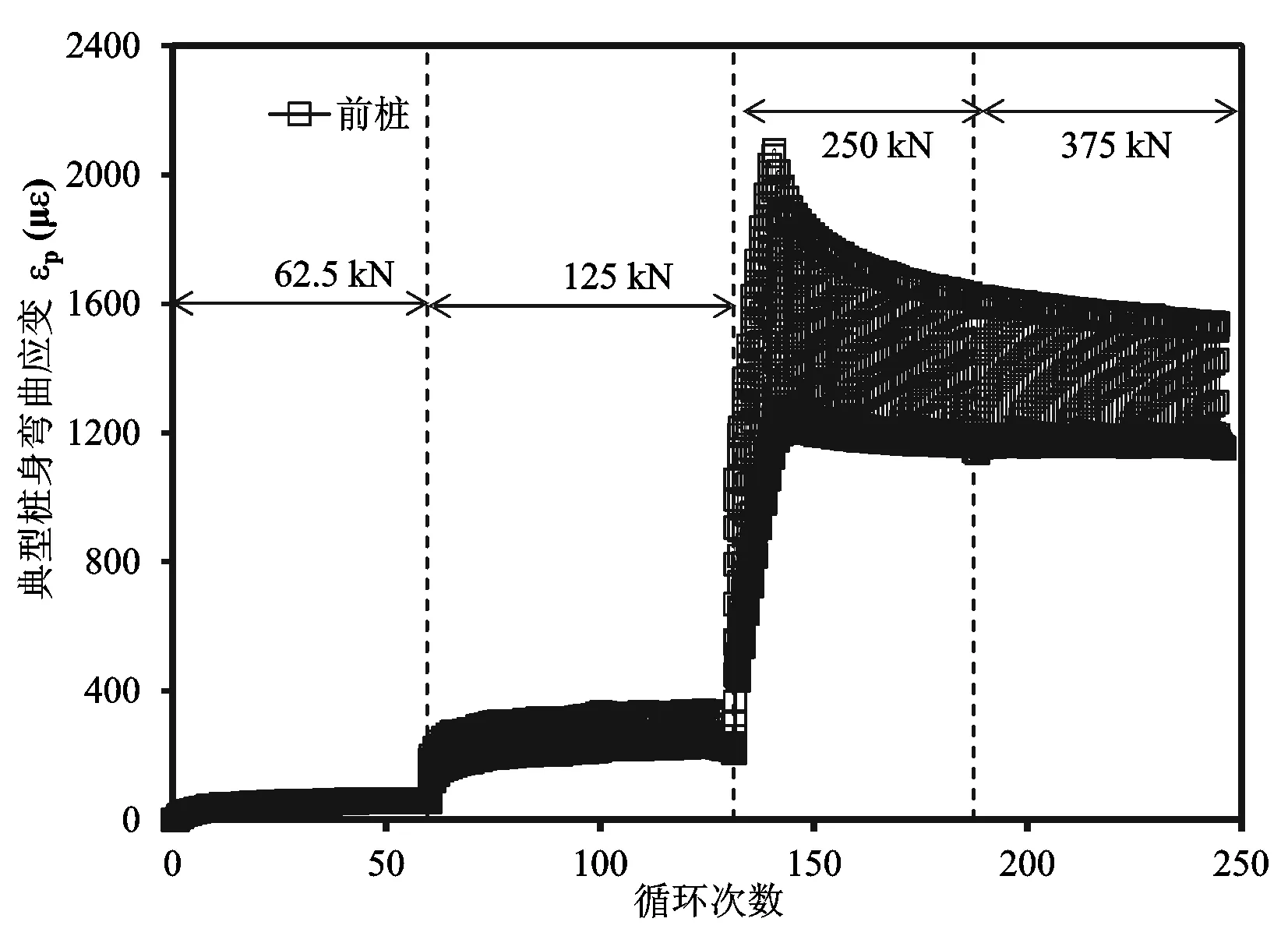
图9 循环加载卸载条件下桩基弯曲应变值变化曲线Fig.9 Typical bending strain induced in the existing pile due to cyclic loading and unloading

图9为典型的循环加载—卸载作用导致的桩基弯曲变形。与单桩情况类似，随着循环加载—卸载，桩基发生弯曲变形。当桩基受到加载作用时，桩的弯曲变形增大；当卸载作用时，桩基的弯曲变形减小。但是值得注意的是，当荷载完全卸载后，桩基的弯曲变形量并未减少到0。即在加载—卸载循环过程中，桩基产生了残余的弯曲变形。这是由于循环荷载引起了桩周土产生了不可恢复的塑形变形。

对于桩基的残余弯曲应变来说，其随着水平循环荷载增大而增大，减小而减小。然而，在水平循环荷载达到250 kN之前，桩基的最大弯曲应变随循环加载次数而增加。当水平荷载大于250 kN时，桩的最大弯曲应变反而随着加载次数的增加而降低。当水平循环荷载从62.5 kN增加到250 kN，桩的最大弯曲应变从65με变化到2 050 με，最终降低为1 530 με。当水平循环荷载从62.5 kN增加到375 kN，桩的最大残余弯曲应变从50 με增加到1 150 με。

3.4 循环荷载与桩基弯曲变形之间的关系

图10-a显示了桩基最大弯曲应变值和循环荷载值之间的变化关系。由于受到桩帽和周围土体的约束作用，桩基的弯曲应变最大值发生在地表以下。对于前排桩(靠近荷载施加装置的桩)来说，当受到的水平循环荷载值为62.5 kN、125 kN、250 kN和375 kN时，桩基的弯曲应变值分别为211με、607με、2 186με和1 956με。后排桩(远离荷载施加装置的桩)的最大弯曲应变值分别为200με、533με、1 400με和609 με。从试验结果对比来看，当施加的水平循环荷载值较大时，后排桩的最大弯曲变形值远小于前排桩。对于本次试验中群桩的布置方式来说，水平循环荷载引起的前排桩弯曲应变值是后排桩弯曲应变值的3.2倍左右。

图10-b为桩基最大残余弯曲应变值和受到的循环荷载值之间的变化关系。当循环荷载值减小到0时，桩基内的弯曲应变值为残余弯曲应变。与最大弯曲应变值一样，前排桩的残余弯曲应变值远大于后排桩的残余弯曲应变值。本次试验中，前排桩的最大残余弯曲应变值是后排桩弯曲应变值的3.1倍。为了减少水平循环荷载如波浪荷载对桩基的影响，工程中应对前排桩进行加固，比如采用更大直径的桩。试验结果同样表明桩基的残余弯曲应变值远小于最大弯曲应变值，前排桩最大残余弯曲应变值同最大弯曲应变值的比率在0.28～0.59之间，而后排桩的这个参数范围在0.23～0.82之间。

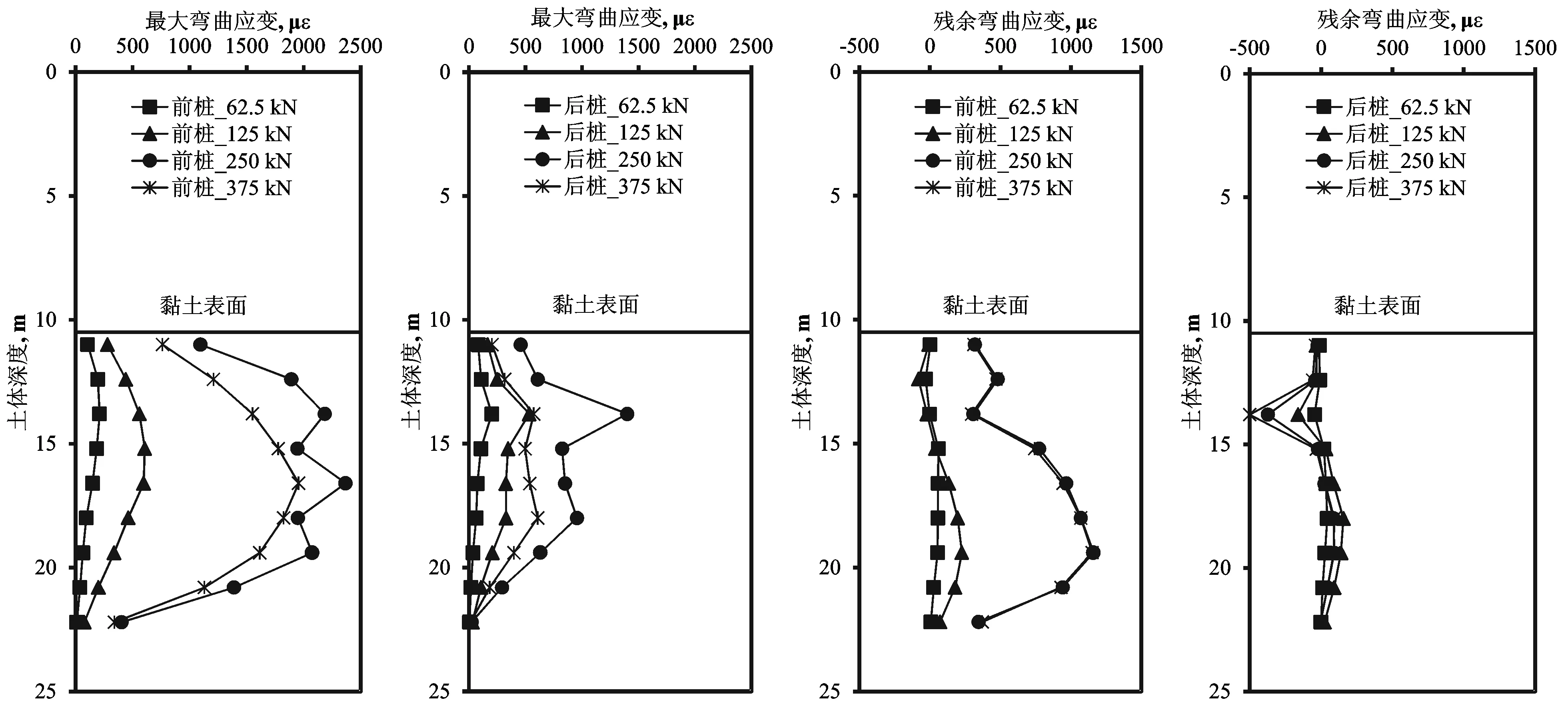
10-a 最大弯曲应变 10-b 残余弯曲应变图10 循环荷载与引起的桩基弯曲变形之间的关系曲线Fig.10 Relationship between bending strain induced in the existing pile and applied cyclic load

4 结论

本文重点介绍水平循环荷载作用下群桩的离心模型试验。基于离心试验结果，可得出以下结论：

(1)当施加水平荷载值逐渐增大时，桩基向前发生位移；当荷载逐渐减小时，桩基向后发生位移。然后，在每个加载—卸载循环后，桩基无法恢复位移到初始位置，表明循环加载—卸载作用使得桩基产生了残余位移。主要原因是循环加载—卸载导致桩周土发生强度弱化。

(2)在每个加载卸载循环过程中，随着施加荷载值的增大，引起桩基的最大位移和残余位移同时增加。当施加的最大荷载从62.5 kN增大到375 kN时，引起群桩桩顶的最大水平位移从26.0 mm增大到1 134 mm，残余水平位移从7.6 mm增大到952 mm。群桩桩顶的残余水平位移与最大水平位移的比值介于0.3～0.84。

(3)每次加卸荷循环后，桩体内均产生残余弯曲应变。在水平循环荷载作用下，群桩的前排桩产生的弯曲应变值是后排桩的3.2倍。因此实际工程中，应加强前排桩的抗弯性能。对于前排和后排桩来说，桩基残余弯曲应变值同最大弯曲应变值的比率在0.23～0.82之间。

(4)相同荷载作用下(即群桩模型中每根单桩所分担的水平荷载与单桩模型中单桩水平荷载相同)，群桩整体最大位移、残余位移小于单桩，群桩桩基残余位移值同最大位移值比值大于单桩。这表明，群桩整体较大刚度限制桩体位移，同时也减弱桩体相互作用。

参考文献：

[1] 张卫，孙百顺.港口水工建筑技术国家工程实验室资金申请报告[R]. 天津：交通运输部天津水运工程科学研究院，2012.

[2] 陈仁朋，顾明，孔令刚，等. 水平循环荷载下高桩基础受力性状模型试验研究[J]. 岩土工程学报，2012, 34(11)：1 990-1 996.

CHEN R P, GU M, KONG L G, et al. Large-scale model tests on high-rise platform pile groups under cyclic lateral loads[J]. Chinese Journal of Geotechnical Engineering , 2012, 34(11)：1 990-1 996.

[3] 包承纲, 饶锡保. 土工离心模型的试验原理[J]. 长江科学院院报, 1998, 15 (2)：2-7.

BAO C G, RAO X B. Principle of the Geotechnical Centrifuge Model Test [J]. Journal of Yangtze River Scientific Research Institute, 1998, 15 (2):2-7.

[4] Lei G, Shi J. Physical meanings of kinematics in centrifuge modeling technique [J]. Rock and Soil Mechanics，2003, 24(2): 188-193.

[5] Brandenberg S J, Boulanger R W, Kutter B L， et al. Static Pushover Analyses of Pile Groups in Liquefied and Laterally Spreading Ground in Centrifuge Tests [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133 (9): 1 055-1 066.

[6] Zhang L M, Kong L G. Centrifuge Modeling of Torsionally Loaded Pile Groups [J]. Journal of Geogechnical and Geoenvironmental Engineering, 2007, 133 (11): 1 374-1 384.

[7] 王军，蔡袁强，徐长节，等. 循环荷载作用下饱和软粘土应变软化模型研究[J]. 岩石力学与工程学报，2007,26(8):1 713-1 719.

WANG J, CAI Y Q,XU C J, et al. Study on strain softening model of saturated soft clay under cyclic loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2007,26(8):1 713-1 719.