多尺度格网的耕地信息无损提取与表达<br/>——以山西省芮城县为例

多尺度格网的耕地信息无损提取与表达
——以山西省芮城县为例

2018-05-10王鹏毕如田徐振高阳

生态环境学报 2018年4期

王鹏，毕如田，徐振，高阳

山西农业大学资源环境学院，山西太谷 030801

资源环境信息通过格网化方法可表达其空间分布与分异规律，可匹配、融合多源数据，实现资源环境数据空间模型的构建和表达（王卷乐等，2015）。格网化方法已在土地利用（Koga et al.，2016）、城市管理（李德仁等，2007）、地理国情监测（李德仁等，2014；王妍程等，2016）、林业（吴东亮等，2007）和生态环境管理（左伟等，2003）等领域得到广泛应用。尺度是生态学研究的基本概念之一，也被广泛应用于地理学研究中（岳文泽等，2005；刘学军等，2007；王晓明等，2005）。在地理学中，尺度指地理范围、详细程度及时间频率（张迁迁等，2015）。多尺度格网是指用不同尺度格网将指定范围划分成不同大小层次的网格，实现对全区域的无缝覆盖，每个层次的网格，在范围上具有上下层涵盖关系（李德仁等，2005）。由于气候、地貌、土壤、土地利用等不同类型的资源环境信息在不同空间尺度上存在着多尺度效应（张迁迁等，2015；毕如田等，2012；高艳等，2010），传统的格网化方法会导致属性信息的缺失（白燕等，2010）。Galton（2003）系统地研究了在矢量数据格网化过程中空间属性随尺度变化的敏感程度，某些属性的丢失，实质上是一种面积误差。连世忠等（2017）提出了一种顾及空间自相关的地理国情信息统计格网尺度选择方法。因此探索不同尺度下空间信息的无损提取和表达对于准确掌握资源环境信息具有重要作用。

耕地资源是资源环境最重要的组成部分之一，耕地信息的无损提取和格网化表达对耕地资源管理具有重要意义。对耕地的格网化表达研究发现，传统的格网化方法多以面积占优法（Rule of Max Area，RMA）为基础，重点研究格网尺度对格网化表达精度的关系，但一定程度上忽略了RMA方法对于格网化表达精度的影响。采用RMA格网化方法的精确性依赖于最佳格网尺度的选择，格网尺度大于或小于最佳格网尺度时，耕地会呈现扩张或压缩的趋势，无法准确表达耕地的数量和质量信息；也无法表达格网单元覆盖范围内耕地面积小于设定阈值的耕地面积及其分布情况。对于耕地资源单要素而言，使用RMA方法格网化近似于二值化处理，其结果只能反映某格网单元内是否为耕地，不能表达耕地资源空间分布的渐变规律。鉴于此，在耕地单要素属性信息无损格网化提取的基础上，提出了以格网中耕地面积占格网面积的比值即格网耕地纯度指数来表达耕地多尺度空间分布的方法，实现了自底向上的多尺度属性信息快速提取，可根据不同需求从底层数据中提取生成多尺度的耕地格网数据，为耕地资源的精细化管理提供支持。

1 研究方法

1.1 格网划分方法

地理格网的划分依据主要有两种：经纬度坐标格网和高斯-克吕格投影直角坐标格网，其中，前者受纬度影响较大，低纬度和高纬度地区的格网面积和形状有明显的差异。后者在同一投影下，所有格网的形状和大小都相同，利于耕地格网化表达过程中面积的计算（陈彦清等，2014）。由于在耕地格网化表达和数据提取时，要求面积不变或在允许误差范围以内，因此本研究选用高斯-克吕格投影直角坐标格网进行分析。

1.2 耕地信息无损格网化表达方法

1.2.1 基础格网尺度的选择

在典型地貌土地利用现状矢量数据栅格化尺度效应的研究中，通过RMA法对该土地利用数据进行不同尺度的栅格化处理，分析得出：当格网单元的大小为30 m×30 m时，在不同典型地貌中耕地面积误差百分比均小于1%（王健欣，2013），可满足精度的需求。借鉴全球等经纬度四叉树剖分体系（Geographic Subdividing grid with One dimension coding on 2n-Tree，GeoSOT）中格网尺度的设置方法，该方法采用2n为各级格网尺度，在向下剖分时可避免小数带来的计算困难，以实现精确四叉剖分。因此本研究选择最接近30 m的25m作为基础格网尺度，既能满足格网化表达过程中的精度要求，又能为以后更高精度要求小尺度格网划分提供向下连续剖分的数据基础。

1.2.2 矢量数据预处理

对矢量数据进行属性值规范化处理，参照GB/T21010—2007《土地利用现状分类》，将土地利用类型分为：耕地、园地、林地、草地、城镇村及工矿用地、交通运输用地、水域及水利设施用地、其他土地。耕地的土壤类型根据《中国土壤分类与代码》（GB/T17296—2009）将土类、亚类、土属、土种进行规范化命名。耕地土壤养分属性值规范化采用均值替换法（Mean Imputation）处理异常值和空值。

1.2.3 创建基础格网

本研究在ArcEngine二次开发平台支持下，基于高斯-克吕格投影平面直角坐标系统，以研究区行政界线外包矩形范围创建大小为512 m×512 m的格网。采用四叉剖分方法将该格网向下剖分至 32 m×32 m的基础格网，生成512 m×512 m、256 m×256 m、128 m×128 m、64 m×64 m、32 m×32 m的多尺度格网数据集，在创建格网的同时创建唯一标识码，用于属性提取运算。

1.2.4 耕地单要素属性信息无损格网化表达及格网耕地纯度计算

经数据预处理后提取出矢量耕地数据，将其与创建的32 m基础格网进行叠加分析，计算每个格网单元中的耕地面积。保留格网单元的耕地面积属性值，保证格网数据中耕地面积与矢量耕地数据的面积完全相同，实现耕地单要素面积属性的无损格网化表达。根据格网大小和格网中耕地的面积计算格网耕地纯度指数I，具体计算公式为：

式中，Ac为格网中耕地的面积；Ag为该格网的面积。通过耕地纯度指数定量化表达格网覆盖范围中耕地的面积和空间分布。为了形成全区域连续无缝的格网并方便后续提取运算，对与耕地图斑没有相交关系的格网采取不删除的方式，通过RMA方法为格网赋属性值，为表达耕地空间分布提供参照。具体方法是：在保留耕地面积属性字段的情况下，新增加 1个地类面积属性，将该格网与土地利用现状数据进行再次叠加，通过RMA方法确定格网的地类类型、土壤类型、土壤养分等属性信息。

1.3 多尺度格网属性信息提取方法

多尺度格网数据在空间范围上主要表现为两种形式：（1）不同尺度格网的尺度缩放因子成整数倍数关系，大尺度格网完整包含小尺度格网，不同层的数据完整覆盖，不交叉；（2）不同尺度格网的尺度缩放因子不成整数倍数关系，大尺度的格网不能完整包含小尺度格网，不同层的数据存在交叉（张小虎等，2014）。

本研究中多尺度格网数据由顶层格网四叉剖分得到，大尺度的格网完全包含小尺度格网，格网大小成倍数关系，属于第1种形式。因此在基于基础格网数据进行属性提取时，首先确定尺度缩放因子 n（n=2，4，····），n 目标格网的大小为 n×n 个基础格网。如n=2时，目标格网属性值由4个基础格网提取得到，如图1所示。

图1 格网信息提取示意图Fig.1 Sketch map of grid information extraction

相同空间位置上目标格网耕地面积等于 n×n个基础格网的耕地面积之和，以保证耕地面积属性的无损提取；目标格网的耕地土壤养分属性采用地类面积加权平均的方法确定，目标格网的其余各属性值通过面积占优法提取。面积加权平均计算公式为：

式中，n为尺度缩放因子；Ai为第 i个基础格网的地类面积；Ni为第i个基础格网的土壤养分值；N为目标格网的土壤养分属性值。

根据基础格网数据的顺序编码和行列数自左下向右上依次进行迭代运算，实现整个研究区数据提取。通过改变尺度缩放因子实现多尺度耕地格网数据提取。多尺度格网生成、多尺度耕地属性信息提取和耕地纯度指数计算均在ArcEngine二次开发平台下运用C#语言编程实现。

1.4 分析方法

1.4.1 多尺度耕地格网面积误差分析

分别对多尺度耕地格网数据和县域矢量耕地数据的耕地面积进行汇总，并计算耕地面积误差。具体计算公式为：

式中，Ag表示耕地格网化后得出的面积；Av表示耕地矢量数据的面积；E表示耕地面积误差，正值表示耕地面积比实际大，负值表示耕地面积比实际小。

耕地面积误差百分比的计算公式为：

式中，Y表示耕地面积误差百分比，当Y＜0时，表示格网化表达后耕地面积收缩；Y＞0时，表示格网化表达后耕地面积扩张。

本研究通过对使用无损格网化法和使用面积占优法得到的耕地面积与研究区矢量数据的耕地面积进行面积误差分析。

1.4.2 多尺度耕地格网数据空间分布的一致性检验

本研究采用标准差椭圆模型检验多尺度耕地格网数据与原始耕地图斑空间分布情况。标准差椭圆方法（Standard Deviational Ellipse，SDE），是用于精确揭示地理要素的空间分布特征的方法（Warntz et al.，1960）。SDE中的平均中心（Mean Center）是以要素的某一属性为权重对所有要素的x，y值进行加权平均。SDE的方位角反映分布的主趋势方向，SDE的长轴与短轴长度为标准距离，分别表示要素在主趋势和次要方向上的离散程度。首先计算平均中心：

式中，Wi为要素权重；xi，yi为要素的质心坐标；n为要素个数；为要素平均加权中心。其次，计算SDE，公式为：

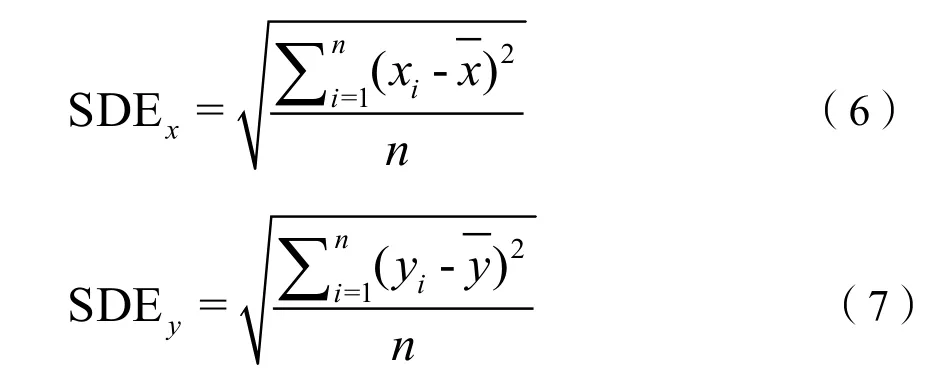
式中，SDEx为标准差椭圆短半轴长度；SDEy为长半轴长度；n为要素个数。最后计算旋转角θ，公式为：

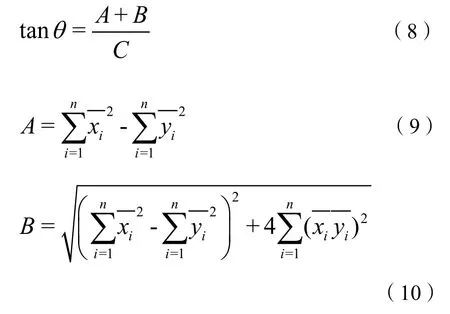
本文以格网耕地纯度指数和耕地图斑的面积作为权重，分别计算多尺度耕地格网数据和矢量耕地数据的平均中心和空间分布方向角，比较二者的平均中心和空间分布方向角的差异，差异越小，说明该多尺度格网数据越能正确反映耕地空间分布。

1.4.3 基于耕地纯度指数的耕地空间分布尺度特征分析

对各尺度耕地格网数据的耕地纯度指数进行分级，统计各级纯度指数范围的格网数及其占整个耕地格网的比重，分析研究区耕地资源在不同尺度下的空间分布特征。对比分析RMA格网化方法与格网耕地纯度指数在不同尺度下表达耕地资源空间分布的差异。

2 研究区与数据处理

2.1 研究区及数据来源

本研究以山西省芮城县为例进行耕地信息无损提取与表达研究。芮城县位于山西省南端，地处中条山南部，黄河北面，东西长，南北窄，北高南低，为典型黄土丘陵及阶地台塬区，地理坐标为110°16′～110°58′E，34°35′～34°51′N。基础数据为山西省芮城县1∶1万土地利用现状数据库。耕地矢量数据从该县1∶1万土地利用现状成果数据中提取得到。数据坐标系为西安80坐标系，高斯-克吕格3度分带。

2.2 数据处理

（1）对土地利用现状矢量数据进行属性值规范处理，以该县行政区界线的外包矩形为范围生成512 m×512 m的省级格网，通过四叉剖分方法将该格网向下逐级剖分至32 m×32 m的基础格网，生成多尺度格网数据集，其规模为 912×2096的共1911552个的格网单元。

（2）将32 m基础格网与县域耕地数据进行叠加分析，计算各格网单元中的耕地面积，其中与县域耕地数据有相交关系的格网有476851个。计算该格网中各格网单元的耕地纯度指数，完成耕地单要素无损格网化表达。为实现基于基础格网的统一的属性提取运算，保留与县域土地利用现状数据没有相交关系的格网。

（3）将带有耕地面积属性的基础格网和土地利用现状数据进行再次叠加，得到与县域土地利用现状数据有相交关系的格网有1152074个。根据上文研究步骤进行基础格网属性赋值。为实现基于基础格网的统一的属性提取运算，保留与县域土地利用现状数据没有相交关系的格网。

（4）在ArcEngine二次开发平台支持下，基于32 m耕地格网数据，运用C#语言依次以缩放因子n=2，4，8，16逐级进行属性信息提取和耕地纯度指数计算，生成64、128、256、512 m多尺度耕地格网数据集。

3 结果与分析

3.1 多尺度耕地格网面积误差分析

采用上述误差分析方法进行尺度耕地格网面积误差分析，结果如表1和图2所示。通过无损格网化方法得到的多尺度耕地面积误差均为0.1 m2，而使用RMA方法得到的不同尺度的耕地面积误差随格网尺度的变化而变化，格网尺度为32 m和64 m时耕地面积误差百分比小于1%，格网尺度为128、256和512 m时耕地面积误差百分比不断增大，其中格网尺度为 512 m时面积误差百分比达到了11.65%。

表1 耕地面积误差统计表Table1 The statistical table of cultivated land area error

图2 耕地面积误差百分比Fig.2 The percent of cultivated land area error

3.2 多尺度耕地格网数据空间分布的一致性检验

根据式（5）～（11）计算该县矢量耕地数据和各尺度耕地格网信息数据的平均中心坐标和标准差椭圆旋转角度，得到该县矢量耕地分布的平均中心坐标为（37464030.3，3839694.2），耕地空间分布标准差椭圆的旋转角为80.30°，如图3所示。多尺度耕地格网数据的平均中心和空间分布标准差椭圆的旋转角如表2所示，与原矢量耕地数据的平均中心相差 0.1～0.8 m，旋转角相差 0.01°～0.05°。

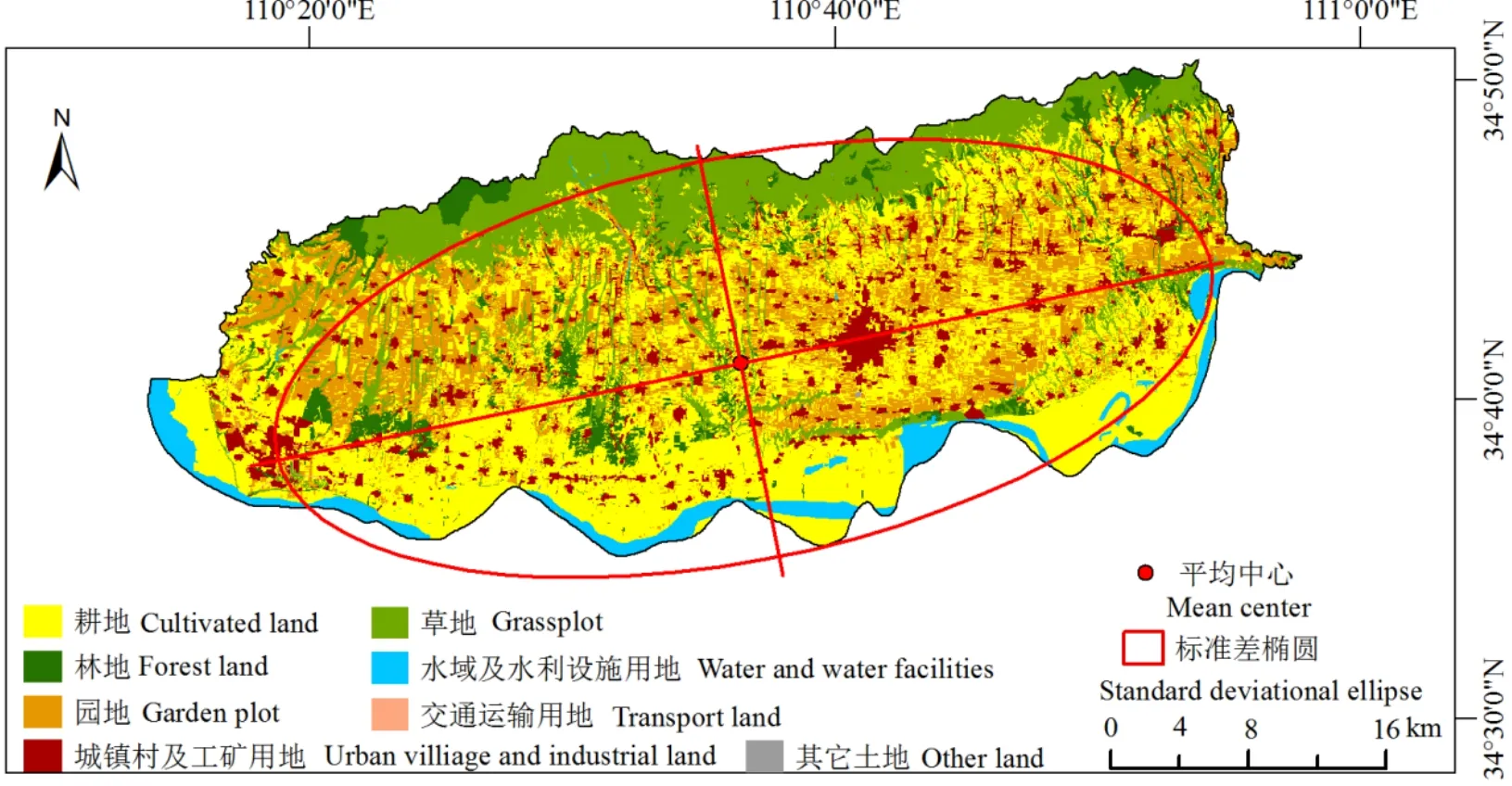
图3 耕地空间分布图Fig.3 The map about spatial distribution of cultivated land

表2 不同尺度耕地格网标准差椭圆模型计算结果Table2 The calculation results of SDE for cultivated land on different scales

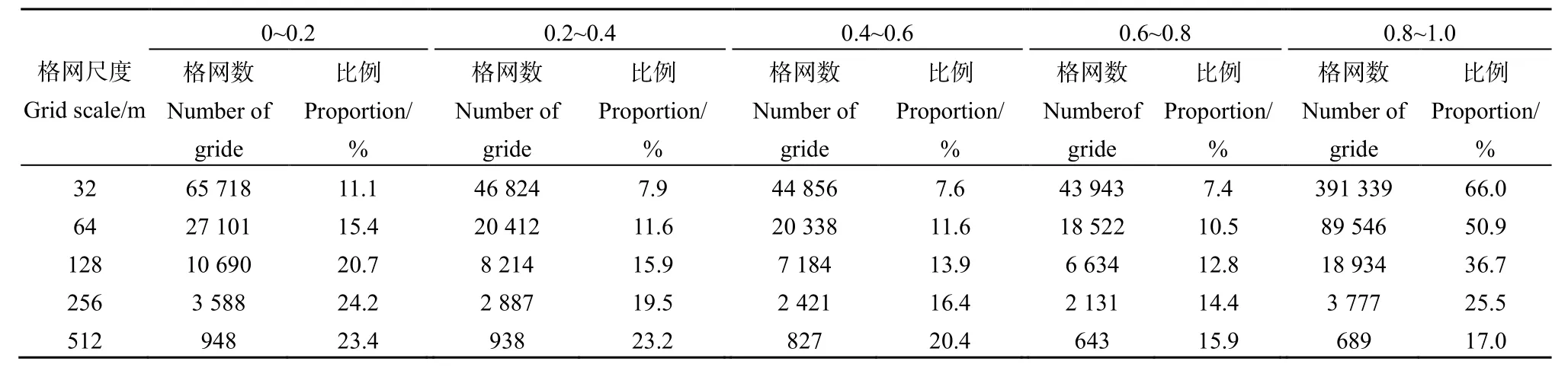
表3 不同尺度格网单元耕地纯度分布表Tale 3 The purity distribution of different scale grid cell

3.3 基于格网耕地纯度指数的耕地空间分布尺度特征分析

对多尺度耕地格网数据集的格网耕地纯度进行分级（0～0.2，0.2～0.4，0.4～0.6，0.6～0.8，0.8～1.0），统计各级格网耕地纯度的分布情况，结果如表 3所示。随着格网尺度从32～512 m逐级增大，纯度指数在0.8～1.0的格网数量比重迅速减少，其他纯度指数的格网数量比重呈增长趋势。以研究区内耕地破碎与集中连片交接区域为例，分别制作基于面积占优方法的多尺度耕地空间分布专题图（图4）和基于耕地纯度指数的多尺度耕地空间分布图专题图（图5）。如图4所示，在耕地破碎地区耕地的格网随尺度逐级增大可能会被判定为非耕地，耕地集中连片区域周边的非耕地格网随尺度逐级增大可能被判定为耕地，从而导致误差逐渐变大。如图 5所示，随格网尺度逐级增大，耕地纯度指数呈现出一定的变化规律：在耕地集中连片区，格网耕地纯度指数在原值上下小范围浮动；在耕地破碎地区，格网耕地纯度指数急剧下降，正向值趋于0，表示该区域有耕地分布但面积较小。

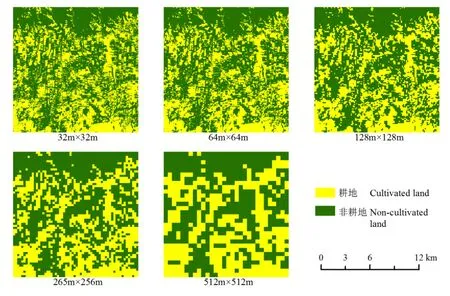
图4 基于面积占优法的耕地空间分布示意图Fig.4 Thesketch map of spatial distribution of cultivated land based on the Rule of Max Area

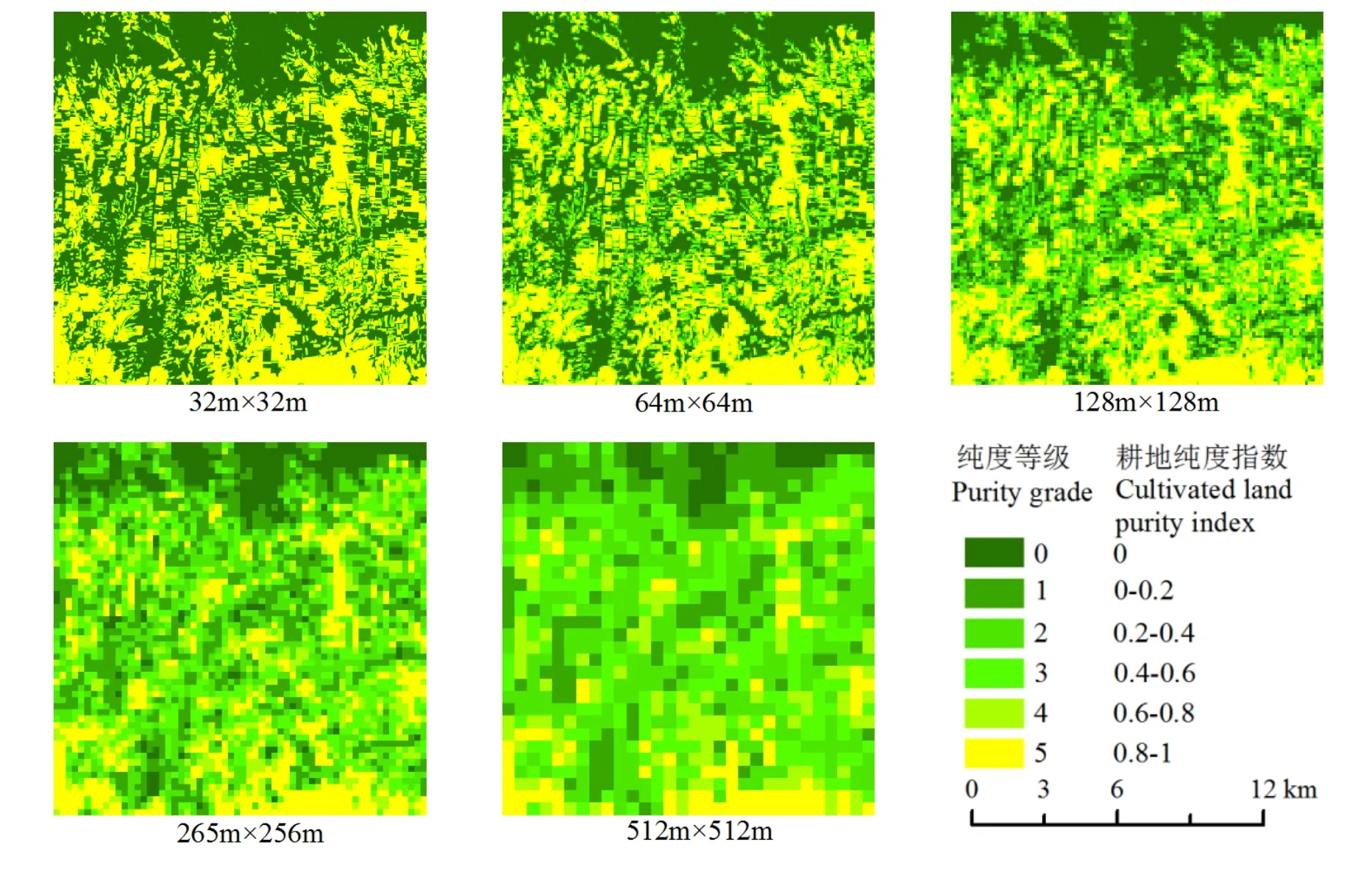
图5 基于格网纯度指数的耕地空间分布示意图Fig.5 The sketch map of spatial distribution of cultivated land based on grid purity index

4 讨论

格网化的误差与格网单元大小、多边形的结构和算法有很大关系（Shortridge，2004），矢量数据多尺度格网化过程存在精度失损问题（杨存建等，2001）。本研究由耕地面积无损提取方法得到的不同尺度的耕地面积误差均为0.1 m2，该误差来源于计算过程中的舍入误差，相对于全县488111225.1 m2耕地，可忽略不计。在格网尺度较小时，采用无损格网化方法和RMA方法处理的面积误差相差不大，随着格网尺度逐级增大，RMA方法会呈现误差逐级增大的分布特征（刘明亮等，2001），说明RMA格网化方法的准确性依赖于格网尺度的大小。因此，基于多尺度耕地信息无损提取方法，可以在任何尺度下准确表达耕地的面积信息。

对该多尺度格网数据耕地面积进行提取汇总，能满足统计上的一致性，在空间分布一致性检验中，陈彦清等（2014）通过标准差椭圆模型对不同尺度耕地资源空间分布相似性进行了验证。标准差椭圆模型可以查看要素分布是否被拉伸，并以中心、长轴、短轴、方位角为标准差椭圆的基本参数（Zhao et al.，2012）。本研究中该县域面积为1178.8 km2，从表 2可以看出，各尺度耕地格网数据与原矢量耕地分布的平均中心相差均小于1 m，偏差很小；各尺度耕地格网数据与原矢量耕地空间分布标准差椭圆的旋转角相差均小于0.1°，在0°～180°范围之间，偏差可忽略不计。因此，该多尺度格网数据的耕地空间分布与原矢量耕地数据保持高度一致。

在耕地资源空间分布地图表达过程中，传统的面积占优法只能将耕地面积占优的格网表示为耕地，无法表达耕地面积不占优的格网中的耕地分布。耕地纯度指数法可将耕地面积不占优的格网中的耕地（如图5中耕地纯度指数在0～0.4范围内的格网）通过色调进行空间表达，形成了一个连续渐变的耕地纯度指数面（图5），不仅能通过不同色调和尺度特征反映该区域耕地空间分布渐变特征和集中连片情况，而且能通过耕地纯度指数和格网大小准确计算格网中的耕地面积。

5 结论

本文以位于黄土丘陵区的山西省芮城县为实例，对基于多尺度格网的耕地信息无损提取与表达方法进行了验证，得出如下结论：

（1）通过耕地面积无损提取方法得到的不同尺度的耕地面积误差均为0.1 m2（可忽略不计）。实现了多尺度格网的耕地面积无损提取，表明无损格网化方法能精确地提取耕地数量信息。

（2）经标准差椭圆模型（SDE）验证，该多尺度耕地格网数据与原矢量耕地的平均中心相差小于1 m，标准椭圆角旋转度相差小于0.1°，表明该多尺度耕地格网数据可以准确反映耕地资源的分布情况。

（3）通过基于格网耕地纯度指数的耕地空间分布尺度特征分析，得出基于耕地纯度指数的方法能够实现不同尺度下耕地空间分布的定量化表达。对比RMA格网化方法处理结果，基于格网耕地纯度指数的多尺度表达方法更能准确表达和展示耕地资源专题信息。

参考文献：

GALTON A. 2003. Granularity-sensitive spatial attributes [J]. Spatial Cognition and Computation, 3(2-3): 97-118.

KOGA T, KAWAMURA A. 2016. Assessing impervious area ratios of grid-based land use classifications on the example of an urban watershed [J]. Procedia Engineering, 154(9): 609-616.

SHORTRIDGE A M. 2004. Geometricvariability of raster cell class assignment [J]. International Journal of Geographical Information Science, 18(6): 539-558.

WARNTZ W, NEFT D. 1960. Contributions to a statistical methodology for areal distributions [J]. Journal of Regional Science, 2(1): 47-66.

ZHAO Y, YANG Z Y, HAO L S, et al. 2012. The evolution of spatial displacement pattern of China's crude oil flow source-sink system [J].Acta Geographica Sinica, 67(4): 455-466.

白燕, 廖顺宝. 2010. 矢量数据属性信息无损栅格化的实现方法——以全国 1∶25万土地覆被数据为例[J]. 地球信息科学学报, 12(3):385-391.

毕如田, 高艳. 2012. 典型地貌景观指数的多尺度效应分析——以山西省运城市为例[J]. 地球信息科学, 14(3): 338-343.

陈彦清, 杨建宇, 张超. 2014. 基于网格的耕地质量分等成果省级汇总方法[J]. 农业工程报, 30(24): 280-285.

高艳, 毕如田, 曹毅. 2010. 空间粒度变化及土地利用分类对景观指数的影响——以山西省闻喜县为例[J]. 中国生态农业学报, 18(5):1076-1080.

李德仁, 李宗华, 彭明军, 等. 2007. 武汉市城市网格化管理与服务系统建设与应用[J]. 测绘通报, (8): 1-5.

李德仁, 邵振峰, 丁霖. 2014. 地理国情信息的多级网格化表达[J]. 地理空间信息, 12(1): 1-9.

李德仁, 邵振峰. 2005. 空间信息多级网格及其功能[J]. 地理空间信息,3(4): 1-3.

连世忠, 丁霖, 陈江平. 2017. 顾及空间自相关的地理国情信息统计格网尺度选择——以植被覆盖信息为例[J]. 测绘通报, (3): 46-51.

刘明亮, 唐先明, 刘纪远, 等. 2001. 基于1 km格网的空间数据尺度效应研究[J]. 遥感学报, 5(3): 183-190.

刘学军, 卢华兴, 仁政, 等. 2007. 论 DEM 地形分析中的尺度问题[J].地理研究, 26(3): 433-442.

王健欣. 2013. 典型地貌土地利用现状矢量数据栅格化的尺度效应及误差分析[D]. 山西: 山西农业大学: 58.

王卷乐, 孙九林. 2015. 格网化资源环境综合科学调查的若干问题思考[J]. 地球信息科学学报,17(7): 758-764.