数字峰值测量的新方法——双频峰值检波法

王丹琦，阿地力·依米提，张 莉

（1.新疆师范大学 物理与电子工程学院，新疆 乌鲁木齐 830054；2.新疆农业大学 科学技术学院，新疆 乌鲁木齐 830052）

文章所介绍的一种数字峰值测量的新方法，是依据等效采样的原理，利用较低采样率的A/D采样那些频率甚至比A/D采样率高很多的信号的峰值。本峰值检波电路基于信号频域频谱搬移理论，采用两个特殊频率（双频）对信号先后完成采样，互补采样中的“盲区”，通过采样的最大值提取得到周期信号的峰值。这种方法可以兼顾高低频，全幅度段达到良好的线性。可以做到0.1Hz-100MHz频率段，同时，此检峰原理很有研究价值，变换灵活，在具体设计电路时考虑实际频率段的需求来做设计，可以将此电路的性能应用的灵活自如。

以FPGA［1］实现峰值测量精度高，实现较为容易。在FPGA内部设置两个寄存器，分别存储目前为止测量到的最大值（REGM）和最小值（REGL）。下一个信号被采集进来以后，分别与这两个寄存器的数据比较，若大于原来的最大值，就用这个值替代REGM中的数据；如果小于最小值，就用这个值代替REGL中的数据；否则，等待下一采样值的来临。每个信号周期结束以后，REGM和REGL的差值就是峰值。

数字测量的精度和采样的A/D有很大的关系，随着A/D的选用不同，精度可以做的很高。另外稳定性也要比模拟峰值检波高，避免了模拟期间不稳定或者漂移等因素的影响，减小了峰值检测的误差。采用A/D采样［2］的方法采集峰值，对于采样点数的要求也比较高。通常情况下，保持波形失真度小，要求波形至少由64个点组成（当然这个也要根据实际需要，若不需要精度很高可以适当减少点数）。

1 频谱搬移理论分析

Fs为信号抽样频率，Fx为被抽样信号的频率，N为采样点数。对于任意周期信号要采完一个周期才能确定其峰值［3］。分析当Fs=10KHz时，对于1Hz的任意周期信号要采完一个周期才能确定其峰值，那就是要采样10000个点，即N=10000。对全频带内信号分析：进采样以后的信号频谱也是成周期性的，即以Fs频谱搬移。对于［0，Fs］内的频谱就可以包含信号的全部信息，即对于［0，Fs］区间来说有且仅有一根信号有效频率成分对应的谱。所以，当可以采样［0，Fs］信号的全部峰值时，就可以断定全频带的信号都可以采到峰值。

很明显，Fs为10KHz时，0～1Hz的信号是没有采全一个周期的，就没法判断任意周期信号的峰值了，将这段区间定义为盲区。

所以，搬移到整个频域，每个频段内都存在一部分信号采样的盲区，在盲区里，系统无法判断是否采到了信号的最大值。

1.1 （0～Fs）频谱盲区分析

Fs=10KHz进行信号抽样时，频谱上信号的盲点在-1Hz～+1Hz，同样，搬移后，盲点也会搬移。根据采样定理分析，信号频谱关于nFs对称（n=…-3，-2，-1，0，1，2，3…），基于这个对称关系得知，信号频谱在nFs左右的（-1Hz～+1Hz）都是采样信号盲区。同时，根据信号频谱分布理论，信号也关于Fs/2对称，所以可以得出，信号频谱关于nFs/2的整数对称。

1.2 （0～Fs/2）频谱盲区分析

基于信号关于nFs/2也对称，分析信号频谱在（0～Fs/2）内的盲点。明显可以判读当Fs=10KHz，Fx=5 KHz时候是采不到信号幅值的。因为信号在5KHz左右也有盲区。与采样Fx=10KHz的信号不一样，它的盲区在5KHz旁边的（-0.5Hz～+0.5Hz）。比较两种采样，如果用等效采样看待这个问题是很好理解的。如图1所示：第一个波形就是实时采样采信号的示意图，第二个图是等效采样的示意图，通过步进t的采样重组波形。

Fx=10KHz时，采样盲点为（-1Hz～+1Hz），将其重组波形，等效于采（-1Hz～+1Hz）的周期信号，所以采不到信号的一个周期值，及盲区为（-1Hz～+1Hz）。而对于Fx=5KHz的信号同样用10KHz的抽样率采值，在波形重组时可以看出在5KHz左右的（-0.5Hz～+0.5Hz）是盲区。如Fx=5.005KHz的信号经Fs=10KHz采样时，采点N=10000时正好可以重组出一个周期波形来。可以得出结论，Fs=10KHz时，在Fs/2的旁边存在盲区，且只有（-0.5Hz～+0.5Hz）。这与Fs旁边的盲区相比，宽带缩短一半。

图1 实时采样和等效采样图

1.3 （0～Fs/n）频谱盲点分析

同上面的推导类似，很容易想到信号在Fs/3，Fs/4的时候同样存在盲区，在信号频率为Fs/4时，盲区在Fs/4的两边（-0.25Hz～+0.25Hz）的范围内。在Matlab里仿真，如Fs=10K，Fx=2500.25Hz，N=10000时刚好可以得到信号的一个周期波形。如图2所示，为了直观的看到信号是10000个点一个周期，用Matlab仿真的时候取了N=20000个点，可以看出是两个整的周期。但也可以看出信号已经不再是正弦波形，其点是杂乱的按一定抽样顺序排列的，这就是在信号抽样的过程中发生相位翻转造成的，如果要按某些特殊规律排序就可以完整的得到一个频率为2500.25Hz正弦波。

同样，推到更广的范围去谈这个问题，频谱在Fs/n的左右都会存在盲区，且盲区范围为（-1/nHz，+1/nHz），只有在盲区内，此数值采样才采不到信号的一个整周期，系统无法确定周期信号的峰值。

图2 N=20000个点的边界采值波形

1.4 选取双频补回盲区

从上面推导的结论可以知道，在用一个采样率如Fs=10KHz抽样信号，都会存在盲区。

普遍的来讲，抽样率为Fs，如果对最低频极限情况F1采样，采一个周期需要采的点数N=Fs/F1，第一个盲区就出现在Fs的左右［-F1～+F1］，第二个盲区在Fs/2的左右［-F1/2，+F1/2］，第n个盲区出现在Fs/n的左右［-F1/n，+F1/n］。

那怎么补回这些盲区？双频的作用也就是在这里。如果Fs=10KHz，N=10000，双频FA=10KHz，其盲区在上面的讨论中已经很明确了，为了补回这些盲区，双频FB=10.003KHz，FB抽样时它的盲点则只分布在10.003KHz左右的（-1Hz～+1Hz），这样就可以补足FA在10KHz的盲区了。同理，在FB/2的左右（-0.5～+0.5）才是盲区，也可以补足FA在FA/2左右的盲区，这样一直分下去就可以得到结论，在［1Hz～10KHz］，FB可以完全补全FA的盲区，达到完全互补盲区的作用。

设想，系统先后进行FA，FB两次抽样率的抽样，各采值10000个点，在这20000个点里，选取最大值则为信号峰峰值。相当于信号在一个周期采20000个点，测幅的精度显然很高。

1.5 拓展频带到高频盲点分析

频谱分析［4］结论：可以肯定的讲，信号在1Hz～10KHz的任意频率的任意周期数值峰检都可以很准确的检出信号的峰值，其测量可以说是限制与ADC的测量精度和范围决定。

现在讨论信号的高频段，如果FA=10KHz，FB=10.003KHz，采样点数N=10000。先考虑FA，对区间进行定义，定义［1Hz～10KHz］为区间1，［10KHz～20KHz］为区间2，［20KHz～30KHz］为区间3，……，［（n-1）*10KHz，n*10KHz］为区间n。而对应的盲区则是每个区间边界处的［-1Hz～+1Hz］。

现在考虑一个问题，当n在增大的时候，FB的盲区会有什么样的变化。

随着n值的增大，FB的每个区间相对于FA的每个区间在逐渐往FA的下一个区间移动。FB的各个区间盲区也同时相对于FA的各个盲区在往FA的下一个盲区移动。这样相对的往后移动，总有一个时刻，FB第n个盲区会移到FA的第n+1个盲区上，或者发生重叠，这样就放生了盲区重叠，在这个重叠区域将无法采值到信号的一个周期从而无法判断信号峰值。当FB=10.003KHz时，n=3333时候，FB的盲区会和FA的盲区重叠，此时对应Fx约为33MHz处，所以该双频搭配起来的数值字峰值检波可以做到33MHz。当FB=10.002KHz，n=5000的时候会发生混叠，此时Fx为50MHz，该双频搭配的数字峰值检波可以做到50MHz。当FB=10.007KHz时，n=2857时候会出现盲区（第一个n=1428值跳过，未混叠），此时Fx约为28MHz，该双频搭配起来的数字峰值检波可以做到28MHz。

2 双频峰值检波性能论证

2.1 对于ADC的要求

双频数字峰值检测基于ADC的采样，所ADC的采样分辨率、模拟输入信号范围和采样速率都是限制双频峰检的指标。前两者大部ADC都可以很好的到达要求。最限制的就是ADC的采样率，当数字峰值检波要做到100MHz的时候，要求ADC的采样率也必须达到那么高。一般的ADC都具有内置的采样保持，如MAX114，虽然最高采样率是1MHz，但它通过内置的采样保持电路可以达到10MHz的测量能力（会有所衰减但不是很大）。所以要做到高频，要先考虑ADC的采样率。

2.2 采样时间上的要求

通过对这种采样方式的了解可以知道，如上面例子，峰检个需要采10000个值，所以双频峰检在时间上要2s，但对于一般系统的刷新速度上来说已经可以了。

峰检的时间由AD的采样率和要采信号的最低频限有关系，如系统最低频率只做到10Hz，采样率提示10倍或者采样点数N降低10倍，则只需0.2s时间，如系统最低频率做到100Hz则至需要0.02s。所以，理解这种峰值检波原理的设计员是完全可以设计出一个很低的采样时间t来适应自己的系统。而采样点数则是取决于采样速率和最低频率限的，在设计时选择合适搭配的双频来选择采样点数N。对于特殊的周期信号，如正、余弦、方波、三角波、锯齿波等峰值有正负且绝对值相等的周期信号，半周期就可以采到一个最大值，所以可以在采样时间上或采样低频的极限上都提高一倍。如上面说的例子，要么可以将采样时间降低一倍，要么可以将信号低频极限再往下降一倍。

2.3 对于采样信号的要求［5］

对于双频数字峰值检波来说，就是ADC对信号采样的过程，那么决定峰值检波性能的指标除了ADC，还有信号的本身的质量。如果采样过程中信号毛刺很大，或不规律的抖动，则信号的真实峰值将难以辨别。所以信号的质量是峰值准确度的一项有力保证。一般，ADC引入毛刺时并未开始信号的采样，所以，对采值几乎没有什么影响。但对于高频信号来说，信号的质量就一定时刻考虑了。

3 双频数值峰值检波的灵活变换与改进

3.1 双频的选择

双频的选择，如果采样信号的最低频限是固定的，则决定了采样点数N，也就决定着信号的采用精度。同时也决定了信号的盲区分布。所以设计者可以做很灵活的变换与改进。对于高速AD，可以适当的增大双频的取值，同时把信号的最低频极限往上提升，就可以得到很好的改进。

考虑双频与多频的采样，若找到一款双ADC，两路ADC可以同时采样，则在采样时间上最少可以减半，避免了之前的分前后采样。与之前的特殊周期信号采半个周期就可以确定信号峰值，可以把时间再减低一半。

如果很难找到适当的双频来达到我们的设计要求，系统可以采用多频方式，三频、四频等。可以有效的互补盲区。

3.2 频限的选择

如果系统在时间上有很大的要求，则要求设计者在频段和采样率上做好选择。考虑低频1Hz、10Hz、100Hz、1KHz、10KHz在时间上是截然不同的，如1Hz时对于特殊周期信号最短时间可以做到0.5s，但在10KHz时可以做到50us，所以在时间上面需要设计者灵活变化。

3.3 值得深究的问题

如果系统采样双频同时采样，即用两路同样的ADC（或内置两路完全独立的ADC），配合同样的采样时钟，搭配适当的双频进行采样时，则可以对信号不间断的采样，这种方法即使是非周期信号，系统也同样可以确定到信号的峰值（前提：峰值不是瞬时产生的，双频采样点数N足够大时可以采到那个峰值）。

3.4 数字有效值测量

有效值的测量原理基于公式：

数字处理均针对于离散的数字信号，所以将有效值公式转换为：

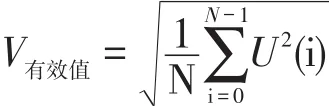
被测信号的瞬时幅度值经过A/D转换为数字信号后送入FPGA，利用FPGA内部的硬件资源依据公式计算平均值。

每个周期采样点数越多则精度越高，但计算速度会降低，所能够处理的信号带宽就越窄，因此要注意采样点数的选择。FPGA实现有效值测量的框图如下：

图3 FPGA有效值测量原理图

这种方案充分利用了FPGA的资源，实现简单，外部电路只要一个A/D转换芯片。经过实验表明，该方案测量精度较高，且能计算测量各种波形的有效值。但是由于要对被测信号的一个周期进行N点采样，所以大大降低了处理信号的带宽，被测信号的频率不能过高，能处理的带宽为模数采样率/N。该方案适用于频率比较低、频率基本不变的信号的有效值测量。

4 结语

对峰值，有效值测量方面，需要注意的是，对于规则波形，在测量其峰值或有效值时可以根据其中一个，然后利用它们的比例关系转换；但是对于不规则的波形，峰值测量就要用峰值测量的方法，有效值测量就要用有效值测量的方法。在实际应用中还有许多改进的方法。具体选择哪一种，需要对信号和系统的需求分析之后合理选择。

参考文献：

［1］刘睿强.FPGA应用技术及实践［M］.北京：北京理工大学出版社，2011：125-210.

［2］黄根春，陈小桥，等.电子设计教程［M］.北京：电子工业出版社，2007：51-65.

［3］Hern C C，McGillem C D.Target Motion Compensation by Spectrum Shifting in Synthetic Aperture Radar［J］.Aerospace and Electronic Systems，IEEE，1992，28（3）：895-901.

［4］黎全，陈卫，等.频谱搬移法的误差和噪声分析［J］.国防科技大学学报，2010，32（2）：152-154.

［5］高吉祥.数字电子技术［M］.北京：电子工业出版社，2010：54-105.

［6］任丽军，童子权，等.一种重复信号峰值检测的方法［J］.电测与仪表，2001，7（6）：24-26.