田间道路无人驾驶搬运车自动循迹行驶控制策略
2018-05-10孙红伟李云伍王小娟黄雪燕刘得雄
孙红伟, 李云伍, 王小娟, 黄雪燕, 刘得雄
(西南大学工程技术学院,重庆 400715)
农用物资在田间道路(特别是在丘陵山区)上的搬运耗费时间长、劳动强度大、工作效率低下,亟须自动行驶的搬运车来解放劳动力、提高工作效率[1-2]。自动循迹行驶是农业机械自动行驶的关键技术之一,近年来受到国内外学者的广泛研究,如张闻宇等提出了一种基于支持向量回归(support vector regression,简称SVR)逆向模型的拖拉机导航纯追踪控制方法[3];熊中刚等提出了一种基于免疫模糊PID控制[比例(proportion)-积分(integral)-微分(derivative)控制器,简称PID控制]的小型农业机械路径智能跟踪控制方法[4];韩科立等提出了基于最优控制的拖拉机路径跟踪方法[5]。
在已有的自动循迹控制方法中,PID控制及变形PID控制拥有结构简单、控制实时性高等特点[4,6-7]而受到广泛应用,但常规的PID控制是一种线性控制器,田间道路曲率变化大、起伏不平,在各种田间道路上常规PID控制系统难以均达到精确的自动循迹行驶控制。因此,提出一种基于分段式PID控制并预瞄前方路径曲率的自动循迹行驶控制方法。分段式PID能根据搬运车行驶的状态自适应调整PID控制系统的参数,有效改善常规PID控制的线性定常组合方式,提高搬运车自动循迹行驶的精度。预瞄控制能使搬运车根据前方路径的弯曲程度提前做出相应的转弯动作,以保证自动循迹行驶搬运车转向的平稳性。
1 数学模型的建立
试验用田间道路自动行驶搬运车是针对丘陵山区田间道路狭小、起伏、曲折等特征专门设计的(图1)。其主要参数如下:(1)质量:满载150 kg;(2)驱动:电动后轮驱动,功率 300 W;(3)转向:舵机驱动前轮转向;(4)前/后轮距:480 mm/510 mm;(5)轴距:1 100 mm;(6)前轮最大转角:30°。

1.1 搬运车转向几何模型
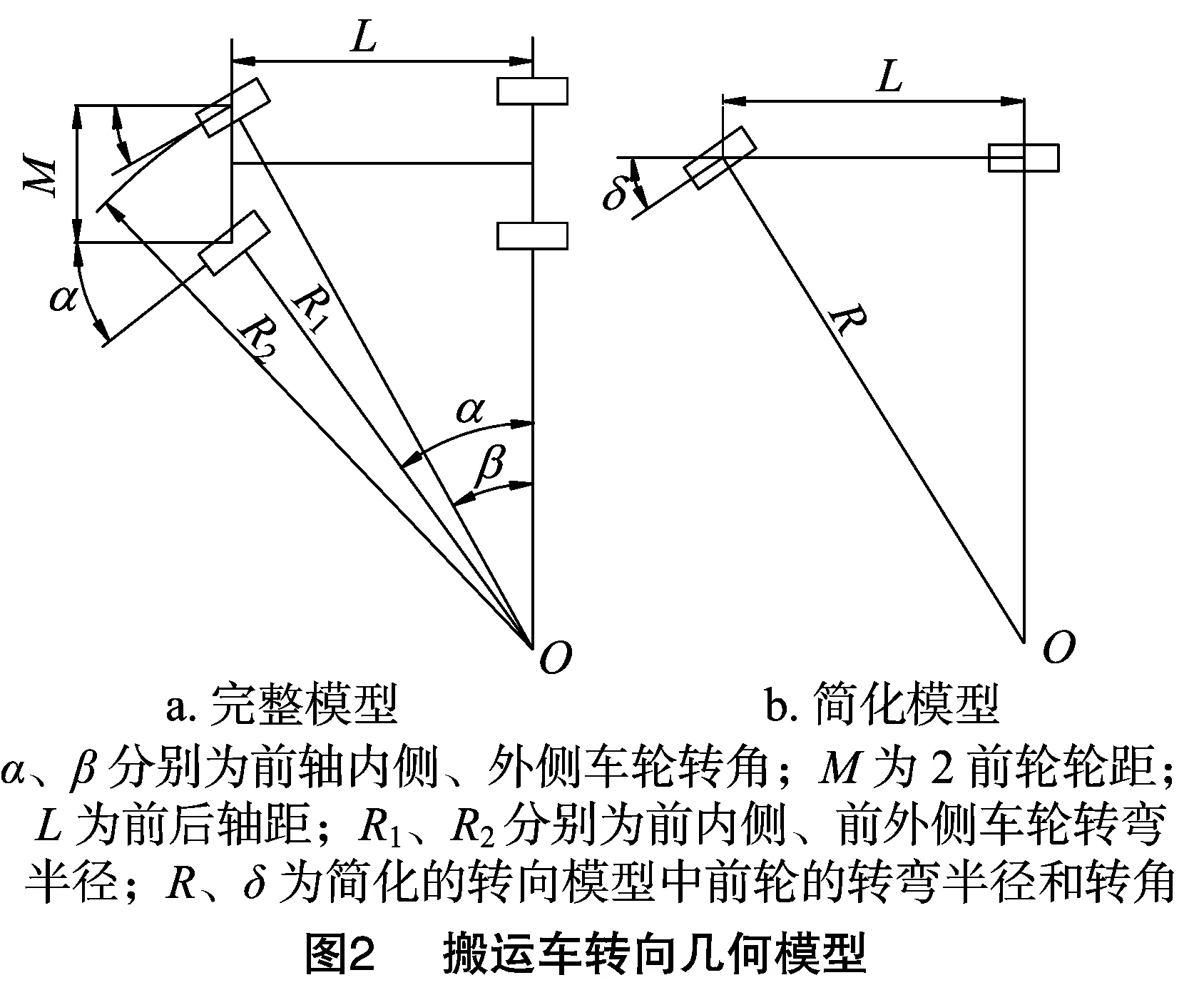
根据阿克曼转向原理,假设搬运车的每个车轮在任意时刻都是在做以侧向加速度为0的圆周运动或直线运动,且搬运车只做平行于地面的平面运动,得到搬运车的完整转向模型(图2-a)[8-9]。为计算简便,将搬运车4轮完整模型简化为中心线上布置前后轮的2轮模型,得到简化的转向模型(图2-b)。
根据搬运车的转向几何模型,得到式(1)、(2)、(3)的几何关系。
(1)
(2)
(3)
根据式(1)、(2)、(3)得到搬运车简化转向模型的转角与转弯半径的关系,如式(4)所示。
(4)
1.2 二维车路关系模型
根据简化的搬运车转向几何模型,再把道路以中心线为基准简化为一条曲线,以搬运车的前轮为研究对象,取离前轮中心最近的路径中心点为坐标原点O,以道路中心线的切线为x轴建立坐标系,构建二维车路关系模型(图3)。

对搬运车横向偏差求导得到横向偏差变化率,此变化率与搬运车相对道路中心线的航向角θ成正相关关系,此关系可以用式(5)表示。
(5)
式中:e(k)、e(k-1)分别表示k时刻与k-1时刻的横向偏差;T为2次偏差的时间间隔。
为使搬运车沿着曲率半径为ρ的道路行驶,根据式(4)可得搬运车的转角δ1,如式(6)所示。
(6)
2 控制策略
2.1 分段式PID控制的设计
在数字化控制中,常规的离散PID控制表达式如式(7)所示。
(7)
式中:kP、kI、kD分别为比例控制、积分控制、微分控制的常数;k表示积分总时间;T为1个控制周期的时间;e(j)、e(k)与e(k-1) 分别为j时刻、k时刻与k-1时刻的偏差值。
在PID控制策略中以搬运车的横向偏差e(k)作为比例环节的输入变量,一旦产生偏差立即产生控制作用,提高控制系统的响应速度;横向偏差e(k)的积分值作为积分环节的输入变量,以消除系统中存在的静差;由式(5)计算得到的航向角θ作为微分环节的输入变量,θ能反映e(k)的变化趋势,为控制系统引入1个有效的早期修正信号。
在常规离散PID控制中积分常数为固定值,当偏差较大时积分作用会造成大偏差的积累,以及造成较大的系统超调,这对搬运车循迹的精度影响很大。在分段式PID控制系统中,当目标值与实际反馈值的偏差达到切换阈值时,系统从现行的PID控制算法跳转到另外一个PID参数更合适的控制算法,使控制系统更加精确可靠[10]。田间道路曲折多变容易造成积分环节大偏差的积累,因此田间道路搬运车自动循迹行驶控制采用分段PID控制算法,以提高自动循迹行驶控制的精度。
以搬运车的横向偏差e(k)作为分段PID控制的输入变量,并以其值的域值范围把PID控制分为以下几段:
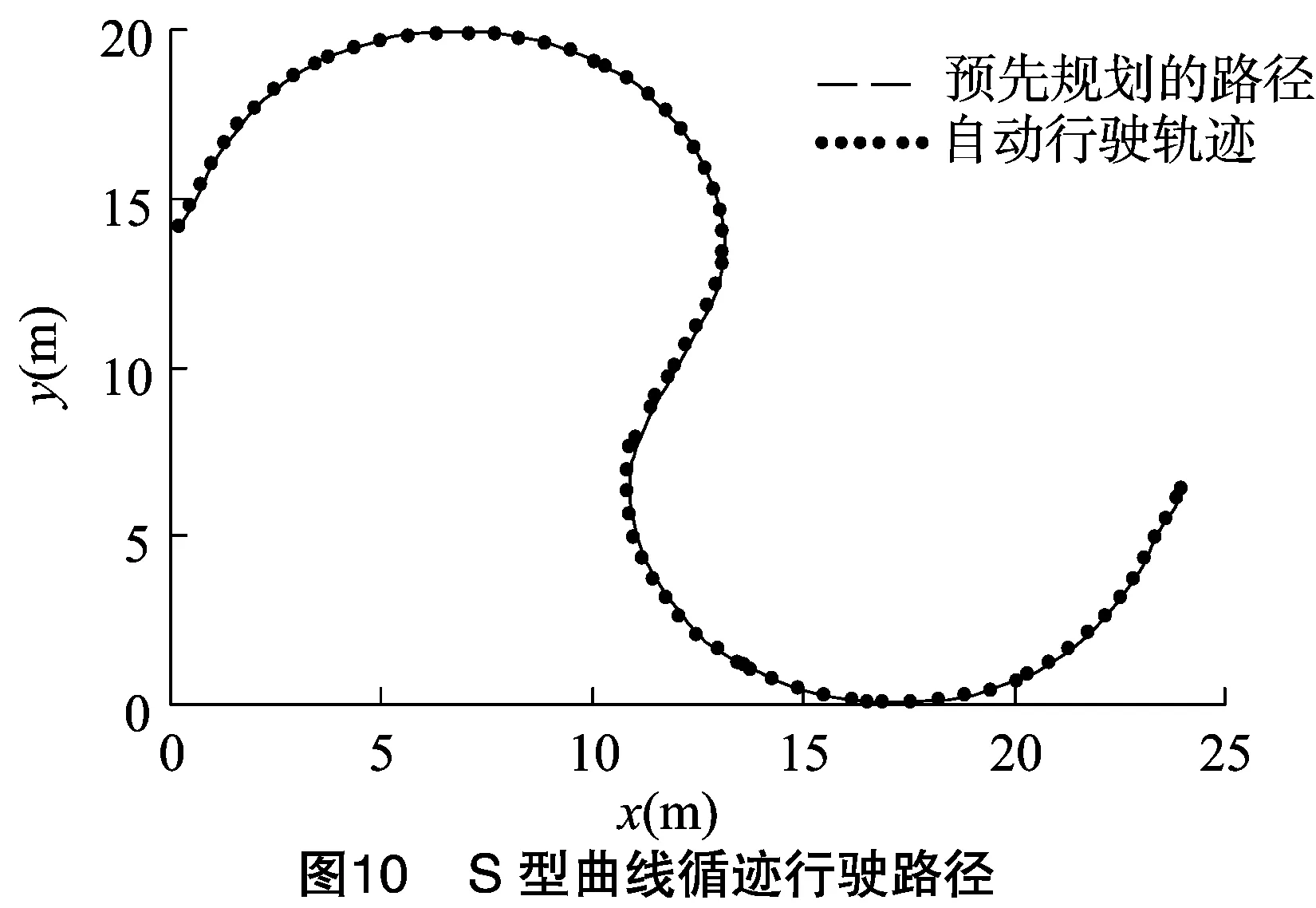
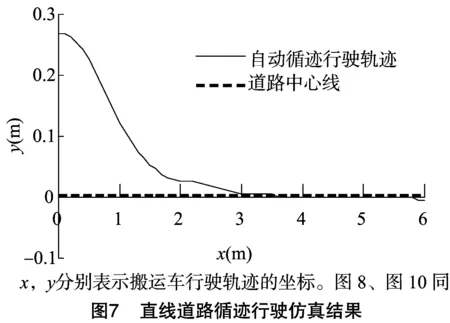
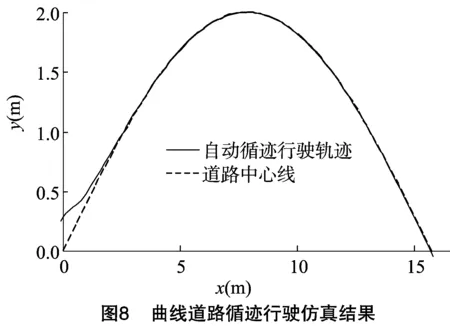
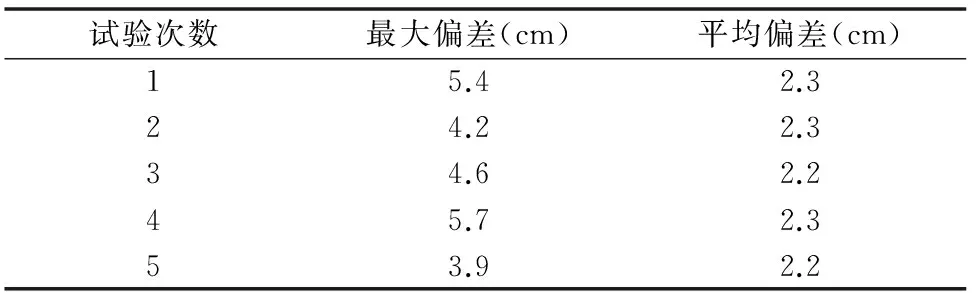
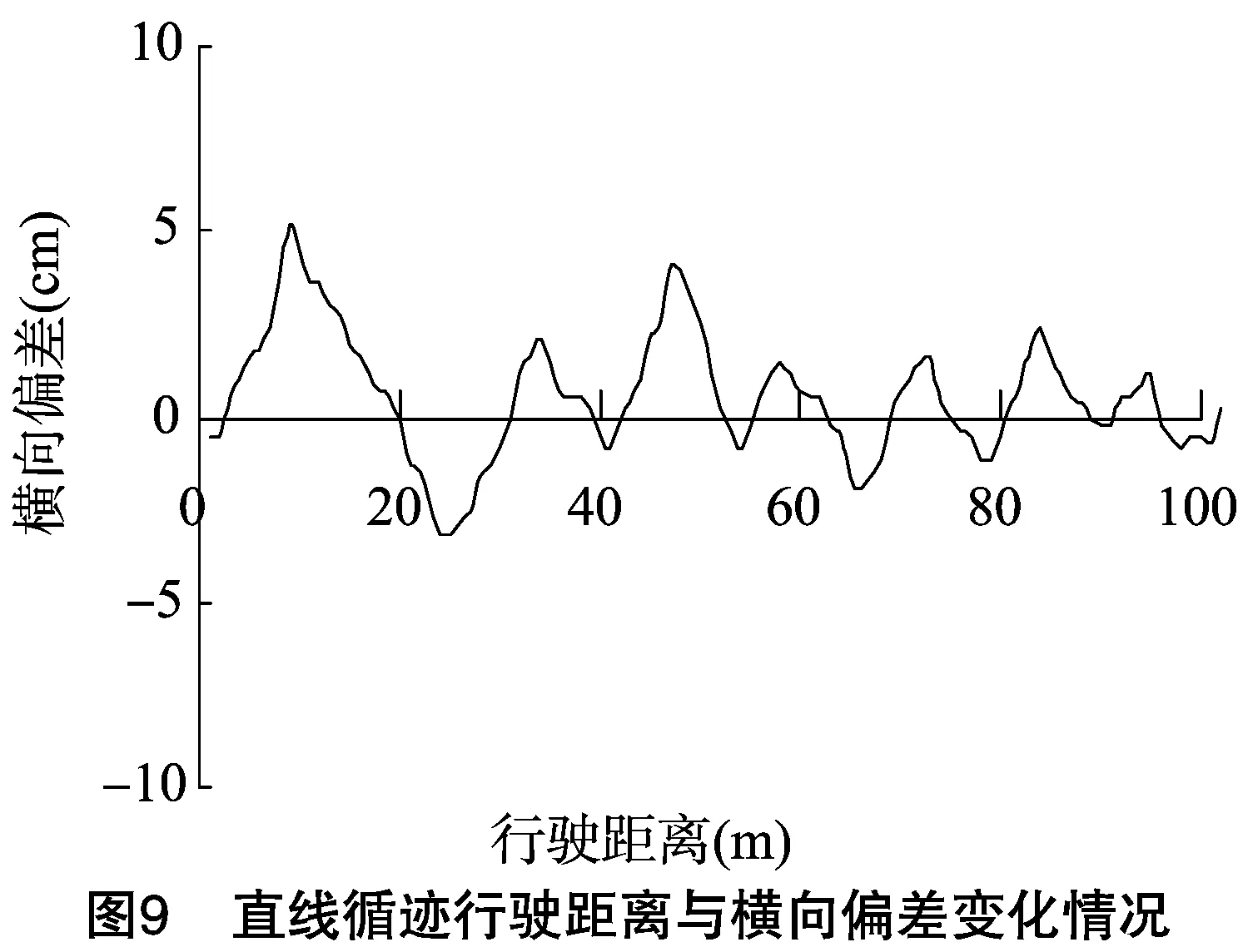
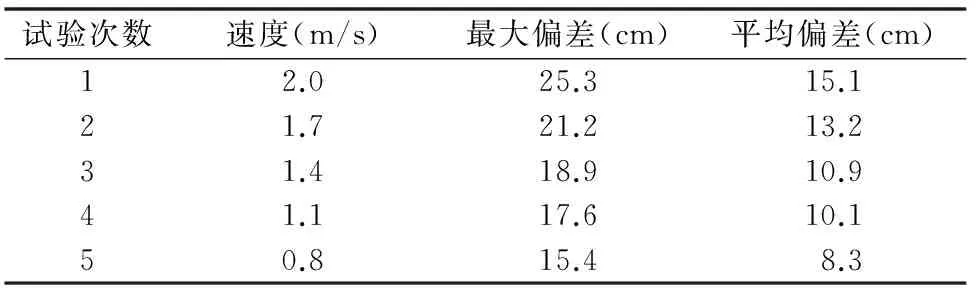
(1)当-e1 (2)当e1 (3)当e(k)>e2或e(k)<-e2时,搬运车的横向偏差较大,去除积分控制部分即令式(7)中的ki=0,只使用PD控制。这样既可以防止积分项积累大偏差而难以消除导致系统超调,又可以快速调节横向的偏差,使系统快速回到正常状态。 根据以上的分析,自动循迹的分段PID控制系统框架如图4所示。 自动循迹行驶的分段PID控制与常规PID控制的区别是加入了对偏差的选择判断,图4中积分作用I在不同的横向偏差e(t)下设定为不同的积分系数。由于进行了分段,被控对象状态发生变化时积分系数也会随之发生改变,使控制系统具有了一定的智能适应性。 前方路径弯曲程度是决定车辆转弯方向、转角大小及车速大小的重要因素[11-12],由式(6)可知,若前方一段路径的平均曲率为ρ,为了使搬运车沿着道路中心线行驶,搬运车的转角δ应为arcsin(Lρ),而分段式PID控制自动循迹行驶是一种针对横向偏差的实时控制,缺少对搬运车前方路径的预瞄性控制,这会导致搬运车在弯曲路径上自动循迹行驶时左右摆动幅度较大。因此,根据搬运车的运动参数选取搬运车前方一段路径的平均曲率进行预瞄控制,修正PID控制,从而使搬运车能精确地沿着弯曲路径自动循迹行驶,同时提高转向的平稳性。具体方法是在PID控制的基础上增加一个修正变量u(ρ),表达式如式(8)所示。 (8) 式中:u(ρ)是根据搬运车前方一段路径的平均曲率ρ得到的修正量,它正相关于搬运车的转角δ,关系可以用式(9)表示。 u(ρ)∝δarcsin(Lρ)。 (9) 搬运车分段PID控制并使用前方一段路径曲率预瞄修正的自动循迹行驶控制流程如图5所示。 根据上述的田间道路搬运车的实际结构参数和建立的转向模型、车路关系模型和控制策略,用Simulink建立仿真分析模型(图6)。 分别进行直线道路和曲线道路的自动循迹行驶仿真,验证提出的分段式PID控制并预瞄前方路径曲率的自动循迹行驶控制策略的可行性。定义较大的初始偏差为27 cm,仿真结果如图7、图8所示。 由图7、图8可知,即使在较大的初始偏差情况下,系统能迅速且平稳地作出相应的调整,且稳定后偏差很小。在直线道路循迹行驶仿真(图7)中,搬运车迅速平稳地向道路中心线靠近,当行驶到2.5 m时,27 cm的初始偏差已调节到只有2 cm,之后就处于稳定行驶状态,稳定后最大偏差为 0.4 cm。在曲线循迹行驶仿真(图8)中,搬运车也能够迅速平稳地向道路中心线靠近,行驶到2.8 m的时候,由27 cm的初始偏差调节到2 cm,随后搬运车循迹行驶只在路径曲率比较大的波峰或波谷处出现稍微的偏差,稳定后最大偏差为 1.3 cm。 采用图1所示的田间道路搬运车分别进行直线和曲线道路的自动循迹行驶试验,验证提出的分段式PID控制加预瞄修正的自动循迹行驶控制策略的有效性。试验中使用高精度的全球导航卫星系统(global navigation satellite system,简称GNSS)采集直线和曲线道路的路径位置信息并作平滑性处理后储存起来作为自动循迹行驶的跟踪线,自动循迹行驶过程中实时位置由高精度差分GNSS每0.1 s定位1次得到。 首先,用高精度GNSS定位系统采集处理得到1条直线路径的位置信息,起点和终点分别为A、B,并以A、B等2点构成的直线为x轴,将搬运车的前后轴中心线与x轴对正,航向角与x轴方向一致;然后启动搬运车,使搬运车以2 m/s的速度自动行驶,试验重复进行5次,结果如表1所示,其中试验中最大1次的路径跟踪偏差如图9所示。 表1直线循迹行驶试验结果 田间道路搬运车沿直线路径自动循迹行驶时,刚开始由于搬运车没有完全摆正、初始偏差值较大等原因使自动循迹行驶误差稍大,随着行驶距离增大误差越来越小;而且由于GNSS定位误差、转向系统机械误差等原因使偏差值始终围绕0 cm附近小幅度的波动。 结果表明,搬运车以2 m/s的速度自动循迹行驶时路径跟踪最大偏差为5.7 cm,平均偏差为2.3 cm,说明所设计的自动循迹行驶控制策略具有良好的控制性能。 同样先用高精度GNSS定位系统采集处理得到1条S形弧线路径的位置信息。采用5种不同车速共进行了5次曲线跟踪试验,试验结果如表2所示。其中,最大1次跟踪偏差的行驶路径如图10所示。 表2S型曲线循行驶迹试验结果 试验结果表明,搬运车以2 m/s的速度自动循迹行驶时路径跟踪的横向偏差最大,最大的偏差值仅为25.3 cm,平均偏差为15.1 cm,逐渐降低搬运车行驶速度,控制精度也得到相应提高,路径跟踪的横向偏差逐渐变小,满足田间道路搬运车自动循迹行驶的要求。 针对田间道路无人驾驶搬运车的自动循迹行驶控制问题,提出1种分段式PID控制同时预瞄前方路径曲率进行PID控制修正的控制策略。分段PID的控制方法能智能适应搬运车不同的横向偏差,提高了搬运车自动循迹行驶的控制精度。预瞄修正控制能使搬运车根据前方路径提前作出相应的转弯动作,提高了自动行驶搬运车转向的平稳性。 Simulink仿真分析结果表明,提出的分段PID加预瞄修正控制策略有很好的控制效果,无论是直线道路还是曲线道路,控制系统都可以对偏差作出迅速、平稳的响应,且系统稳定后偏差很小。 试验结果表明,在分段PID加预瞄修正控制策略下,搬运车直线自动循迹行驶平均偏差在2.3 cm以内,曲线自动循迹行驶平均偏差在15.1 cm以内,满足无人驾驶搬运车在田间道路上自动循迹行驶的要求。 参考文献: [1]冯启高,毛罕平. 我国农业机械化发展现状及对策[J]. 农机化研究,2010,32(2):245-248. [2]赵 映,肖宏儒,梅 松,等. 我国果园机械化生产现状与发展策略[J]. 中国农业大学学报,2017,22(6):116-127. [3]张闻宇,丁幼春,王雪玲,等. 基于SVR逆向模型的拖拉机导航纯追踪控制方法[J]. 农业机械学报,2016,47(1):29-36. [4]熊中刚,叶振环,贺 娟,等. 基于免疫模糊PID的小型农业机械路径智能跟踪控制[J]. 机器人,2015(2):212-223. [5]韩科立,朱忠祥,毛恩荣,等. 基于最优控制的导航拖拉机速度与航向联合控制方法[J]. 农业机械学报,2013,44(2):165-170. [6]He X,Cui T,Zhang D,et al. Development of an electric-driven control system for a precision planter based on a closed-loop PID algorithm[J]. Computers and Electronics in Agriculture,2017,136:184-192. [7]姜 勇. 基于双变量PID控制算法的地下智能铲运机自主导航技术研究[J]. 机械制造,2016,54(5):19-22. [8]沈法鹏,赵又群,赵洪光,等. 非线性轮胎侧向力对汽车转向稳定性的影响[J]. 中国机械工程,2015,26(1):135-139. [9]马 雷,贡士娇,李 斌,等. 四轮独立转向电动汽车转向控制方法[J]. 汽车工程,2015,37(9):1029-1034. [10]熊钰杉,徐 群. PID和Fuzzy控制相结合的分段复合控制[J]. 计算机仿真,2006,23(6):296-298. [11]陈焕明,郭孔辉. 基于航向角和位置偏差控制的驾驶员模型[J]. 农业机械学报,2013,44(10):36-40. [12]管 欣,王景武,高振海. 基于最优预瞄加速度决策的汽车自适应巡航控制系统[J]. 吉林大学学报(工学版),2004,34(2):189-193.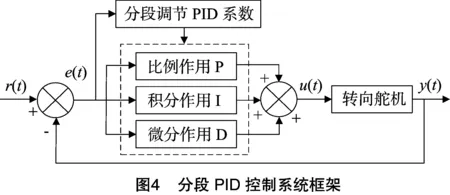
2.2 预瞄前方路径曲率修正PID控制

3 仿真分析
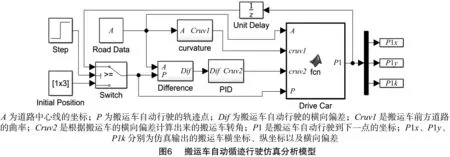
3.1 建立仿真分析模型
3.2 仿真结果分析
4 实车试验验证
4.1 直线路径试验
4.2 曲线路径试验
5 结论