基于改进扩散限制凝聚模型的点电极金属二维分形生长模拟

丁莉峰*，毛沛元，程军，王超, 王宇仙，邹子荣

（太原工业学院，山西 太原 030008）

金属电镀过程中形成的表面沉积层会呈现各种复杂形态，而枝晶为其中重要的一种，它对工业生产的特殊影响受到了研究者们的关注。枝晶具有形式上的对称性，可以满足实际应用中特殊的形态要求[1]；但与此同时，大量的枝晶不仅会影响电镀层的质量，甚至严重影响工业生产的正常进行，会引起电路短路，电极大量发热等问题[2-4]。因此，探索枝晶生长现象和生长规律，实现枝晶的可控生长成为目前的研究热点[5-6]。

许多学者对分形生长枝晶进行了研究。T.A.Witten等人提出的扩散限制凝聚(DLA)模型为研究电沉积产物形貌和枝晶问题提供了新的思路[7]。王桂峰等人制备且分析了具有分形结构的二维金属镍枝晶[8]；郑金玲等人探究了复合镀层表面分形维数与其显微硬度的关系[9]；熊晋等人通过计算机分形模拟，提出了电解锌的两种生长方式[10]；Keliang Wang等人通过研究电沉积锌的枝晶生长机理，提出了抑制枝晶生长的方案[11]。但目前分形枝晶的研究主要停留在实验方面，对其产生的原因以及理论研究不够完善。

本文通过计算机模拟，把影响金属沉积层枝晶形貌的外界条件[12-13](如沉积时间、外加电压、电解液温度、电解质浓度等)与程序参数相联系，解释其二维生长过程，最终实现非平衡条件下的可控生长，这对电化学的理论研究和应用都具有重要意义[14-16]。

1 分形生长的模拟方法

T.A.Witten和L.M.Sander在对大气中的煤尘、金属粉末和烟尘的扩散凝聚问题进行研究时，提出了DLA模型，其生长的特点主要表现为随机运动和边界变化。针对点生长，DLA模拟结果显示出粒子簇周围不同点的生长概率不同，比如粒子簇尖端附近的生长概率较大，而粒子簇的平凹处的生长概率较小。方格上单、双粒子集团周界点的生长概率分布显示[17]：单粒子四周沉积概率均为25%，而双粒子上下沉积概率均为28%，左右沉积概率均为22%。这就导致粒子优先在尖端集中生长，形成了常说的屏蔽效应[18]。

本文提出一种基于DLA的改进模型，模拟原理如下：在一个200 dpi × 200 dpi的阵列上，将粒子从半径为R的圆周上随机释放，粒子以随机运动的方式在平面上运动，通过改变包括粒子数、粒子运动步长和粒子漂移概率在内的计算机因素，粒子最终在点电极上沉积而形成粒子簇。

采用VB软件按照图1所示的程序框图进行编程，用MATLAB软件对模拟的形貌图进行分形维数的计算。程序设计由简单到复杂，在原有简单的程序上添加额外的粒子运动限制条件方程。其中，粒子的产生是随机的，封闭区域用圆方程进行限定，粒子的运动模拟了布朗运动等。

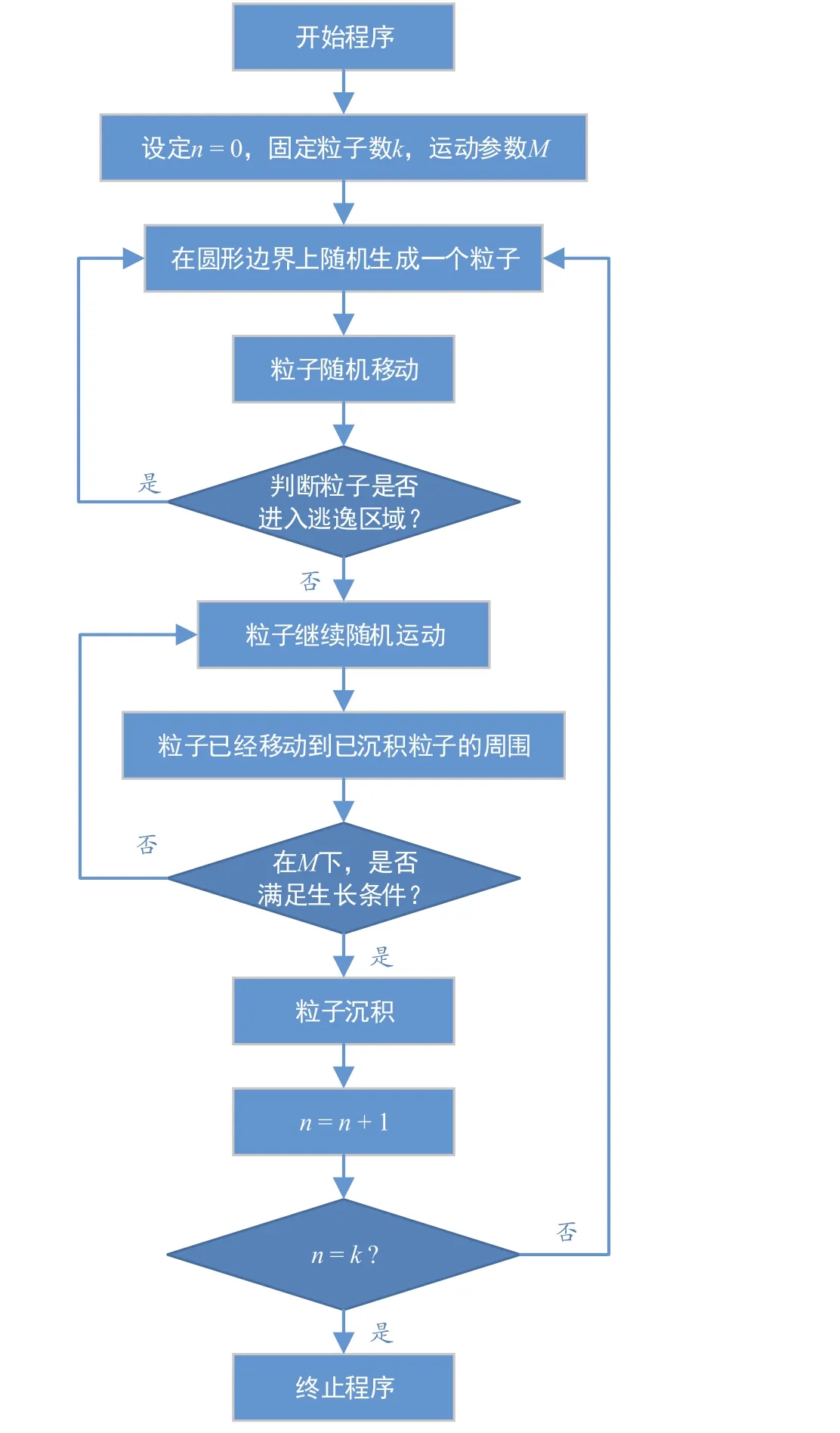
图1 模拟点电极分形生长的程序框图Figure 1 Flow chart for simulating the fractal growth on point electrode

2 模拟结果与分析

2.1 单一粒子数对分形图的影响

固定漂移概率为 1，探究单一粒子数对电极分形生长的影响。模拟过程中的粒子数表示溶液的浓度和电沉积时间，溶液的浓度越高或者沉积的时间越长，沉积的粒子数越多[19]。

从图2的模拟结果可知，粒子的生长方向是从圆心逐渐向外。图2a是粒子分形生长开始的状态，粒子随机运动生长为粒子簇[20-21]。由于不同方位的生长概率不同，随着粒子数增大，粒子开始呈枝干状生长，且枝干生长效应明显(见图2b)。随后在枝干生长的基础上开始聚集，呈大量粒子簇状(见图2c)。粒子数继续增多后，粒子枝干数开始增加，枝干之间凹槽增多(见图2d)。图2e中的粒子数进一步增多，开始体现屏蔽效应，粒子生长变得紧凑。图2f中明显呈现出屏蔽效应，粒子充满整个分形图。按计盒维数法[22-23]计算点电极形貌图的分形维数[24]，得到粒子数与分形维数的关系如图3所示。粒子数从1 000增长到10 000时，分形维数由1.38增大到1.80，增幅达到30.4%。粒子数大于10 000时，分形维数稳定在1.80 ～ 1.95之间，增幅仅为8.3%。这说明沉积层的屏蔽作用随着粒子数的增大而逐渐增大，粒子生长越来越密集。

图2 不同粒子数时的模拟分形结构Figure 2 Fractal structures simulated with different particle numbers

图3 粒子数与分形维数的关系Figure 3 Relationship between particle number and fractal dimension

2.2 固定漂移概率后粒子数对分形生长的影响

在实验中，电场对点电极分形生长的影响不能忽略。在模拟过程中，固定点电极与阳极的距离后，可以用漂移概率来表示电场强度的影响，漂移概率越大则电场强度越大。

图4 固定漂移概率后，粒子数对分形生长的影响Figure 4 Effect of particle number on fractal growth simulated with fixed drift probability

在2.1节的程序基础上，固定漂移概率为2来研究粒子数对点电极分形生长的影响，结果如图4所示。图4a显示了粒子一开始分形生长时的情况，粒子簇开始聚集。当粒子数增大时，粒子受到了固定漂移概率的影响，即粒子在定向的四周进行随机运动，粒子开始有向生长(见图4b)。对比图4c与图2d可以看出，粒子数增大到一定程度后，粒子簇开始集中，枝干开始有明显的偏向，且枝干粗大。图4d更明显体现出这种影响，即当粒子继续增大时，粒子开始在枝干四周运动，枝干间凹凸显著，粒子已经在固定的漂移方向集中生长。随后在固定漂移概率的影响下，枝干更加明显，粒子更趋向中心运动，模拟分形生长图(即图4e)更接近实际分形图。当粒子数再进一步增多，粒子不断在枝干上凝聚，生成粒子簇(见图4f)，体现出较强的屏蔽效应。

从5图可知，当粒子数小于20 000时，形貌图的分形维数急剧增大，增幅达到20%，说明此时粒子数对形貌图影响较大；当粒子数大于20 000时，在电场和粒子数的综合影响下，分形维数增幅缓慢，稳定在1.57 ～ 1.65之间。由此可知，随着粒子数的增加，分形生长的屏蔽效应体现得越来越明显，粒子更加容易密集生长，分形维数变化很小。这个现象在实验中体现为分形生长的局限性，与实验的电极边界具有一致性。

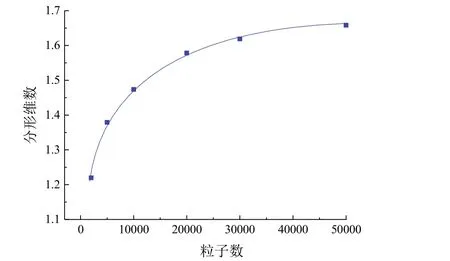
图5 固定漂移概率后，粒子数与分形维数的关系Figure 5 Relationship between particle number and fractal dimension at fixed drift probability

2.3 固定粒子数后运动步长对分形图的影响

上述模拟主要研究了粒子数对分形生长的影响，但实验中运动步长对分形生长的影响没有体现，因此对模型再进行改进。固定漂移概率为 1，改变粒子的运动步长，进而改变电沉积的速率，运动步长越大则沉积速率越快。

当运动步长为1时，粒子偏向于外层生长，表现出明显的屏蔽效应(见图6a)。当运动步长变为2时，粒子的沉积半径明显变小，生长紧密(见图6b)。当运动步长进一步增大到3时，粒子运动速度加快，因此粒子呈团簇状的概率更大，几乎所有粒子聚集到内层生长点，分形结构更加致密。

图6 固定粒子数后，运动步长对分形生长的影响Figure 6 Effect of motion step on fractal growth simulated with fixed particle number

将粒子数增大2倍后继续考察不同运动步长对分形图的影响。结果发现：当运动步长为1时，粒子簇达到了生长边界，布满整个区域，屏蔽作用明显(见图6d)；当运动步长为2时，粒子在内层生长点生长的概率增大，枝干渐粗(见图6e)；当运动步长变为3时，沉积层凹陷结构更加明显，粒子分布致密(见图6f )。

在真实的电沉积实验中，运动步长的增加体现为粒子扩散速度增加和沉积层晶粒生长速度的加快，也可代表实际体系中温度的升高。当可沉积的物质数量固定时，温度越高，反应越快，反应粒子的消耗也越快，实验持续的时间就越短。

由图7可知，相同粒子数时，随着粒子运动步长的增大，模拟图的分形维数逐渐降低。对比不同粒子数目下相同运动步长时的情况后发现，粒子数较多则模拟图的分形维数较大。粒子数为10 000时，分形维数集中在1.24 ～ 1.84之间，变化幅度为0.60；而粒子数为30 000时，分形维数集中在1.44 ～ 1.97之间，变化幅度为0.53。分析认为：运动步长对形貌图的影响较大，随着运动步长增大，粒子凝聚半径小，生长密集。

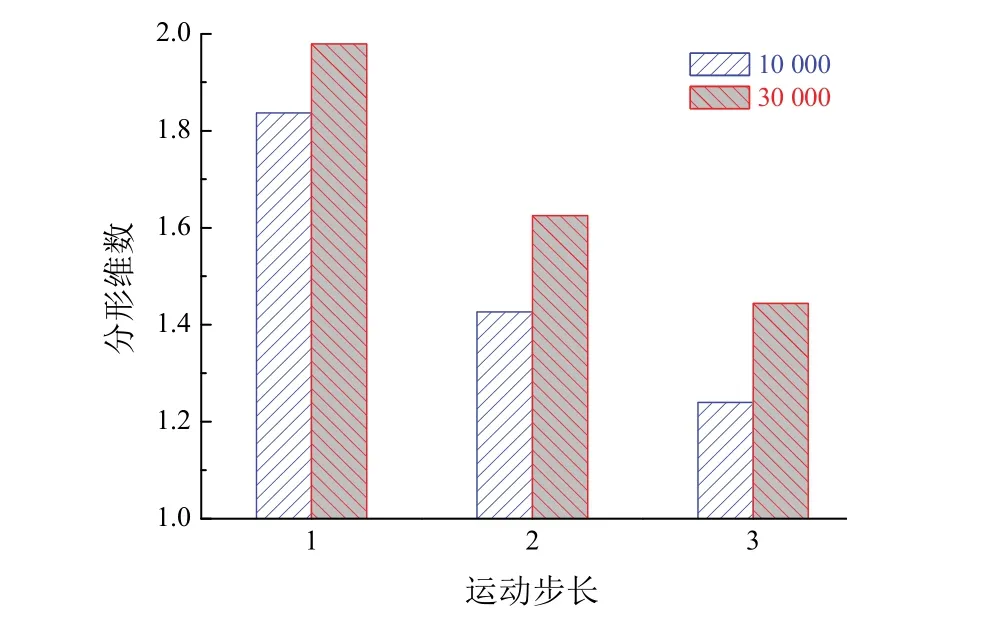
图7 不同粒子数下运动步长与分形维数的关系Figure 7 Relationship between motion step and fractal dimension at different particle numbers

2.4 固定漂移概率和粒子数后运动步长对分形图的影响

相比于2.3节，在固定粒子漂移概率为1和粒子数的基础上，探讨运动步长对点电极沉积的影响，如图8所示。

图8 固定漂移概率后，不同粒子数下运动步长对分形生长的影响Figure 8 Effect of motion step on fractal growth simulated at fixed drift probability with different particle numbers

从图8a−8c可以看出，在粒子数较小且漂移概率不变的情况下，运动步长较小时，粒子在枝干上凝聚生长，而随着运动步长变大，粒子运动加快，粒子进入内层凝聚点更加容易，粒子簇愈发致密，呈现出枝干饱和的形态，最终令粒子几乎全部集中于内层凝聚点。当粒子数增大后，粒子簇枝干粗大，局部分形特征显著，体现出粒子受到电场和步长两个因素的综合影响(见图8d)，而随着粒子运动步长变大，粒子凝聚半径同样变小，生长密集(见图8e)。当运动步长增大到一定程度，粒子开始向中心凝聚，枝干生长不明显(见图8f)。从本质上来看，图8a−8c和图8d−8f这两组图都反映了大致相同的规律，因为第二组实验的粒子数多，所以得到的沉积物多，分支也就更多，在分形图上看起来更大。

从图9可知，固定粒子定向漂移概率的情况下，当粒子数为10 000时，粒子形貌图的分形维数稳定在1.00 ～ 1.50之间；当粒子数为50 000时，粒子形貌图的分形维数稳定在1.31 ～ 1.71之间。另外，运动步长每增加1，粒子形貌图的分形维数大约减小0.2。分析认为，运动步长对形貌图的影响占主要地位，运动步长增大，粒子生长密集，粒子枝干生长不明显。

图9 固定漂移概率后，不同粒子数下运动步长与分形维数的关系Figure 9 Relationship between motion step and fractal dimension at fixed drift probability with different particle numbers

2.5 模拟和实验的分形图对比

图10a−10c为固定粒子漂移概率为2的情况下，不同粒子数时的分形模拟图。图10d−10f是利用简单的玻璃皿实验装置[8]，在25 °C，外加电压4 V，CuSO4浓度为1 mol/L，直径为1 mm的金属铜点阴极到高纯铜阳极环的距离为5 cm的条件下电沉积不同时间后，在直径为1 cm的圆片上得到的沉积物的放大照片。图10g−10i是对图10d−10f进行了图像处理后得到的分形图，用来计算分形维数。

图10 理论模拟分形图(a−c)与实验沉积物外观照片(d−f)及其分形维数计算图(g−i)的对比Figure 10 Comparison of the theoretically simulated fractal graphs (a–c) with the photos of experimental deposits and the graphs for calculating their fractal dimensions

对比3组图片后发现，模拟图与实验图比较吻合，且都存在明显的屏蔽作用。但是模拟图中分形生长较为密集，局部分形特征明显，实验图中分形生长的枝干则较为粗大、稀疏。从图11可知，模拟图和实验图的分形维数十分相近，均集中在1.24 ～ 1.65之间，但模拟图的分形维数略大。这种模拟结果与实验结果的不一致主要是由生长过程中的随机性所导致的。计算机随机生长是理想的随机状态，而实验时沉积物的随机生长受外界条件的影响较大，故两者在外型和分形维数上都存在一定的差异。

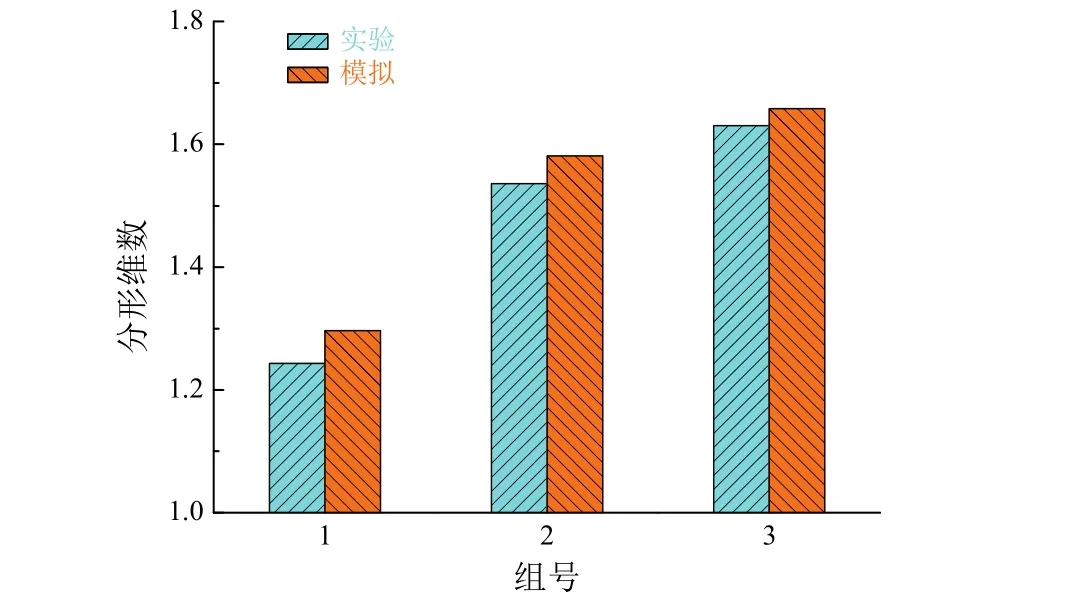
图11 模拟图与实验图的分形维数对比Figure 11 Comparison of fractal dimension between simulated and experimental graphs

3 结论

从粒子数、运动步长和粒子漂移概率三方面对传统DLA模型进行了改进，对金属点电极二维电沉积的产物形貌进行了计算机模拟研究，发现模拟的分形图与一定条件下实验得到的沉积产物的分形图较为吻合。所以，只要合理控制模拟时的参数，使其逼近实际电化学体系的实验条件，就可以获得与实际电沉积接近的分形图。模拟分形可以为进一步解释实际金属电沉积体系枝晶生长的原因提供理论依据。但是，建立的计算机模型与实际电沉积还是存在差距。比如实验过程中不可避免的蒸发现象，特别是在温度较高时更为突出，这一点在模拟中无法得到体现。另外，鉴于电沉积物具有多标度分形特征，对它的研究不能停留在宏观层面，应当在微观或者原子聚集的层面去研究分形生长形貌。

参考文献：

[1] 丛建臣, 倪培相, 孙军, 等.灰铸铁枝晶组织对机加工后石墨形态的影响[J].铸造技术, 2014, 35 (10): 2367-2370.

[2] 丁莉峰.电解制金属锰和高锰酸钾过程中的非线性动力学研究[D].重庆: 重庆大学, 2014.

[3] BRADY R M, BALL R C.Fractal growth of copper electrodeposits [J].Nature, 1984, 309 (5965): 225-229.

[4] HUANG D P, QI Y Y, BAI X T, et al.One-pot synthesis of dendritic gold nanostructures in aqueous solutions of quaternary ammonium cationic surfactants:effects of the head group and hydrocarbon chain length [J].ACS Applied Materials & interfaces, 2012, 4 (9): 4665-4671.

[5] PARANJPE A S.Sequence of morphological transitions in two-dimensional pattern growth from aqueous ascorbic acid solutions [J].Physical Review Letters,2002, 89 (7): 075504.

[6] 崔晓亚.三维分形银枝晶的可控制备及银浆应用研究[D].北京: 清华大学, 2015.

[7] WITTEN T A, SANDER L M.Diffusion-limited aggregation [J].Physical Review B (Condensed Matter), 1983, 27 (9): 5686-5697.

[8] 王桂峰, 黄因慧, 田宗军, 等.分形结构二维金属镍枝晶的制备与分析[J].电镀与涂饰, 2007, 26 (11): 1-7.

[9] 郑金玲, 胡小芳.镍−二氧化硅纳米复合镀层表面分形维数与显微硬度的关系[J].电镀与涂饰, 2011, 30 (9): 8-11.

[10] 熊晋, 徐献芝, 李芬, 等.电解锌分形生长的计算机模拟[J].电子技术, 2011, 38 (12): 23-24.

[11] WANG K L, PEI P C, MA Z, et al.Dendrite growth in the recharging process of zinc–air batteries [J].Journal of Materials Chemistry A, 2015, 3 (45):22648-22655.

[12] NAKOUZI E, SULTAN R.Fractal structures in two-metal electrodeposition systems II: Cu and Zn [J].Chaos: An Interdisciplinary Journal of Nonlinear Science, 2012, 22 (2): 023122.

[13] 张皓东, 谢刚, 李荣兴, 等.金属锌电沉积过程的分形研究[J].化学研究, 2005, 16 (1): 52-54.

[14] 田宗军, 王桂峰, 黄因慧, 等.金属镍电沉积中枝晶的分形生长[J].中国有色金属学报, 2009, 19 (1): 167-173.

[15] EGGERSDORFER M L, KADAU D, HERRMANN H J, et al.Multiparticle sintering dynamics: from fractal-like aggregates to compact structures [J].Langmuir, 2011, 27 (10): 6358-6367.

[16] JIANG X B, WANG J K, HOU B H, et al.Progress in the application of fractal porous media theory to property analysis and process simulation in melt crystallization [J].Industrial & Engineering Chemistry Research, 2013, 52 (45): 15685-15701.

[17] 刁先锋.分形生长的计算机模拟研究[D].开封: 河南大学, 2008.

[18] SHAIKH Y H, KHAN A R, PATHAN J M, et al.Fractal pattern growth simulation in electrodeposition and study of the shifting of center of mass [J].Chaos,Solitons & Fractals, 2009, 42 (5): 2796-2803.

[19] 田宗军, 王桂峰, 黄因慧, 等.喷射电沉积中镍枝晶分形生长的数值模拟[J].机械工程材料, 2009, 33 (9): 41-43, 100.

[20] 张皓东, 谢刚, 李荣兴, 等.平行板阴极金属电沉积过程枝晶二维生长的计算机模拟[J].昆明理工大学学报(理工版), 2005, 30 (3): 31-34.

[21] MATSUSHITA M, HAYAKAWA Y, SAWADA Y.Fractal structure and cluster statistics of zinc-metal trees deposited on a line electrode [J].Physical Review A, 1985, 32 (6): 3814-3816.

[22] LI J, DU Q, SUN C X.An improved box-counting method for image fractal dimension estimation [J].Pattern Recognition, 2009, 42 (11): 2460-2469.

[23] 吴成宝, 田巨, 刘传生, 等.镀层表面轮廓曲线分形维数计算方法的评价[J].电镀与涂饰, 2017, 36 (8): 403-408.

[24] FERNÁNDEZ-MARTÍNEZ M, SÁNCHEZ-GRANERO M A.A new fractal dimension for curves based on fractal structures [J].Topology and its Applications, 2016, 203: 108-124.