应用ANSYS软件分析温度对测量半球形薄壁零件尺寸的影响

2018-05-09上海市计量测试技术研究院

上海计量测试 2018年2期

/ 上海市计量测试技术研究院

0 引言

温度变化会导致金属零件产生尺寸、形状上的变化，因此对温度分布的分析及温度对器件在生产加工中所产生的影响进行研究是至关重要的课题[1-3]。同时，温度也是对精密测量产生影响的几个关键因素之一[4-6]。而如果能在测量开始前对待测零件受温度影响所产生的变化进行分析，对器件形变的结果有预先的判断，则可以提前制定合理的测量方法、提高测量准确性。

对于半球形薄壁类零件，一般采用数字式万能显微镜、光学投影仪或图像扫描技术三种方法测量其轮廓参数。对其受温度影响所产生误差进行分析传统上主要通过热致误差公式进行计算分析[7,8]，这种方法是通过对材料受热形变进行计算得到分析结果。这种分析方式由于计算量大，且无法对模型进行整体分析，所以现在已较少被使用。而使用有限元方法对零件进行温度场分析及形变分析已经成为主流的方法[3,9-12]。通过使用有限元模型进行分析可以全面、准确地获得零件受温度变化的仿真结果，简化了分析过程，更便于工程人员进行使用。

1 半球形薄壁零件有限元模型建立及边界条件设定

使用三维绘图软件Solidworks对某类半球形薄壁零件进行三维图绘制。球体半径为10 mm，厚度为0.2 mm。由于半球体薄壁零件属于轴对称零件，在进行有限元分析时，为了简化分析过程，只选取零件沿轴对称后的一半进行分析即可。所绘制的半球形薄壁零件的三维图如图1所示。

图1 半球形薄壁零件三维图

在ANSYS Workbench中建立静态结构分析项目，并将所绘制的三维模型导入Geometry中，设置模型材料类型为铝合金（Aluminum Alloy）。并对模型进行边界条件设定，在模型的底边设置固定约束（Fixed Support）A，模拟零件被固定限位的情况；在模型被切割表面设置无摩擦约束（Frictionless Support）B，以还原模型被简化前的状况[13]。边界条件设置结果如图2所示。

图2 边界条件设置

同时设置热力工况（Thermal Condition）为梯度降温方式，以模拟零件由高温转变为接近环境温度（22 ℃）的变化过程。热力工况设置结果如图3所示。

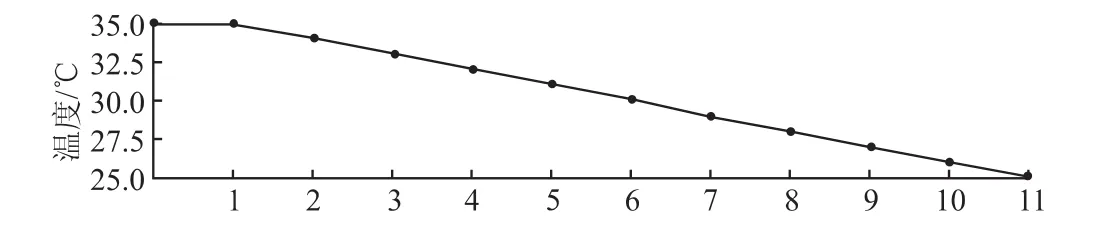
图3 热力工况设置

在模型中添加半球形薄壁零件切面上边缘边线为一段路径（Path），将求解在此路径下零件的受热形变情况。路径设置图如图4所示，路径起点为1，终止点为2。

图4 路径设置

2 零件受热形变求解

将总体形变和路径在不同温度下的形变设置为求解项，并对模型进行网格划分，之后利用ANSYS软件的求解功能，对所设置的求解项进行求解。

模型在35 ℃条件下的总体形变云图及路径形变图如图5所示。

图5 模型形变云图

3 曲线拟合及数据分析

对路径形变曲线的值进行提取，在路径曲线上选取129个点，分别获得每个点所对应的形变量。将软件计算得到的形变量与曲线长度对应关系的数据输入Matlab中，绘制形变量与球体半径对应关系的曲线图。绘制得到的曲线图如图6所示。

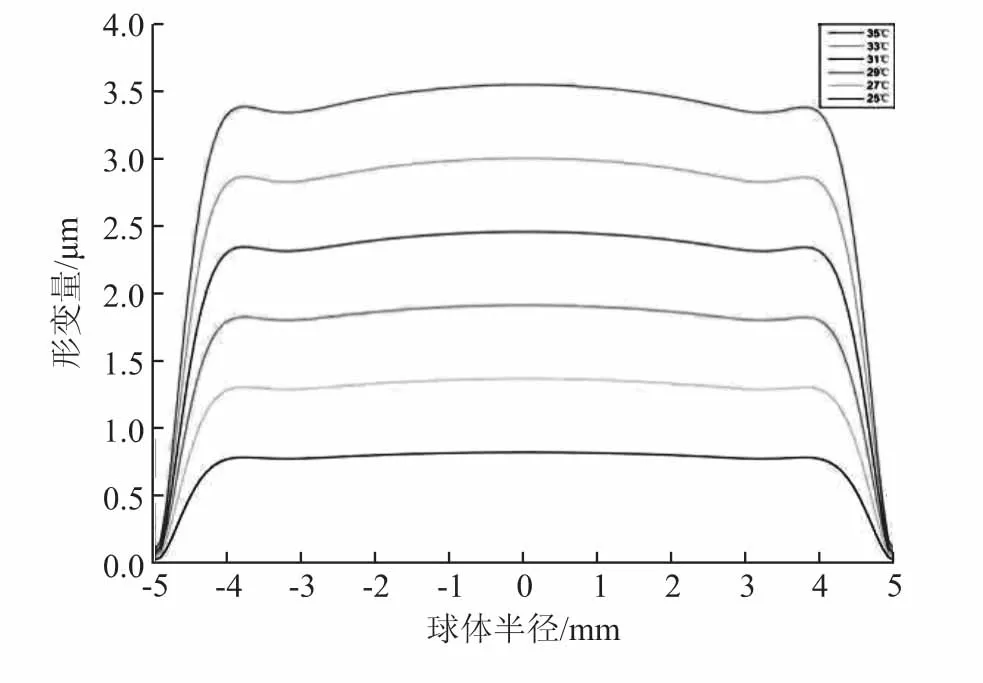
图6 形变曲线

不同温度下，路径最大形变量与最小形变量的数值如表1所示。

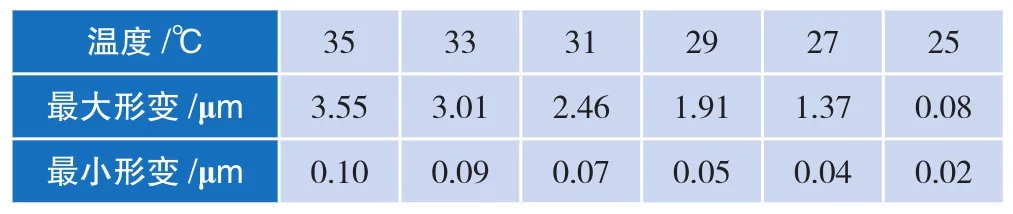
表1 不同温度下的形变量

由形变曲线图及不同温度下的形变量表可以看出：

（1）由于零件底端被固定，受到底端限位作用和材料在轴向上的非线性分布，所以零件受温度影响的形变也是非线性的。

（2）温度值越高，零件形变的最大值与最小值的差值越明显，因此在进行测量时应避免在零件高温时进行测量，其测量的不均匀性越明显。

（3）零件在固定端的形变受温度的影响最小，因此在进行测量时可以考虑在接近零件固定端进行测量，这样的测量结果受温度的影响相对较小。

（4）半球形薄壁零件在受固定约束及温度变化两种条件的影响下，其形变量在以球心对称的0.8倍半径下达到均匀的较大值。在这一范围内的形变量产生了明显的突变。

4 结语

本文通过对半球形薄壁类零件在不同温度下的形变情况进行了有限元分析。通过对软件模拟得到的路径形变数值进行曲线拟合绘制，得到了形变图。通过对不同温度下路径形变曲线的对比，得出了零件形变的基本规律。通过使用ANSYS对半球形薄壁零件在不同温度下形变进行有限元分析，可以明确半球薄壁类零件的形变规律,为改进合理的测量方法及进行精确测量提供理论依据。

[1]马泳涛，张建立，李钝，等. 均匀温度场下零件热形变行为的研究[J]. 矿山机械，2010，38（10）：31-34.

[2]徐振宇，李大勇，马旭梁，等. 球铁炉前热分析-共晶膨胀双曲线精密测量方法[J]. 机械工程学报，2016，52（06）：65-71.

[3]解维华，张博明，杜善义. 重复使用飞行器金属热防护系统的有限元分析与设计[J]. 航空学报，2006，（04）：650-656.

[4]陈俊华，陈俊龙，童森林. 卡尺使用中容易疏忽的两项测量误差[J]. 工具技术，2002，（08）：64-65.

[5]刘永谦. 如何减少温度对长度测量的影响[J]. 中国计量，2014，（01）：91.

[6]曾庆锋. 加油机计量检定中温度对测量误差的影响分析[J]. 中国设备工程，2017，（11）：52-53.

[7]刘素英，张贵武，石晶. 温度变化对工件加工与测量精度的影响[J]. 汽车技术，1995，（03）：44-47.

[8]殷海荣，章春香，刘立营. 差热分析在玻璃学研究中的应用[J].陶瓷，2008，（06）：14-18.

[9]王伟，高跃飞. ANSYS二次开发在火炮身管温度场计算中的应用[J]. 机械工程与自动化，2014，（04）：61-63.

[10]颜超英，刘江南，刘艳萍，等. 基于热形变分析的液体静压电主轴系统参数优化[J]. 机械强度，2017，39（01）：154-159.

[11]程刚，陈方斌，袁孝民，等. 基于Ansys的光学器件热形变仿真与分析[J]. 应用光学，2008，（05）：697-700.

[12]高慧莲，朱敏波，宋东升. 典型轴类零件的热形变规律[J]. 机械设计与研究，2009，25（01）：71-72.