隧道口声屏障受列车风荷载影响的数值计算分析

余海洪， 叶葵葵

(1.中铁四川生态城投资有限公司，四川眉山 620500; 2.中铁二院工程集团有限责任公司，四川成都 610031)

目前对声屏障的研究大多停留在普通路基和桥梁段声屏障上，对隧道口声屏障研究的公开资料较少。当列车进出隧道时，列车周围的空气处在复杂的三维紊流流动中，隧道口声屏障会受到这种三维效应的影响，使使隧道口声屏障上承受了比普通路基、桥梁段声屏障更加复杂的动态列车风荷载[4]。因此，对隧道口声屏障进行研究是很有必要的。

1 流场数值计算模型

1.1 几何模型

高速列车通过隧道引起的空气流动是三维、非稳态、可压缩的湍流流动。由于模拟计算车速取250 km/h及以上，并且隧道内的空气受到隧道壁的限制，空气流动需要当作可压缩处理。对粘性、可压缩的基本方程进行雷诺时均化，并附加κ-ε方程湍流模型来求解列车高速通过隧道口声屏障区域时，隧道口声屏障表面上受到的列车风荷载。

列车模型采用8车编组，每节车长都是25 m，车宽3.36 m，车高3.86 m，列车的最大横截面面积为12.257 m2。考虑到计算机的硬件条件和计算时间，不考虑列车外部复杂构造，如车门、受电弓等，这些复杂结构对整体列车风荷载影响甚微。列车计算简化模型如图1所示。

铁路线路考虑为双线，线间距为5 m，隧道进口和出口附近在纵向都布置了长50 m、高4 m的直立式声屏障，声屏障离近侧线路中心线距离L分别取3.5 m、4.25 m、5 m。图2为列车高速驶过隧道口声屏障区域时的平面布置示意图。由于声屏障实际构造相对较复杂，在模拟时对它做了一些简化，把它简化成具有一定厚度的平面板，不考虑底板、基础等结构。

图2 平面布置示意(单位：m)

隧道断面模型如图3所示，列车底部距离地面0.376 m，复线线路中线距离为5 m，隧道阻塞比为0.122。

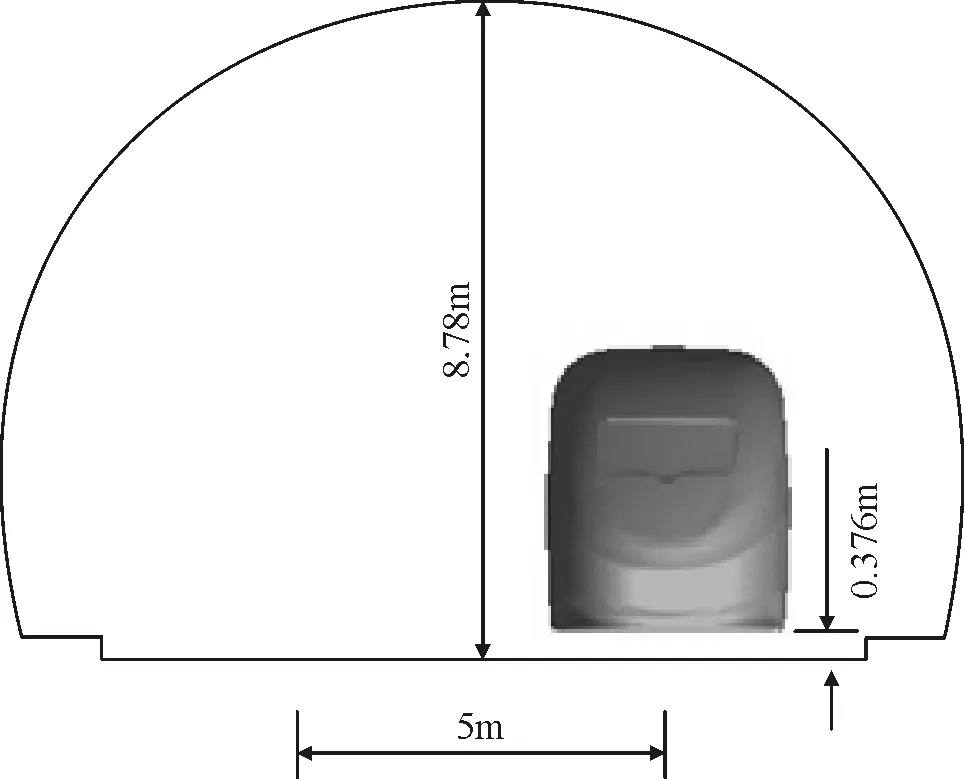
图3 隧道横断面

1.2 计算区域

在建立流场计算区域时，考虑到流场的充分发展以及气流的绕流影响，计算区域尺寸的取值应当足够大。理论上流场区域应该趋于无穷大，但在模拟时只能通过有限空间来近似处理这个无限流场，模拟的流场区域越大，网格数量将会越多，从而导致计算速度降低。因此在确保满足精度的前提下可以适当提高求解速度，通过对多个不同尺寸的流场区域进行计算分析比较，最后选取了如图4示的流场计算区域，列车离隧道进口为100 m[5]。

1.3 边界条件及网格划分

通过计算流体软件FLUENT中的网格滑移方法来处理列车与隧道及声屏障之间的相对移动，计算区域由移动区域和固定区域两部分组成，其中移动区域的网格以列车行驶速度滑移，固定区域的网格保持不动，移动区域和固定区域的信息通过交界面来传递，图5为流场分区示意图。

图4 计算区域示意

图5 流场分区示意

如图5示：外部流场A、B、C、D设定为压力出口边界条件，网格信息交界面E、F、G设定为滑移边界条件，交界面用“interface对”来解决移动区域和静止区域数据交换。隧道壁面、地面和隧道进出口面I、H，以及车体和声屏障等都设定为无滑移固定壁面边界条件。

通过ICEM CFD网格划分工具对整个计算模型分区域进行网格划分，固定区域使用结构化网格划分，移动区域使用结构化网格和非结构化网格相结合的混合网格划分。

2 隧道口声屏障表面上受到的列车风荷载的计算分析

为研究列车单车高速驶过隧道口声屏障区域时，声屏障表面受到列车风荷载的影响，本文计算了不同列车速度、不同隧道长度和声屏障距线路中心线不同距离等情况下，隧道进、出口声屏障纵向方向上0 m、5 m、10 m、20 m、30 m、40 m、50 m处受到列车风荷载的大小，总结出了隧道口声屏障表面上受到的列车风荷载的分布规律[6-7]。测点布置如图6、图7示。

图6 声屏障上纵向测点位置

图7 声屏障上竖向测点位置

2.1 隧道长度对声屏障上列车风荷载的影响

为了研究隧道长度对设置在隧道口声屏障上受到的列车脉动风荷载的影响，取声屏障距线路中心线距离为3.5 m，列车单车以时速250 km分别驶过长为1 443 m和786 m的隧道情况进行计算机仿真模拟，隧道出口声屏障内侧同一高度处(测点c)不同纵向位置监测点处头波波峰和头波波谷差值对比统计如表1所示。表1中头波波峰差值和头波波谷差值都是用786 m长的隧道计算结果减1 443 m长的隧道计算结果。

表1 不同纵向监测点处头波波峰和头波波谷差值对比

注：表中△P指△P1和△P2中的最大值，P指隧道长度为786 m时头波波峰或头波波谷压力值。

由表1可知：在除隧道长度不一样而其它条件都相同的情况下，设置在长度为1 443 m和786 m的隧道出口处声屏障内侧同一高度处不同纵向位置监测点处头波波峰和头波波谷差值都很小，保持在5 %的范围内，所以，设置在隧道口的声屏障表面上受到的列车风荷载受隧道长度的影响很小。因此，本文在后续计算分析中只考虑了隧道长度为786 m的情况。

2.2 声屏障竖向高度上的列车风荷载的分布

为进一步分析设置在隧道口的声屏障在竖向高度上的列车风荷载分布规律，我们选取了时速为300 km的列车通过设置在786 m长的隧道进、出口外的距线路中心距为3.5 m的声屏障的情况下的计算结果。从声屏障的底部竖直向上在其内侧均匀取6个监测点，测点的布置见图6、图7。由于列车通过隧道口声屏障时，头波波峰、波谷值相对于尾波波峰和波谷幅值变化趋势明显，更具有代表性，所以在计算中只对头波波峰和波谷的计算值做了分析。相关的对比图见图8～图11。

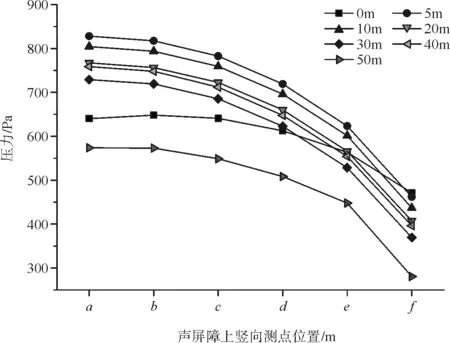
图8 隧道进口声屏障测点头波波峰值竖向分布

图9 隧道进口声屏障测点头波波谷值竖向分布

从图8和图9可见，隧道进口外声屏障测点头波波峰值、波谷值竖向分布都是沿着声屏障高度向上幅值减小，声屏障中间测点比始(0 m)、末(50 m)测点幅值减小得要快些，幅值相差大些。这是由于下部要比其顶部封闭性要好些，气流在其下部的流动会受到更多的限制，因此声屏障下部结构表面受到的列车风荷载幅值要比顶部大些；离隧道进口0 m和50 m处的声屏障相对于靠近其中间部分的受到限制要少些，所以离隧道口0 m和50 m处的声屏障的测点上的列车风荷载幅值相对较小，同时由于离隧道进口很近，会受到隧道口复杂三维流场的影响，造成了隧道口(0 m)处测点压力变化相对较复杂。

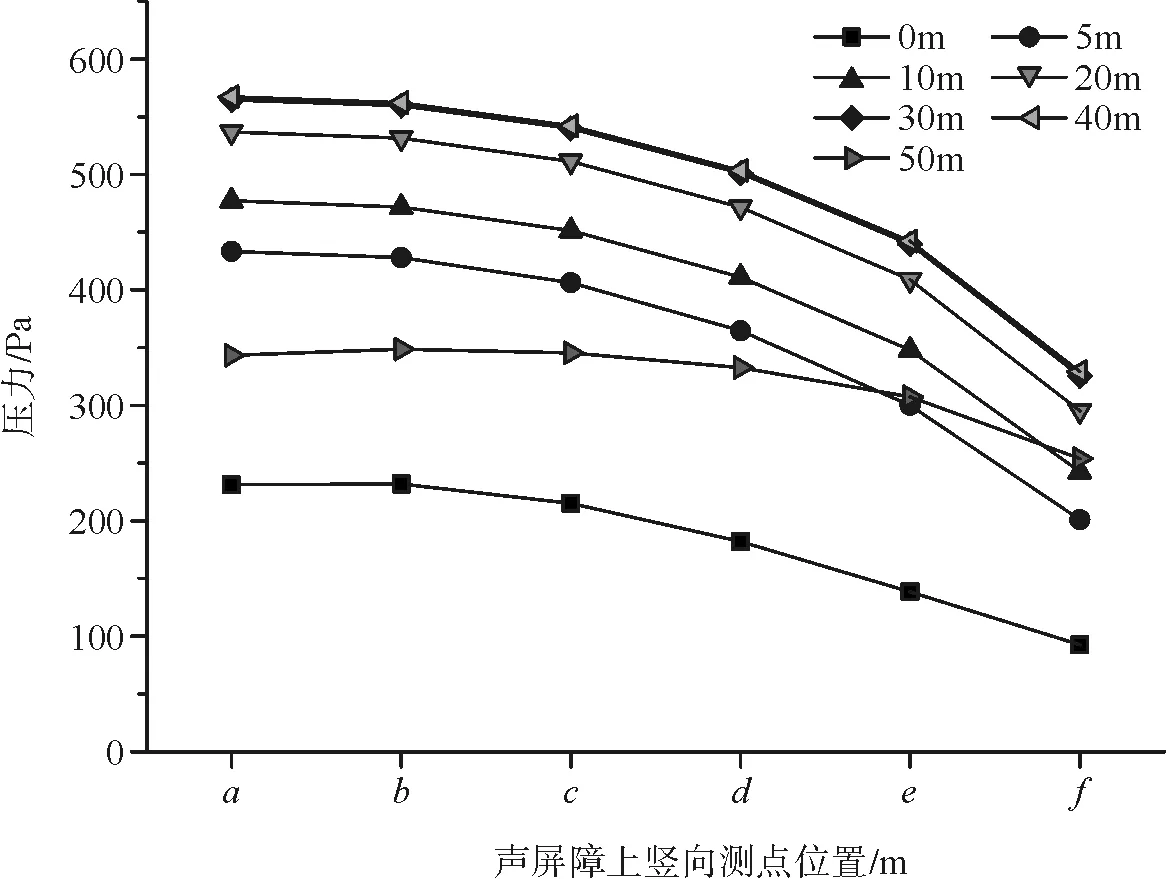
图10 隧道出口声屏障测点头波波峰值竖向分布

图11 隧道出口声屏障测点头波波谷值竖向分布

由图10、图11可以看出，隧道出口外声屏障竖向高度上列车风荷载的分布规律和隧道进口外声屏障基本一致。对比图8～图11，可以发现，在离隧道口相同距离时，隧道出口声屏障上的压力幅值要比隧道进口的要小。

2.3 列车风荷载沿着声屏障纵向上的分布

为研究声屏障上受到列车脉动风压幅值沿着声屏障纵向方向上的变化规律，取声屏障距线路中心为3.5 m时，列车分别以250 km/h、300 km/h、350 km/h的速度通过设置在隧道口的声屏障区域，声屏障面板竖向上中间位置(编号为c)的一纵行测点的计算结果进行分析。图12、图13为测点压力波幅值与纵向测点的关系曲线。

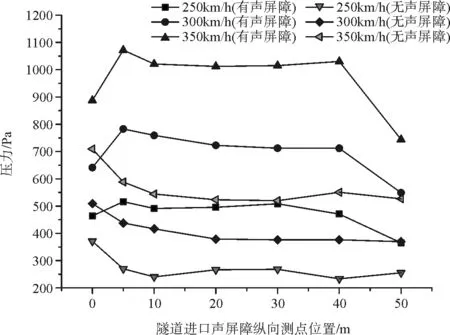
图12 隧道进口声屏障纵向测点头波波峰值压力变化

图13 隧道进口声屏障纵向测点头波波谷值压力变化

由图12和图13可知：离隧道进口5 m范围内，声屏障受隧道口三维效应的影响较大；离隧道进口5～20 m范围内受三维效应影响相对小很多；离隧道进口20 m以外，声屏障就不再受到三维效应的影响。声屏障始(0 m)、末(50 m)端由于密闭性没有中间部分的好，所以会在声屏障始(0 m)、末(50 m)端造成声屏障上受到的压力会幅值突然减小。隧道进口三维效应的影响范围和列车运行速度关系不大，但影响强度随列车运行速度的增加而增加；在离隧道进口相同位置处，设不设置声屏障对隧道进口外三维效应的影响范围几乎没有影响。

由图14、图15可知：越靠近隧道出口，声屏障受隧道出口三维效应的影响强度越大，列车速度越快，影响范围也就越大，隧道出口5 m范围内，声屏障上的脉动风压受影响强度要比隧道出口5 m范围外的大的多。在离隧道出口相同位置处，设不设置声屏障对隧道进口外三维效应的影响范围也几乎没有影响。

图14 隧道出口声屏障纵向测点头波波峰值压力变化

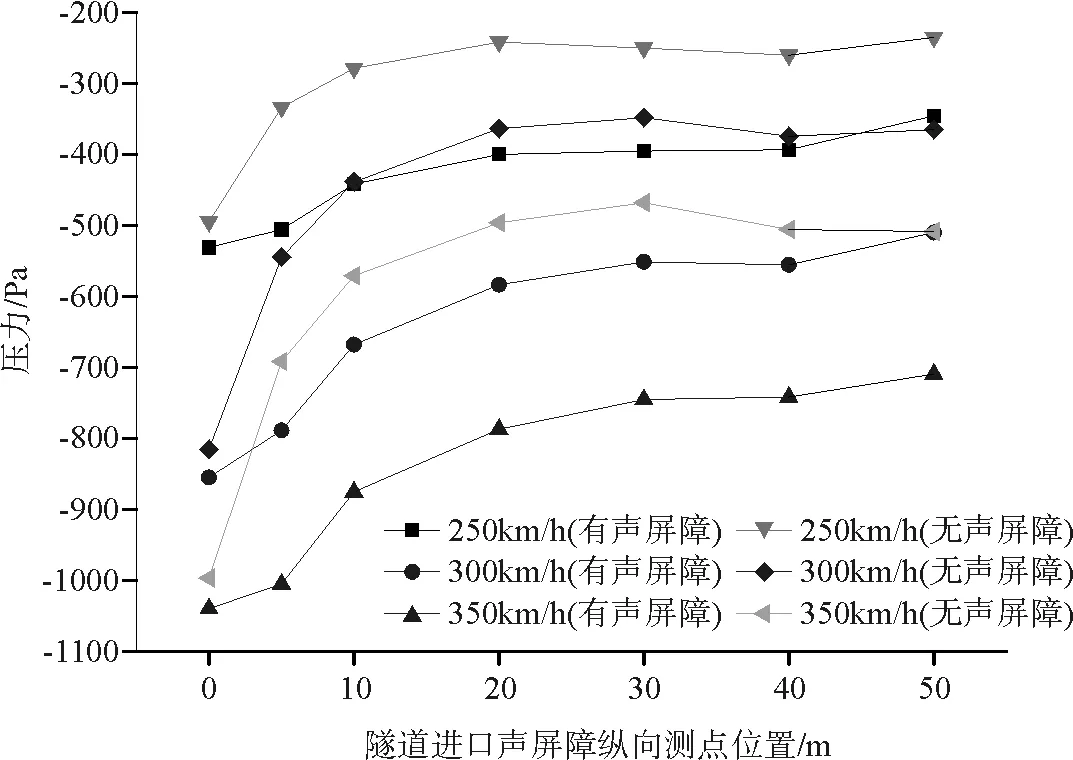
图15 隧道出口声屏障纵向测点头波波谷值压力变化

2.4 声屏障上受列车风压幅值与列车运行速度的关系

为探究声屏障上受到的列车风荷载幅值与列车运行速度之间的关系，取列车以不同速度通过设置在隧道口的声屏障区域时，声屏障面板竖向上中间位置(编号为c)的一纵行测点的计算结果进行分析[8]，其中列车运行速度分别取250 km/h、300 km/h、350 km/h、400 km/h，声屏障上受到的列车风压幅值与列车速度的关系曲线如图16、图17所示。

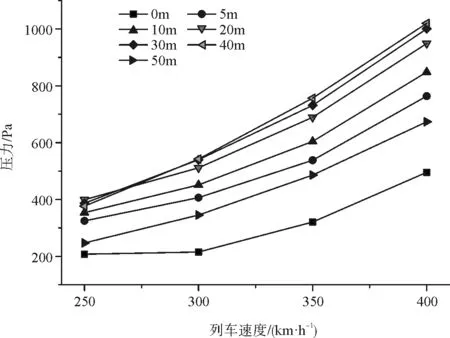
图16 隧道出口声屏障头波波峰幅值与车速的关系

图17 隧道进口声屏障头波波峰幅值与车速的关系

声屏障表面受到列车风荷载幅值与列车速度之间的关系曲线经过拟合处理后，可以获得它们之间的关系式:P=aV2+bV+c，其中P表示声屏障表面受到列车风荷载幅值，V表示列车速度(km/h)，a、b、c表示无量纲常数，与车速和测点位置有关。由此可知，列车单车通过隧道口声屏障区域时其表面受到列车风荷载幅值与列车速度成二次函数关系。

2.5 声屏障上受列车风压幅值与其距线路中心距之间的关系

为了探究声屏障上受列车风荷载幅值与其距线路中心线距离之间的关系，取列车以时速350 km/h通过设置在隧道口的声屏障区域时，声屏障距线路中心线的距离取3.25 m、4.25 m、5 m三种情况下声屏障面板竖向上取中间位置(编号为c)的一行测点结果进行分析，声屏障上受列车风荷载幅值与其距线路中心线距离之间的关系曲线如图18、图19所示。

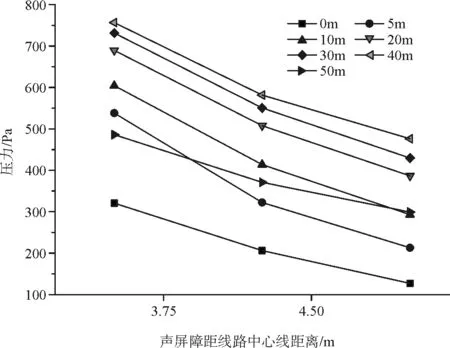
图18 隧道出口声屏障头波波峰幅值与其距线路中心距的关系

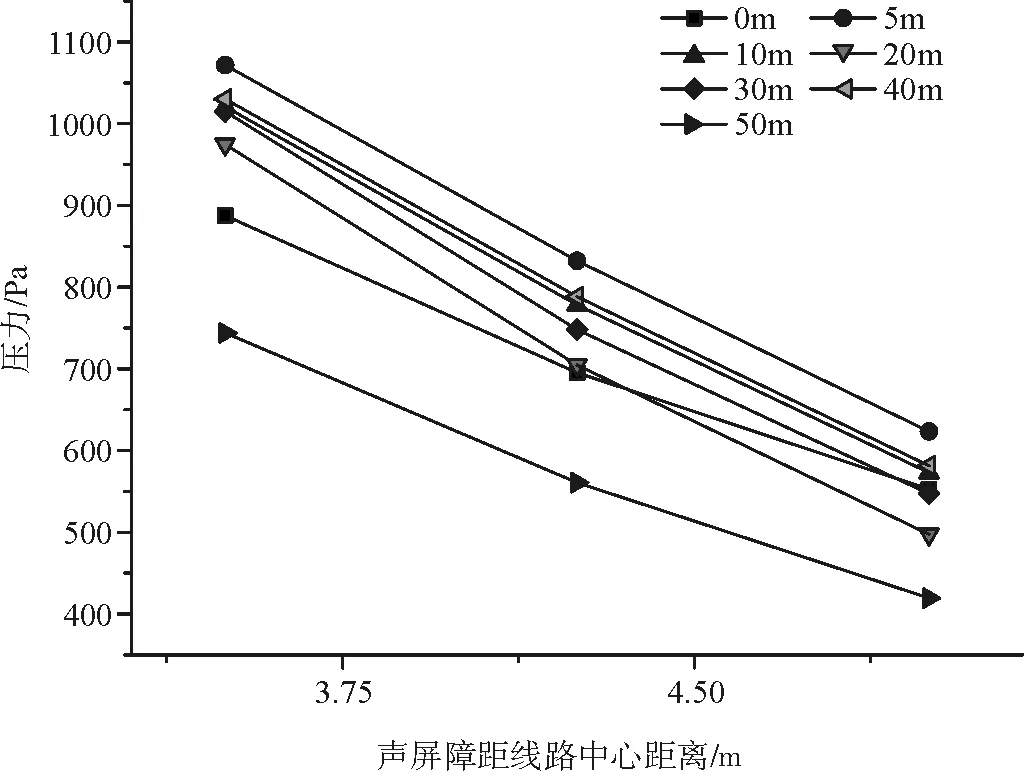
图19 隧道进口声屏障头波波峰幅值与其距线路中心距的关系

声屏障上受列车风荷载幅值与其距线路中心线距离之间的关系曲线经过拟合处理后，可以获得它们之间的关系式:P′=a′L2+b′L+c′，其中P′表示声屏障表面受到列车风荷载幅值，L表示声屏障距线路中心线距离(m)，a′、b′、c′表示无量纲常数，与声屏障距线路中心线距离和测点位置有关。由此可见，列车单车通过隧道口声屏障区域时其表面受到列车风荷载幅值与其距线路中心线的距离也成二次函数关系。同时，我们也可以发现,隧道口声屏障表面受到列车风 荷载幅值随其距线路中心线的距离的增加成递减变化。因此，我们得出在相同的吸声降噪的效果下，为保证声屏障的结构稳定和使用寿命，在环境允许的条件下，应该尽可能地增加声屏障距线路中心线的距离。

3 结论

本文通过对比分析隧道口声屏障上受到的列车风荷载与不同因素之间的关系，可以得到以下主要结论。

(1) 隧道长度对隧道口声屏障上受到的列车风荷载影响不大，基本可以忽略隧道长度的影响。

(2) 隧道口声屏障竖向高度上受到列车风荷载分布表现为：风压幅值从上至下增加，在其顶部区域变化率较大，底部区域幅值变化较小。

(3) 离隧道进口5 m范围内，声屏障受隧道口三维效应的影响较大；离隧道进口5～20 m范围内受三维效应影响相对小很多；离隧道进口20 m以外，声屏障就不再受到三维效应的影响。隧道进口三维效应的影响范围和列车运行速度关系不大，但影响强度随列车运行速度的增加而增加。越靠近隧道出口，声屏障受隧道出口三维效应的影响强度越大，列车速度越快，影响范围也就越大，隧道出口5 m范围内，声屏障上的脉动风压受影响强度要比隧道出口5 m范围外的大的多。在离隧道口相同位置处，设不设置声屏障对隧道口外三维效应的影响范围几乎没有影响。

(4) 列车单车通过隧道口声屏障区域时声屏障表面受到

列车风荷载幅值与列车速度和其距线路中心线的距离都成二次函数关系。

[1] Deng Yongquan, Xiao Xinbiao, He Bin,etal. Analysis of external noise spectrum of high-speed railway[J]. J.Cent.South Univ, 2014, 21(12): 4753-4761.

[2] G·Kouroussis, N·Pauwels, P·Brux,etal. A Numerical Analysis of the Influence of Tram Characteristics and Rail Profile on Railway Traffic Ground-Borne Noise and Vibration in the Brussels Region[J]. Science of the Total Environment, 2014, 483(13): 452-460.

[3] 廖欣，王东镇，孙召进，等. 高速列车进出隧道噪声问题及控制[J]. 声学技术，2010，29(4)：324-327.

[4] 叶葵葵，张克跃，张继业，等. 高速铁路隧道外声屏障气动荷载的数值模拟研究[J]. 四川建筑，2016，36(3)：156-160.

[5] 叶葵葵. 高速列车通过隧道口声屏障气动性能及动力特性分[D]. 西南交通大学, 2016.

[6] 龙丽平，赵丽滨，刘立东. 列车致声屏障结构的空气脉动力研究[J]. 工程力学，2010，27(3)：246-250.

[7] 张亮，张继业，张卫华. 高速列车通过声屏障的流固耦合振动响应分析[J]. 动力学与控制学报，2014，12(2)：153-159.

[8] 李红梅，宣言，王澜，等. 高速铁路声屏障脉动力数值模拟研究[J]. 铁道建筑，2013，52(1)：27-30.