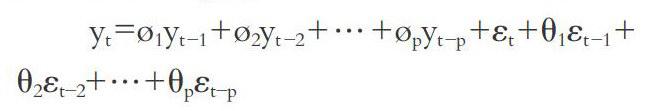基于ARMA模型的CPI短期预测研究
2018-05-08袁志强陈锐
袁志强 陈锐
摘要:文章利用2012年1月到2017年8月月度全国居民消费价格指数,探索运用R软件forecast n程序包中的auto,anma()函数进行最优ARIMA模型构建、模型检验、及短期预测。研究主要得出两点结论,1.构建了ARIMA(1,1,0)模型,检验结果合理。2.预测出2017年8月以后连续6个月的月度CPI,分别为101.6549、101.7975、101.6884、101.6954、101.6928、101.6938。
关键词:AKMA模型:CPI;R语言
一、引言及文献综述
一直以来,通货膨胀都是世界各国经济发展过程中必须重视的重大问题,其预测也是各国所面临的一项重大课题。我国经过近40年的高速发展,通货膨胀问题开始不断引起人们的重视,通过膨胀的预测已然成为一项紧迫的课题。对作为衡量通货膨胀重要指标的居民消费价格指数(CPI)进行预测,就显得十分必要。
近10年来,ARMA模型了受到学者们的广泛青睐。主要因为其具有较强的扩展性和现实性。既可以拟合AK、MA、ARMA、SAKIMA等模型,又更加符合经济政策存在时滞的现实,国外有代表性的如Alnaa和Ahiakpor(2011)以加纳为研究对象,运用Box-lenkins建模方法建立ARIMA(6,1,6)模型,对月度通货膨胀率进行预测,结果显示ARIMA模型在通货膨胀预测中具有较好的效果。国内有代表性的近期的如,肖良(2016)以居民消费价格指数(cPI)的短期预测为切入点,运用定量的时间序列分析方法,建立季节性ARI-MA模型对CPI时间序列进行量化分析,在实证分析中探讨经济变量CPI与时间变量之间的变动规律,对CPI时间序列进行适当的差分,取得了较为理想的预测效果。孙舞渊,伍海军(2017)基于考虑春节效应的X-12-APJMA季节调整模型,对我国2002年1月至2013年12月的CPI序列月度数据进行季节调整,并进行季节波动性分析和短期预测。研究结果表明:我国的CPI变动存在明显季节性特征,春节效应对其有显著影响;CPI序列的短期波动主要是受季节性成分影响,而长期波动主要受趋势——循环成分影响:利用该模型进行短期预测的效果较好,预测误差绝对值控制在1.5%之内。虽然国内外关于ARMA模型的应用已经有了大量研究,但在进行CPI预测方面还没有形成一个统一、公认、可靠的模型,对于CPI短期预测的ARMA模型的短期预测还有待进一步探索。另外,到目前为止,在进行AKMA模型构建的过程中,研究者基本都是运用EViews软件进行操作,而对于现在开始不断流行的R软件,还有待不断实践和推广。本文将探索运用R语言基于ARMA模型对2017年8月后连续6个月的CPI进行短期预测。
二、ARMA模型介绍
(一)ARMA模型简介
AKMA模型,即自回归移动平均模型,由Box和Ienkins于1994年提出,其基本思想是把AK模型和MA模型结合在一个紧凑的形式中,来描述经济变量的变化趋势,并据此对未来的变化作出预测。ARMA(p,q)模型的基本形式为:
式中,p为自回归部分的滞后阶,q为移动平均部分的滞后阶,εt为随机误差项,通常要求为白噪声过程。有时也称时间序列{yt}服从ARaMA(p,q)过程,记为:ycARMA(p,q)。ARMA模型包含两个特例形式,当q=0时,ARMA(p,q)模型退化为自回归AK(p)过程;当p=0时,ARMA(p,q)模型便退化为移动平均MA(q)模型。
(二)ARMA模型的建模过程
1.序列识别。首先,判断建模分析的数据是否为平稳序列,若为非平稳序列需对其进行变换处理,使其变为平稳序列。接着再判断平稳的序列是否为白噪声序列,若为白噪声序列则列建模结束(白噪声过程无法构建ARMA模型):若为非白噪声序列,则进行下一步。
2.模型识别与估计。决定p和q的值,选出相对最优的模型结构。此处直接使用R软件中的auto,arima()函数进行最优模型定阶。
3.模型诊断。对模型残差进行检验,确保其为服从正态分布的白噪声序列。当模型的残差是白噪声时说明已经将序列的信息充分提取到模型中,
三、数据来源及整理
本研究数据为我国2012年1月至2017年8月连续月度CPI,共68组,取自东方财富网,网址http://data.eastmoney.com/cjsj/consumerpriceindex.Aspx?P=1。数据整理见表1。本文将探索运用R语言对CPI进行建模和预测,这也是本文的一个亮点。利用代码data=read.table(“clip-board”,header=T),将CPI数据导入RStudio。
四、模型的构建
(一)平稳性检验
时间序列的平稳性是AKMA模型建模的基础,所以,在模型构建之前我们要先对CPI数据进行平稳性检验。运用R软件作ADF检验,检验结果如下:
Augmented Dickey-Fuller Tesc
data:CPI
Dickey-Fuller=-3.4063,Lag order=4,
p-value=0.06225
alternative hypothesis:stationary
從检验结果可以看到,p值为0.06225,表示在10%的显著性水平下拒绝原假设,CPI时间序列平稳。
(二)模型构建
首先加载forecast程序包,然后根据mod=auto,arima(CPI)进行最优模型建模。建模结果如下:
Series:CPI
ARIMA(1,1,0)
Coefficients:
at1
-0.3628
s.e.0.1212
sigma^2 estimated as 0,1991:log likeli-
hood=-40.55
AIC=85.09
AICc=85.28
BIC=89.5
从输出结果可以看出,auto,arima函数自动拟合的最优模型是ARIMA(1,1,0)模型。一阶自回归系数为-0.3628,残差为0.1212,σ2估计为0.1991,似然估计对数值为-40.55,赤池信息量AIC值为85.09,AICc值为85.28,贝叶斯信息量BIC值为89.5,
(三)模型诊断
1.系数显著性检验。根据contint()函数对上述模型mod进行系数显著性检验,检验结果如下:
2.5%
97.5
ar1-0.6003447-0.1252672
检验结果显示,-0.6003447、-0.1252672之间不包含0。表示:在5%显著性水平下,一阶自回归系数显著,ARIMA(1,1,0)模型通过系数显著性检验。
2.白噪声检验。根据Box检验,Box,test(res,lag=10,type=c(”Ljung-Box",))得出检验结果如下:
Box-Ljung test
data:res-
X-squared=6.479,df=10,p-value=0.7735
从检验结果可以看出,p值为0.7735,接受原假设,残差是服从正态分布的白噪声序列。模型再次通过白噪声检验。
五、预测及分析
根据predict()函数对2017年8月以后连续6个月的CPI进行预测,结果如下:
$pred
Time Series:
Start=69
End=74
Frequency=1
[1]101.6549 101.7075 101.6884 101.6954101.6928 101.6938
从预测结果表2可以看出,预测出的6个月CPI值没有出现异常值,且同2017年1至8月CPI值相差不大。表明预测结果较为合理。另外,从连续6个月的预测值还可以看出,在接下来的6个月中,我国居民消费价格在时间上虽表现出一定波动,但总体表现平稳。
六、结语
本文的研究主要集中于2012年及之后的居民消费价格指数问题,通过实证分析,主要得出以下两点结论。
1.模型拟合良好。系数显著性检验结果显示,在5%显著性水平下,一阶自回归系数显著,ARIMA(1,1,0)模型通过系数显著性检验。残差检验结果显示,p值为0.7735,接受原假设,残差是服从正态分布的白噪声序列,模型再次通过白噪声检验。表明模型拟合良好。
2.未来6个月我国居民消费价格总体表现平稳。本文通过ARIMA(1,1,0)模型運用predict()函数对2017年8月以后连续6个月的CPI进行了短期预测,预测结果分别为101.6549、101.7075、101.6884、101.6954、101.6928、101.6938。预测结果显示我国居民消费价格在时间上虽表现出一定波动,但总体表现平稳。