抽水蓄能机组调速系统实测建模与仿真研究

韩文杰

（清远蓄能发电有限公司，广东清远511853）

0 引言

南方电网具有远距离、大容量输电、交直流混合运行、系统调峰调频能力低、电源形式多样、线路架构复杂等特点。大型抽水蓄能机组调速器系统的动态特性不仅影响机组自身的安全性和经济性，而且对整个电网会产生一定的影响。因此，获取准确可靠的原动机及调速系统模型参数，进行相关仿真计算，了解其动态特性及对负荷变动的适应能力，探讨其动态特性对电网的影响是非常必要的。本文以清远抽水蓄能电站（简称清蓄）2号蓄能机组为例，介绍抽水蓄能机组原动机及调速系统实测建模与仿真的研究。

1 调速系统组成及主要技术参数

清蓄2号机组原动机及调速系统由AGC系统、电子调节器、执行机构、引水和泄水系统、水轮发电机组和测量元件构成，如图1所示。电子调节器和执行机构构成水轮机调速器，电子调节器接收机组频率、功率和AGC系统的负荷给定信号并在内部实现频率和功率闭环调节，执行机构按一定特性将电子调节器的输出转换成主接力器行程偏差，从而控制机组功率、转速。

清蓄2号机组电子调节器为法国ALSTOM研制的TSLG型功能组合式数字调节器，为UPC+SPC的双通道冗余结构，与计算机监控系统相配合，完成水轮发电机组的开机、停机、增减负荷、紧急停机等任务，其主要性能参数见表1。

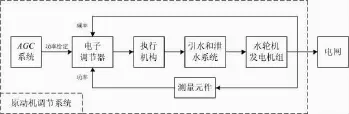
图1 原动机调速系统框图

表1 清蓄2号机组电子调节器参数表

抽水蓄能机组有水轮机和水泵两种工况，做水泵工况运行时，调速器根据水头控制导叶的开度，不参与电网调节。建立抽水蓄能机组仿真模型只是针对参与电网调节的水轮机工况。

2 调速系统模型及仿真

水轮机及其调节系统模型由3个部分组成：电子调节器模型、执行机构模型和原动机模型。调节系统模型输出YPID信号，执行机构模型根据YPID信号模拟导叶开度的动作情况，以此影响原动机模型的仿真功率输出，各模型具体结构如下。

2.1 电子调节器部分（GMGM+）

根据厂家提供的电子调节器资料。采用PSD-BPA（4.15版）暂态稳定程序中的GMGM+卡搭建电子调节器模型仿真系统如图2所示。其中，fg为机组频率（标么值），fc为频率给定（标么值），DELT为频率测量的延迟时间（s），DELT2为功率或开度测量的延迟时间（s），TR1为频率测量环节时间常数（s），TR2为功率或开度测量环节时间常数（s），bp为功率或开度调差系数，DB1为转速死区（标么值），DB2为功率或开度死区（标么值），DB1MAX为一次调频上限，DB1MIN为一次调频下限，DB2MAX为功率或开度上限，DB2MIN为功率或开度下限，KP为比例增益，KI为积分增益，KD为微分增益，T1v为微分时间常数（s），INT1max为积分上限，INT1min为积分下限，YPIDmax为调节器输出上限，YPIDmin为调节器输出下限，ITYP为模式选择开关（=1为功率模式，=2为开度模式），ITYP2为开度模式选择开关（此开关在ITYP=2时有效，=0输入信号为开度Y，=1输入信号为Ypid），YPID为电子调节器输出。

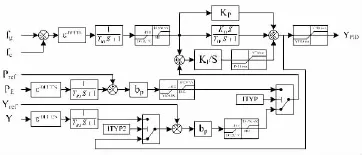
图2 电子调节器计算模型

模型参数依据清蓄电站2号机组调速系统设备资料进行设置，调速器频率给定50Hz，阶跃量为-0.15Hz，调速器自动控制，开度模式，调节参数Intd_bp＝4%、Intd_Kp＝5、Intd_Ti＝2.8s、Intd_Td＝0s、Sn_Kd=5、ef=0.05Hz。仿真利用图2所示计算模型进行，其参数设置为：fg为实测频率，fc=1，DELT=0s，TR1=0.001 s，DELT2=0 s，TR2=0.001 s，bp=0.040，DB1=0.001，DB1MAX=inf，DB1MIN=-inf，DB2=0，DB2MAX=inf，DB2MIN=-inf，KP=5，KI=1.7s-1，KD=0s，T1v=0.01，INT1max=inf，INT1min=-inf，ITYP=2，ITYP2=1。为方便仿真计算的进行，忽略空载开限与最大开限，将 YPID输出限幅设置为YPIDmax=1，YPIDmin=0。

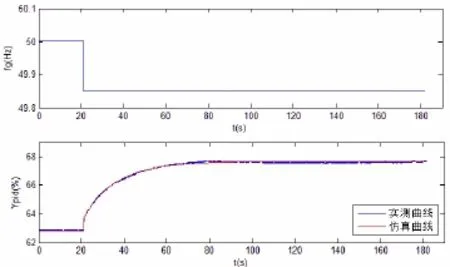
图3 实测与仿真的调速器输出曲线对比

由图3可知，YPID的实测曲线和仿真曲线基本吻合，说明电子调节器部分的模型正确、合理。

2.2 导叶执行机构部分（GAGA+卡）

根据厂家提供的导叶执行机构资料。采用PSD-BPA（4.15版）暂态稳定程序中的GMGM+卡搭建导叶执行机构仿真系统如图4所示。其中，YPID为电子调节器输出，Y为导叶执行机构输出（接力器行程），Kp为比例增益，Ki为积分增益，Kd为微分增益，INT2max为积分上限，INT2min为积分下限，PIDmax为PID环节输出上限，PIDmin为PID环节输出下限，VELopen为开启速度限幅，VELclose为关闭速度限幅，Ty为导叶主接反应时间常数，Ymax为导叶主接最大行程，Ymin为导叶主接最小行程，T1为接力器行程测量环节时间常数（s），Ydelay为导叶执行机构输出的延迟时间（s）。

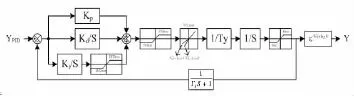
图4 导叶执行机构计算模型

通过内部程序直接给定PID指令的方法实测导叶开度变化。导叶最快开启、关闭实测曲线与仿真的对比如图5所示。仿真数据由图4所示模型仿真计算获得，其中参数为：Kp=1.6，Ki=0，Kd=0，INT2max=inf，INT2min=-inf，PIDmax=inf，PIDmin=-inf，VELopen=0.0175， VELclose1=-0.145， VELclose2=-0.011，Ty=1.371，Ymax=1，Ymin=0，T1=0.001s，Ydelay=0s。

图5 导叶最快开启关闭实测与仿真曲线对比

由图5可知，Y的最快开启、关闭实测曲线和仿真曲线趋势一致，说明执行机构开启、关闭方向的速度限幅整定是正确的。

静态模拟一次调频动作时执行机构输出实测与仿真的对比如图6所示。实测数据和电子调节器输出实测与仿真的对比采用的一致。仿真数据亦由图4所示模型仿真计算获得，参数和前面一致。

由图6可知，Y的实测曲线和仿真曲线趋势一致，基本吻合，说明执行机构部分模型正确、合理。

图6 模拟一次调频动作时执行机构输出实测与仿真曲线对比

2.3 原动机部分（TW卡）

原动机部分给出两种仿真模型，①为PSD-BPA暂态稳定程序中使用的考虑刚性水击的理想水轮机模型（TW卡）；②考虑某一水头下出力与导叶开度对应关系的改进型刚性水击模型。

1）BPA模型（TW卡）

PSD-BPA暂态稳定程序中使用的考虑刚性水击的理想水轮机模型如图7所示。

图中，Y为接力器行程，P为原动机输出（有功功率），Tw为水流惯性时间常数。

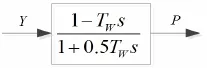
图7 BPA中的原动机计算模型（TW卡）

模拟一次调频动作时，原动机输出实测曲线与BPA中原动机模型（TW卡）仿真结果的对比如图8。试验条件为：调速器频率给定50Hz，调速器自动控制，负载功率模式，调节参数为Intd_bp=4%，Intd_Kp=5，Intd_Ti=2.8，Intd_Td=0，ef=0.05Hz，初始功率大约211MW，一次调频投入，机频阶跃扰动-0.15Hz。设置图7所示模型中的Tw等于1.14s。

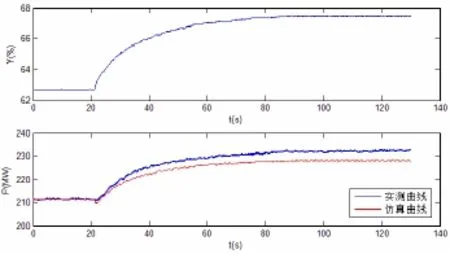
图8 模拟一次调频动作时原动机输出实测与仿真曲线对比

2）改进的刚性水击模型

图7所示模型其等价控制框图如图9所示。

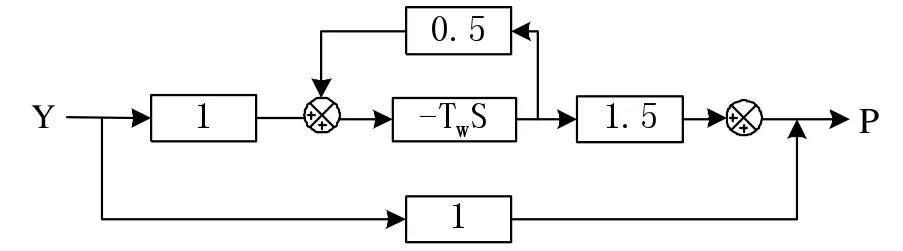
图9 考虑刚性水击的理想水轮机模型（TW卡）框图

忽略系统变化影响的简化的混流式水轮机机组段框图如图10所示。

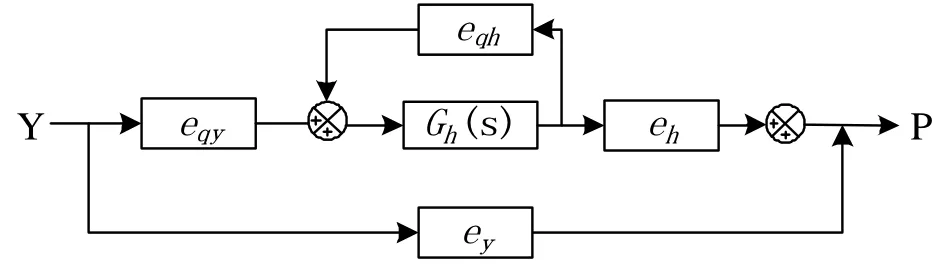
图10 简化的混流式水轮机机组段框图

由对比可知，TW卡所代表的水轮机模型是将图 10 中参数设为：eqy=1，ey=1，eh=1.5，Gh(S)=-TWS。其中，ey=1表示机组出力正比于导叶开度变化，机组空载和满负荷分别对应导叶的全关和全开。而实际上抽水蓄能机组水头变化较明显，当实际工况点偏离额定工况点较远时，机械功率与导叶开度存在较为明显的非线性关系，考虑某一水头下水轮机功率与开度的非线性特性，原动机部分的计算模型采用改进的刚性水击模型，如图11所示。

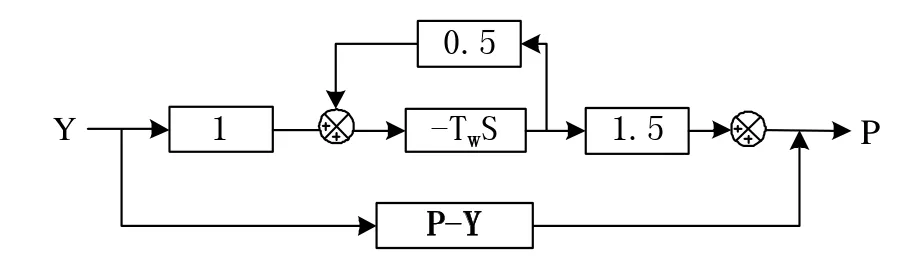
图11 改进的刚性水击模型

通过对比图11和图9可知，改进的刚性水击模型是通过实测机组某一水头下出力与导叶开度对应值，获得对应关系拟合方程，代替TW卡中取值为1的ey，构成改进型原动机模型。

通过实测试验可知清蓄2号机组在上库水位600.39m，下库水位129.69m时导叶开度与有功功率对应关系见表2。

导叶开度与有功功率拟合关系式见式（1）。

实测开度-功率关系曲线对比图如图12所示。

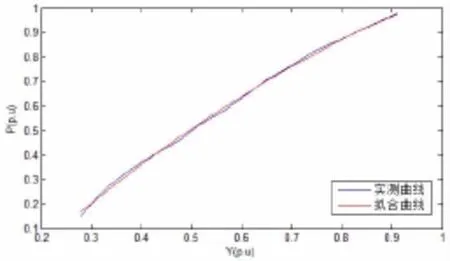
图12 开度与功率对比曲线

模拟一次调频动作时，原动机输出实测曲线与改进的刚性水击模型仿真结果的对比如图13所示。试验条件为：调速器频率给定50Hz，调速器自动控制，负载功率模式，调节参数为Intd_bp=4%，Intd_Kp=5，Intd_Ti=2.8，Intd_Td=0，ef=0.05Hz，初始功率大约211MW，一次调频投入，机频阶跃扰动-0.15Hz。图11所示改进刚性水击模型的参数设置为：P—Y关系曲线为式(1)，Tw=1.14s。

图13 模拟一次调频动作时原动机输出实测与仿真曲线对比

对比图8和图13可知，输入的导叶接力器行程一致的情况下，改进的刚性水击模型的仿真功率输出曲线与PSD-BPA暂态稳定程序中的TW卡采用的原动机模型的仿真功率输出曲线相比，前者更加接近实测结果。

2.4 调速系统模型及参数

（1）原动机采用改进的刚性水击模型的调速器系统

调速系统的计算模型如图14所示。

图14 采用改进的刚性水击模型的调节系统模型

将动态下频率扰动试验的频率信号作为图14中的fg，即可对动态模拟一次调频动作时的调速系统工作情况进行仿真。模型参数依据清蓄2号机调速系统设备资料进行设置，其中调速器频率给定50 Hz，调速器自动控制，负载功率模式，调节参数为Intd_bp=4%，Intd_kp=5，Intd_Ti=2.8，Intd_Td=0，Sn_Kd=5、ef=0.05Hz，初始功率大约 210MW，一次调频投入。实际输出与仿真曲线的对比见下页图15。

由图15可知，电子调节器Ypid输出值、导叶接力器行程、有功功率的实测曲线与仿真曲线趋势一致，调节过程基本吻合，最终稳定值基本一致。仿真结果与实测结果偏差对比见表3，符合《导则》要求。

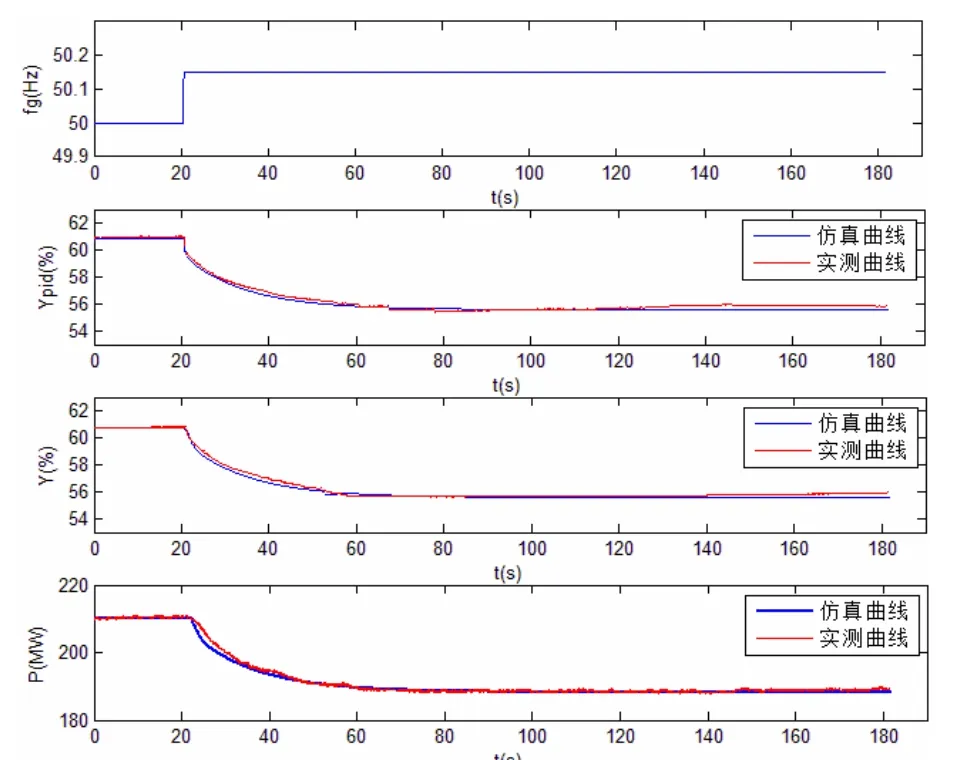
图15 动态下频率阶跃0.15Hz时调速系统各部分实测输出与仿真曲线对比

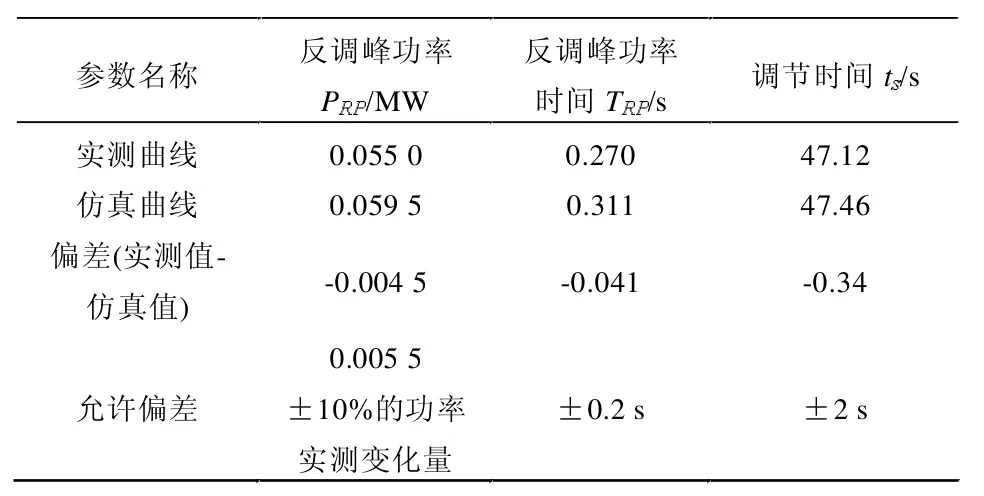
表3 动态下频率阶跃0.15Hz时仿真与实测偏差对比

（2）原动机采用BPA模型（TW卡）的调速器系统

将原动机模型更换为图9所示的TW卡模型再次进行仿真计算，参数设置与图14相同各部分实际输出与仿真曲线的对比见图16。

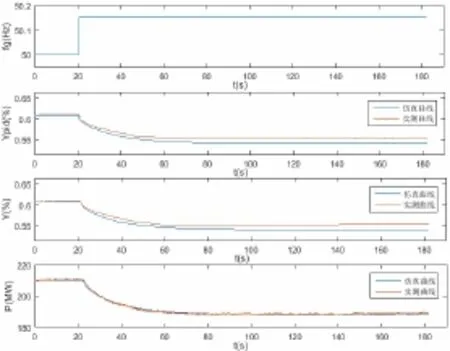
图16 动态下频率阶跃0.15Hz时调速系统各部分实测输出与仿真曲线对比

由图16可知，有功功率的实测曲线与仿真曲线趋势基本一致仿真结果与实测结果偏差对比见表4，符合《导则》要求。

与采用改进的刚性水击模型的仿真结果相比，电子调节器与执行机构的输出在调节过程和最终稳定值上与实测数据存在一定误差。

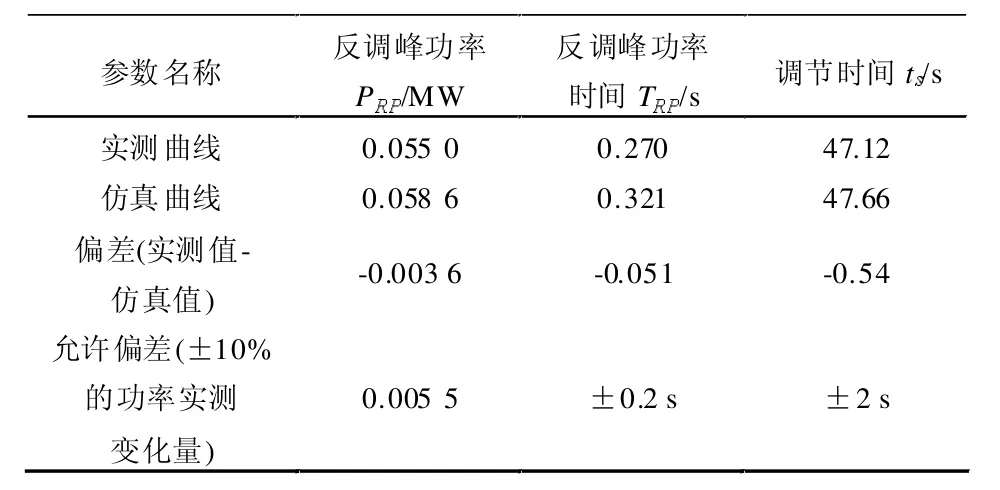
表4 动态下频率阶跃0.15Hz时仿真与实测偏差对比

实际机组与仿真模型均采用功率闭环调节，在调节参数设置合理的情况下，实测与仿真功率的调节过程与最终稳定值是一致的。由于原动机部分采用不同的模型，表达功率与开度关系的传递函数不同，导致相同功率所对应的开度值不同，从而使电子调节器与执行机构输出的实测与仿真值存在误差。

3 结论和建议

（1）对比BPA模型（TW卡），相同导叶开度变化下，改进的刚性水击模型仿真的功率响应过程更贴近实际；相同功率闭环阶跃扰动下，改进的刚性水击模型仿真的电子调节器与执行机构的输出亦更接近实际。

（2）BPA暂态稳定程序中提供的水轮机调速器和原动机模型（TW卡）的传递函数直接将功率与开度关系线性化，导致开度的响应曲线与实测曲线在部分时段存在差别。随着电力系统对仿真计算精度要求的提高以及电力系统控制逐步趋于复杂化，BPA模型（TW卡）已经很难准确仿真目前新型微机调速器的工作情况，建议在BPA暂态稳定程序中完善模型结构、改进建模方法，从而为电力系统仿真研究提供与实际系统状况相吻合的调节系统模型，满足电力系统稳定计算的要求。

参考文献：

[1] 李悝，张靖，孙海顺，等.水轮机及其调速系统建模与参数辨识方法[J].水电能源科学，2006，24（4）：79-81.

[2] 巩宇.抽水蓄能机组原动机及调节系统参数实测与建模研究[J].水电站机电技术，2011，34（4）：9-14.

[3] 张承慧，刘玉庆.水轮机建模与参数识别[J].电力系统自动化，1997，21（5）：53-56.

[4] 彭天波，杨洪涛.抽水蓄能机组原动机及调速系统参数实测、建模与仿真[C]//第18次中国水电设备学术讨论会论文集，2011.