起伏地形下可控源音频大地电磁三维数值模拟

钟苏美，林昌洪，谢裕春

(1.上海勘测设计研究院有限公司，上海 200434； 2.中国地质大学(北京) 地球物理与信息技术学院，北京 100083；3.北京城建勘测设计研究院有限责任公司，北京 100101)

0 引 言

加拿大学者Goldstein和Strangway[1]在20世纪70年代提出可控源音频大地电磁法(CSAMT)。近40多年来，CSAMT得到了快速的发展，目前已广泛地应用于矿产、油气和地热等资源探测以及水文环境和地质工程等领域[2-17]。然而，大多数的CSAMT工作是在存在地形起伏的区域开展的，很少在水平地表条件下采集CSAMT数据。前人研究已表明：地形对CSAMT数据存在强烈的影响，因此在CSAMT数据反演处理解释时需要考虑地形。

近年来，随着计算机技术的进步，CSAMT二维正反演算法的研究逐渐趋于成熟，并且很多二维正反演算法也开始考虑地形的影响。例如，Mitsuhata[3]采用有限单元法实现了考虑地形的CSAMT二维正演。李予国等[2]采用有限单元法实现了考虑海底地形起伏的海洋可控源电磁法(CSEM)的二维数值模拟。雷达等[13]采用有限元法实现了起伏地形下CSAMT二维正反演研究。然而，使用二维正反演方法的前提是假设地下电阻率结构是二维分布的，并且测线与二维电阻率结构走向垂直。但是，实际地下地质情况和地表的地形情况通常比较复杂，地质结构和地形大部分情况下都是三维的。前人对水平地表的大地电磁数据的研究表明，采用二维反演技术处理三维异常体产生的数据，很可能得到不可靠的地电模型，有时甚至得到畸变的结果。采用二维地形处理技术去逼近三维地形，也会导致类似的错误解释结果。因而，需要有考虑三维地形起伏条件的三维CSAMT正、反演算法用于CSAMT数据的处理与解释，以此能够得到更加可靠的数据解释结果。

开展带地形三维CSAMT反演研究的前提是：先研究带地形三维CSAMT正演模拟算法。Zhdanov等[5]2006年采用积分方程方法实现了考虑地形的三维海洋CSEM数值模拟。Sasaki[6]2011年采用有限差分法实现了考虑地形的三维海洋CSEM数值模拟。Schwarzbach等[10]2011年采用有限单元法实现了考虑地形的三维海洋CSEM数值模拟。然而，CSEM数值模拟中关于海底地形处理，与CSAMT数值模拟中关于地表地形的处理存在一些差别：海底地形分界面两侧的海水(其电阻率约为0.3 Ω·m)与海底介质(约1 Ω·m)的电阻率差异不明显，而地表地形分界面两侧的空气(无穷大)与地下介质(小于105Ω·m)的电阻率差异非常大。因此，CSAMT数值模拟中处理地形，需要更加谨慎。前人关于水平地表CSAMT三维数值模拟的研究较多[11-17],但目前还没有考虑三维地表地形的CSAMT三维数值模拟报道。

本文介绍一种采用有限差分法模拟三维起伏地形的三维CSAMT响应算法。与Sasaki[6]采用的有限差分法模拟海底地形的三维海洋CSEM响应算法不同的是：(1)本文模拟三维地表地形；(2)本文采用不同的方式处理场源奇异性。由于场源附近的电场和磁场变化非常迅速，如何处理场源奇异性的策略通常有两种：(1)采取将电磁场总场分离成背景场和二次场的策略；(2)采用伪δ函数来代替场源直接计算总场的策略。正如Mitsuhata[3]在考虑地形的CSAMT二维数值模拟的研究中所述：当地下介质复杂的情况下，很难找到一个简单的背景场构造，而采用伪δ函数来代替场源直接计算总场的策略不存在这个问题，因此更适合于模拟复杂地质结构。本文中，首先将简单介绍采用有限差分法如何模拟考虑地形的三维CSAMT响应， 然后给出理论模型的模拟结果，最后对三维数值模拟算法的正确性进行检验。

1 有限差分法模拟起伏地形的三维CSAMT响应

本算法是在林昌洪等[11]提出的有限差分法求解水平地表条件下三维CSAMT 响应算法的基础上修改代码实现的，因此下面将简单介绍有限差分算法，重点介绍与水平地表三维CSAMT 数值模拟算法[11]的不同之处。

1.1 电磁场耦合方程

可控源音频大地电磁法工作频率范围为0.1～10 000 Hz，在此频段可忽略位移电流的作用，地下介质和空气的磁导率相接近。在电偶极子或者水平线圈激发情况下,总电场强度矢量E和总磁场强度矢量H相互作用的关系满足麦克斯韦方程：

∮Hdl=∬(σE+Js)ds

(1)

∮Edl=∬iωμ0Hds

(2)

式中：ω表示角频率；μ0为真空磁导率；σ为介质的电导率；E表示电场强度；H表示磁场强度；Js为源电流密度。

1.2 场源奇异性处理

在水平地表三维CSAMT 数值模拟算法[11]中，也是采用将总场分离成背景场和二次场，最后合成总场的策略处理场源奇异性。由于直接模拟总场的策略更适合于模拟复杂地质结构，参考Mitsuhata[3]提出的CSAMT二维数值模拟的策略，在本文的考虑地形三维CSAMT数值模拟中，使用伪δ函数代替场源直接模拟总场以解决场源的奇异性，伪δ函数表达式如下：

δs(x-x0)=

(3)

其中：x0是源的横坐标；τ是常数，控制等效场源作用的范围和幅值。

当源和研究区域都是三维时，伪δ函数的表达式为:

δ(z-z0)

(4)

式中：r0为场源的矢量坐标；x0、y0、z0分别表示场源X轴坐标、Y轴坐标和Z轴坐标。

根据伪δ函数的表达式，式(1)中的源电流密度Js可写成：

(5)

式中：I为场源电流强度；L为场源长度。

1.3 三维正演方程

在笛卡儿右手坐标系中，用交错采样剖分网格[18]在研究区域内对电阻率和电磁场总场满足的麦克斯韦积分方程(1)和(2)进行离散化，可获得关于地下各网格单元采样点处总磁场的正演方程：

AU=b

(6)

其中：A为n×n阶对称大型稀疏系数矩阵；U为待求解总磁场分量构成的n×1维列向量；b为一个与边界场值和场源有关的n×1维列向量；n为待求解的未知磁场分量的个数。采用预条件的双共轭梯度稳定算法[18]，求解该线性方程组，从而获得总磁场值列向量。

1.4 边界条件

在水平地表三维CSAMT 数值模拟算法[10]中，由于求解的是二次磁场，采取研究区域的空中顶边界、地下底边界和4个侧边界处的二次磁场值为零的方法处理边界条件。当选择合适的背景电阻率求解一次场时，二次场基本由异常体的剩余电阻率(电阻率-背景电阻率)产生，而且研究区域的空中顶边界、地下底边界和4个侧边界处离异常体较远，因此求解二次磁场时可以采用边界二次磁场值为零的边界条件。但是，在本文中是直接计算总场，总场在上述边界处的磁场值不满足为零的条件，因此，不能采用相同的策略。

本文中，笔者仍然采用第一类边界条件。在有限差分数值模拟中，常常把区域剖分得足够大，让异常体和场源距离边界足够远，边界上的总电磁场基本满足远区条件。因此，可以认为在边界上的总磁场是均匀半空间中电偶极子在远区产生的一次磁场响应。参考Ward和Hohmann[9]的分析，地表水平电偶极子在均匀半空间中产生一次磁场表达式，加上准静态和远区场条件，可以将原一次磁场表达式进一步简化，得到X方向电偶极子在地表、接收在空中的远区一次磁场响应的计算表达式如下：

(7)

(8)

(9)

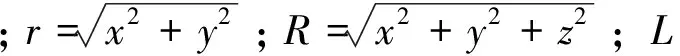
X方向电偶极子在地表、接收在地下的远区一次磁场响应的计算表达式如下：

(10)

(11)

(12)

Y方向电偶极子在地表、接收在空中的远区一次磁场响应的计算表达式如下：

(13)

(14)

(15)

Y方向电偶极子在地表、接收在地下的远区一次磁场响应的计算表达式如下：

(16)

(17)

(18)

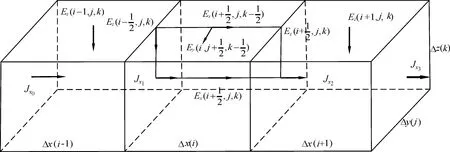
图1 地表处用于计算地表总电场的差分关系Fig.1 View of the difference relationship used to calculate the total electric fields on the surface

1.5 地形处理

求解方程(6)可得到地下交错采样点上的总磁场值U。得到总磁场值U后，需要计算地表(水平或是起伏地形)处的总电场和总磁场值，进而利用林昌洪等[11]提出的地表总电场和总磁场计算表视电阻率和相位的表达式计算得到地表处的视电阻率和相位响应。

不考虑磁导率参数，磁场在空气-地下介质分界面处的法向磁场和切向磁场都是连续的，因此，无论水平地表的磁场还是起伏地形分界面处的磁场，其求解表达式是一样的。可以利用采样点处的总磁场值，通过和水平地表同样的线性插值公式计算得到地表网格顶面中心处的总磁场的三个分量。

对于水平地表的电场，通过麦克斯韦方程▽×E=-iμ0ωH，地表网格顶面中心处的总电场的x分量(图1)可以通过下列表达式计算：

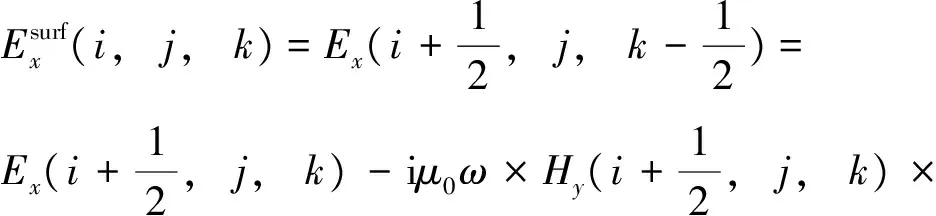
(19)

ρ(i,j,k)

(20)

(21)

但是，对于起伏地形分界面处总电场的x分量不能采用上述公式计算。例如，网格块 (i,j,k)在地下，而(i-1,j,k)在空气中时，靠近分界面处的法向电流密度变化梯度大，公式(20)采用界面处法向电流密度进行插值，计算结果不够精确。为了得到更为精确的结果，可以采用分界面右侧2个网格处的电流密度(图1)进行线性插值，从而公式(20)变为：

Jx2-Js]×ρ(i,j,k)

(22)

如Wannamaker等[4]所述，为了避免和空气-地下分界面有关的场值偏导数的不连续性，应该选择计算偏导数的2个场值的节点都位于同一介质中。网格块 (i,j,k)在地下而(i-1,j,k)在空气中时，计算公式(21)时也应采用位于同一介质内2个节点的垂直电场进行计算场值的偏导数，避免计算结果的不精确。

当网格块 (i,j,k)在地下，而(i+1,j,k)在空气中时，公式(20)和(21)可以做类似的修改。对于网格块 (i,j,k)在地下，而(i+1,j,k)和(i-1,j,k)都在空气中的情况，在网格剖分的时候应避免类似的剖分。

2 算法验证

为了检验算法的有效性和正确性，笔者设计一个水平地表下的三维异常体模型，将本文算法的计算结果和水平地表CSAMT三维正演算法[11]的计算结果进行对比。同时为了检验本文开发的带地形CSAMT三维正演算法在计算三维起伏地形界面处响应的正确性，笔者设计一个三维山峰纯地形模型，并且把场源放置在距离三维地形较远处，以保证测区处于远区，将本文算法的计算结果和三维有限元大地电磁数值模拟算法[7]的计算结果进行对比。

2.1 水平地表三维异常体模型

X轴方向场源，场源中心坐标(-2.4 km,0 km,0 km)；测线在X轴上，在电阻率值为100 Ω·m的均匀半空间中埋藏一个长、宽、高为240 m×120 m×120 m，顶面埋深为100 m，电阻率为10 Ω·m低阻长方体。长方体的中心距离发射场源2.4 km，计算频率为1 000 Hz。模型如图2所示。

分别采用本文算法和水平地表CSAMT三维正演算法[11]利用32位 Windows XP系统台式计算机对图2模型进行数值模拟计算，台式计算机的配置为Intel TM 2.83 GHz 四核处理器、4G内存。2种算法都采用56×58×38(空气层：10)的网格，计算频率为1 000 Hz。图3为频率1 000 Hz时，水平地表三维异常体模型(图2)的本算法(黑色圆圈)和林昌洪等[11](黑色实线)模拟结果的对比图。其中，视电阻率响应的最大误差0.23%，相位响应的最大误差0.28°。

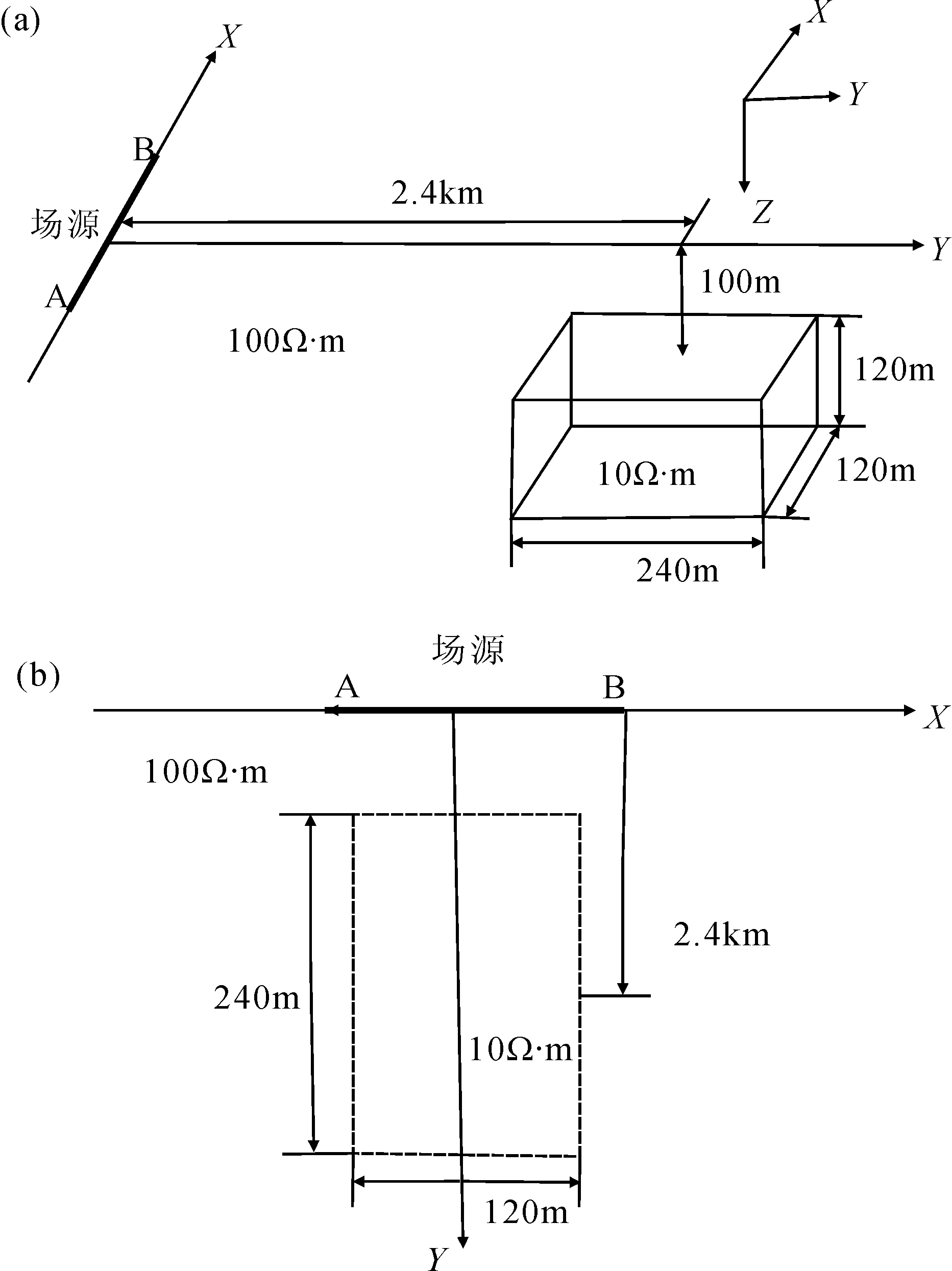
图2 水平地表三维异常体模型(a)异常体模型三维视图；(b) 异常体模型X-Z平面视图 Fig.2 Sketches of the horizontal surface three-dimensional anomalous body model

2.2 三维山峰模型

本文采用Nam等[7]文中的三维山峰纯地形模型，该模型与Wannamaker 等[4]提出的二维经典地形模型类似。模型如图4所示，山峰高度设置为0.45 km(Z轴：-0.45 km和0 km之间)，山顶宽度为0.45 km (X、Y轴：-0.225 km 和 0.225 km之间),山的底部宽度为2 km(X、Y轴：-1 km 和 1 km 之间)，地下介质为电阻率为100 Ω·m的均匀半空间。将坐标原点设于山顶中心，为了让山峰地形处于远区，将一个X轴电偶极子源放置在离山顶中心65 km处(-65 km，0 km，0 km)。

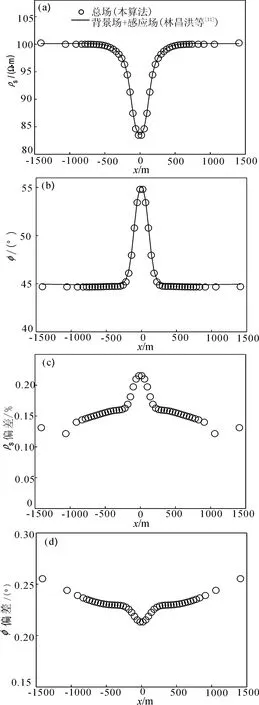
图3 频率为1 000 Hz时水平地表三维异常体模型的本文算法(黑色圆圈)和林昌洪等[11]算法的模拟结果的对比(a)视电阻率；(b)相位响应；(c)视电阻率数值模拟结果误差；(d)相位响应数值模拟结果误差Fig.3 Results of 3D responses at frequency of 1,000 Hz calculated by the forward scheme (black circle) described in this paper(the horizontal surface three-dimensional anomalous body with a X-direction source located at -2.4 km,0 km,0 km) compared with responses calculated by the method given by Lin C H et al[11](black solid line,along the line x=0 m)

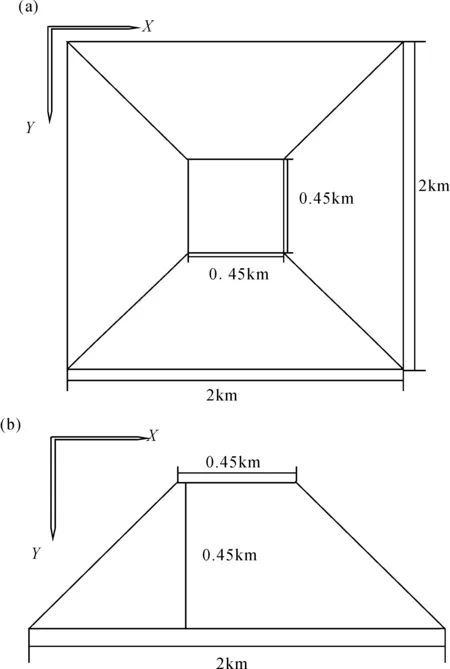
图4 三维山峰地形模型(a) 山峰地形模型X-Y平面图；(b) 山峰地形模型X-Z平面图 Fig.4 Sketches of the three-dimensional trapezoidal-hill models

图5为频率2 Hz 时，本文算法计算的三维山峰模型(图4)的XY和YX模式三维CSAMT视电阻率(图5(a)和(b))和相位(图5 (c)和(d))响应(黑色虚线)与 Nam等[7]算法计算的大地电磁响应(黑色圆圈)的对比图。由于测区位于远区，场源影响小，三维CSAMT结果与大地电磁响应基本一致。图5的结果显示本文有限差分的计算结果和有限元的计算结果吻合得很好，其中，XY和YX模式视电阻率响应的最大误差分别为4.03%、1.335%；相位响应的最大误差分别为0.9°、0.45°，验证了本文提出的带地形CSAMT三维数值模拟算法的准确性。

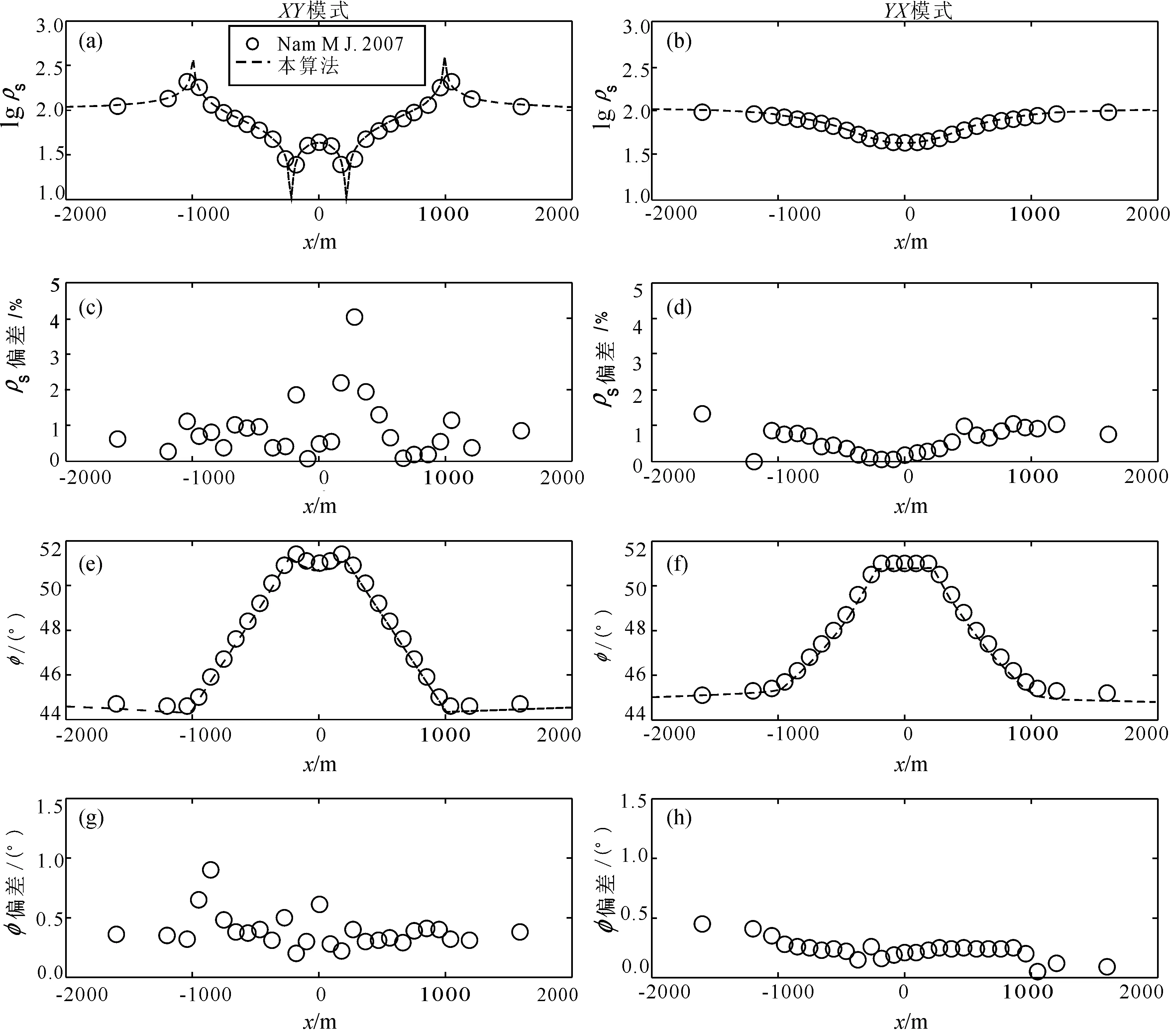
图5 频率2 Hz 时XY和YX模式三维山峰模型(图4)的本算法响应(黑色圆圈)和 Nam等[7]算法计算的大地电磁响应(黑色实线)模拟结果的对比(a)、(b) XY、YX模式视电阻率结果对比；(c)、(d) XY、YX模式两种数值模拟视电阻率结果误差；(e)、(f) XY、YX模式相位结果对比；(g)、(h)XY、YX模式两种数值模拟相位结果误差Fig.5 Comparison of 3D responses (at frequency of 2 Hz) of the method given by this paper (black circle) and 3D FEM MT responses of the method given by Nam et al[7] (black solid line) for models of XY and YX

3 结 论

本文在水平地表三维有限差分CSAMT数值模拟算法的基础上，实现了模拟三维起伏地形CSAMT响应的正演算法。在本算法中，提出了新的由地下交错采样点处的总磁场计算起伏地形下空气-地下介质分界面处电场的表达式；同时，为了避免了原有将总场分离成背景场和二次场的策略在复杂地质条件下难以选择合适背景电阻率构造的问题，引入伪δ函数来代替麦克斯韦方程中的场源项，在三维数值模拟中直接计算总电磁场，从而解决场源奇异性问题；为了三维正演方程可以直接求解总电磁场，将原有的研究边界处二次场值为零的边界条件修改为均匀半空间中电偶极子在远区的一次场值的边界条件，并通过公式推导，获得计算均匀半空间中电偶极子在远区的一次场值的解析表达式。

为了验证本文算法的可靠性，对水平地表三维异常体模型和三维山峰纯地形模型进行了三维数值模拟。采用本文算法模拟得到两个三维模型的视电阻率响应和相位响应，计算结果与前人算法的结果吻合得很好，视电阻率响应的最大偏差小于4.03%，相位响应的最大偏差小于0.9°，验证了本文所实现的起伏地形下三维CSAMT数值模拟算法的正确性。

参考文献：

[1] GOLDSTEIN M A,STRANGWAY D W.Audio-frequency magetotellurics with a grounded electric dipole source[J].Geophysics,1975,40(4)：669-683.

[2] LI Y,KEY K.2D marine controlled-source electromagnetic modeling: Part 1—An adaptive finite-element algorithm[J].Geophysics,2007,72(2)：51-62.

[3] MITSUHATA Y.2-D electromagnetic modeling by finite-element method with a dipole source and topography[J].Geophysics,2000,65(2)：465-475.

[4] WANNAMAKER P E,STODT J A,RIJO L.Two-dimensional topography responses in magnetotelluric modeled using finite elements[J].Geophysics,1986,51(11)：2131-2144.

[5] ZHDANOV M S,LEE S K,YOSHIOKA K.Integral equation method for 3D modeling of electromagnetic fields in complex structures with inhomogeneous background conductivity[J].Geophysics,2006,71(6)：G333-G345.

[6] SASAKI Y.Bathymetric effects corrections in marine CSEM data[J].Geophysics,2011,76(3)： F139-F146.

[7] NAM M J,KIM H J,SONG Y,et al.3D magnetotelluric modelling including surface topography[J].Geophysical Prospecting,2007,55：277-287.

[8] SCHWALENBERG K，EDWARDS R N.The effect of seafloor topography on magnetotelluric fields: an analytical formulation confirmed with numerical results[J].Geophysical Journal International,2004,159：607-621.

[9] WARD S H，HOHMANN G W.Geophysical Electromagnetic Theory,Electromagnetic Method in Applied Geophysics[M].Katris: Society of Exploration Geophysicists,1988:1.

[10] SCHWARZBACH C,BORNER R U,SPITZER K.Three-dimensional adaptive higher order finite element simulation for geo-electromagnetics: a marine CSEM example[J].Geophysical Journal International,2011,187：63-74.

[11] 林昌洪，谭捍东，舒晴，等.可控源音频大地电磁法三维共轭梯度反演研究[J].地球物理学报，2012，55(11): 3829-3838.

[12] 邓居智，谭捍东，陈辉，等.CSAMT三维交错采样有限差分数值模拟[J].地球物理学进展，2011，26(6): 2026-2032.

[13] 雷达.起伏地形下CSAMT正反演研究与应用[J].地球物理学报，2010，53(4):982-993.

[14] 张继锋，汤井田，喻言，等.基于电场矢量波动方程的三维可控源电磁法有限单元数值模拟[J].地球物理学报，2009，52(12): 3132-3141.

[15] 李帝铨,王光杰，底青云，等.基于遗传算法的CSAMT最小构造反演[J].地球物理学报，2008，51(4)：1234-1245.

[16] 陈桂波，汪宏年，姚敬金，等.用积分方程法模拟各向异性中三维电性异常体的电磁响应[J].地球物理学报，2009，52(8)：2174-2181.

[17] 王若，王妙月，卢元林.三维三分量CSAMT法有限元正演模拟研究初探[J].地球物理学进展，2007，22(2)：579-585.

[18] 谭捍东，余钦范，BOOKER John，等.大地电磁法三维交错采样有限差分数值模拟[J].地球物理学进展，2003，46(5)：705-711.