大气土壤耦合的埋地燃气管道泄漏扩散数值分析*

叶 岩，王 岳

(辽宁石油化工大学 石油天然气工程学院，辽宁 抚顺 113001)

0 引言

当前，我国城市燃气泄漏爆炸事故数量仍然偏多，为有效防控燃气泄漏事故风险，需准确评估燃气泄漏事故的扩散范围。国内外学者对燃气管道泄漏致使燃气在大气中的扩散行为进行了较多研究，在气体泄漏模型方面，Holmes等[1]、王大庆等[2]、崔斌等[3]主要通过对气体稳态泄漏模型的研究推导出非稳态泄漏模型的计算方法；在燃气泄漏的实验研究方面，孙立国等[4]、谢昱姝等[5]、Okamoto等[6]主要通过全尺寸实验对燃气泄漏扩散进行了研究，分析燃气在土壤中的对流扩散规律，并验证了Darcy定律在全尺寸地下管道泄漏扩散问题中的适用性；在燃气泄漏的数值模拟方面，李朝阳等[7]、黄雪驰等[8]、张甫仁等[9]主要借助CFD软件对燃气泄漏进行了数值模拟，分析了不同条件对架空管道燃气泄漏扩散的影响。

尽管国内外学者针对气体非稳态泄漏以及扩散行为进行了很多数值分析和模拟研究，但较少考虑到埋地敷设是管道敷设的主要方式[10]，且没有考虑到土壤和大气环境的耦合情况，使得研究缺少实际意义。在土壤和大气环境的耦合方面，Botros等[11]分别为燃气在土壤和大气环境的扩散构建了解析解，并将燃气在地面的扩散通量作为媒介耦合了土壤和大气环境；王岩等[12]基于计算流体力学工具OpenFOAM分别求解甲烷在土壤和大气中的扩散方程，并以地面甲烷通量为媒介进行大气和土壤耦合的数值模拟，分析了地面对流传质系数对地面甲烷通量和街道甲烷浓度测量值的影响；文献[11]和[12]均以地面扩散通量作为媒介耦合土壤大气环境，解决了扩散方程耦合媒介的问题，使得对于以后气体泄漏扩散的研究结果更为贴近实际和准确，但是其仅在理论上进行论证和模拟，没有对忽略耦合时的误差进行研究分析。本文以此为切入点，利用CFD软件针对土壤和大气中燃气扩散的物理规律分别构建控制方程，以LPG主要成分丙烷的地面扩散通量为媒介对土壤和大气环境进行耦合模拟LPG在非稳态泄漏的情况下扩散行为，并针对耦合的埋地泄漏和忽略耦合的地上泄漏两种情况，分析了不同因素对泄漏扩散距离和高度峰值的相对误差的影响。

1 模型建立

已有的研究较少考虑燃气管道埋地敷设的实际情况，而考虑埋地层情况的研究中，很少采用不同物理模型进行大气和土壤环境耦合。本文以此为切入点，采用不同控制方程分别构建大气和土壤的物理扩散模型，进行大气和土壤环境耦合的燃气管道泄漏模拟分析。

1.1 物理模型

1.1.1 物理模型模拟区域

如图1所示，在X，Y，Z方向建立的范围分别是-25～55 m，0～20 m，-40～40 m的模拟区域；建筑物简化为长×宽×高为10 m×10 m×6 m的立方体，底面中心点坐标是(15，1.3，0)；管道埋深1.3 m，泄漏孔位于管道顶部且泄漏孔中心为坐标原点；不考虑土壤环境时，泄漏的物理模型中无埋地层，且其余条件与考虑土壤环境时的泄漏物理模型完全相同。

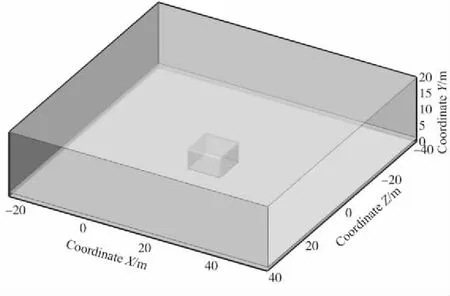
图1 物理模型模拟区域Fig.1 Physical model simulation region

1.1.2 土壤扩散物理模型

根据文献[6]中Darcy定律的土壤渗流，用组分质量分数Ci作为变量的组分输运方程：

(1)

连续性方程如下：

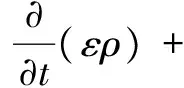
(2)

理想气体状态方程如下：

(3)

式中：vg是气体渗流速度，m/s；ε为土壤的孔隙度；D是气体在土壤中的有效扩散系数；Si是第i个气体组分的质量源项；ρi是第i个气体组分的密度，kg/m3；R是气体常数，取值为8.314；T是温度，K。

1.1.3 大气扩散物理模型

采用可实现k-ε模型求解大气中的气体扩散过程，根据文献[6]的控制方程为：

(4)

(5)

(6)

(7)

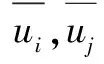
1.2 计算模型

1.2.1 管道大孔泄漏计算模型

燃气管道泄漏时，由于燃气管道不断供气，可认为切断气源之前为稳态泄漏过程，切断气源后为非稳态泄漏过程。泄漏过程中管道内的压力迅速下降，泄漏气体的速度会由音速下降到亚音速，非稳态泄漏阶段由临界流阶段转换到亚临界流阶段，根据文献[2]得到以下非稳态泄漏计算模型。

1)临界流泄漏阶段

(8)

(9)

式中:m0是临界流泄漏阶段初始时刻的管道内的剩余气体的质量，kg；Pa为大气压力，Pa，Pb为临界压力，κ为绝热系数。

2)亚临界流泄漏阶段

(10)

(11)

式中:P为泄漏孔中心压力，Pa；Q为泄漏孔气体质量流量，kg/s；T为泄漏孔处的气体温度，K；下标v2代表亚临界泄漏阶段任意时刻t的物理量；下标v2,0代表亚临界流泄漏初始时刻或者临界流泄漏末时刻的物理量；Ta为初始环境温度，K。

1.2.2 计算模型验证

在赵金辉等[13]以空气为泄漏介质的实验数据的基础上，计算相同实验条件下空气的泄漏速率之后得到表1对比数据：

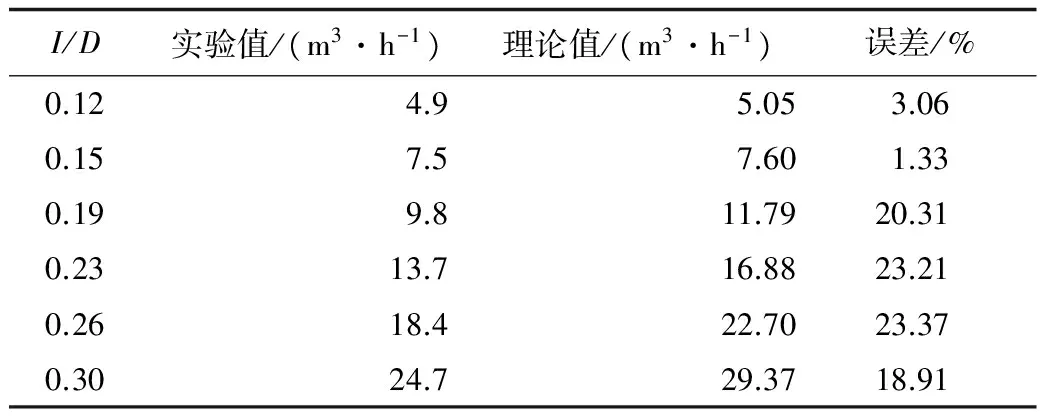
表1 实验值与理论值对比Table 1 Comparison between experimental andtheoretical values

由表1可知，I/D为0.12～0.15时，误差较小；I/D为0.15～0.3时，误差相对较大，但整体处于10%～20%之间，从而验证了计算模型较高的准确性。本文以误差为1.33%的I/D确定泄漏孔径，以提高模拟准确性。

2 计算实例

2.1 实例参数设定

管道内径400 mm，泄漏孔两端阀门相距2 km，泄漏孔径60 mm，管道运行0.7 MPa。LPG组分简化为丙烷85%、正丁烷15%，以丙烷代表LPG进行分析。前30 s为稳态泄漏，30 s关闭阀门后经过57 s进入亚音速泄漏阶段，泄漏过程持续390 s。丙烷的爆炸极限为2.1%～9.50%，取质量分数为2.47%和11.1%为模拟区域的可爆炸范围的分界浓度。

2.2 初始条件和边界条件设置

泄漏孔为质量流量入口；x轴负方向为风速入口；x轴正向、顶面和侧面为压力出口；土壤设为多孔介质并添加阻力源项；土壤和大气交界面添加多孔介质跃迁层来耦合由土壤进入大气的丙烷通量，以完成丙烷由土壤扩散转向大气扩散的耦合过程，即以丙烷从土壤扩散到大气与土壤交界面的通量为源项继续丙烷在大气扩散的模拟；底面为不透气边界。

2.3 模拟结果分析及讨论

2.3.1 实际条件下的模拟结果

图2-5所示为实际条件(风速1 m/s，温度300 K，相对湿度20%)的模拟结果。埋地泄漏时由于土壤的惯性阻力和粘性阻力，丙烷通过埋地层时损失大量能量，以致其竖直扩散范围明显降低，水平扩散范围明显增大。图2-5的(a)，(b)和(c)依次为t=30 s,t=87 s和t=150 s时各切面的丙烷浓度云图，依次表示稳态泄漏阶段末、临界流泄漏阶段末和亚临界流泄漏阶段；稳态泄漏阶段(0～30 s)，埋地泄漏时丙烷主要在埋地层中扩散且由于壁面摩擦等因素使得建筑物底部有较高浓度的丙烷，一部分丙烷通过地面后在大气中扩散，由于燃气中不同分子质量气体分子的相互作用而发生偏移[14]；地上泄漏时，丙烷所受空气阻力较小，向上喷射后形成超过模型高度(20 m)的典型喷射流。临界流阶段(30～87 s)，埋地泄漏的泄漏量较大，丙烷在重力作用下聚集在地面，扩散范围接近圆形；而地上泄漏时，其扩散高度依然超过模型高度。亚临界流阶段(87～390 s)，埋地泄漏的泄漏速度较低，泄漏量与临界流阶段相比下降，150 s之后扩散范围基本稳定；地上泄漏扩散高度随泄漏过程进行而下降，150 s之前地面丙烷浓度基本均低于2.47%。本文之后的模拟主要分析2种模型丙烷扩散范围的变化趋势，丙烷的浓度云图便不再累述。

2.3.2 风速对丙烷扩散的影响

如图6所示：埋地泄漏时，低风速促进丙烷的水平扩散，而高风速则在较短的时间内使丙烷的危险范围达到峰值后降低其危险范围，且危险范围到达峰值的时间、泄漏过程结束时的扩散范围与风速成反比。地上泄漏时，丙烷水平扩散距离在稳态泄漏阶段迅速降低、临界阶段基本稳定，经过一段时间的稳定之后，其缓慢增大直至相对稳定，且过程中稳定时间、扩散范围与风速成反比；埋地泄漏丙烷的扩散高度在短时间内达到峰值之后缓慢降低且泄漏过程中的最大高度随风速的增加先增后减。地上泄漏丙烷的扩散高度在极短时间内超过模型最大高度，经过一段时间扩散高度降低到20 m以下且超过20 m的时间与风速成反比。两种模型的泄漏在高度方向均在过程结束时达到稳态且高度相差不大。

图2 埋地泄漏的Z=0 m平面Fig.2 The Z=0 m plane of the buried leaking

图3 地上泄漏的Z=0 m平面Fig.3 The Z=0 m plane leaking on the ground

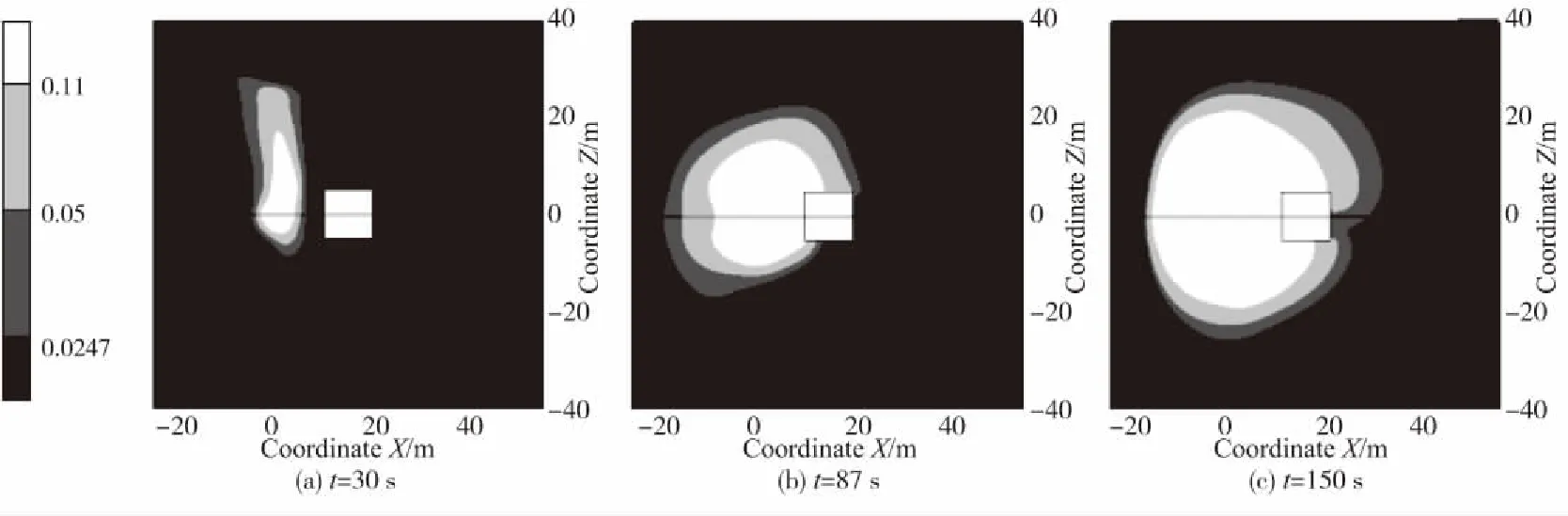
图4 埋地泄漏的Y=1.3 m平面Fig.4 The Y=1.3 m plane of the buried leaking

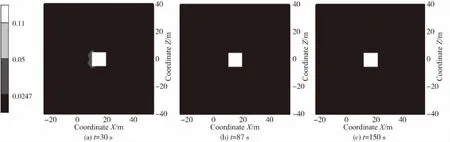
图5 地上泄漏的Y=1.3 m平面Fig.5 The Y=1.3 m plane leaking on the ground

以埋地泄漏扩散距离为基准，对比地上泄漏与埋地泄漏的相对误差。由表2可知，泄漏过程中，水平扩散距离的相对误差在风速为1 m/s时最小，值为7.04%，其余风速条件下，相对误差均较高，且在风速为5 m/s时达到41.4%；竖直扩散高度的相对误差在风速为3 m/s时最小，但同样超过66.7%，其余风速条件下，其值均在100%以上。因此，在风速的影响下，地上泄漏相对于埋地泄漏，水平扩散范围有相当大的误差，对事故的预测和评估准确性会产生显著影响。

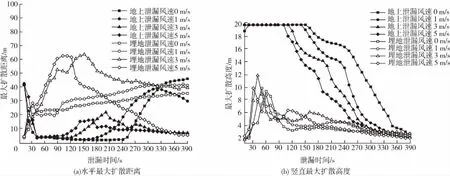
图6 风速对丙烷扩散的影响Fig.6 Effect of wind speed on propane diffusion

泄漏类型及相对误差风速0m/s风速1m/s风速3m/s风速5m/s扩散距离/m扩散高度/m扩散距离/m扩散高度/m扩散距离/m扩散高度/m扩散距离/m扩散高度/m埋地泄漏36．09．549．210．064．012．063．010．0地上泄漏46．5≥2039．6≥2042．6≥2036．9≥20相对误差/%29．2≥1117．04≥10033．4≥66．741．4≥100

2.3.3 温度对丙烷扩散的影响

以253K，283K和300K分别代表冬季、春秋和夏季的环境温度，结果如图7所示：埋地泄漏时，水平扩散范围在较短时间内迅速增加之后基本稳定，稳定高度随温度的升高而降低；竖直方向上，温度只对全过程中最大高度的峰值有较为明显的影响——随温度的增高先增后减。地上泄漏时，水平方向上不同温度的扩散变化趋势基本相同，夏季的扩散范围在泄漏过程中后期较春秋和冬季有较大的增加；竖直方向上，不同温度的扩散超过20 m高度的时间基本相同，之后缓慢下降且泄漏过程结束时扩散高度随温度的增加降低。

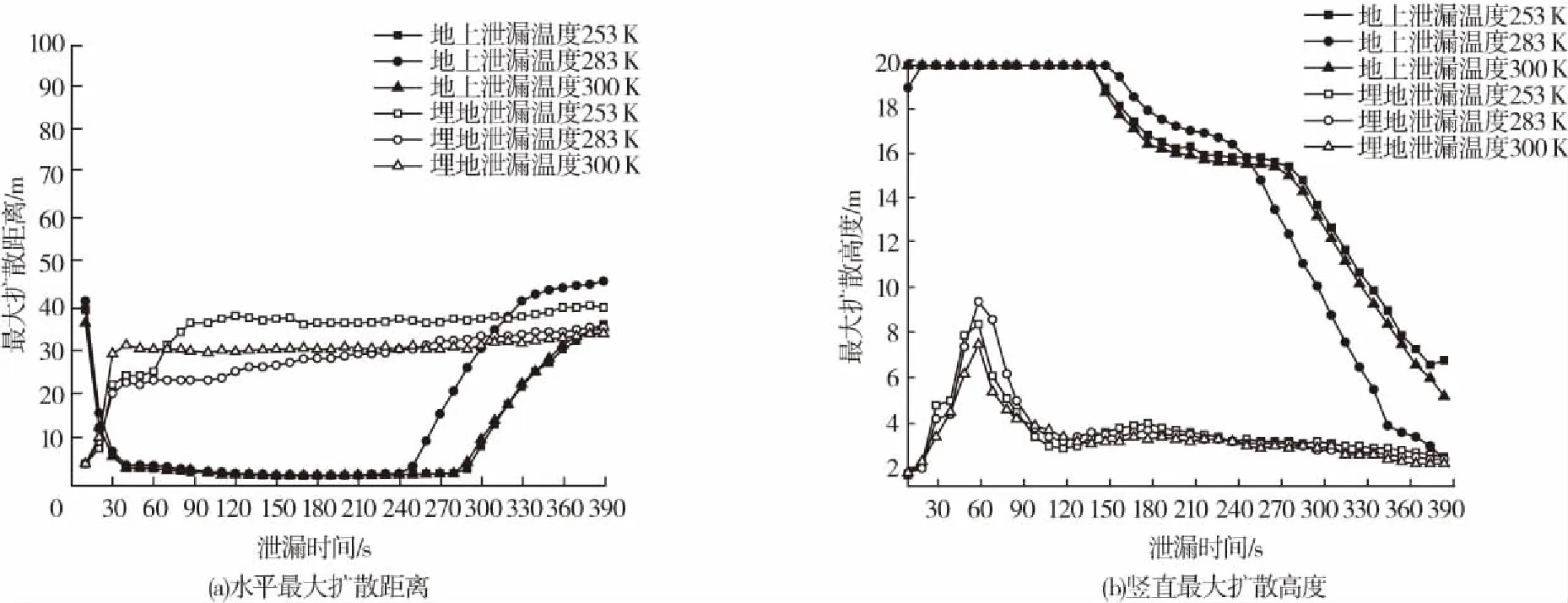
图7 温度对丙烷扩散的影响Fig.7 Effect of temperature on diffusion of propane

由表3可知：整个泄漏过程中，水平方向扩散距离相对误差在温度为300 K时最大，值为29.2%，其余条件下值较低且在5%以下；竖直方向的相对误差在温度为300 K时最小，但同样超过111%。因此，在不同温度(或季节)的影响下，地上泄漏距离相对于埋地泄漏在300 K(或夏季)时有相对较大的误差，而在泄漏高度上均相当大的误差，较大程度上的影响了预防和评估的准确性。

表3 不同温度条件下地上泄漏和埋地泄漏峰值的相对误差Table 3 Relative error of the peak leakage and burying leakage at different temperatures

2.3.4 相对湿度对丙烷扩散的影响

如图8所示：埋地泄漏时，水平扩散距离随相对湿度的增加均在稳态泄漏阶段迅速增长、在非稳态泄漏阶段缓慢增长，总体上扩散距离随着相对湿度的增加而增加且幅度较小；竖直方向上，随湿度的增加，泄漏过程中丙烷所能达到的高度峰值降低，在120 s之后扩散高度下降速度基本相同且稳定。地上泄漏时，不同相对湿度的水平扩散距离在220 s之前扩散趋势基本一致，之后扩散距离迅速增加，总体上扩散距离随相对湿度的增加而增加；竖直方向上，不同相对湿度条件下，最大扩散高度超过20 m所需时间基本相同，扩散高度的下降趋势和高度也基本相同。

图8 相对湿度对丙烷扩散的影响Fig.8 Effect of humidity on diffusion of propane

由表4可知：泄漏过程中，水平方向扩散距离的相对误差在相对湿度为50%时最大，为57.7%，其余相对湿度条件下，2种模型水平方向扩散距离的误差均在30%以下；竖直方向泄漏高度的相对误差在相对湿度为0%时最小，但同样超过111%，而在相对湿度为20%时超过203%。因此，在不同相对湿度的影响下，地上泄漏距离相对于埋地泄漏距离在3个相对湿度范围内均有较大的误差，在泄漏高度上均相当大的误差，对事故后果预测和评估的准确性有显著影响。

表4 不同相对湿度条件下地上泄漏和埋地泄漏峰值的相对误差Table 4 Relative error of the peak leakage and burying leakage at different relative humidity

3 结论

1)考虑土壤环境和大气环境的耦合时，风速是影响丙烷扩散距离和高度的主要因素，低风速能稳定地促进丙烷的扩散，高风速则先促进扩散后抑制扩散；温度的升高对丙烷的扩散距离有先促进后抑制的作用，而对扩散高度有抑制作用；相对湿度的增加对扩散距离有稳定的促进作用，而对扩散高度有稳定的抑制作用。

2)随着风速的增大，地上泄漏和埋地泄漏2种情况下，其水平扩散距离的差值先减小后增大，且差值相对较大；在较低温度下，地上泄漏和埋地泄漏的水平扩散距离相对误差很小，而在较高温度下，相对误差较大；在相对湿度较低时，地上泄漏和埋地泄漏情况下水平扩散距离的数值相对较大，但相对误差较为稳定，而在相对湿度较高时，相对误差很大。

3)在不同风速、温度和相对湿度的条件下，地上泄漏与埋地泄漏相比，其对应扩散高度普遍偏大，这将导致在不考虑埋地泄漏时对泄漏燃气的扩散高度预测偏高，同样会对事故后果预测和评估的准确性产生显著影响。

[1] HOLMES N S, MORAWSKA L. A review of dispersion modelling and its application to the dispersion of particles: an overview of different dispersion models available[J]. Atmospheric environment, 2006, 40(30): 5902-5928.

[2] 王大庆, 张鹏. 压力容器气体非稳态泄漏模型研究[J]. 中国安全科学学报, 2012, 22(7):154-158.

WANG Daqing, ZHANG Peng. Non-steady-state gas leakage model for pressure vessel failure[J]. China Safety Science Journal, 2012, 22(7):154-158.

[3] 崔斌, 韦忠良. 燃气管道非等温非稳态泄漏模型[J]. 油气储运, 2010, 29(1):36-37, 40.

CUI Bin, WEI Zhongliang. Nonisothermal and unsteady state leakage model for gas pipelines[J].Oil & Gas Storage and Transportation, 2010, 29 (1) 36-37, 40.

[4] 孙立国,周玉文. 埋地燃气管网泄漏规律及其次生灾害预防研究[J]. 煤气与热力,2010,30(1):38-42.

SUN Liguo, ZHOU Yuwen. Study on leakage rule of buried gas pipeline and prevention of secondary disasters[J].Gas & Heat,2010,30(1):38-42.

[5] 谢昱姝, 吴宗之, 吕良海,等. 城市管道天然气在土壤中泄漏扩散实验研究[J]. 中国安全生产科学技术, 2012, 8(4):13-17.

XIE Yushu,WU Zongzhi ,LYU Lianghai，et al. Experimental research on diffusion behavior of leaked gas from underground gas pipeline[J].Journal of Safety Science and Technology,2012, 8(4):13-17.

[6] OKAMOTO H, GOMI Y. Empirical research on diffusion behavior of leaked gas in the ground[J]. Journal of Loss Prevention in the Process Industries, 2011, 24(5):531-540.

[7] 李朝阳, 马贵阳. 埋地与架空输气管道泄漏数值模拟对比分析[J]. 天然气工业, 2011, 31(7):90-93.

LI Zhaoyang, MA Guiyang. A comparative study of numerical simulation on underground and aerial pipeline leakage at instantaneous and continuous states[J]. Natural Gas Industry, 2011, 31(7):90-93.

[8] 黄雪驰, 马贵阳, 杨奇睿,等. 天然气管道非稳态泄漏扩散的数值模拟[J]. 安全与环境学报, 2017,17(1):183-188.

HUANG Xuechi, MA Guiyang, YANG Qirui, et al. Numical simulation of unsteady leakage and diffusion of the gas pipeline[J]. Journal of Safety and Environment, 2017,17(1):183-188.

[9] 张甫仁, 徐湃. 燃气管道非稳态泄漏及扩散的模拟[J]. 哈尔滨工业大学学报, 2009,41(5):201-204.

ZHANG Furen, XU Pai. Numerical simulation of unsteady leakage and diffusion of gas pipeline [J]. Journal of Harbin Institute of Technology, 2009,41(5):201-204.

[10] 李军, 张宏, 梁海滨,等. 基于模糊综合评价的燃气管道第三方破坏失效研究[J]. 中国安全生产科学技术, 2016, 12(8):140-145.

LI Jun，ZHANG Hong，LIANG Haibin, et al. Study on failure of gas pipeline due to third party damage based on fuzzy comprehensive evaluation[J]. Journal of Safety Science and Technology, 2016, 12(8):140-145.

[11] BOTROS K K, ENNIS C J, ZhOU J, et al. Prediction of gas transport through ground and atmosphere to determine the ability of airborne leak detection methods to detect pin-hole leaks from buried gas pipelines[C]// International Pipeline Conference-2008. 2009:11-28.

[12] 王岩, 黄弘, 黄丽达,等. 土壤大气耦合的燃气泄漏扩散数值模拟[J]. 清华大学学报(自然科学版), 2017,57(3):274-280.

WANG Yan, HUANG Hong, HUANG Lida，et al. Numerical simulations of leakage gas dispersion based on soil and atmosphere coupling[J].Journal of Tsinghua University(Science and Technology),2017,57(3):274-280.

[13] 赵金辉, 谭羽非. 燃气管线大孔亚临界流泄漏实验[J]. 哈尔滨工业大学学报, 2011, 43(2):84-87.

ZHAO Jinhui，TAN Yufei. Experiment study on subcritical flow nozzle model in the gas pipelines[J]. Journal of Harbin Institute of Technology, 2011, 43(2):84-87.

[14] 王冠培, 郭开华, 潘国君. 基于CFD的天然气管道混气扩散规律研究[J]. 热科学与技术, 2015,14(6):484-491.

WANG Guanpei，GUO Kaihua，PAN Guojun. Research on natural gas pipeline mixing-flow properties based on computational fluid dynamics[J]. Journal of Thermal Science and Technology, 2015,14(6):484-491.