武汉市轨道交通线网应急救援站选址研究*

冉连月，吴贤国，刘 洋，张立茂

(1.华中科技大学 土木工程与力学学院，湖北 武汉 430074； 2.武汉大学 中南医院，湖北 武汉 400071)

0 引言

随着城市的不断发展，其规模逐渐扩张，人口不断增长，为了解决城市空间容量以及功能不足、交通堵塞、生活空间严重缺乏等一系列城市问题，可采取的有效措施就是加大对地下空间合理充分地开发利用和依据城市规划合理建设城市轨道交通，城市轨道交通在城市发展中扮演着越来越重要的角色。然而，城市轨道交通网络化的迅猛发展也会产生一些问题，以地铁为例，地铁在通常情况下都是位于地下的完全封闭空间或者类似高架桥的半封闭空间里，具有其他公共场所没有的独特特性，地铁空间里不仅人员集中，且封闭、设备密集，若发生较为严重的突发事件，封闭空间里集中的人员必然不容易被疏散，且应急救援也不易快速进行，稍有不慎将会对人们的生命和财产造成巨大损失。此外，在如今轨道交通网络化运营的前提下，各种轨道交通线网中的突发事件往往不仅是一个简单的孤立事件，其影响在很大程度上会波及到其他线路甚至城市整个轨道交通系统。因此，为应对轨道交通线网可能发生的突发事件，建立轨道交通线网应急救援站具有重要意义。

目前，国内外针对复杂网络应急救援站的选址与优化有了初步的研究。在国外，德国学者Weber对于仓库位置的研究，开启了选址研究以及优化的开端[1]；1998年，Badri等利用整数目标规划的方法，建立了多目标选址模型，同时也把这个方法应用到消防站的选址问题上[2];Ogryczak也在研究中给出了一个对于应急救援站选址的双目标模型，这是一个考虑到全部相关距离的多目标分布模型[3]；在国内，刘浪等利用加权网络，对应急物资储备点的选址进行详细研究分析，既考虑了建设成本，也考虑到整个线网系统的稳定性[4]；钱明军等基于复杂网路，建立了城市公交枢纽选址的评价体系，最终得到具有较好可行性的选址结果[5]。总结目前已有研究成果，国内对选址方面问题虽然有一定的研究，但针对一个实际具体城市的轨道交通线网进行应急救援站选址研究还较少。武汉作为我国中部地区的核心城市，近些年发展迅速，目前其轨道交通线网处于发展阶段，但尚没有建立相应的应急救援站，其应对突发事件的救援能力较弱。因此，立足于武汉市轨道交通网络化的背景，引入网络科学的相关理论，对武汉城市轨道交通网络的应急救援站选址进行研究，具有重要的研究价值和现实意义。

1 P-中心应急救援站选址模型建立

1.1 P-中心模型定义

P-中心模型是一个进行选址问题研究的基本模型，它解决的问题是在应急救援站点数目一定的情况下，合理地布置p个应急救援站的位置，使所有需求站到离它最近的应急救援站的距离中的最大距离最小。P-中心模型在理论上，就是让选址结果能出现的最坏情况变得最好，故常把此模型当作极小化极大模型或者比作“经济平衡性”模型，其最优目标值就是P-半径。因为在轨道交通线网应急救援站选址研究中，对于救援的时效性会给予很大的重视，而P-中心模型就需要尽可能的缩小应急救援站与需求站间距离，故可以把城市轨道交通线网应急救援站选址研究问题，当作一个P-中心模型问题来分析。

1.2 应急救援站选址模型建立

运用复杂网络[6]理论，将轨道交通线网当作一个复杂网络，其中各个车站就是网络中的各个节点，节点之间的边就是车站之间的线路。假设有m个车站，它们都是潜在的突发事件事故点，所以应急救援需求点的集合就是U={u1,u2,...,um}；应急救援站备选点集合为V={v1,v2,...,vn}⊂U，备选点集合当中的节点和数量n可以根据不同情况而定，而P-中心模型的p个应急救援站将在这n个节点中选取产生。根据复杂网络的网络中心性特点，特殊站点可以先选出网络的重要节点作为应急救援站的必设点，设必选点集合P={vn1,vn2,...,vnt⊂V⊂U，这些必设点被默认设置为应急救援站，那么就还需要在备选点集合V中选出(p-t)个节点来设置应急救援站。因此，这个P-中心选址问题就是在完全图G=(U,E)中找1个设定的集合X⊆V，使得Z最小，Z的定义如下：

(1)

式中：X集合即是这个应急救援站选址问题的解，个数为p；d(ui,vj)为应急救援站备选点vj到应急救援需求点ui的路径距离。

选址问题用整数规划模型描述如下。

目标函数：Min(Z)

(2)

约束条件：

(3)

式中，前2个结束为空间约束条件，中间2个结束为成本约束条件，最后2个结束为救援约束条件。

2 武汉市轨道交通线网应急救援站的选址

2.1 网络中心性分析

为了能够在网络中考虑选址问题，首先需要把武汉市轨道交通线网进行网络化描述，形成1个无向图G=(E，V)。截至2017年7月，武汉市轨道交通运营线路总长185.65 km，共有6条(包含机场线)线路、126座车站，其中换乘车站13座，对应着无向网络图G=(E，V)中的126个节点和133条边。为每个节点编号，得到最终的网络化应急建模无向图，如图1所示。

图1 武汉市轨道交通线网网络化应急建模无向图Fig.1 Undirected graph of networked emergency modeling of rail transit network in Wuhan

网络中心性分析中，重要的2个指标分别是节点度[7]和介数值[8]，计算出各个节点的度值和介数值并进行排序，就可以找到网络的网络中心。图1节点形状大小就是与介数值大小相对应的，介数值越大，节点越大。其中节点度值最高为4，包括节点：V12,V86,V45,V69,V39,V17,V64,V20,V13；度值为3的节点包括：V7,V8,V76,V23；介数值排名前10的点依次为：V12,V39,V45,V8,V17,V69,V64,V11,V10,V86。网络中心性分析的目的是找出轨道交通网络的网络中心，以确定应急救援站备选点集合和必选点集合。鉴于城市轨道交通网络相对一般意义上的复杂网络规模较小，完全利用网络中心来确定网络中的重要节点有一定的局限性，所以根据城市轨道交通网络的实际情况，还需要根据应急救援站选址中的时间最短、成本节约以及救援站接近车辆段等原则共同来选定这2个集合中的节点。

首先，需要确定必选点集合P的选定，通过网络中心性分析可知，网络中的最高度为4，有9个节点，它们连接多条线路，都是网络中“流量”较高的节点，具有较大的影响力，原则上都应设为必选点，但是V12、V13、V45这3个节点相邻，必选点集合中的节点应尽量分散布置，因此在这3个节点选择介数值最大的节点V12作为必选点，V13、V45作为备选点即可。同理，V39、V69相邻，选择介数值较大的V39作为必选点，V69作为备选点。V64、V17不相邻，但中间只隔1个节点，十分相近，介数值大小也相近，根据分散原则选择距离必选点V39、V20更远的V64作为必选点，V17作为备选点。同时，V20、V86作为最高度的节点被选为必选点。V23虽然介数值排名不在前20位，但该站设有车辆段，且是换乘站，所以把该节点设为必选点。另外，V56和V102虽然度值为1，介数值也很低，但这2个节点是停车场(车辆段)，也处在轨道交通系统的边缘，这样的站点如果由其他应急救援站来覆盖，势必会加大救援距离，降低救援效率，所以，这2个节点也设为必选点。最终得到的应急救援站必选点集合P={V12,V20,V23,V39,V56,V64,V86,V102}，共8个节点，分别对应的车站是江汉路站、常青花园站、宏图大道站、宗关站、汉口北站、香港路站、钟家村站和武汉火车站站。

应急救援站备选点集合V由度大于或等于2的换乘站节点和介数值较高的节点共同构成，集合的大小以基本能覆盖整个网络为宜。另外，根据备选点选取原则，集合V还包含设有车辆段或停车场、附近有车辆段或停车场、火车站或购物中心等人流集散点节点和因为其他一些特殊情况需要考虑作为备选点的节点。

最终得到的应急救援站备选点集合V={V1,V7,V8,V9,V10,V11,V12,V13,V17,V18,V20,V22,V23,V28,V34,V39,V41,V45,V46,V56,V64,V66,V67,V68,V69,V73,V76,V78,V85,V86,V90,V102,V103,V111,V121}，共35个节点。

2.2 模型的应用与求解

上文构建的应急救援站P-中心选址整数规划模型，应用到武汉市轨道交通网络中，经过分析以及计算,得到参数如下：

1)线网所有站点集合U中，元素个数m=126。

2)线网备选点集合V中，元素个数n=35。

3)线网必选点集合P中，元素个数t=8。

4)线网应急救援站站点数p的上、下限分别就是n和t，故其具体范围区域为[8，35]。

5)轨道交通线网网络的最短路矩阵dij=d(ui,vj)由floyd算法编程得到。

整理得到参数后，需要对模型进行求解，求解的方法有多种，如：解析方法、最优化方法、启发式方法、遗传算法等，为了在求解后得出更优的城市轨道交通网络应急救援站布局，本文选用全局搜索优化、运算速度快的遗传算法对模型进行求解[9]。其步骤流程为：形成初始种群→计算适应度→找出算子→交叉算子→变异算子→终止，通过此流程进行求解，即可输出需要的最佳近似解。

2.3 遗传算法运行结果分析

P-中心问题最终得出的最优解是一个近似值，而且遗传算法初始种群的产生是有一定的随机性的，不一样的初始种群，使得程序得到的运行结果也都不一样，所以，需要通过程序进行若干次运行，最终得到相对的最优解。同时，为了成本节约，p数量需要尽量小，从不同运行结果中选择出最好结果，具体的运行结果如表1所示。

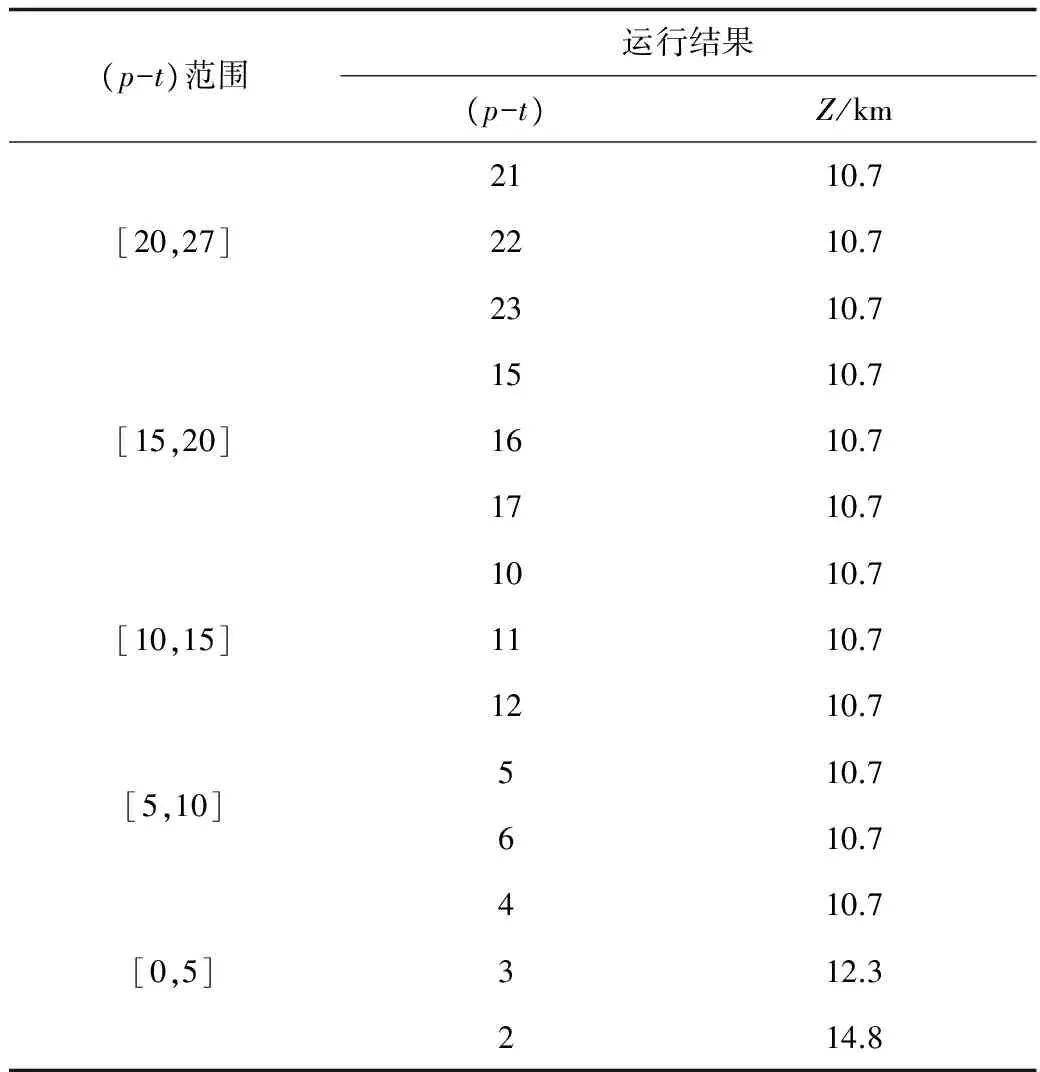
表1 程序运行结果Table1 Program running results

由表1可知，根据已选好的必选点与备选点，可得到的最好的结果是Z=10.7，即在轨道交通线路网络图中，所有的救援距离中最大的距离是10.7 km，同时，救援站的总数p在上升时，Z也就在减小，当备选点中(p-t)值增加到4(即总数p值是12)时，Z能够达到理想中的最优值10.7，如若p值再次增加，Z值也不会再次发生变化。

所以，通过综合考虑到优化目标值与节省成本值2个方面，最终确定的结果为：(p-t)=4，Z=10.7。根据程序最终的运行结果，其最终实际情况是，武汉轨道交通线网应急救援站总数为p=8+4=12座，即应急救援站集合为X={V8，V12，V20，V23，V28，V34，V39，V56，V64，V76，V86，V102}，对应的车站分别是洪山广场站、江汉路站、常青花园站、宏图大道站、天河机场站、古田一路站、宗关站、汉口北站、香港路站、东风公司站、钟家村站、武汉火车站站。应急救援距离中的最大值Z=10.7 km，是应急救援点V34(古田一路站)到需求点V126(径河站)的距离，所以应急救援站在轨道交通线网中分布情况如图2所示。

图2 武汉轨道交通线网应急救援站最终布置方案Fig. 2 Final layout plan of Wuhan rail transit network emergency rescue station

3 武汉轨道交通线网脆弱性分析

3.1 轨道交通线网攻击模拟

通过网络中心性分析以及遗传算法优化得到武汉轨道交通线网应急救援站的最终布置方案，应急救援站在轨道交通线网中起着重要的作用，然而城市中可能出现的各种突发事件可使轨道交通网络站点以及线路瘫痪，如出现自然灾害、车辆故障等情况。应急救援站能够对线网其他遇到危险事故的需求站进行救援，然而，当应急救援站本身遭到攻击时，若其失去救援能力，则会造成严重的损失与影响，故在此对设定的12个应急救援站进行攻击模拟，对武汉轨道交通线网进行脆弱性分析[10]，因为度值越高、介数越高的节点的重要性和影响力都较大，故结合对度值靠前的12个节点以及介数值靠前的12个节点模拟攻击的结果进行对比，分析应急救援站选址的可靠性与脆弱性。

脆弱性是一种面对外来或者内在影响扰动而使系统结构破坏或丧失某些功能的一种反应属性[11]，针对轨道交通线网，其脆弱性则可定义为线网的节点受到攻击后影响整个网络全局效率下降的程度。一般攻击形式包括：随机攻击、单个节点蓄意攻击和累积节点蓄意攻击[12]，其中累积节点蓄意攻击因持续攻击网络中选择的重要节点，对整个线网的影响最大，线网性能的敏感程度最大，故选择累积节点蓄意攻击进行攻击模拟。

3.2 轨道交通线网脆弱性指标

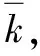
(4)

D=max{dij}

(i=1,2,...,n,j=1,2,...,n,i≠j)

(5)

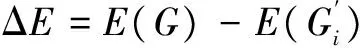
(6)

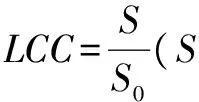
S0为网络初始节点数目)

(7)

3.3 轨道交通线网脆弱性分析

基于上文建立的武汉市轨道交通线网网络化应急建模无向图，按累积节点蓄意攻击模式对此轨道交通线网进行攻击模拟，分析各个指标在各个节点受到持续攻击过程发生的变化，通过不同节点的攻击模拟对比，可对轨道交通线网进行脆弱性评价分析。

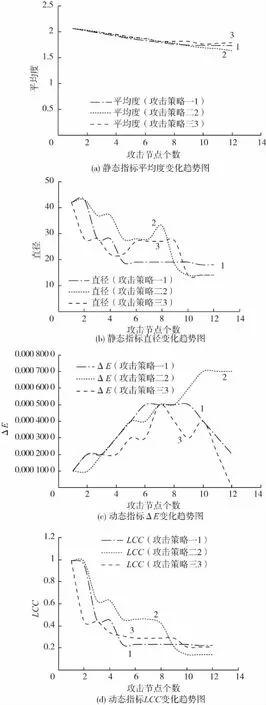
图3 3种攻击策略下各指标变化趋势Fig 3. Trends of various indicators under three attack strategies

首先，对选择的12个应急救援站进行模拟攻击，按度的大小，从大到小顺序进行攻击，故先对度值为4的V12、V20、V39、V64、V86 5个节点进行随机攻击，然后重新计算度值，对度值最大的节点继续进行攻击，直到攻击完12个节点，此为攻击策略一；然后，重新选择度值大小排序前12的节点，按度值由大到小进行攻击，此为攻击策略二；最后，再重新选择介数值排序前12的节点，按介数值由大到小进行攻击，此为攻击策略三。攻击过程中，各指标变化趋势如图3所示。4个指标曲线具体分析如下。

1)平均度曲线分析：由图3(a)可知，在受到累积节点的蓄意攻击后，线网的平均度和直径都在下降，平均度在攻击策略二中下降最快，攻击策略一中下降较缓，说明所选12个应急救援站受到攻击后还能保持较高的密集程度，由于攻击策略三种攻击的是介数值最高的12个点，这12个点中有许多点是相连接的，所以对它们的攻击也能使线网保持较高的密集程度。

2)直径曲线分析：线网直径是反映线网连通性的1个指标，若节点数不变，则直径越大，连通性越差，然而当遭到攻击后，线网被割裂为几个小线网，各部分线网直径减小，整体连通性减弱，最大直径越小，说明被攻击遭到的破坏越大，而从图3(b)中可以看出，最终直径保持最大的是攻击策略一中的曲线，说明这种攻击对整体线网连通性的破坏最小。

3)ΔE曲线分析：由图3(c)中可知，攻击策略一和攻击策略三中，ΔE变化曲线较一致；而攻击策略二中，曲线最终值趋大，说明线网受到破坏大，线网脆弱性大。

4)LCC曲线分析：LCC(最大连通子图比率)是评价线网整体连通性的动态指标，节点受到攻击后LCC会逐渐变小，如果最终值变得越小，说明整个线网收到的攻击破坏越大，从图3(d)中可以看出，攻击策略一中，LCC曲线的最终值最大，这说明其受到的攻击破坏最小，显示应急救援站对整个线网脆弱性增强的贡献较大。

综上分析，对所选的12个应急救援站进行模拟攻击与对度值最高的12个点以及介数值最高的12个点进行模拟攻击相比，应急救援站更能使整体线网保持稳定性，使破坏降到最小，具有最小脆弱性。

4 结论

1)根据应急救援站选取原则以及空间、成本、救援3个方面的约束条件，建立P-中心应急救援站选址模型，其中基于网络中心性在城市轨道交通网络中选出p个应急救援站的必选点。

2)针对武汉市轨道交通线网进行应急救援站选址分析，对该城市线网进行网络中心性分析，从而选出武汉城市轨道交通线网的8个应急救援站必选点。通过遗传算法在matlab平台上进行编程求解，从备选点集合中选取了4个点作为应急救援站，最终选取12个应急救援站。

3)通过对武汉轨道交通线网的攻击模拟进行脆弱性分析，分3次不同的累积节点蓄意攻击策略来进行，分别是对选取的12个应急救援站、度值前12的站点、介数值前12的站点分别进行攻击，通过脆弱性对比分析得出，选取的12个应急救援站脆弱性最小，说明选址方案可靠。

[1] BRANDEAU M L, CHIU S S. An overview of representative problems in location research[J]. Management Science, 1989, 35(6):645-674.

[2] BADRI M A, MORTAGY A K, ALSAYED C A. A multi-objective model for locating fire stations[J]. European Journal of Operational Research, 1998, 110(2):243-260.

[3] OGRYCZAK W B. On the distribution approach to location problems[J]. Computers & Industrial Engineering, 1999, 37(3): 595-612.

[4] 刘浪，黄有方，逄金辉.加权网络应急物资储备点选址方法[J].北京理工大学学报，2011，31(2)：244-248,252.

LIU Lang, HUANG Youfang,PANG Jinhui. Method for selecting the location of a weighted network emergency material reserve point[J]. JOURNAL OF BEIJING INSTITUTE OF TECHNOLOGY,2011, 31(2): 244-248,252.

[5] 钱明军，万亦强.基于复杂网络的城市公交枢纽选址研究[J].科技资讯，2012(12)：243-244.

QIAN Mingjun,WAN Yiqiang. Research on Location Selection of Urban Transit Hub Based on Complex Network[J]. Science Bulletin, 2012(12): 243-244.

[6] 汪小帆，李翔，陈关荣.网络科学导论[M].北京：高等教育出版社，2012.

[7] FREEMAN R D, LAI C E. Development of the optical surfaces of the kitten eye[J]. Vision Research, 1978, 18(4):399-407.

[8] FREEMAN L C. A set of measures of centrality based on betweenness[J]. Sociometry, 1977, 40(1):35-41.

[9] 李刚.基于网络中心性的城市轨道交通应急救援站选址研究[D].北京：北京交通大学，2014.

[10] 刘亮，韩传峰，缪莉莉，等.基于中心性的工程承包商合作网络脆弱性仿真[J].土木工程与管理学报，2013(1)：62-66.

LIU Liang,HAN Chuanfeng,MIAO Lili,et al. Centralized vulnerability simulation of cooperation network of engineering contractors[J]. Journal of Civil Engineering and Management,2013(1):62-66.

[11] 李鹤，张平宇，程叶青.脆弱性的概念及其评价方法[J].地理科学进展，2008，27(2)：18-25.

LI He, ZHANG Pingyu,CHENG Yeqing.The concept of vulnerability and its evaluation method[J]. Advances in Geography,2008 ,27(2): 18-25.

[12] 李冰玉，秦孝敏.城际铁路线网站点及线路的脆弱性分析[J].中国安全科学学报，2013(5)：108-113.

LI Bingyu, QIN Xiaomin. Analysis of the vulnerability of sites and lines of intercity railway lines[J]. China Safety Science Journal,2013(5): 108-113.

[13] 吴贤国, 黄艳华, 刘惠涛,等. 基于复杂网络理论的地铁线网脆弱性分析[J]. 重庆交通大学学报:自然科学版, 2016, 35(4):93-99.

WU Xianguo,HUANG Yanhua,LIU Huitao,et al.Vulnerability analysis of subway line network based on complex network theory[J]. Journal of Chongqing Jiaotong University(Natural Science),2016,35(4): 93-99.