基于遗传K均值算法的军事装备试验数据分组模型

马晨光，刘庆国，李亚雄

(火箭军工程大学， 西安 710025)

装备试验与评价是按照规定的程序、条件和方法获取装备的特性数据，并通过数据处理分析，考核验证装备的特性是否满足要求的活动[1]。随着信息化进程的不断深入，现代战争对于军事装备维修保养的要求也不断提高[2]。现有的军事装备维修保养引入了一些高科技手段，但如何在军事装备数量繁多，标准要求高的军事装备维修保养中，科学合理地安排维修保养计划仍是各级指挥员的当务之急。

K均值算法是一种无监督的聚类分析方法，但其分组数目需要事先指定，容易陷入局部最优，不具有客观性，而采用具有全局搜索能力的遗传算法则能够实现分组数目的自动学习。本研究以军事装备为研究对象，建立了基于遗传K均值算法的聚类分组模型，将不同的军事装备划分到不同的组。基于此，指挥员可以按照不同组别指定不同的维修保养计划，使得军事装备的维修保养更加科学化，更有利于长期战斗力生成。

1 相似性度量

相似性度量是进行聚类分组的依据，本文将不同军事装备试验数据进行归一化处理，采用欧氏距离作为相似性度量。在此之前需要进行数据清理、数据集成、数据装换和数据消减的数据预处理，详见文献[3]。由于各项军事装备试验数据采取的分制不同，需归一化后才能进行聚类分组。假设m=[ma,mb,…,mNN]和n=[na,nb,…,nNN]为两个军事装备，其中NN为军事装备试验数据项目的总数。归一化处理公式为

(1)

其中amax和amin为军事装备试验数据a项的最大最小值，在归一化处理后，采用加权系数的欧式距离作为相似性度量

(2)

其中ωkk为权系数。

2 K均值算法

K均值算法是一种使用最广泛的聚类算法[4-5]。算法以K为参数，把军事装备分为K个簇，使组内具有较高的相似度，而组间相似度较低。算法首先随机选择K个军事装备，每个军事装备初始代表了一个簇的平均值或中心，对剩余的每个军事装备根据其与各个簇中心的距离，将它赋给最近的簇，然后重新计算每个簇的平均值，不断重复该过程，直到准则函数收敛。准则函数为

(3)

式中：p表示军事装备试验数据；Ci表示第i个分组；mi表示组Ci的聚类中心。

K均值算法的描述如下：

1) 任意选择K个军事装备的试验数据作为初始的聚类中心。

2) 计算每个军事装备的试验数据与K个聚类中心的距离，并将距离聚类中心最近的其他军事装备试验数据划分到一组。

3) 计算每个组的质心(聚集点的均值)并重新计算每个军事装备的试验数据到质心的距离，并根据最小距离重新对相应的对象进行划分。重复该步骤，直到式1)不再明显发生变化。

3 基于遗传K均值算法的聚类分组模型

由于K均值算法对初始聚类中心比较敏感，容易陷入局部最优，加入具有全局搜索能力的遗传算法[6-7]则能够有效地解决该问题。

1) 染色体编码

本研究采用实数编码方式进行编码。图1中G1，G2，…，Gk为初始聚类中心点。

G1G2…Gk

图1 编码示意图

2) 初始种群的生成

为了获得全局最优解，初始种群完全随机生成。先将每个样本随机指派为某一类作为最初的聚类划分，并计算各类的聚类中心作为初始个体的染色体编码，共生成K个初始种群个体，由此产生第一代种群。

3) 适应度函数计算

本文的适应度函数计算式为

(4)

其中：a和b为正的常系数；E为准则函数，描述分组的紧密性；Gb描述的是组间的离散性，式(4)的含义为组间距离越大，组内距离越小，适应度函数值越大

(5)

式(5)中ci,cj分别为第i,j个聚类中心。

4) 遗传算子

选择：采用适应度比例法，根据各个体的适应度计算个体被选中的概率，用轮盘赌方法进行个体的选择。

交叉：本研究采用单点交叉：在两条需要交叉的染色体上，随机选取交叉点，然后交换交叉点右侧的基因，得到两个新的染色体。

变异：其具体操作过程是：对于每个变异点，从对应基因位的取值范围内取一随机数代替原有基因值。

结合K均值算法和遗传算法，得到遗传K均值算法流程(见图2)：

① 设置参数，包括初始分组数目K，种群的规模Mt，遗传终止代数hf，交叉概率Pc和变异概率Pm；

② 随机产生初始种群；

③ 以种群个体为聚类中心，采用K均值算法进行聚类分组，计算个体的适应度值；

④ 按照上文的遗传算子设计方法，得到新的后代；

⑤ 反复执行③到④，直到算法收敛或达到遗传终止代数，将得到适度值最优的个体作为结果。

4 实验结果及分析

本文以假设的200台某型军事装备的训练数据作为研究对象，数据结构包含：编号(S1-S400)，机动能力(A,100分制)、抗干扰能力(B,100分制)，打击能力(C,20分制)、打击精度(D,20分制)、运载能力(E,20分制)和生存能力(F,20分制)等各项军事装备试验数据(见表1)。设定初始K值为3，终止迭代次数为60，Pc和Pm分别为0.7和0.1。本文设置A,B,F 3个项目的权重为0.25,0.25,0.2，其他3项分别为0.1。

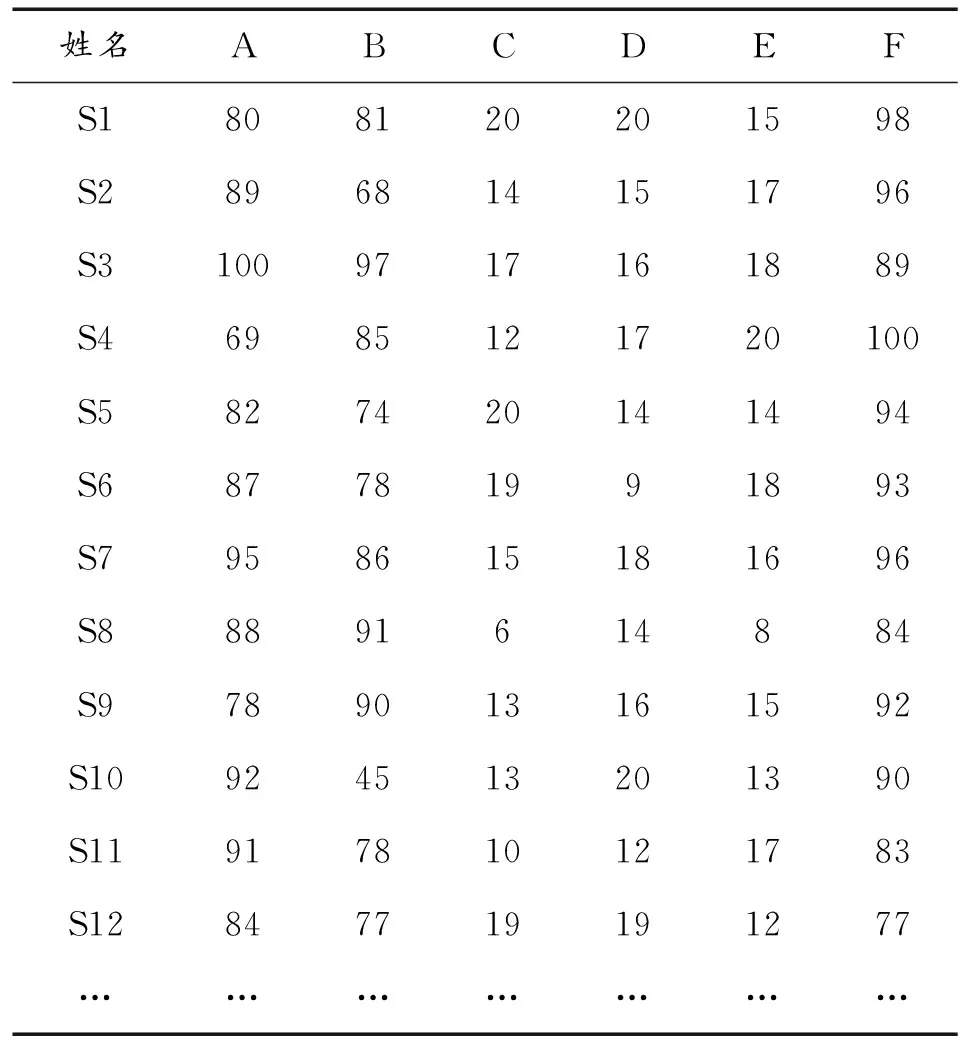
姓名ABCDEFS1808120201598S2896814151796S31009717161889S46985121720100S5827420141494S687781991893S7958615181696S88891614884S9789013161592S10924513201390S11917810121783S12847719191277…………………

经计算后，得到分组结果如表2所示。分组数目由最初的3变为5，实现了自动学习，说明遗传算法在K均值聚类分组中发挥了作用。第1、2、3、4、5组军事装备的数量分别为48，24，70，28和30，为指挥员按照组别制定维修保养计划打下了基础。

表2 分组结果

5 结论

本文给出了军事装备试验数据的相似性度量，采用遗传K均值算法对军事装备的试验训练数据进行了聚类分组，实验结果证明该方法实现了分组数目的自动学习，为指挥员按照组别指定维修保养计划打下了基础。

聚类分组仍有一部分内容需要进一步讨论和研究，如：聚类分组的有效性评价，依据分组结果制定科学合理的维修保养计划等。

参考文献：

[1] 廖兴禾，白洪波，丁建琪.基于系统工程的装备试验与评价需求研究[J].装备学院学报，2017，28(1)：118-123.

[2] 王志航.RFID技术在军事装备维修保养中的应用[D].济南:山东大学，2008.

[3] 李健平.决策树技术在军事训练成绩中的分析研究[D].昆明:昆明理工大学，2010.

[4] 邓敏，刘启亮，李光强，等.空间聚类分析及应用[M].北京：科学出版社，2011.

[5] 吕可,郑威,赵严冰.雷达对抗侦察装备作战能力的ANP幂指数评估方法[J].火力与指挥控制,2016(12)：59-63.

[6] 赖玉霞，刘建平，杨国兴.基于遗传算法的K均值聚类分析[J].计算机工程，2008，34(20)：200-202.

[7] 王玉斌.数据挖掘技术在辅助决策中的应用研究[D].重庆:重庆大学，2008.