集装箱船舶关键位置的摇摆概率模型

王培良， 吴晓芳, 张 婷

(1. 上海海事大学，航运仿真技术教育部工程研究中心，上海 201306; 2. 潍坊科技学院 汽车工程学院，山东 潍坊 262700; 3. 交通运输部水运科学研究院，北京 100089；4. 山东交通职业学院 航海学院，山东 潍坊 262700)

集装箱船舶关键位置的摇摆概率模型

王培良1,2， 吴晓芳3, 张 婷4

(1. 上海海事大学，航运仿真技术教育部工程研究中心，上海 201306; 2. 潍坊科技学院 汽车工程学院，山东 潍坊 262700; 3. 交通运输部水运科学研究院，北京 100089；4. 山东交通职业学院 航海学院，山东 潍坊 262700)

为揭示船舶航行安全与船舶摇摆(尤其是横摇)之间的内在关系，针对集装箱船舶关键位置在船舶正常航行过程中产生的摇摆构建摇摆概率模型，讨论和确定与之相关的参数。研究结果表明，集装箱船舶不同位置的摇摆角度及加速度的概率模型均主要服从高斯分布，但其相关参数不同。该方法从集装箱船舶摇摆的角度为船舶结构安全和航行安全研究提供一定的理论依据。

集装箱船舶；船舶摇摆；高斯分布；航行安全

为满足世界航运贸易发展的需求，集装箱船舶正朝着高速化、大型化和多用途方向发展，随之产生的船舶安全性问题备受关注。由船舶摇摆(尤其是横摇)引发的船舶倾覆事件时有发生，造成的生命和财产损失巨大。[1]因此，对船舶安全航行中关键位置(如艏部、舯部等)的摇摆进行建模，并求解关键位置在平衡状态下的摇摆概率模型，对于检测船舶航行的安全性和预测船舶横摇而言是十分必要的。

1 理论与方法

将船舶在航行过程中某关键位置处的摇摆记为随机变量V，包括纵摇角度、横摇角度和垂直加速度等3个维度，分别记为VZ，VH和VA。VZ，VH和VA在船舶航行过程中的采样值分别记为集合Z={xz1,…,xzi,…,xzn}，H={xh1,…,xhi,…,xhn}，A={xa1,…,xai,…,xan}，其中采样点个数为n。

1.1 高斯分布

高斯分布也称为正态分布，自然界中有很多随机现象都服从该分布。相关研究[2-3]证明，海浪波面起伏、船舶摇摆角度和波浪中船体的弯曲应力等都服从高斯分布。因此，假定集装箱船舶正常航行过程中不同位置处的摇摆(包括纵摇角度、横摇角度及垂直加速度)变化值能被描述成高斯分布，且所服从分布的参数是不同的。[4]

设随机变量X的密度函数为

(1)

式(1)中：μ和σ为常数(待估)，且σ>0。称X为服从参数μ和σ的正太分布，或高斯分布，记为X～N(μ,σ2)，其相应的分布函数为

(2)

1.2 模型验证

首先假定船舶航行过程中的摇摆变化值符合高斯分布或威布尔分布，为验证假定的可接受程度，需对样本观测数据进行总体分布的粗略推断。采用直方图技术和q-q图技术对其进行验证：首选采用q-q图技术对船舶2个数据观测点进行验证，判定其是否服从相同的分布，若服从相同的分布，则后续采用直方图技术绘制其中一组样本数据即可初步判定服从哪类分布，否则需分别判定2个观测点的分布特征。

q-q图是样本分位数与指定分布的分位数的关系曲线图，可用q-q图技术来检验样本数据是否服从指定的分布。利用MATLAB统计工具箱中的qqplot函数既可绘制1个样本的q-q图，检验样本是否服从指定分布，还可绘制2个样本的q-q图，检验2个样本是否服从相同的分布。[5]

在非参数统计领域，直方图技术可在密度估计及数据分析方面发挥重要作用，能对总体分布进行初步粗略估计，为研究总体的概率密度提供重要依据。[6]本文采用MATLAB自带的hist函数对观测点样本值进行纵向、横向和垂向的数据统计处理，获取各方向角度及加速度大小变化的概率密度函数的初步估计。[7]

1.3 模型参数的估计与模型检验

初步确定概率密度函数之后，需对其参数进行确定，本文采用最大似然估计法确定高斯分布或威布尔分布的位置参数。该方法的理论基础是实际推断原理——概率最大的事件最可能发生。

设总体X的密度函数为f(x;θ)，其中θ=(θ1,θ2,…,θk)，且(X1,X2,…,Xn)为总体X的一个样本，则样本的联合密度函数为

(3)

若一次抽取得到的样本观察值为(y1,y2,…,yn)，则样本(X1,X2,…,Xn)在观察值(y1,y2,…,yn)邻域内的概率为θ的似然函数可表示为

(4)

式(4)中：L(θ)为θ的函数。因此，要找到一个θ*使L(θ)达到最大，以此作为未知数θ的一个估计，该方法称为最大似然估计法。通常利用导数求极限法来求L(θ)的最大点，本文可采用该方法求得式(1)及式(2)中μ和σ在较高置信度下的最大似然估计，从而确定概率模型中的待估参数。

在确定模型参数之后，还需对船舶摇摆概率模型进行检验，主要校验样本值与假定的概率模型之间的匹配程度。本文采用MATLAB自带工具箱中的normplot和wblplot实现，若样本值符合假定的概率模型，则样本值与某条概率密度曲线是线性重合的。[8]

1.4 算法描述

船舶摇摆概率模型估计算法可描述为：

1)选定船舶结构中某2处位置为摇摆测试点，记录这2个点在船舶航行过程中各方向上的摇摆变化值，分别记为

Z={xz1,…,xzi,…,xzn}

(5)

H={xh1,…,xhi,…,xhn}

(6)

A={xa1,…,xai,…,xan}

(7)

2)采用直方图技术和q-q图分布对式(5)～式(7)进行统计，获取随机变量Z，H和A各自符合概率密度分布类型的初步估计。

3)对步骤2)推断的概率模型进行检验，确保所推断的模型与理想模型之间的误差在可接受范围之内。

4)基于步骤3)验证所得的假定概率模型，采用最大似然估计法对概率密度分布模型中的参数进行计算，最终确定具体的概率分布模型。

5)执行以上步骤之后即可获取航行中集装箱船舶某2个摇摆位置处摇摆变化值的概率模型。

2 试验数据获取及结果

2.1 试验数据获取

研究数据来自于上海海事大学万吨级远洋教学实习船“育锋”轮。该船的具体参数见表1。

为测定船舶的摇摆值，在艏部位置V1及舯部位置V2处安置角度传感器(见图1)。[9]

“育锋”轮在正常航行过程中，其角度传感器采集V1及V2处的纵向摇摆角度、横向摇摆角度和垂向加速度，共持续3 h。在该时间段内，传感器按照时间序列共触发47次，每次触发之后每个传感器可连续采集并返回100个角度和加速度的样本值。因此，每个测试点均有4 700个随机采样值，图2和图3分别为每次触发时的角度及加速度大小的平均值序列。[8]

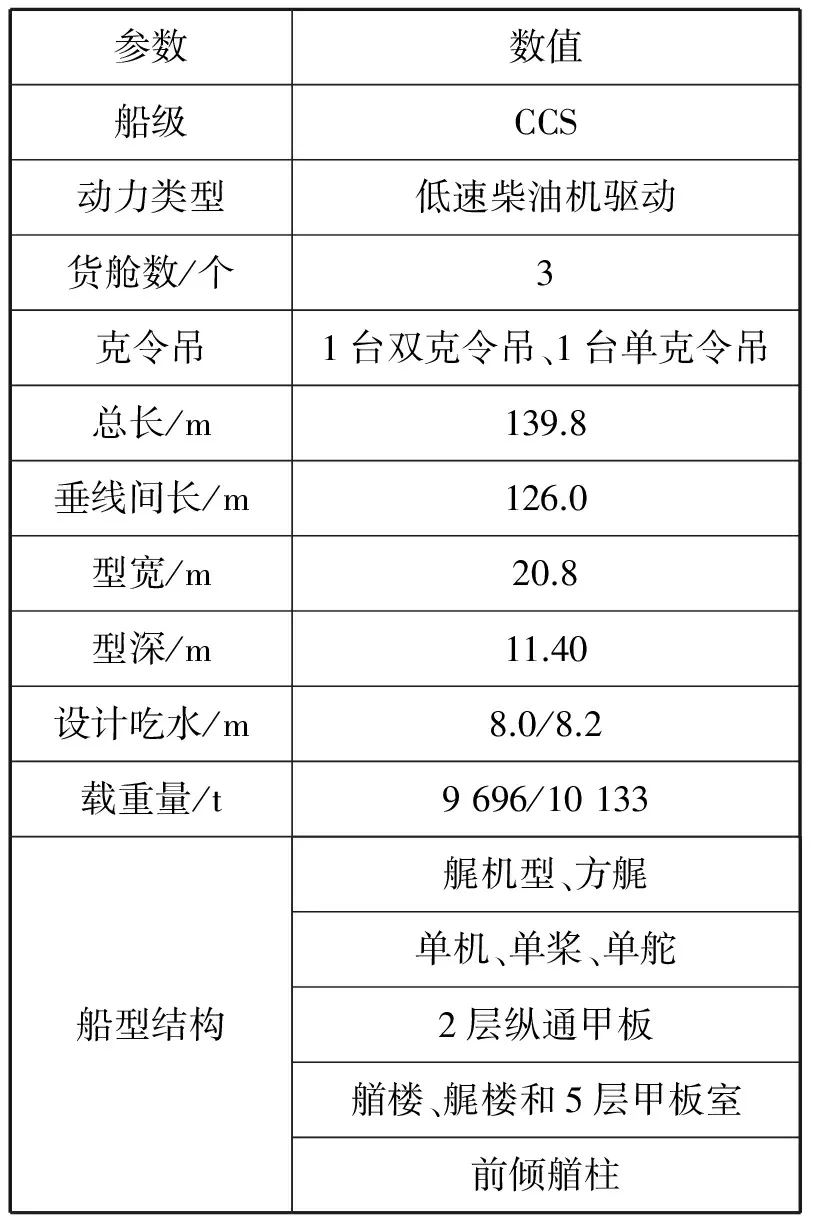
表1 “育锋”轮具体参数

图1 “育锋”轮传感器测点布置

2.2 试验结果及分析

2.2.1分布一致性判定

首先使用q-q图判定V1和V2各方向上的变化值是否符合相同分布，结果见图4。

由图4可初步推断V1和V2处纵向角度变化值、横向角度变化值及垂直方向加速度变化值均服从相同分布。后续只对V1处进行概率模型判定，V2省略。

2.2.2概率模型判定

利用直方图技术对“育锋”轮上2处传感器采集的各方向上的摇摆角度及加速度变化值进行初步统计分析和概率验证，结果见图5～图7。

a)纵向摇摆角度均值

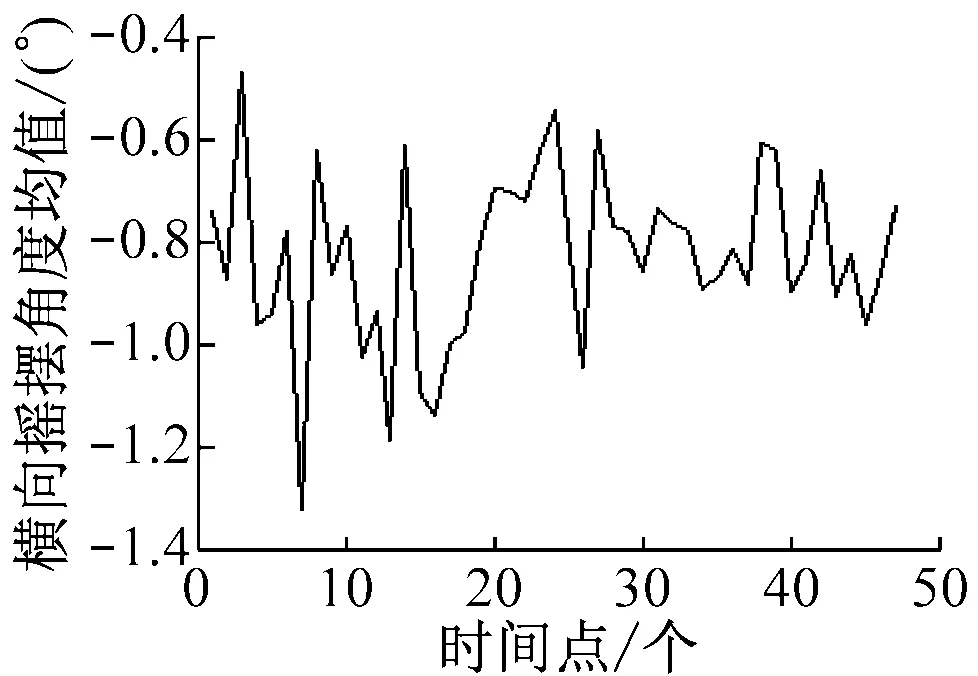
b)横向摇摆角度均值

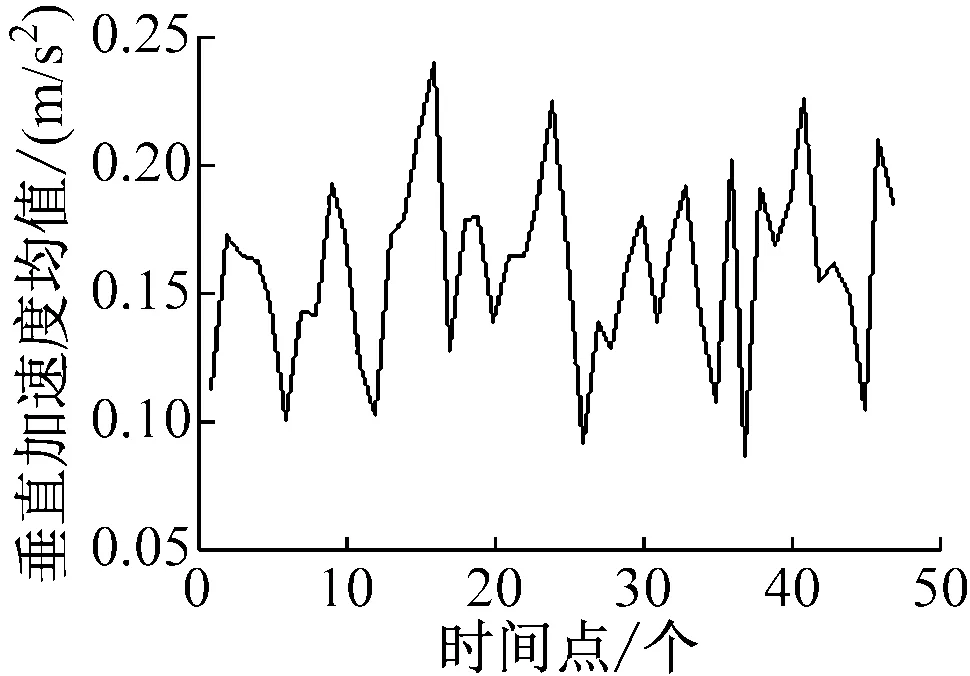
c)垂向加速度均值

图2V1点在传感器依此触发时的角度及加速度变化值的平均序列

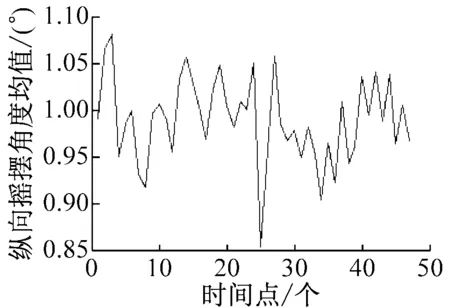
a)纵向摇摆角度均值

b)横向摇摆角度均值

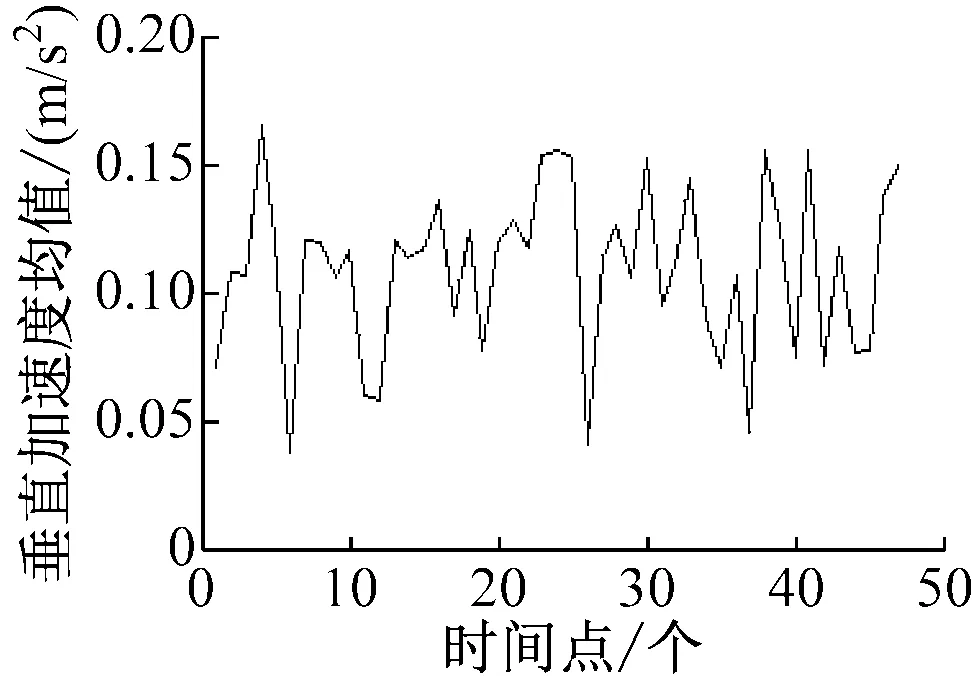
c)垂向加速度均值

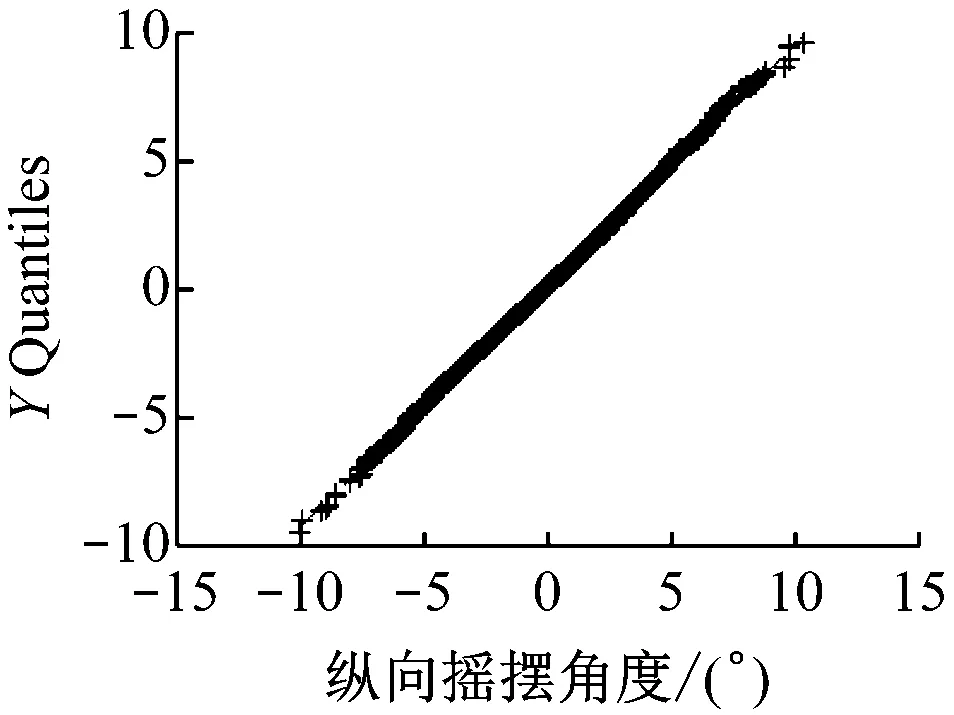
a)纵向摇摆角度均值

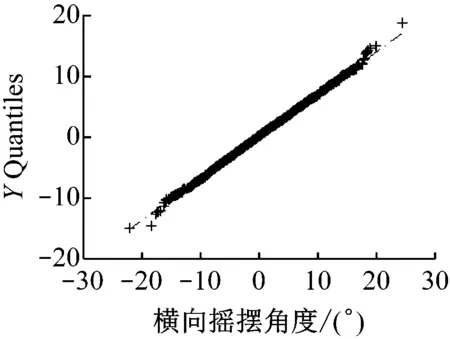
b)横向摇摆角度均值

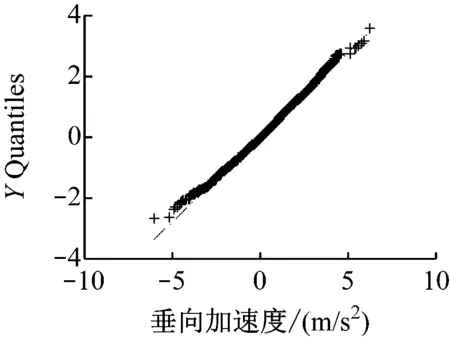
c)垂向加速度均值

图4V1及V2各方向对应的q-q图

a)纵摇角度变化频率分布

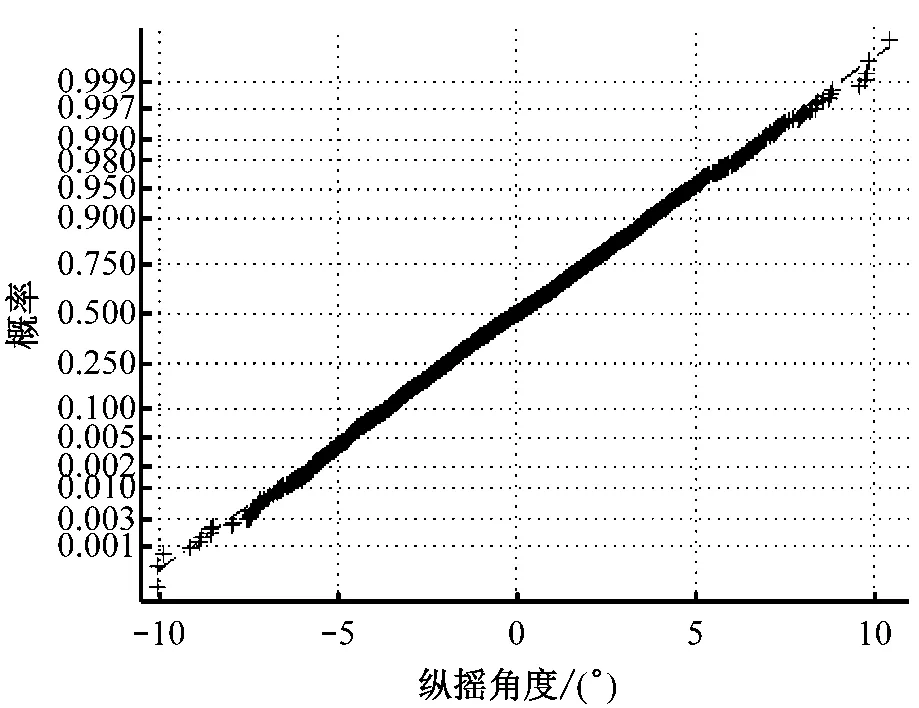
b)纵摇角度变化正太分布概率验证图

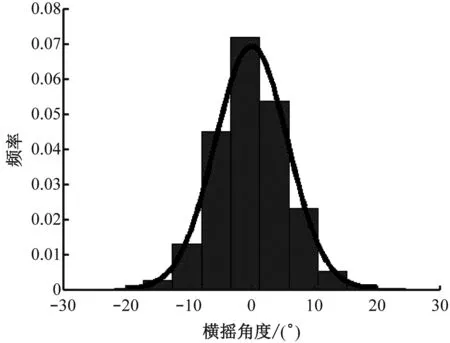
a)横摇角度变化频率分布

b)横摇角度变化正太分布概率验证图

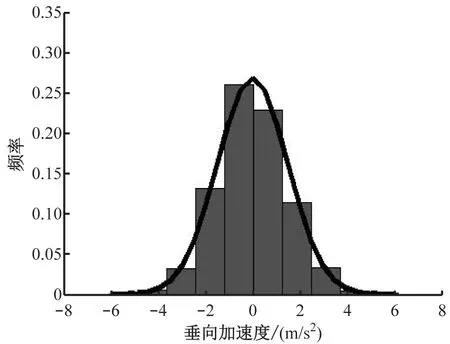
a)垂向加速度变化频率分布

b)V1垂向加速度正太分布概率验证图

由图5可知，其纵摇变化值近似服从高斯分布。利用normplot函数进行验证，结果显示‘+’号均在参考线附近，说明样本观测数据近似服从正太分布，与直方图初步估计的结果一致，同时图6和图7中均有相同的结果。因此，该处的摇摆角度变化值及加速度变化值近似服从高斯分布是可信的。

2.2.3模型参数估计及分析

根据上述校验的各方向上的摇摆角度概率模型结果，采用最大似然估计法确定相应的高斯模型的参数(主要是总体均值和方差)，具体见表2。

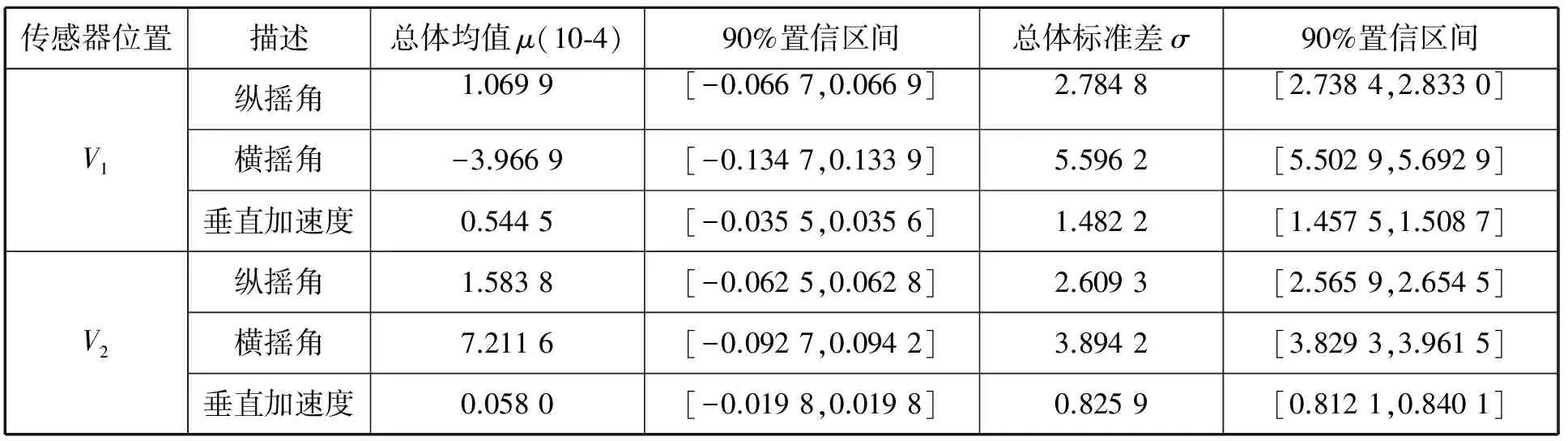
表2 摇摆角度及加速度概率模型参数

由表2可知：测量位置V1及V2处的纵向摇摆角度变化值趋向相同；横向摇摆角度变化值相差较大，说明船舶在航行过程中受横风、横浪影响较大(与“育锋”轮航行过程监控视频所得结果一致)；垂向的加速度变化值V1处较V2处波动大，与实际航行过程中艏部垂向变化幅度比舯部位置大相一致。

3 结束语

探索一种新型集装箱船舶安全航行过程中不同位置处的摇摆变化概率模型，该模型包括纵向及横向的角度变化概率模型和垂向的加速度变化概率模型。研究发现，集装箱船舶在安全航行过程中，其关键位置处的摇摆角度及加速度模型均服从不同参数的高斯分布。该研究从集装箱船舶摇摆的角度及加速度2方面为船舶结构安全和航行安全研究提供了一定的理论依据。

[1] 高儒. 集装箱船综合安全评估(FSA)研究[D]. 大连：大连海事大学, 2013.

[2] 万培峰. 砰击和波浪诱导响应的组合方法及考虑维修的船体可靠性分析[D]. 武汉：武汉理工大学, 2001.

[3] 孙德建, 胡雄, 金永兴,等. 集装箱船舶结构状态的在线监测技术研究[C]// “工程与振动”科技论坛， 2009.

[4] 金永兴, 张世斌. 集装箱船体波浪载荷应力短期分布的统计分析[J]. 上海交通大学学报, 2012(8):1243-1247.

[5] 赵嶷飞, 王晨, 王红勇. 基于ADS-B的航迹误差分布规律研究[J]. 中国民航大学学报, 2012, 30(6):48-52.

[6] CHEN X R, ZHAO L C. Almost Sure L 1-Norm Convergence for Data-Based Histogram Density Estimates[J]. Journal of Multivariate Analysis, 1987, 21(1):179-188.

[7] 肖筱南. 新编概率论与数理统计[M]. 北京：北京大学出版社, 2013.

[8] 金永兴, 胡雄, 施朝健. 集装箱船舶结构状态监测与评估系统[J]. 上海海事大学学报, 2008, 29(3):1-4.

[9] 金永兴, 伍生春. 船舶结构与设备[M]. 北京：人民交通出版社, 2012.

[10] 王倪传,石玉虎,覃闻铭.船舶结构不同应力点的应力概率模型[J]. 上海海事大学学报,2015,36(4):62-67.

ProbabilisticModelforSwayingatKeyPositionsonContainerShip

WANGPeiliang1,2,WUXiaofang3，ZHANGTing4

(1. Engineering Research Center of Simulation Technology of Ministry of Education, Shanghai Maritime University, Shanghai 201306, China; 2. Mechanical Engineering Department, Weifang University of Science and Technology, Weifang 262700, China; 3. China Waterborne Transport Research Institute, Beijing 100089, China; 4. Marine Academy, Shandong Transport Vocational College, Weifang 262700, China)

To reveal the inherent relationship between the operation safety of the ship and the swaying of the ship, especially the rolling, a probabilistic model for swaying at the key positions on container ships in normal navigation is constructed. The corresponding parameters of the probabilistic model are studied and defined. It is concluded that the probabilistic model regarding ship swaying follows Gaussian distribution, but the parameters can vary widely, dependent on ship design. The proposed method is of value for the study of structure safety and navigation safety of container ships at sea.

container ship; ship swaying; Gaussian distribution; navigation safety

2017-10-25

上海市科学技术委员会项目(14170501600)；山东省教育科学研究课题(16SB057)

王培良(1987—)，男，山东潍坊人，博士生，研究方向为载运工具运用工程。E-mail：gfy5216@126.com

1000-4653(2018)01-0070-04

U661.32+1

A