加测陀螺边的井下导线控制网抗差总体最小二乘算法

司亚君，何燕兰

(江苏省地质测绘院，江苏 南京 211102)

1 引 言

由于受作业环境的限制，导线测量仍然是井下平面控制测量的主要作业方法，其成果精度的高低是影响井上、井下测量基准一致性的重要因素。突发灾害发生时，井上、下测量基准的统一对确定事故发生地点、救生通道的顺利打通有重要意义。同时，导线测量成果也是矿区“一张图”建设、数字矿山建设的基础数据[1，2]。为获得较高精度的矿区测量数据，在应用现代测量手段、提高测量仪器的硬件性能，以获取更高精度的矿山测量外业数据的同时，研究人员一直在探讨与改进矿山测量数据处理的数学模型与方法[3～5]。数学模型的有效性与适用性是测量数据处理精度的关键，传统加测陀螺边的井下导线控制网的数据处理方法是在最小二乘准则(least squares，LS)的基础上，建立高斯-马尔可夫模型(Gauss-Markov model，G-M model)求解参数[6]。当观测向量含有的误差满足正态随机分布时，最小二乘估计为最优、无偏估计。受仪器观测精度、矿区作业环境的限制以及数据处理模型线性化等因素的影响，使得观测向量中含有误差的同时，模型的系数矩阵中也含有误差，并且可能含有粗差；此时，应用最小二乘估计求解参数不再具有最优、无偏的特征[7]。因此，在最小二乘准则基础上进行井下导线网平差计算的传统方法具有一定的缺陷。

为解决导线网数据处理模型的观测向量与系数矩阵中同时含有误差的问题，将总体最小二乘准则(total least squares，TLS)引入导线网测量数据处理。总体最小二乘是由Adcock为解决变量中含有误差(error-in-variables，EIV)的问题于1877年提出[8]；1980年，Golub和Van Loan提出可行性较强的基于奇异值分解算法[9](singular value decomposition，SVD)，总体最小二乘准则在图像处理、信号处理、化学工程等专业开始有广泛应用[10～12]；2008年，Burkhard Schaffrin和Andreas Wieser提出适合处理加权条件下的基于拉格郎日函数的总体最小二乘算法[13]，总体最小二乘受到测绘工作者更多的关注与研究[14～16]。

在建立加测陀螺边井下导线控制网间接平差模型的基础上，为实现对观测向量与系数矩阵中含有的误差同时进行最小化的约束，基于拉格郎日函数，给出模型参数的总体最小二乘迭代算法。为克服观测向量与系数矩阵中含有粗差对模型参数求解的影响，应用Huber权函数[17]，对观测向量与系数矩阵的权矩阵进行迭代定权，降低含有粗差的观测值对参数求解的影响。应用某矿区两井定向的导线控制网数据对提出的算法进行验证，并与传统算法在精度上进行比较。

2 平差模型

设两相邻控制点的水平距离与方位角分别为Si、ai，两相邻控制点的平面坐标为(xiyi)、(xi+1yi+1)，则：

(1)

(2)

为应用线性估计模型求解参数，须将式(1)，式(2)分别线性化：

(3)

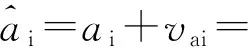
(4)

(5)

(6)

(7)

上诸式中，lsi、lβi、lai分别为边长观测值、角度观测值、陀螺边的方位角初值减去其观测值。

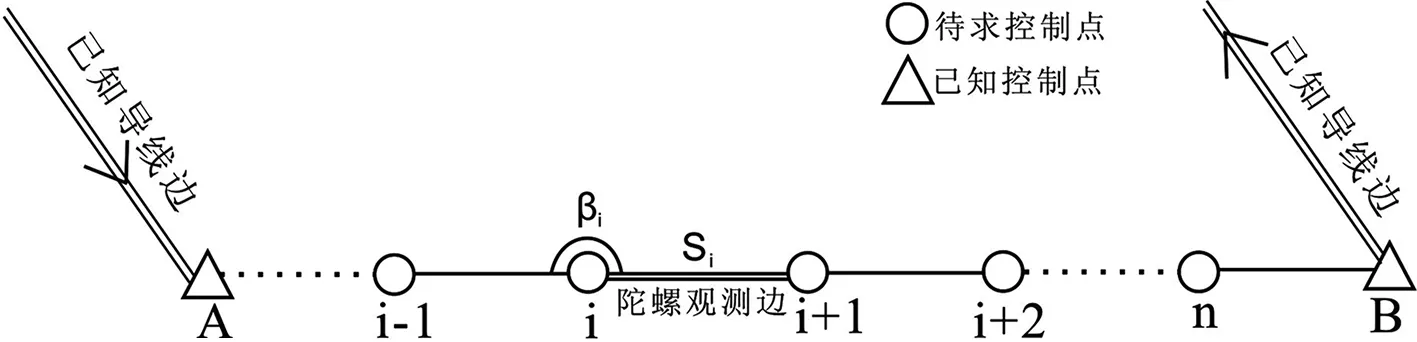
图1井下导线控制网

现有一井下导线控制网(如图1所示)，有n个待求控制点，共观测(n+1)条边的距离、(n+2)个水平角、加测t个陀螺边。以待求控制点平面坐标改正数为变量，建立间接平差模型：

(8)

应用最小二乘准则：

vTPv=min

(9)

(10)

式中P为观测向量的权矩阵，单位权方差与参数的协方差矩阵：

(11)

(12)

式(11)中，r为多余观测量。

应用最小二乘准则求解参数的前提是偶然误差仅存在于观测向量中。根据加测陀螺边的导线网平差模型(式(8))，模型的系数矩阵由观测元素的函数组成，同时，在对式(1)、式(2)进行线性化的过程中，也会引入舍入误差。因此，导线网模型的系数矩阵中也含有误差；此外，受井下观测环境与硬件性能等因素的限制，观测量中会混入粗差。此时，应用最小二乘准则进行井下导线网平差不再具有无偏、最优的性质。

3 模型参数的抗差总体最小二乘算法

为对观测向量与系数矩阵中含有的随机性误差同时实现最小化约束，克服系数矩阵与观测向量中含有粗差对参数求解的影响，基于迭代选权的思想，应用总体最小二乘准则求解变量中含有误差的井下导线网模型待估参数：

(13)

式中，P1为观测向量的权矩阵；b为系数矩阵B中含有的误差矩阵，P2为其权矩阵。并且：

(14)

式中，vec(b)表示对矩阵b进行列向量化；Q1、Q2分别为观测向量与系数矩阵的协因数阵。根据拉格郎日函数，建立如下模型：

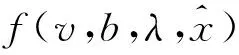
=min

(15)

式中，λ为拉格郎日乘数。要使式(15)最小，则函数对各变量的偏导数等于零，即：

(16)

(17)

(18)

(19)

根据式(16)～式(19)，建立模型参数的抗差迭代算法[16]。

(1)计算模型参数的初值

(20)

(2)根据参数的初值(式(20))，计算参数的总体最小二乘解

(21)

式中，Q0为m×m阶矩阵，Qb为n×n阶矩阵，同时Q0⊗Qb=Q2(⊗为矩阵的克罗内克积)。协因数阵Q1、Q2根据其权矩阵计算。应用式(16)、式(17)、式(22)计算v、b的初值，根据给定的限值判断观测向量与系数矩阵中是否含有粗差，并根据Huber权函数迭代定权[17]

(22)

(23)

令Pi=kPi-1，则观测向量与系数矩阵的协因数阵可以重新确定，并参与以下的迭代计算。需要指出的是，自适应调节因子矩阵k(式(22))也须参与以下的迭代计算。

(22)

(23)

(24)

算法的基本步骤为：①在最小二乘准则下求解参数的最小二乘解，并据此计算参数的总体最小二乘解的初值；②根据参数总体最小二乘解的初值以及由拉格郎日函数导出的相应条件，在Huber权函数的基础上，判断观测值中是否含有粗差，并重新计算模型的权阵及其协因数阵；③根据重新确定的协因数阵，迭代求解参数的估计直到收敛于给定的域值；需要注意的是，在迭代过程中，协因数阵应根据Huber权函数参与迭代计算，以不断降低含有粗差的观测值对参数求解的影响。

4 算例与分析

应用某矿的井下导线控制测量数据，对论文提出的算法进行验证。仪器的水平角观测精度为4″，陀螺经纬仪的定向精度为10″，激光测距离仪的测距精度为 2 mm+2 ppm×D。导线网如图2所示。

图2 某矿井导线控制网

已知控制点A的平面坐标为(xA=50.789 m，yA=8 057.566 m)，控制点B的平面坐标为(xB=7.81 m，yB=8 108.035 m)，角度观测值、已归算为平面距离的距离观测值、加测的陀螺边方位角观测值如表1所示。

井下导线控制网观测数据 表1

分别应用最小二乘准则与总体最小二乘准则求解待估控制点的坐标，控制点的坐标与求解精度(点位中误差σD)如表2所示。

不同准则求解的控制点坐标及其精度 表2

为应用抗差总体最小二乘算法对加测陀螺边的井下导线网进行平差，将部分观测数据中加入粗差，分析含有粗差的观测值对不同算法的扰动性影响。混入粗差的观测值如表3所示。

混入粗差的观测值 表3

分别应用最小二乘估计(LS)、稳健估计[16](rubust estimation，RLS)、总体最小二乘估计[13](TLS)、以及本文的抗差总体最小二乘估计(RTLS)对混入粗差的观测值与其他观测值组成的导线网进行平差，点位中误差与单位权中误差如表4所示。

不同算法求解的精度 表4

表4的计算结果表明，含有粗差的观测值对导线网平差有显著影响。由于最小二乘算法与总体最小二乘算法不具有抗差性，精度呈现一定的衰减。相比较而言，基于稳健估计的最小二乘算法与总体最小二乘算法统计精度较高；由于能够同时对观测向量与系数矩阵中含有的误差实现最小化的约束，本文的抗差总体最小二乘算法求解精度高于稳健最小二乘算法，适用于井下加测陀螺边的导线网平差。

5 结 论

在对加测陀螺边的井下导线控制网建立间接平差模型的基础上，对由于受观测环境与仪器观测精度的限制，导致数据处理模型的观测向量与系数矩阵中都会含有误差，指出应用最小二乘准则处理井下导线控制网数据只是对观测向量中存在的误差进行最小化约束。为克服传统数据处理方法存在的不足，实现对模型的观测向量与系数矩阵中含有的误差进行最小化的约束，同时顾及粗差对模型参数的影响，在应用拉格郎日函数的基础上，建立了基于Huber权函数的总体最小二乘抗差迭代算法。结合某矿的两井定向数据，验证算法在进行加测陀螺边的井下导线网平差的有效性，并从点位中误差与单位权中误差两个角度与其他算法进行了比较。结果表明，本文算法优于其他算法，更适用于井下导线控制网的测量数据处理。

[1] 吴立新，殷作如，邓智毅等. 论21世纪的矿山——数字矿山[J]. 煤炭学报，2000，25(4)：337～342.

[2] 吴立新，殷作如，钟亚平. 再论数字矿山：特征、框架与关键技术[J]. 煤炭学报，2003，28(1)：1～6.

[3] 亢瑞红，郭广礼，胡洪. Helmert定权在井下平面控制导线网平差中的应用[J]. 金属矿山，2010(11)：104～107.

[4] Guo Jinyun，Guo Shuyang，Liu Xin. On Zero Position Correction of Hanging Tape of Gyro-theodelite[J]. Survey Review，2008，40：129～134.

[5] Wetherelt A，Hunt P. Azimuth Determinations using an Adapted wild GAKI(an Alternative Approach)[J]. Survey Review，2004，37：592～603.

[6] 张国良，朱家钰，顾和和. 矿山测量学[M]. 徐州：中国矿业大学出版社，2001.

[7] 崔希璋，於宗俦，陶本藻等. 广义测量平差[M]. 武汉：武汉大学出版社，2001.

[8] Adcock R J. Note on the method of least squares [J]. Analyst，1877，4：183～184.

[9] Golub G H，Van Loan C F. An Analysis of the Total Least Squares Problem[J]. SIAM J Number，Anal，1980，17：883～893.

[10] 杨鸿森．基于总体最小二乘的红外图像去噪[J]. 激光与红外，2008，38(9)：961～964.

[11] Van Huffel S，Vandewalle J. Analysis and Solution of the Nongeneric Total Least Squares Problem[J]. Siam Jourmal on Matrix Analysis & Applictions，1988，9(3)：360～372.

[12] Lemmerling P，De Moor B，van Huffel S. On the Equivalence of Constrained Total Least Squares and Structured Total Least Squares[J]. IEEE Transactions on Signal Processing，1996，44(11)：2908～2911.

[13] Burkhard Schaffrin，Andreas Wieser. On Weighted total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy，2008，82：415～421.

[14] Zhang S L，Tong X H，Zhang K L，et al. A Solution to EIV Model with Inequality Constraints and its Geodetic Applications[J]. Journal of Geodesy，2013，87：89～99.

[15] Mahboub V. On Weighted Total Least-squares for Geodetic Transformations[J]. Journal of Geodesy，2012，86：359～367.

[16] 陶叶青，高井祥，姚一飞. 基于中位数法的抗差总体最小二乘估计[J]. 测绘学报，2016，45(3)：297～301.

[17] 周江文，黄幼才，杨元喜等. 抗差最小二乘法[M]. 武汉：华中理工大学出版社，1997.