南海神狐海域天然气水合物降压开采过程中储层的稳定性

万义钊 吴能友 胡高伟 辛 欣 金光荣 刘昌岭 陈 强

1.青岛海洋地质研究所国土资源部天然气水合物重点实验室2.青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室3.吉林大学环境与资源学院 4.中国科学院广州能源研究所

0 引言

天然气水合物（以下简称水合物）广泛存在于海底的沉积物和陆地多年冻土带中，分布范围广、资源量巨大、能量密度高，有望成为满足未来人类能源需求的高效清洁能源[1]。目前，水合物开采的方法主要有降压法、注热法、注化学试剂法和二氧化碳置换法等。国际上已经有少数国家[2-6]开展了水合物试采，使用降压法开采海洋水合物的国家如日本、中国[6]，其中产量最高的是我国于2017年5月10实施的海域水合物试采，累积产气量为30.9×104m3，平均日产气量为5 151 m3[6]，本次试采稳定产气60 d。

总结上述国际天然气水合物历次试采经历可知，总体上水合物的开采效率仍然较低；降压法是最行之有效的方法。水合物降压开采通过降低井底压力在储层中形成压降漏斗，当储层压力降低到水合物相平衡压力以下时，水合物开始分解。理论上，井底压力降低幅度越大，压降漏斗影响范围越大，产气速率就越大[7]，但储层压力降低会导致储层有效应力增大和垂向变形，同时由于海洋天然气水合物储层胶结差，强度低，储层应力增大可能引起储层失稳破坏，而水合物又在储层沉积物颗粒间起胶结作用，降压引起的水合物分解会降低储层的强度，进一步加大了储层失稳的风险。因此，储层稳定性是水合物开采面临的关键问题，是确保水合物开采安全高效的前提。

据最新勘探结果显示，我国南海北部神狐海域水合物储层以黏土质粉砂和粉砂质黏土为主，储层沉积物粒径总体低于20 μm，是典型的孔隙充填型水合物储层[8-9]，储层原位测试渗透率低（＜10 mD）。许多学者利用数值模拟的手段研究神狐海域水合物的开采方法和开采潜力。Zhang等[10-11]建立了神狐海域水合物降压+注热开采方法的单一水平井和双水平井模型，对其产气能力进行了评价。李刚等[12-14]利用注热结合降压以及热吞吐等方法对神狐海域水合物开采潜力进行了研究，讨论了不同井型的开采效果。苏正等[15]也对神狐海域直井热激发的开发方法进行了评价。这些数值模拟研究对神狐海域水合物的直井、水平井、双水平井等开采井型进行了详细分析，对降压、注热、热吞吐等开采方式进行了模拟。

国内外的学者对水合物开采的储层变形和破坏也开展了初步的研究。沈海超等[16]将水合物分解效应融合到渗流场与岩土变形场中，建立水合物开采的流固耦合数学模型，对降压开采过程中近井地带的储层稳定性进行了数值模拟。程家望等[17]将储层沉降和井壁稳定性结合到降压开采过程中，建立了一维的水合物降压开采稳定性数学模型，模型不考虑传热过程的影响。孙可明等[18]建立了反映水合物分解引起储层力学性质劣化的热流固耦合模型，利用ABAQUS二次开发了模型的求解程序，研究了加热法开采水合物储层变形破坏规律。

然而，目前针对神狐海域黏土质粉砂和粉砂质黏土水合物储层开采过程中的力学稳定性问题研究很少[19]。本文基于南海神狐海域水合物的钻探资料，建立三维的水合物降压开采的地质模型，综合考虑储层中水合物的分解、传热、渗流和骨架固体变形的多场耦合过程，建立水合物开采储层稳定性分析的数学模型及有限元求解方法，获取水合物降压开采过程中储层压力、温度、饱和度和应力的时空演化特征，分析神狐海域水合物降压开采过程中储层沉降、应力分布和稳定性。

1 物理模型

2015年9月，中国地质调查局在我国南海北部陆坡神狐海域完成第3次海域天然气水合物钻探航次（GMGS3）。本次钻探的GMGS3-W19站位水深为1 273.9 m，确定海底以下135～170 m范围内存在厚度约为35 m的水合物层。根据钻探资料，建立了如图1所示的物理模型。水平方向上，模型以井为中心向x方向和y方向延伸400 m。模型的顶面为海底面；水合物赋存于135 m以下，厚度35 m；水合物层上部是135 m的上覆层，底部为厚94 m的下伏层，均不含水合物。打开井段为135～162 m，即打开水合物储层顶部向下的28 m[20]。

图1 GMGS3-W19站位模型示意图

2 数学模型及求解

2.1 基本假设

水合物开采是一个复杂的传热传质过程，包括多相流体在多孔介质中的渗流、热对流和热传导、水合物分解的化学反应以及含水合物沉积物的固体变形。为建立描述水合物开采物理过程的数学模型，需做如下假设：①假设水合物为纯I型的水合物，水合物中气体为100%甲烷，且忽略冰的生成；②在选取的控制体内，保持局部热力平衡，即沉积物固体颗粒和流体（气体、液体）的温度相同；③气和水在多孔介质中的流动符合Darcy定律；④水合物属于孔隙充填型，附着在沉积物颗粒表面，且水合物和沉积物颗粒组成连续的复合固体材料，共同受力，其土力学特性为线弹性。

2.2 数学模型

基于以上假设建立综合考虑热场、气水两相渗流场、沉积物固体变形场和水合物分解的化学场的热—流—固—化（THMC）的四场耦合模型。

2.2.1 水合物分解动力学的化学场

水合物分解的质量守恒方程：

基于Kim-Bishoni的动力学模型[21]，水合物分解时的产气速率为：

相应地，水合物分解的产水速率和水合物消耗速率为：

2.2.2 气水两相渗流场

水合物沉积物中气和水在多孔介质中的流动可用连续方程和Darcy定律表示，最终得到气水两相渗流的模型方程。

气相：

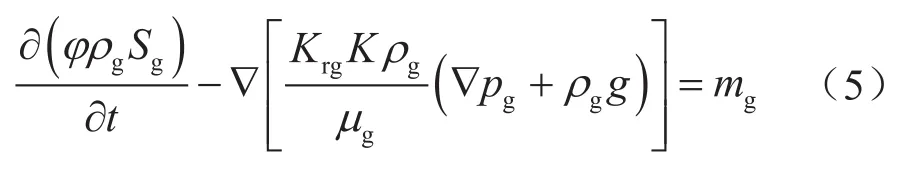
水相：

方程（5）、（6）右端项中的mg、mw由水合物分解动力学模型计算，这两项是耦合渗流场与化学场的关键。

2.2.3 热场

水合物分解过程中的热场可以由能量守恒方程来表示。考虑储层的热传导和热对流的水合物分解时能量守恒方程为：

其中

2.2.4 含水合物沉积物固体变形力场

水合物—沉积物复合固体变形的平衡微分方程为：

根据Terzaghi有效应力原理，土体的总应力等于水合物和沉积物颗粒骨架组成的复合固体的有效应力与孔隙压力之和[22]，则有：

其中

根据线弹性假设，复合固体的应力应变关系为：

其中

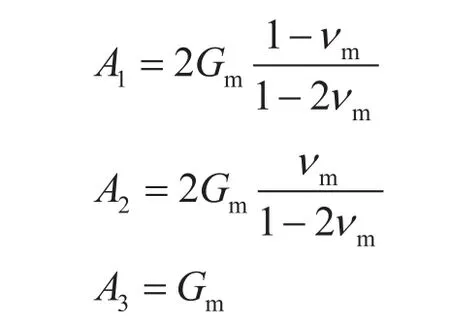
2.2.5 辅助方程

除各物理场的控制方程外，还需各物理参数的辅助方程，主要有：

2.2.5.1 绝对渗透率方程[23]

2.2.5.2 毛细管力和气水两相相对渗透率方程[24]

其中

2.2.5.3 水合物相平衡压力方程[25]

2.2.5.4 水合物相变潜热方程[26]

2.2.5.5 水合物—沉积物颗粒复合固体力学性质方程

三轴实验结果表明：水合物的存在会增大含水合物沉积物的强度，但水合物对泊松比的影响很小[27]，因此，假设泊松比为常数，弹性模量Em由Santamarina和Ruppel[28]提出的公式来表示：

以上方程构成了水合物开采过程的四场耦合模型。

2.3 有限元求解

经过分析，THMC的四场耦合模型可以分为两个子系统：包含传热传质的流动系统和固体变形系统。用有限元方法分别对两个子系统求解。

对流动系统，选取pg、Sw、Sh、T作为独立的求解变量。其中Sh可以利用方程（1）和方程（4）直接求得，现推导pg、Sw、T有限元方程。

2.3.1 pg的有限元方程

将方程（5）的第一项展开有：

利用气体状态方程：

将方程（5）中的密度替换为压力，可得气相压力方程为：

对上式乘以δpg并积分，并用高斯公式降阶可得：

将压力在单元上用插值函数表示：

代入可得最终气相压力的有限元求解方程：

其中

2.3.2 Sw的有限元方程

利用毛细管力方程可得：

将方程（6）中水相压力用气相压力和水相饱和度表示，则有：

上式乘以δpw并积分，降阶并利用高斯公式有：

将饱和度在单元上用插值函数表示：

代入可得最终饱和度的有限元求解方程：

其中

2.3.3 T的有限元方程

方程（7）乘以δT并积分可得：

其中

第二个子系统是固体变形模型，其控制方程是式（14）。以x方向为例，对x方向的平衡微分方程乘以δux并积分，降阶可得：

由插值函数可得：

可得x方向的有限元方程为：

其中

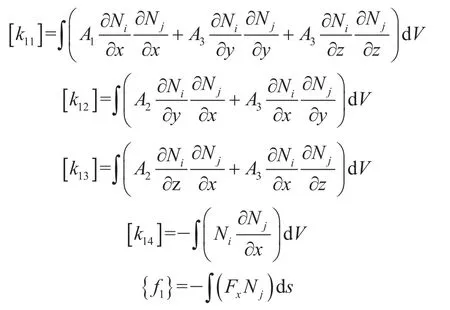
同理可得y方向和z方向的有限元单元方程。

2.4 模型网格划分

采用四面体非结构网格对图1所示的物理模型进行网格划分，其网格图如图2所示。为提高计算精度，在水合物层中加密网格，网格总数为38 068。

2.5 初始条件和边界条件

图2 神狐海域水合物开采模型网格图

根据GMGS3-W19站位的调查结果，海底面的温度为3.75 ℃，地温梯度为0.045 ℃/m，按储层深度折算，储层初始温度在纵向上线性分布。地层初始时刻的孔隙压力随深度逐渐增加，符合静水压力平衡。水合物层的水合物初始饱和度为0.45，上覆层和下伏层全部为水，水饱和度为1。井底的压力保持定压力生产，储层的外边界为保持原始地层压力的定压边界条件。

初始的地应力分布可由饱和土土体自重折算。模型顶面的水深为1 273.9 m，折算顶部压力为12.86 MPa，沉积物密度为2 650 kg/m3，则地层应力以25.97 kPa/m的梯度纵向递增。固体变形场的边界条件为：上顶面为自由面边界；储层下底面为纵向固定条件；侧面为水平位移固定条件，即垂直于x=0 m，x=800 m的侧面，沿x方向的位移为0；垂直于y=0 m和y=800 m侧面，沿y方向的位移为0。

2.6 物性参数

模型水深为1 273.9 m，上覆层厚度为135 m，下伏层厚度为94 m，井底生产压力为5.0 MPa，水合物层底界初始压力14.3 MPa，水合物层底界初始温度为14.0 ℃，其热物性、渗透率等参数如表1所示。

含水合物沉积物力学性质参数如表2所示。

3 模型验证

为验证数值模型及程序的正确性，将模型计算结果与Masuda实验结果进行对比。Masuda采用Berea砂岩合成水合物进行降压开采实验的模型如图3所示。

Berea岩心长30 cm，直径5.1 cm，放置于温度为2.3 ℃的恒温空气浴中。岩心的初始温度（Ti）为2.3 ℃，初始孔隙压力（pgi）为3.75 MPa，初始水合物饱和度（Shi）为0.443，水饱和度（Swi）为0.351，孔隙度（φi）为0.182，渗透率（Ki）为98 mD。实验过程中，A端作为出口保持2.84 MPa的恒定压力。实验记录出口的累计产气量。

表1 南海神狐海域W19站位水合物储层物性参数表

表2 南海神狐海域含水合物沉积物力学参数表

图3 Berea岩心实验模型示意图

利用本文建立的有限元计算程序计算上述算例，获得出口端的累计产气量随时间的变化。与实验结果进行对比。累计产气量对比结果如图4所示。从对比结果看，笔者建立的多场耦合模型可以与实验结果较好地吻合，证明了模型和算法的有效性和可靠性。

图4 本文计算的累计产气量与实验结果对比图

4 结果分析及讨论

4.1 产水产气特征

图5是井底压力定为5 MPa条件下产水和产气速率随时间变化曲线。由图5可知，井底压力降低后，井附近的地层压力随之降低，这导致井附近水合物分解，试采井产水产气速率开始保持一个较高值，之后迅速降低。待产水速率上升时，产气速率逐渐增加；由于压力传导的速度较快，产水速率能很快到达相对稳定的状态；产气速率也到达相对稳定的波动状态。

4.2 物理场分布特征

在本模型均质假设条件下，预测得到开采60 d时的压力变化、水合物饱和度、温度变化、气体饱和度等在空间上的变化特征（图6）。

由图6-a可知，井压力降低区域主要集中在试采井附近，生产井中心的压力最低，压力比初始地层压力降低约9 MPa；其水平方向上的影响范围大致为井附近35 m内，即压降从井中心的9 MPa到0 MPa的范围为35 m；在5 MPa生产压力下，水合物饱和度分解区被限制在生产井附近，在水平方向上，水合物的分解区大约离井2 m范围内。因储层渗透率较低，储层底部的水合物还未完全分解，起到了一定的阻水作用。

由图6-c可知，开采60 d时，水合物分解的吸热效应并不能造成温度在空间上明显的变化，井中心的温度最大降低约－4 ℃；沿水平方向，温度的降低范围较小，这印证了水合物分解范围较小的事实。水合物分解产生的甲烷气体一部分运移到生产井产出，一部分积聚在孔隙空间中，由于气体饱和度的增加，在两相渗流的毛细管力作用下，气体不能完全产出，形成了如图6-d的气体饱和度分布。

4.3 力学响应特征分析

在储层选取两个点，监测其孔隙压力、温度和应力随时间的变化情况。近井处和远井处的坐标分别为（x=0.3 m，z=149 m）和（x=8.1 m，z=149 m）。

图5 GMGS3-W19站位产气产水随时间变化曲线图

图6 试采60 d后井周物理场变化图（负值表示比初始值低）

图7 z为149 m处的近井处和远井处的力学响应变化曲线图

从图7-a可知，由于井底降压，近井处的孔隙压力迅速降低后达到稳定值。远井处孔隙压力表现为平缓下降趋势，近井处孔隙压力低于远井处。近井处的孔隙压力降低导致水合物分解，水合物分解吸热导致其温度降低（图7-b）；当水合物分解完毕后，由于周围传热原因，温度逐渐回升。对于远井处，其孔隙压力降低不足以使得水合物大量分解，故其温度基本保持不变。

由图7-c可知，孔隙压力降低引起有效主应力增加。近井处的有效应力因该处孔隙压力的快速降低而较快地升高，最后保持不变（由于是定井底压力开采）。远井处的孔隙压力降低幅度较小，其有效主应力增加较为缓慢。降压使得近井处的最大与最小主应力之差比远井处的大，故近井处剪应力增加较远井处的明显。

图7-d是两个点的最大和最小有效主应力随开采时间的变化情况，即有效应力路径，由图7-d可知，在t=0时刻，两点的应力状态处于沉积物的摩尔—库伦抗剪强度线[30]的破坏线之外，即表示该处在沉积历史中已经处于压缩稳定的状态。当开采后，其应力路径均表现为近井处0～1 d内的变化较快，1 d后变化缓慢；远井处的应力变化滞后于近井处。因两点的应力路径均表现为偏离摩尔—库伦强度线，其没有靠近或达到破坏线上，表示没有发生破坏。故基于本模型的初步预测结果显示，开采60 d内储层不会发生破坏。

4.4 储层沉降分析

图8显示了开采过程中垂向位移的情况，即生产降压导致海底沉积物发生的沉降。由图8-a、c知，生产井降压造成空间上的沉降形如漏斗；从俯视角度（xOy平面）看，沉降以井位置处为中心呈圆形分布，井位置处的沉降最大。从切面图（图8-b、d）可知，在生产井段处的沉降较小，而在生产井段上下的垂向位移变化最大。故生产井段上方附近的沉降量最大，而生产井段下方在渗透压的作用下发生局部隆起。生产井段上方的土体在上覆应力作用下，其沉降量大于生产井段下方的隆起量。由于生产井段上方的土体在应力作用下整体发生沉降，生产井降压造成的沉降影响范围大于孔隙压力影响范围。

图8 开采井段（135～162 m）引起沉降空间分布状态图

图8 中在30 d时，井位置处的最大沉降量为0.032 m（即32 mm）；而海底面沉降约为0.014 m，海底面沉降范围（＞5 mm）的半径约为166 m；随开采进行，60 d时生产井位置的最大沉降量为0.035 m，海底面沉降约为0.018 m，海底面沉降范围（＞5 mm）的半径约为232 m。沉降量和沉降范围均随生产进行逐渐增大。

图9-a是生产井位置海底面的沉降量（垂向位移）随时间的变化情况。在前15 d，沉降约0.009 m（即9 mm）。随后，因孔隙压力在空间上逐渐趋于动态平衡状态，海底面处的沉降速率降低。60 d后沉降逐渐变得缓慢，最终达到的0.018 m。可见前15 d的沉降占到总沉降量的1/2，故定压开采条件下，其沉降主要发生在开采前期。

图9-b是生产井位置处不同时刻的沉降量(垂向位移)情况，由图9-b可知，由于降压导致的应力变化主要集中在生产井周围，故降压点附近发生较大位移；又因降压点下方底部是固定不动的，不发生垂向位移，降压点底部的隆起部分将因边界效应使得其隆起量为0。模型顶部是自由面，可以自由移动，海底面以下一定深度范围内的沉积物是整体下沉。

4.5 渗透率对储层沉降的影响

渗透率是影响气水运移和压力影响范围的关键因素。图10是不同渗透率下，生产井位置处海底面的沉降随时间变化关系图。

由图10可以看出，渗透率较低时，压降范围较小，海底面沉降的下降速率基本保持不变；而当渗透率增加时，压降范围增加，沉降先以较高的速率发生，之后沉降速率降低，最后海底面以较低的沉降速率发生沉降。对于渗透率分别为1.0 mD、2.5 mD和5.0 mD，以60 d时的沉降量为基准，其沉降一半所需要的时间分别为24 d、15 d和9.5 d。随渗透率增加，沉降速率加快，达到相同沉降量的时间提前。

4.6 井底压力对储层沉降的影响

井底压力大小直接地影响地层中孔隙压力分布范围，引起骨架有效应力的变化，进而影响储层的沉降。图11是不同生产压力下，生产井位置处海底面的沉降在生产过程随时间的变化规律。从图11可以看出，在生产前期，不同生产压力下的沉降基本一致，差异较小；待进入稳定产气速率阶段后，海底面的沉降逐渐产生差异。在60 d时，其沉降量分别为0.016 m、0.018 m和0.020 m；其沉降一半所需时间约为15 d。生产压力降低，沉降速率增加，达到相同沉降量所需时间提前，但其影响程度比渗透率的影响程度小。

图9 生产井位置的海底面沉降量随时间和储层深度的变化图

图10 生产井位置的海底面沉降随渗透率变化图

图11 生产井位置的海底面沉降随生产压力变化图

5 结论

1）以南海北部神狐海域的天然气水合物钻探资料为基础，建立了水合物单一垂直井降压开采的物理模型，利用非结构网格对模型进行划分；考虑水合物开采过程中的传热传质和沉积物变形过程，建立了热—流—固—化的四场耦合模型，基于非结构网格，采用有限元方法对模型进行求解，获得储层的孔隙压力、温度、饱和度和应力的时空演化特征。

2）神狐海域水合物储层渗透率较低，降压开采时压力降低的影响范围有限，主要局限在井筒附近范围内，水合物的分解范围也较小。

3）水合物开采过程中，储层中孔隙压力的减小导致了有效应力的增加，有效应力的增加主要在井筒附近，且井筒附近的最大和最小主应力之差比远井处的大，故近井地带的剪应力较大，易发生剪切破坏。开采60 d井筒附近应力路径线远离摩尔—库伦的强度包线，这表明在本模型的假设条件下，储层不会发生破坏。

4）有效应力增大导致储层的沉降，开采60 d，储层最大沉降为32 mm，海底面最大沉降为14 mm，且储层沉降主要发生在开采的早期。

5）储层渗透率和降压开采的井底压力对储层沉降影响明显。储层渗透率越大、井底压力降压幅度越大，储层沉降量越大，且沉降的速度越快。

致谢：感谢日本东京大学Shigemi Naganawa博士提供的Masuda实验数据。

符 号 说 明

t表示时间，s；pw、pg分别表示水相、气相压力，Pa；pc表示毛细管压力，Pa；pe表示水合物平衡压力，Pa；Sh、Sg、Sw分别表示水合物、气相、水相的饱和度；ρh、ρw、ρs、ρg分别表示水合物、水相、沉积物颗粒、气相的密度，kg/m3；ρm表示水合物和沉积物颗粒组成复合固体的密度，kreac表示水合物分解速率常数，mol/(m2·Pa·s)；Ars表示单位体积储层水合物分解的表面积，m－1；mw、mh、mg分别表示水合物分解产水速率、单位体积水合物分解速率、单位体积储层中水合物分解的产气速率，kg/(m3·s)；Nh表示水合物数；MCH4表示甲烷气体的摩尔质量，kg/mol；MH2O表示水相的摩尔质量，kg/mol；Mh表示水合物摩尔质量，kg/mol；Krg、Krw分别表示气水两相渗流的气相、水相的相对渗透率；K、K0分别表示沉积物多孔介质、不含水合物时的绝对渗透率，m2；Krgo、Krwo表示无水合物时的气相端点、油相端点的相对渗透率；n表示渗透率递减指数；ng、nw分别表示气相、水相相对渗透率指数；Sgr、Swr分别表示气相、水相相对渗透率端点的饱和度； μg、μw分别表示甲烷气体、水相黏度，Pa·s；φ表示含水合物沉积物孔隙度；g表示重力加速度，m/s2；T表示储层温度，K；Cw、Cg、Ch、Cs分别表示水相、气相、水合物相、沉积物颗粒相的比热容，分别表示水相、气相相对于控制体的速度，m/s；λs、λg、λw、λh分别表示沉积物颗粒、甲烷气相、水相、水合物热传导系数，W/(m·K)；Qh表示水合物分解的相变潜热，W/m3；σ表示含水合物沉积物的总应力张量，MPa；σ'表示复合固体的有效应力，MPa；σc0表示参考围压，MPa；α表示Biot系数；ε表示应变张量；I表示单位向量； 表示表示沉积物固体变形位移，m；Gm、lm分别表示水合物和沉积物颗粒组成复合固体的拉梅常数；Em、Es0、Eh分别表示复合固体、不含水合物沉积物在参考围压σc0下、纯水合物的弹性模量，MPa；vm表示复合固体泊松比；b表示σc围压条件下，沉积物弹性模量的敏感系数；c表示水合物弹性模量系数；d表示水合物饱和度非线性效应系数；A0～A5，B1、B2表示常系数。

[ 1 ] Klauda JB & Sandler SI. Global distribution of methane hydrate in ocean sediment[J]. Energy & Fuels, 2016, 19(2): 459-470.

[ 2 ] Dubreuil-Boisclair C, Gloaguen E, Bellef l eur G & Marcotte D.Non-Gaussian gas hydrate grade simulation at the Mallik site,Mackenzie Delta, Canada[J]. Marine and Petroleum Geology,2012, 35(1): 20-27.

[ 3 ] Uddin M, Wright F, Dallimore S & Coombe D. Gas hydrate dissociations in Mallik hydrate bearing zones A, B, and C by depressurization: Eあect of salinity and hydration number in hydrate dissociation[J]. Journal of Natural Gas Science and Engineering,2014, 21: 40-63.

[ 4 ] Schoderbek D, Martin KL, Howard J, Silpngarmlert S & Hester K.North Slope hydrate fi eld trial: CO2/CH4exchange[C]//OTC Arctic Technology Conference, 3-5 December 2012, Houston, Texas,USA. DOI: http://dx.doi.org/10.4043/23725-MS.

[ 5 ] Yamamoto K, Terao Y, Fujii T, Terumichi I, Seki M, Matsuzawa M, et al. Operational overview of the fi rst oあshore production test of methane hydrates in the Eastern Nankai Trough[C]. Oあshore Technology Conference, 5-8 May, Texas, USA.

[ 6 ] 陈惠玲, 朱夏. 南海神狐海域天然气水合物试采60天关井[N].中国国土资源报, 2017-07-10(1).Chen Huiling & Zhu Xia. The trial production well of gas hydrate from Shenhu area, South China Sea, shut down on the 60thday of production[N]. China Land Resource Report, 2017-07-10(1).

[ 7 ] Kurihara M, Sato A, Ouchi H, Narita H, Masuda Y, Saeki T, et al.Prediction of gas productivity from eastern Nankai trough methane-hydrate reservoirs[J]. SPE Reservoir Evaluation & Engineering, 2009, 12(3): 477-499.

[ 8 ] 梁金强, 王宏斌, 苏新, 付少英, 王力峰, 郭依群, 等. 南海北部陆坡天然气水合物成藏条件及其控制因素[J]. 天然气工业,2014, 34(7): 128-135.Liang Jinqiang, Wang Hongbin, Su Xin, Fu Shaoying, Wang Lifeng, Guo Yiqun, et al. Natural gas hydrate formation conditions and the associated controlling factors in the northern slope of the South China Sea[J]. Natural Gas Industry, 2014, 34(7):128-135.

[ 9 ] 于兴河, 王建忠, 梁金强, 李顺利, 曾小明, 沙志彬, 等. 南海北部陆坡天然气水合物沉积成藏特征[J]. 石油学报, 2014,35(2): 253-264.Yu Xinghe, Wang Jianzhong, Liang Jinqiang, Li Shunli, Zeng Xiaoming, Sha Zhibin, et al. Depositional accumulation characteristics of gas hydrate in the northern continental slope of South China Sea[J]. Acta Petrolei Sinica, 2014, 35(2): 253-264.

[10] Zhang KN, Moridis GJ, Wu NY, Li XS & Reagan MT. Evaluation of alternative horizontal well designs for gas production from hydrate deposits in the Shenhu area, South China Sea[C]//International Oil and Gas Conference & Exhibition, 8-10 June 2010,Beijing, China. DOI: http://dx.doi.org/10.2118/131151-MS.

[11] 胡立堂, 张可霓, 高童. 南海神狐海域天然气水合物注热降压开采数值模拟研究[J]. 现代地质, 2011, 25(4): 675-681.Hu Litang, Zhang Keni & Gao Tong. Numerical studies of gas production from gas hydrate zone using heat injection and depressurization in Shenhu area, the South China Sea[J]. Geoscience,2011, 25(4): 675-681.

[12] 李刚, 李小森, Zhang Keni, Moridis GJ. 水平井开采南海神狐海域天然气水合物数值模拟[J]. 地球物理学报, 2011, 54(9):2325-2337.Li Gang, Li Xiaosen, Zhang KN & Moridis GJ. Numerical simulation of gas production from hydrate accumulations using a single horizontal well in Shenhu area, South China Sea[J]. Chinese Journal of Geophysics, 2011, 54(9): 2325-2337.

[13] 李刚, 李小森, 陈琦, 陈朝阳. 南海神狐海域天然气水合物开采数值模拟[J]. 化学学报, 2010, 68(11): 1083-1092.Li Gang, Li Xiaosen, Chen Qi & Chen Zhaoyang. Numerical simulation of gas production from gas hydrate zone in Shenhu area, South China Sea[J]. Acta Chimica Sinica, 2010, 68(11):1083-1092.

[14] Li G, Moridis GJ, Zhang KN & Li XS. Evaluation of gas production potential from marine gas hydrate deposits in Shenhu area of South China Sea[J]. Energy & Fuels, 2010, 24(11): 6018-6033.

[15] 苏正, 何勇, 吴能友. 南海北部神狐海域天然气水合物热激发开采潜力的数值模拟分析[J]. 热带海洋学报, 2012, 31(5): 74-82.Su Zheng, He Yong & Wu Nengyou. Numerical simulation on production potential of hydrate deposits by thermal stimulation[J]. Journal of Tropical Oceanography, 2012, 31(5): 74-82.

[16] 沈海超, 程远方, 胡晓庆. 天然气水合物藏降压开采近井储层稳定性数值模拟[J]. 石油钻探技术, 2012, 40(2): 76-81.Shen Haichao, Cheng Yuanfang & Hu Xiaoqing. Numerical simulation of near wellbore reservoir stability during gas hydrate production by depressurization[J]. Petroleum Drilling Techniques,2012, 40(2): 76-81.

[17] 程家望, 苏正, 吴能友. 天然气水合物降压开采储层稳定性模型分析[J]. 新能源进展, 2016, 4(1): 33-41.Cheng Jiawang, Su Zheng & Wu Nengyou. A geomechanical stability model analysis of hydrate reservoir for gas hydrate production by depressurization[J]. Advances in New and Renewable Energy, 2016, 4(1): 33-41.

[18] 孙可明, 王婷婷, 翟诚, 罗慧玉. 天然气水合物加热分解储层变形破坏规律研究[J]. 特种油气藏, 2017, 24(5): 91-96.Sun Keming, Wang Tingting, Zhai Cheng & Luo Huiyu. Patterns of reservoir deformation due to thermal decomposition of natural gas hydrates[J]. Special Oil & Gas Reservoirs, 2017, 24(5): 91-96.

[19] Sun JX, Zhang L, Ning FL, Lei HW, Liu TL, Hu GW, et al. Production potential and stability of hydrate-bearing sediments at the site GMGS3-W19 in the South China Sea: A preliminary feasibility study[J]. Marine and Petroleum Geology, 2017, 86: 447-473.

[20] Yang S, Zhang M, Liang J, Lu J, Zhang Z, Melanie H, et al. Preliminary results of China's third gas hydrate drilling expedition:A critical step from discovery to development in the South China Sea[J]. Fire in the Ice, 2015, 15(2): 1-5.

[21] Kim HC, Bishnoi PR, Heidemann RA & Rizvi SSH. Kinetics of methane hydrate decomposition[J]. Chemical Engineering Science, 1985, 42(7): 1645-1653.

[22] Biot MA & Willis DG. The elastic coeきcients of the theory of consolidation[J]. Journal of Applied Mechanics, 1957, 15(2):594-601.

[23] Masuda Y, Naganawa S & Ando S. Numerical calculation of gas production performance from reservoirs containing natural gas hydrates[J]. SPE Journal, 1997, 29(3): 201-210.

[24] Sun XF & Mohanty KK. Kinetic simulation of methane hydrate formation and dissociation in porous media[J]. Chemical Engineering Science, 2006, 61(11): 3476-3495.

[25] Duan ZH & Sun R. A model to predict phase equilibrium of CH4and CO2clathrate hydrate in aqueous electrolyte solutions[J].American Mineralogist, 2006, 91(8/9): 1346-1354.

[26] Esmaeilzadeh F, Zeighami ME & Fathi J. 1-D modeling of hydrate decomposition in porous media[C]//Proceedings of World Academy of Science: Engineering & Technology, 2013, 43: 648.

[27] Soga K, Lee SL, Ng MYA & Klar A. Characterisation and engineering properties of methane hydrate soils[C]//Proceedings of the 2ndInternational Workshop on Characterisation and Engineering Properties of Natural Soils, 29 November-1 December 2006,Singapore. London: CRC Press, 2006.

[28] Santamarina JC & Ruppel C. The impact of hydrate saturation on the mechanical, electrical, and thermal properties of hydrate-bearing sand, silts, and clay[C]//Proceedings of the 6thInternational Conference on Gas Hydrate, 6-10 July 2008, Vancouver, British Columbia, Canada.

[29] Clarke M & Bishnoi PR. Determination of the intrinsic rate of gas hydrate decomposition using particle size analysis[J]. Annals of the New York Academy of Sciences, 2000, 912: 556-563.

[30] Rutqvist J, Moridis GJ, Grover T, Silpngarmlert S, Collett TS& Holdich SA. Coupled multiphase fluid flow and wellbore stability analysis associated with gas production from oceanic hydrate-bearing sediments[J]. Journal of Petroleum Science &Engineering, 2012(92/93): 65-81.