紧急解脱隔水管回弹响应分析*
2018-05-04王腾王科
王 腾 王 科
(中国石油大学(华东)石油工程学院 山东青岛 266580)
钻井隔水管是连接海底井口与钻井平台的重要部件[1],当浮式钻井平台遭遇极端恶劣海况或动力定位失效时,为了保护平台设备和人员安全、减少对海洋环境的破坏、避免隔水管断裂、保护水下井口,在来不及回收隔水管的情况下需进行隔水管的紧急解脱作业[2]。隔水管紧急解脱是指底部隔水管总成(LMRP)与防喷器(BOP)解脱,此时储存在隔水管系统中的势能释放出来,隔水管向上回弹,有可能会导致隔水管向上撞击钻井平台;解脱之后,钻井液下泄,钻井液的摩擦效应会导致隔水管向下延伸一定距离,LMRP有可能会撞击BOP造成事故[3]。控制隔水管紧急解脱后的回弹是深水钻井面临的技术难题之一,因此建立隔水管回弹响应模型,分析不同情况下的隔水管回弹响应过程和关键影响因素,对于保证深水钻井隔水管系统的作业安全有重要意义。
张磊 等[4]利用ANSYS软件将平台运动以动边界形式施加于弹簧单元,分析了隔水管不同张拉力及解脱时刻的回弹响应。Li 等[5]提出了整体流体模型、计算流体模型等2种回弹后钻井液下泄力的计算方法。Lang等[6]介绍了隔水管回弹响应分析方法研究的最新进展,初步探讨了利用有限元软件进行隔水管回弹响应分析方法,指出在钻井船升沉运动的不同时刻进行紧急脱离隔水管回弹响应有很大不同。Arild Grønevik[7]利用SIMA/RIFLEX软件分析了隔水管回弹在500 m和1 500 m水深条件下的回弹响应,但没有将钻井平台与隔水管系统进行整体耦合响应分析。上述研究虽然从不同方面对隔水管回弹响应进行了一定分析研究,但均没有考虑钻井平台与隔水管系统的整体耦合响应。笔者基于整体流体模型得到隔水管解脱后钻井液下泄力的变化规律,并通过ANSYS/AQWA External Force Calculation程序将钻井液下泄力引入隔水管回弹模型中,结合上部钻井平台的响应进行钻井平台与隔水管系统的整体耦合响应分析,并以1 500 m深水钻井隔水管为例,考虑钻井平台响应、隔水管张拉力和钻井液下泄力等关键因素对紧急解脱隔水管回弹响应进行仿真分析,以期为深水钻井紧急解脱隔水管安全作业提供参考。
1 隔水管回弹响应分析模型
1.1 张紧器模型
本文以直接作用式张紧器为研究对象,该张紧器的工作原理[8]如图1所示。Yang[9]通过详细研究储能器、液压缸及活塞与活塞杆的工作机理提出了计算张拉力与活塞位置的关系式,即

(1)
式(1)中:T为张拉力,N;T0为预张力,N;ΔZ为活塞冲程,m;Z0为液缸中的有效长度,取20 m;γ为15 ℃条件下的绝热气体常数,取1.4[10]。
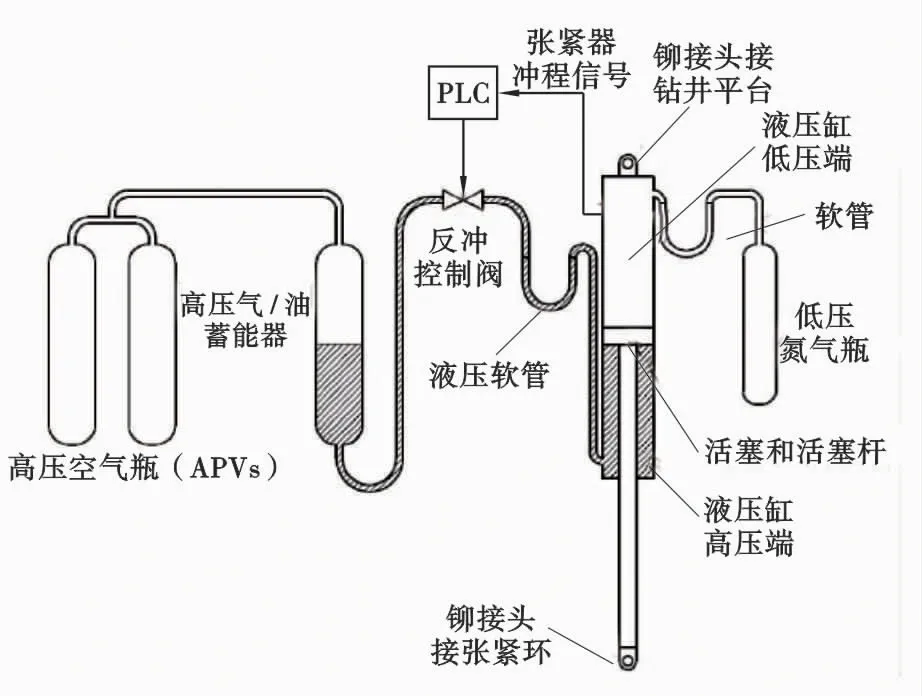
图1 直接作用式张紧器系统示意图[8]
为了在ANSYS/AQWA软件中用非线性模型模拟张拉力随冲程的变化规律,对式(1)在±10 m范围内的力位移变化曲线进行3次多项式拟合(图2),并以拟合式(2)为基础在AQWA软件中建立非线性张紧器模型。

图2 张拉力与冲程关系
3.45×10-4ΔZ3
(2)
1.2 钻井液下泄模型
当隔水管紧急解脱时,往往没有足够的时间来回收钻井液,而钻井液与海水之间的密度差会造成在隔水管的底部管内钻井液与管外海水之间的压差较大,因此当LMRP与BOP解脱之后,钻井液从隔水管内下泄进入海水,对隔水管的回弹产生重要影响[5]。基于整体分析方法用环空模型模拟钻井液,假设隔水管与钻柱之间的环空完全充满钻井液,将隔水管中的环形钻井液看作一个整体,当钻井液下泄进入海水时,海水立刻从隔水管上部的充填阀门循环进入隔水管环空。在时间t=0时LMRP与BOP实现解脱,钻井液自隔水管下泄进入海水中,经过一段时间管内外压差为零,系统处于平衡状态,环空模型如图3所示。
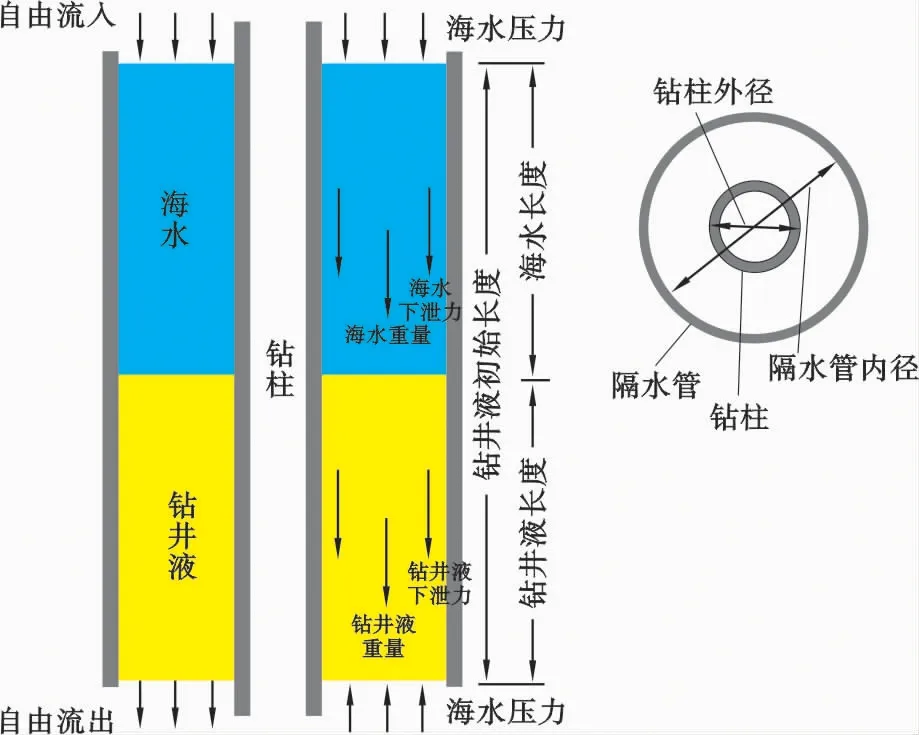
图3 隔水管环空模型示意图
由达西公式可知,回弹过程中的压力降可以表示为[7]
(3)
其中
Lz=L0-Ut
U=u0+at
D=d1-d2
由于钻井液在下泄过程中绝大多数时间内处于紊流流态,因此采用了紊流摩阻系数来计算管内流体的下泄力,摩擦力系数可从莫迪表[11]中得出,但考虑到流速的不断变化,摩擦力系数用Haaland公式计算[7],即
(4)
由钻井液下泄造成的水头损失可以表示为
(5)
进而得到钻井液的下泄力为
(6)
同理,取海水的摩擦力系数fw,参照式(6)可以得出管内海水对隔水管的下泄力为
-Lz)
(7)
结合式(6)、(7),在钻井液下泄的每一个时间步,在整体流体柱上运用牛顿第二定律建立整体流体模型(WFC)的控制方程,即
ρwgAe(L0-Lz)+ρmgAeLz-Fw-Fm-ρwgAeL0-

(8)
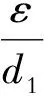
1.3 基于ANSYS/AQWA的钻井平台+张紧器+隔水管回弹模型
通过非线性多项式形式的弹簧模拟张紧器, ANSYS/AQWA External Force Calculation二次开发将下泄力施加在隔水管底部的LMRP上,用来模拟隔水管回弹后的钻井液下泄的影响,隔水管回弹耦合模型如图4所示。

图4 钻井平台与隔水管耦合系统示意图
2 隔水管回弹响应的敏感性分析
假设水深1 500 m,不规则波浪有效波高5 m、周期10 s,钻井平台、锚链、隔水管系统参数见表1~3。利用本文建立的紧急解脱隔水管耦合模型进行隔水管回弹响应的敏感性分析。

表1 钻井平台参数

表2 锚链参数

表3 隔水管系统配置[4]
2.1 钻井液下泄力影响分析
隔水管内径0.489 m、钻柱外径0.127 m,钻井液密度分别为1.28、1.60 g/cm3时钻井液下泄力随时间的变化关系如图5所示。由图5可以看出,钻井液密度越大,下泄力越大;钻井液下泄力在隔水管回弹开始后快速增大,之后缓慢减小。因此,钻井液密度较大条件下进行隔水管解脱作业时钻井液下泄力不可忽视。

图5 钻井液下泄力随时间变化曲线
当顶部张拉力为4.7 MN时,不同密度钻井液下泄力作用下LMRP的回弹响应曲线如图6所示。从图6可以看出,隔水管紧急解脱后,LMRP回弹至最高位置后进行垂向振动响应;钻井液密度越大,LMRP垂向振动振幅越大,当钻井液密度为1.60 g/cm3时LMRP在隔水管解脱6.1 s后下沉至水深1 491.93 m,距离BOP水深位置1 492 m仅0.07 m,易发生碰撞。
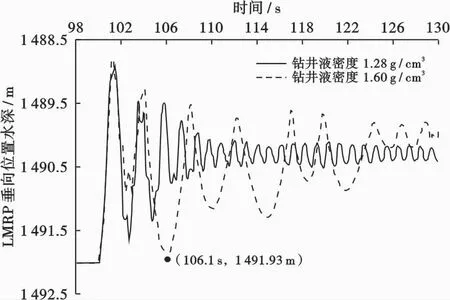
图6 钻井液下泄力对LMRP位置的影响
2.2 张拉力影响分析
顶部张拉力分别为4.7、5.7、6.7和7.7 MN时隔水管解脱后LMRP随时间变化曲线如图7所示。从图7可以看出,张拉力为4.7 MN时LMRP回弹最低水深位置为1 491.69 m,距离海底防喷器[13]仅0.31 m,易导致隔水管触底;张拉力为7.7 MN时LMRP回弹最高水深位置为1 487.85 m,易导致隔水管松弛。
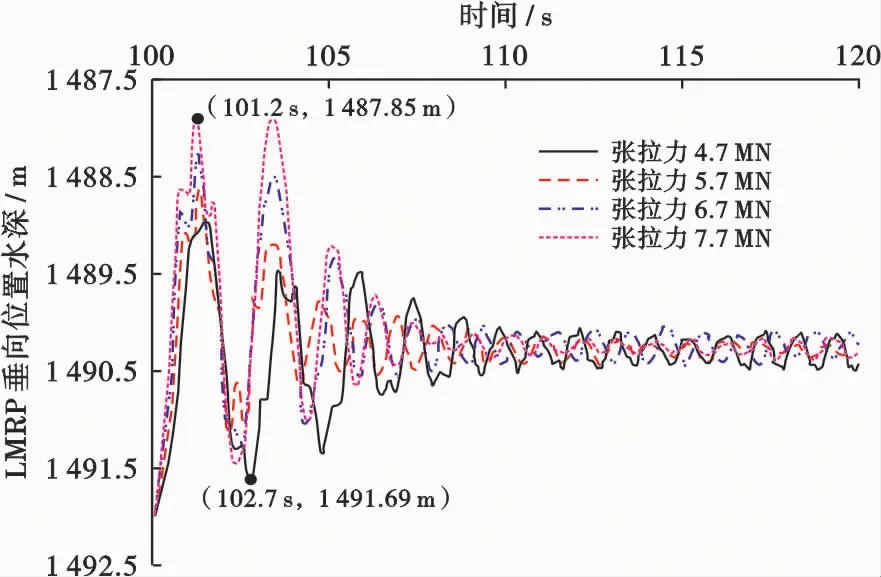
图7 不同张拉力时LMRP垂向响应
顶部张拉力分别为4.7、5.7、6.7和7.7 MN时隔水管解脱后伸缩节张力环位置随时间变化曲线如图8所示。从图8可以看出,张拉力越大,隔水管回弹导致的伸缩节冲程越大;隔水管解脱后0.29 s伸缩节开始响应,与应力波传递至1 500 m处的伸缩节所需要时间0.293 s相一致,同时不同张拉力情况下由隔水管重量控制的伸缩节逐渐稳定在9.5 m附近位置,二者间接证明了本文所建模型的准确性。通过张拉力对LMRP位移及伸缩节冲程的影响结果分析可知,隔水管的张拉力既不能过大使张紧器超出冲程,也不能过小使LMRP触底。因此,在现场作业中应根据钻井平台所处水深、钻井液密度、伸缩节冲程极限值计算安全的张拉力,以保证发生紧急解脱作业时钻井平台的安全。

图8 不同张拉力时伸缩节的垂向位置
3 结论
1) 综合考虑钻井液下泄力、张拉力等因素影响,利用ANSYS/AQWA建立了隔水管紧急解脱回弹耦合计算模型,该模型具有较好的计算准确性,可用来模拟分析隔水管解脱后的回弹响应。
2) 模拟计算结果表明:钻井液密度越大,钻井液下泄力越大,隔水管解脱后LMRP触底的可能性越大;张拉力对LMRP回弹位移和伸缩节的许用冲程影响较大,张拉力越大,LMRP回弹位移和伸缩节位移越大。因此,隔水管紧急解脱作业时应根据现场钻井平台的作业水深、海况条件、钻井液密度等条件选择合适的张拉力,既要防止张拉力过大导致伸缩节超出冲程撞击钻井平台,又要防止张拉力过小导致隔水管LMRP撞击防喷器。
[1] 畅元江,陈国明,许亮斌.海洋钻井隔水管固有频率的简化计算[J].中国海上油气,2005,17(5):352-355.
CHANG Yuanjiang,CHEN Guoming,XU Liangbin.Simplified calculation of natural frequencies for marine drilling risers[J].China Offshore Oil and Gas,2005,17(5):352-355.
[2] YOUNG R D,HOCK C J,KARLSEN G,et al.Analysis and design of anti-recoil system for emergency disconnect of a deepwater riser:case study[J].Emergency Equipment,1992.
[3] YANG C K,KIM M H.Transient effects of tendon disconnection of a TLP by hull-tendon-riser coupled dynamic analysis[J].Ocean Engineering,2010,37(8/9):667-677.
[4] 张磊,畅元江,刘秀全,等.深水钻井隔水管与防喷器紧急脱离后的反冲响应分析[J].石油钻探技术,2013,41(3):25-30.
ZHANG Lei,CHANG Yuanjiang,LIU Xiuquan,et al.Recoil analysis for deepwater drilling riser after emergency disconnection with blowout preventer[J].Petroleum Drilling Techniques,2013,41(3):25-30.
[5] LI C,FAN H,WANG Z,et al.Two methods for simulating mud discharge after emergency disconnection of a drilling riser[J].Journal of Natural Gas Science & Engineering,2015,28:142-152.
[6] LANG D W,REAL J,LANE M.Recent developments in drilling riser disconnect and recoil analysis for deepwater applications[C]∥ASME 2009,International Conference on Ocean,Offshore and Arctic Engineering,2009:305-318.
[7] GRØNEVIK A.Simulation of drilling riser disconnection-recoil analysis[J].Institutt for Marin Teknikk,2013.
[8] 李朝玮,樊洪海,汪志明,等.深水钻井隔水管紧急脱离后的反冲响应[J].海洋工程,2015,33(4):121-127.
LI Chaowei,FAN Honghai,WANG Zhiming,et al.Recoil response of deepwater drilling riser during emergency disconnection[J].The Ocean Engineering,2015,33(4):121-127.
[9] YANG C K.Numerical modeling of nonlinear coupling between lines/beams with multiple floating bodies[D].Texas:Texas A & M University,2009.
[10] LI S,CAMPBELL M,HOWELLS H,et al.Tension loss of hydro-pneumatic riser tensioners[C]∥ASME 2013,International Conference on Ocean,Offshore and Arctic Engineering,2013.
[11] 王弥康,林日亿,张毅.管内单相流体沿程摩阻系数分析[J].油气储运,1998,17(7):22-26.
WANG Mikang,LIN Riyi,ZHANG Yi.The analysis of pipe friction coefficient in single phase fluid[J].Oil Gas Storage and Transmission,1998,17(7):22-26.
[12] 刁宇,孙宝龙,王春生,等.高压压裂油套环空井压降计算[J].石油矿场机械,2014(3):26-29.
DIAO Yu,SUN Baolong,WANG Chunsheng,et al.The calculation of high pressure casing annulus' pressure drop[J].Oil Field Equipment,2014(3):26-29.
[13] 刘秀全,陈国明,畅元江,等.台风条件下深水钻井隔水管触底事故分析及对策[J].石油勘探与开发,2013,40(6):738-742.
LIU Xiuquan,CHEN Guoming,CHANG Yuanjiang,et al.Analyses and countermeasures of deepwater drilling riser grounding accidents under typhoon conditions[J].Petroleum Exploration and Development,2013,40(6):738-742.
