民间借贷机构利率能够精算定价吗?
——一个Black-Scholes模型的构建与检验
2018-05-04何涌
何涌
(1. 湖南工业大学 经济与贸易学院,湖南 株洲 412007;2. 中南大学商学院,长沙 410083)
一、引言
近年来,非法集资问题日益突出,e租宝、泛亚的大案要案频发。作为民间借贷市场的核心因素——借贷利率,是反映社会资金供求关系的重要价格体系,其水平的高低关系到民间借贷市场的健康发展,甚至关系到社会的和谐安定。目前以利率定价为基础的民间利率分析方法,成为学术界和实业人士关心的焦点。但目前国内对民间借贷利率的研究还处于起步阶段,对利率的定价模式等需要进一步研究。民间借贷利率是一个多因素决定的变量,主要是由贷款管理成本、贷款机会成本及贷款风险溢价构成。[1]此外民间借贷利率受货币政策工具、资产价格的影响;民间借贷的期限与民间借贷的利率成负相关;受正规金融信贷约束、借贷双方亲缘关系以及人力资本的影响;还与区域性经济发展状况密切相关。[2-4]
在民间借贷利率影响因素的研究中,魏源[5],宋新乐和魏源[6]通过建立利率定价多元回归模型并进行实证研究得出市场利率能够反映公共信息的影响,贷款人和借款人的各自私人信息中相关风险和财务能力因素影响着民间借贷市场上的利率定价。Aleem[7]指出影响巴基斯坦民间借贷资金价格的主要因素是贷款成本,由于存在着严重的信息不对称和高风险,其利率水平较高。Hoff和Stieglitz通过模型证明随着贷款者数量增加,贷款者每笔贷款规模将会随之减少,相应地,甄别成本和执行成本就会增加,一旦边际成本大于边际收益,贷款者就会提高相应的贷款利率。[8]由于民间借贷的融资活动缺少监管,并且缺少合格的担保和抵押,因而就存在借款违约的风险。Bhattacharjee和Monojit指出民间借贷利率受地区发达程度影响,其主要原因是欠发达地区的放贷人中介数较少,尤其是了解借款人的中介少,加速了垄断权力的增强。[9]单惟婷和沈洪斌选取温州为案例,运用实证分析得出商业银行贷款利率对民间借贷利率的影响非常大。[10]辛兵海和康永辉运用双边随机边界模型分析了农户和放贷者的议价能力,分析结果表明农户个体特征如贷款担保提供情况、家庭主要收入来源以及为取得贷款的额外花费等影响双方的议价能力。[11]有的学者用垄断的市场结构原理,分析出民间借贷会形成高利率,而市场的分割,特殊主义的存在强化了垄断的程度。[12-13]
目前对民间借贷的研究领域主要在民间借贷影响因素、形成高利率的原因与政策指引等方面,很大程度上只是理论方面的研究,还没有模型具体研究民间借贷机构利率如何定价。而民间借贷利率能否精算定价?采用何种模型进行定价?这些都是有益的尝试。
针对这些问题,本文主要探讨保险精算思想在民间借贷机构利率定价理论中的应用,分析利用Black-Scholes模型验证民间借贷利率是否能够精算定价。在民间借贷市场上,民间借贷利率溢价是需求方补偿由于未来还款而给供给方造成的经济损失,而在保险市场上利率溢价为被保险人为未来获得赔偿而向保险公司支付的保费,这为本文运用保险精算方法解决民间借贷利率定价问题提供了理论依据。保险精算方法的基本原理是保险期内纯保费收入的现金价值与支出保险金的现金价值相等,其定价原则是未来实际发生的损失与估计的期望损失值相等,每个投保人应交的保费与其分担的损失期望值相等。从保险精算的角度,将期权价格看作是公平保费具有其合理性[14],利用保险精算方法研究期权问题是一个有益的尝试[14-15],本文期望利用精算原理推导民间借贷机构利率定价模型。
与以往研究相比,本文的贡献主要体现在:扩充了民间借贷机构利率定价的研究方法,通过引入保险精算定价方法,利用Black-Scholes模型验证民间借贷利率是否能够精算定价;实证结果表明依据Black-Scholes模型计算出来的民间借贷机构理论利率与实际利率吻合度良好,反映了实际情况下的民间借贷机构的市场利率。
二、民间借贷机构利率精算定价Black-Scholes模型构建
保险定价时,无本金投入,是先发生定价,一次性收取当期保费,损失由赔付体现,保险人在收取保费与支付损失之间存在着时间差。而民间借贷在保留条款(如利率随着国家公布利率浮动)下定价完成后,借出本金,利息分期收取,损失由利息或本金体现,贷款人在收取利息与认定损失之间存在着时间差。因此,在保险精算学原理基础上,我们确定民间借贷精算定价公式,其假设与保险定价有两点不同:一是因为民间借贷业务的随机特性,风险较高(这也是与正规金融机构的最大不同),其价格服从一定漂移率与波动率的Brown运动,风险报酬率体现在隐含着对未来回款的风险估计利率溢价,用利率附加费表示。二是民间借贷机构利率定价还需要考虑到期回不了款的违约风险,这里用考虑违约风险的未来现金流精算现值表示。
因此,我们可以确定一个基于Black-Scholes的民间借贷机构利率定价模型V=民间借贷机构基础利率、附加费和到期日支付的现金流现值之和,即v=B(S(t),t)+A(F(t),t)+C(r,t),其中B(S(t),t)代表民间借贷机构基础利率,A(F(t),t)表示民间借贷机构利率附加费,C(r,t)代表民间借贷机构现金流支付现值,各部分推导过程如下:
(一)民间借贷机构基础利率
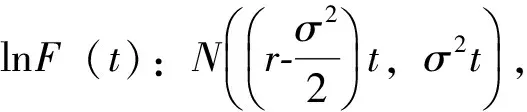
(1)
用精算方法推导民间借贷机构基础利率应等于还款时导致潜在损失和请求权的数学期望,则公式为:
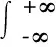
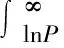
(2)
将(1)代入(2)整理得:B(F(t),t)=FtN(-d1)+Pe-r(T-t)N(-d2)
其中N(*)为标准正态分布累积分布函数,
(3)
(二)民间借贷机构利率附加
民间借贷机构利率定价除了基本的定价外,还包括为各种风险而索要的风险溢价,即民间借贷机构利率附加。附加费隐含着对未来回款的风险估计,因此附加费在数值上相当于民间借贷机构价格的时间价值,而民间借贷机构价格的时间价值等于在任意时刻τ回款的民间借贷机构价值减去内在价值后的剩余部分,则附加费A(F(t),t)用公式表述为At(F(t),t)=A(F(t),t)-max(Ft-Pe-r(T-t),0)。根据上文的论述,保险精算方法就是从评估保险人的潜在损失和相应的概率分布入手,然后将其代入到期权未来报酬(损失)的期望值,运用凑微分进行推导,最后以无风险利率进行折现求得。
同理可得:
At(F(t),t)=FtN(d3)-Pe-r(T-t)N(d4)
式中,N(*)为标准正态累积分布函数
A(F(t),t)=FtN(d3)-Pe-r(T-t)N(d4)-max(Ft-Pe-r(T-t),0)
(4)
(三)到期日民间借贷机构现金流支付现值计算


(5)
(四)基于Black-Scholes的民间借贷机构利率定价模型
综上,基于Black-Scholes的民间借贷机构利率定价模型为
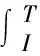
(6)
式中,N(*)为标准正态累积分布函数
(7)

其中:t代表模型中距离到期日时间即贷款期,V代表借款人在期间发生的资产的市场价值,σ代表贷款期内借款人的资产市场价值的波动率,r代表贷款期内的无风险利率,N(*)代表正态分布累积概率。
三、实证检验
(一)数据选取
本文以深圳某租赁公司2013-2016年的201家贷款企业作为实证研究的样本。由于在计算精算模型厘定产品的费率时,其前提假设要求历史数据要有可比性、一致性和同质性。还有在概率统计运算中,各个组合保单间要具备互相独立性的性质。因此本文在选取数据时,要充分考虑到各种假设前提,避免由于数据选取不当而使结果不合适。数据选取时由于每个地区环境不同,进而形成的信用程度也不同。考虑到本文将信用风险加入到民间借贷机构利率的定价模型中,故选择不同信用等级的民间借贷机构贷款数据作为实证样本。本文将民间借贷机构的借款客户分类为正常、关注、次级、可疑、损失。贷款数据分类情况见表1。

表1 民间借贷机构贷款数据的基本情况
(二)模型参数估计
1.借款数P
根据有限责任公司的债务价值的确定,它是公司自身的资产价值扣除留存收益即分配给股东的收益,由于其可以看作期权,不论它的性质和期间如何,不变的是它的执行价格。在民间借贷机构市场中,本研究将P的估计价值认定为资产负债表中的负债总额即贷款人向贷款公司的借款数。
2.资产价格F
在股权市场中,不管运用何种模型对股票评估价值时,标的资产的价格就是公司的价值,因为它是在交易过程中对市场的无偏差评估的价值,因此可以将公司的价值看作公平的市场价值。所以在民间借贷机构市场中对某个借款人的贷款保险可以看作对此借款人总负债保险的一部分,贷款保险期则是该期权距离到期日的时间,保险人则可以认为是期权的卖方,期权的买方为借款人的债权人;贷款保险到期类似看跌期权到期,标的资产的价值可以看作是民间借贷机构的价值。
3.距离到期日的时间t
代表贷款租期数,t代表贷款保险期(模型中距离期权到期日的时间),对于每一个贷款者而言未还租期不同,即期权到期日不同。然而为了下文的实证对比,我们有必要对距离到期日的时间t做出合理的估计,因此本研究将距离到期日的时间t设为相近的日期。
4.无风险利率r
在美国等债券市场发达的国家,无风险利率通常是到期日相同的短期国债利率,然后结合市场风险利率计算出的估计值,就可以作为市场风险溢价收益率。在以往的定价模型中,学者均假设贷款存续期间的无风险利率是固定不变的。而在本文建立的模型中,无风险利率是重要的影响因素且是未知的,而民间借贷机构中利率不是固定不变的,存在风险溢价,所以为了计算方便,减少未知变量的个数,本文将无风险利率设定为已知数,将无风险利率估计为政府短期债券的利率。由于利率有一定的期限结构,可选取在期限内相对稳定,且与我们上面选取的民间借贷机构数据到期时间相同的一类政府利率作为民间借贷机构利率定价模型中的无风险利率的评估价值,通过财政部发行的记账式国债期限将其作为民间借贷机构利率定价模型的无风险利率r的估计。
5.波动率σ
在民间借贷机构利率定价模型中我们看到波动率σ是影响利率定价的重要因素。波动率是有关联的价格的变动概率及幅度。波动率可分为两种:一种是历史波动率,它是根据已经公布的股价历史资料计算得出的收益率的标准差。另一种是根据定价模型由市场中标的资产的现价反推出波动率,我们称为隐含波动率。本文采用历史波动率来求样本数据的理论价格。我们作了这样的假设:历史数据计算出的历史波动率在以后不会产生比较大的变动幅度,并且这种不变的波动会延续到未来,因此对于未来的价格波动率计算,我们可以通过结合历史资料数据计算而得的波动率而得。波动率σ计算公式如下:

(8)
6.违约强度λ
λ是泊松分布的参数,只要是随机事件,那么在单位时间内它发生的次数是可以计算出来的,那么λ就是服从泊松分布的任何随机事件在单位时间的平均发生率。KMV模型就是运用期权定价理论的模型和思想,首先根据公司的股市价值来推测它的资产市场价值和资产收益的波动性,然后在此基础上从而推算出违约距离和预期违约率。本文将基于模型,按照这个思路,先计算出资产的市场价值以及资产收益的波动性,然后得出贷款公司违约距离和理论预期违约率,以此来度量贷款公司的信用风险。但是,对于多数研究此现象的学者来说,预期违约率和违约距离之间的函数关系因为违约历史数据较难取得而没办法构建。因此可以基于某种假设条件,在假设的前提下计算理论上的违约率。该违约率的计算需要公司资产价值首先服从几何Brown运动,其次资产收益也要服从标准正态分布。于是,可以进一步得到:违约率可以用正态累积概率来表达,按照KMV 方法,将贷款机构收入的变化设定为服从正态分布,进而该贷款机构收入服从标准对数正态分布,就可获得贷款机构的理论违约概率EDF( Expected Default Frequency) 为:
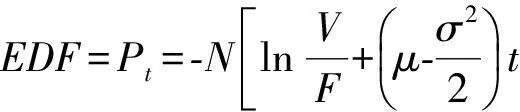
(三)实证应用及结果分析
1.基于Black-Scholes的民间借贷机构利率精算定价模型的运算
首先,为便于民间借贷机构利率精算定价模型的计算,本文做出如下基本假设:
假设 1,在不存在其他导致违约的因素的情况下,借款人只会因为自身资产的市场价值低于负债价值才会导致贷款违约。
假设 2,借款人的总负债在贷款保险期内不会发生较大的波动稳定且未来的时间内保持不变。
假设 3,基于贷款期限和保险期限不会随意变更的特点,将距离到期日的时间t设为近似数。
假设 4,保险的贷款金额是到期日应该收回的贷款本金。
假设 5,无风险利率可以用贷款保险期内到期日相同的短期国债利率来近似。
其次,对基于Black-Scholes的民间借贷机构利率精算定价模型的运算
第一步:根据公式(8)运用迭代计算贷款机构2013、2014、2015、2016年的价值波动率。
第二步:根据公式(9)计算违约强度。
第三步:根据公式(6)和(7),运用Matlab编程,在Matlab软件下运行相应的程序,求解公式。
2.基于Black-Scholes的民间借贷机构利率精算定价模型的计算结果
应用Matlab软件,通过数值计算方法,可以得到民间借贷机构的理论利率,远远高于民间借贷机构的实际利率。根据计算的模型利率,将其与机构公布的利率比较,可以更好更清楚的进行下文的分析。见下图。
为考查民间借贷机构实际利率与理论利率的偏差幅度,我们进而通过偏离度指标对前面数据进行检验。偏离度=(实际利率-理论利率)/理论利率,民间借贷机构实际利率相对于理论利率的偏离幅度如图所示。显然,在大多数借贷企业的理论利率远远高于其实际利率。

图1 民间借贷机构实际利率与理论利率的比较
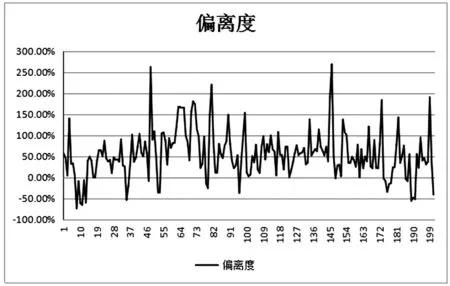
图2 实际利率相对于理论利率的偏离幅度
3.基于Black-Scholes的民间借贷机构利率精算定价模型的结果回归分析
针对201家民间借贷机构客户的理论利率与市场利率进行 Lin(一元线性)、Log(对数函数)、QUA(二次函数)、CUB(三次函数)的拟合回归。理论利率为自变量 X,市场利率为因变量 Y。从拟合回归的检验结果及效果图中可以看出,CUB(三次函数)函数的拟合程度更好反应理论利率与实际利率的对应关系。拟合回归结果及效果图见图3。
从上面分析中可以看出,民间借贷机构的实际利率与理论利率偏差过大,并存在较大的套利空间。通过实证检验发现,机构理论利率远远高于其实际利率,实际利率相对于理论利率的偏离度在大部分在100%内。但是也有超出正常的偏离范围幅度较大的,全部201个样本中,有9个样本偏离率较大。
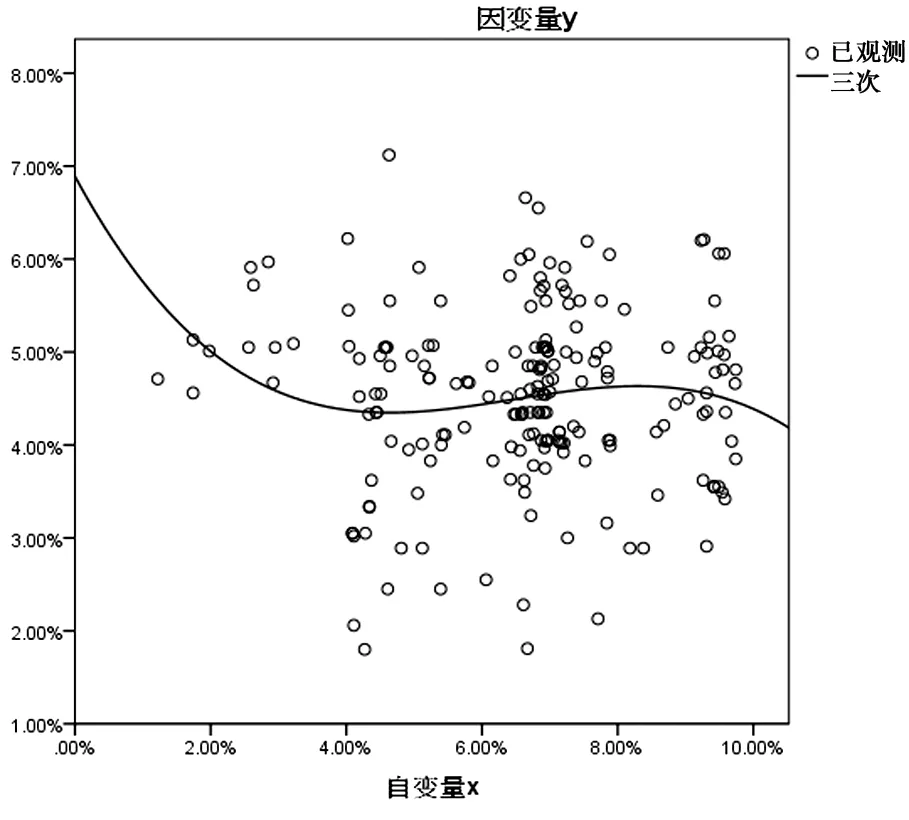
图3 回归效果图
4.民间借贷机构理论利率与实际利率存在偏差的原因分析
基于Black-Scholes的民间借贷机构利率精算定价模型能够近似的反映民间借贷机构的利率,即其理论利率,但由于模型局限实际利率与理论利率存在一定偏差也完全正常。对于信用评级较低的这类企业,因为存在着较大的信用违约风险。从而导致得出的理论利率与实际利率有一定的计算误差。
理论利率与实际利率之间存在一定的偏差,这是由于目前民间借贷机构利率定价还没有完全实现市场化,不能真实反映市场的情况,从而导致其价格与价值的偏离;其次现实市场条件并不完全满足民间借贷机构利率精算定价模型的假设前提,有些条件是市场无法满足的,比如民间借贷市场上很多借款公司并不都是有担保的,因此其在市场上表现出来不同的违约风险,使得定价出现偏差;而且民间借贷机构的利率常常会受到民间借贷机构的体制及制度、交易市场供求、市场参与者的风险预期等多方面因素的影响,这样也使民间借贷机构理论利率与其公布的实际利率存在一定程度的偏离。
四、基本结论
目前以利率定价为基础的民间借贷利率分析方法,逐渐成为学术界和实业人士关心的焦点,本文引入保险精算定价方法,利用Black-Scholes模型验证民间借贷机构利率是否能够精算定价,并以深圳某民间借贷机构2013-2016年的交易数据为样本,检验了该模型对民间借贷机构利率精算定价的影响。结论证明民间借贷机构利率能够精算定价,依据Black-Scholes模型计算出来的民间借贷机构理论利率与实际利率能更好地吻合,更好地反映真实情况下的民间借贷机构的市场利率。通过进一步的分析发现,民间借贷机构的利率偏离比较明显,偏离幅度大多在2%-4%。从市场利率和理论利率回归拟合效果来看,该民间借贷机构的利率没有向一个合理水平靠拢,回归效果不理想。这说明我国民间借贷机构市场定价效率不高,存在着一定的不稳定性。
本文的研究对民间借贷机构利率定价具有一定的指导性意义,但由于民间借贷市场上数据不透明,数据资料的搜集比较困难,该模型尚需进一步的验证和完善;在条件允许的前提下,在样本数据选择上将选取多个地区的数据合并,增加样本容量,使研究更全面,更具科学性,研究结论也会更有普遍性。
参考文献:
[1] Bottomley A.Interest rate determination in underdeveloped rural areas[J]. American Journal of Agricultural Economics, 1980(2):449-464.
[2] 张雪春,徐忠,秦朵.民间借贷利率与民间资本的出路:温州案例[J]. 金融研究,2013(3):1-14.
[3] 徐丽鹤,袁燕. 收入阶层、社会资本与农户私人借贷利率[J]. 金融研究, 2013(9):150-164.
[4] 潘彬, 金雯雯. 货币政策对民间借贷利率的作用机制与实施效果[J]. 经济研究, 2017(8):78-93.
[5] 魏源.中国农村民间借贷市场利率定价模型的经验分析[J].财经问题研究,2013(10):83-90.
[6] 宋新乐,魏源.中国农村民间借贷市场融资约束环境下利率定价模型分析——以广东农村实地调查数据为例[J].统计与信息论坛,2016(4):93-100.
[7] Aleem, Irfan. Imperfect information, screening, and the costs of informal lending: a study of a rural credit market in Pakistan [J]. World Bank Economic Review, 1990(3):329-349.
[8] Hoff K, Stiglitz JE. Introduction: imperfect information and credit markets-puzzles and policy perspectives [J]. World Bank Economic Review, 1990(3):235-50.
[9] Bhattacharjee M, Rajeev M. Interest rate formation in informal credit markets in India: Does level of development matter? [J]. Brooks World Poverty Institute Working Paper, 2010.
[10] 单惟婷, 沈宏斌. 温州民间借贷利率的影响因素实证分析[J]. 上海金融, 2013(10):108-109.
[11] 辛兵海, 廉永辉, 陶江. 我国农村借贷市场借贷双方议价能力测度——基于双边随机边界模型的分析[J]. 农业技术经济, 2014(6):64-73.
[12] 刘静, 郑震龙.我国民间借贷的利率分析[J].云南财贸学院学报,2000(6): 27-31.
[13] 张晓艳.农村民间借贷高利率形成原因及规范对策[J].经济问题,2010(8):67-69.
[14] Bladt M, Rydberg T H. An actuarial approach to option pricing under the physical measure and without market assumptions [J]. Insurance Mathematics & Economics, 1998(1):65-73.
[15] Schmitz N. Note on option pricing by actuarial considerations [J]. Insurance Mathematics & Economics, 2005(3):517-518.
*感谢匿名审稿专家的宝贵建议,感谢研究生谢宁与宋京辉出色的助理研究工作。文责自负。
