汽车发动机曲轴有限元分析及优化设计

贺洋洋， 申 琪， 郭昌盛， 张昌明， 熊 超， 邢 思

(陕西理工大学 机械工程学院， 陕西 汉中 723000)

曲轴是发动机最关键、最主要的运动部件之一，也是最难加工的部件之一。在内燃机工作时，承载着周期性变化的载荷，在复杂的弯曲应力和扭转应力共同作用下，使得曲轴的工作条件格外苛刻，其强度和寿命经受着严重的考验[1]。在曲轴研究方面，国内学者徐中明等人[2]利用仿真技术对曲轴进行了静强度分析，王良国等人[3]对368Q型发动机曲轴进行了疲劳强度有限元分析，李德水等人[4]采用试验方法对小型柴油机曲轴模态进行了试验研究。上述学者主要从试验和仿真的角度来对曲轴进行分析，没有考虑到曲轴几何参数与曲轴应变、应力之间的关系，并且随着发动机技术的发展，曲轴的工作条件日益严酷，需要在设计上合理优化选取曲轴的结构，并根据要求选择合理的尺寸、材料和工艺，以求获得满意的技术经济效果。

综上所述，可以看出曲轴设计的重要性。因此，有必要研究曲轴的几何参数与其应变、应力之间的关系。在充分保证曲轴设计可靠性的前提下，首先考虑到曲轴结构的复杂性，利用CATIA软件强大的曲面建模功能对其进行参数化建模，并结合ANSYS Workbench进行有限元分析得出曲轴的应变、应力分布情况，根据有限元分析结果确定优化参数。最后以减小曲轴最大应变和最大应力作为优化目标，采用Design Exploration中的基于响应面的多目标优化对其参数进行优化设计，从而改善汽车发动机曲轴的整体性能，为实际曲轴加工工艺参数的优化提供依据。

1 曲轴参数化模型与有限元静力学分析

1.1 曲轴参数化模型

鉴于曲轴的结构复杂性，利用CATIA软件强大的曲面造型功能对其进行参数化建模，曲轴参数化模型如图1所示。

图1 曲轴参数化模型图

1.2 有限元静力学分析

曲轴静力学分析是在固定不变载荷作用下计算曲轴的位移和应力，不考虑惯性和阻尼的影响，因此静力学分析可为曲轴结构优化提供重要参考[5-6]。曲轴的受力情况主要参考曲柄连杆机构的受力分析。曲柄连杆在工作冲程中，承受弯曲力的同时又承受着扭转力，可以说曲轴工作环境极度苛刻和复杂[7-9]。此次研究的曲轴材料采用球墨铸铁，密度ρ=7.8×10-9kg/mm3，弹性模量E=1.0×105MPa，泊松比μ=0.23，为了使分析结果更加接近实际情况，设置体网格尺寸为2 mm，经网格化分后得到了参数化的有限元模型,划分结果比较理想，如图2所示。在模拟工况下曲轴的受力情况如图3所示，对曲轴模型进行有限元静力学分析，得到应变和应力分布结果如图4所示。

图2 网格划分后的有限元模型 图3 曲轴载荷与约束施加图

(a) 应变分布云图 (b) 应力分布云图 图4 曲轴的应变、应力分布云图

从图4中可以看出，曲轴的最大变形量约为0.090 6 mm，主要集中在第二、三曲柄处；曲轴的最大应力发生在主轴颈以及连杆轴颈与过渡圆角处，且其值为65.691 MPa。曲轴其他部分的应变量和应力值相对较小，表明曲轴结构满足刚度要求，使用安全性高，满足设计的要求。

2 曲轴的优化设计

2.1 优化尺寸选择

根据上述有限元静力学分析结果，并结合Design Exploration中的基于响应面的多目标优化，对主轴颈半径、连杆颈半径以及过渡颈圆角这3个尺寸进行优化设计。对于曲轴结构局部尺寸的修改并不会影响曲轴的整体尺寸，因此可对曲轴局部尺寸进行优化设计，进而实现曲轴应变和应力的减小。在不影响曲轴性能的前提下确定优化尺寸的变化范围，并保证在优化过程中各个优化尺寸不发生冲突，且确保模型在优化过程中可再生。优化尺寸的初始值和变化范围如表1所示。

表1 优化分析时具体参数及变量优化参数范围(采用默认设置)

2.2 优化尺寸灵敏度分析

图5 优化尺寸灵敏度分析图

优化尺寸灵敏度分析是利用灵敏度值的变化大小来反映各个参数对目标值的影响程度，从而根据灵敏度值的大小和正负来对曲轴进行优化设计[10-14]。结合Six Sigma(六西格玛)的判定原则，最终确定哪些尺寸对曲轴性能的影响起决定性作用。通过调取局部灵敏度图，可以查看优化设计时所选的设计变量对曲轴的应变和应力的影响程度。从灵敏度图中可以直观的看出设计点对输出参数的敏感性程度，两个优化目标与3个输入变量的敏感程度如图5所示。

由图5可以看出，参数P1-DS_RM(主轴颈半径)和P2-DS_RC(连杆颈半径)的灵敏度值都是负值参数，表示P1-DS_RM和P2-DS_RC值的增加会使曲轴的应变和应力减小；参数P3-DS_FC(连杆颈圆角)的灵敏度值为正值参数，表示P3-DS_FC值的增加会使曲轴应变和应力增大，并且参数P3-DS_FC对曲轴的应变和应力影响最大。综合以上因素分析，优化结果主要是通过改变主轴颈半径、连杆颈半径与过渡圆角来达到优化的目的。

2.3 优化尺寸响应图分析

利用ANSYS Workbench平台中的Design Exploration模块对曲轴进行优化设计。在对曲轴进行优化设计的过程中，不需要反复修改模型的尺寸参数，只需设置好曲轴的设计变量以及响应参数的限定条件，就能对曲轴的结构进行优化设计。以减小曲轴的最大应变和最大应力作为优化目标，采用Design Exploration中的基于响应面的多目标优化对曲轴进行优化设计，从而获得输入参数与输出参数之间的关系，分别如图6和图7所示。

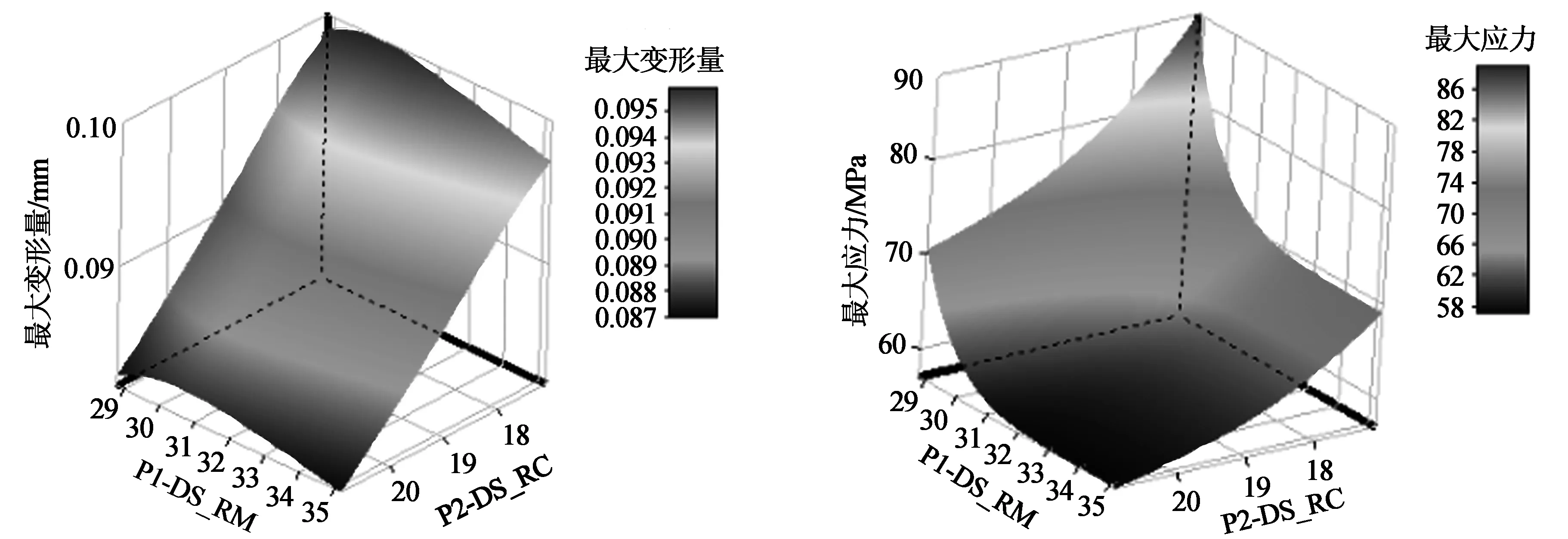
图6 曲轴最大变形与优化参数响应云图 图7 曲轴最大应力与优化参数响应云图

图6和图7分别为设计变量P1-DS_RM、P2-DS_RC和P3-DS_FC对目标函数最大变形和最大应力的响应云图。从图6中可以看出，在给定的变化范围内，曲轴的最大变形对于主轴颈半径和连杆颈半径的敏感性较大，会随着主轴颈半径和连杆颈半径的增大而减小；同理从图7中可看出，最大应力随着主轴颈半径和连杆颈半径的增大而减小。因此，适当地减小主轴颈半径和连杆颈半径可以实现曲轴的最大变形和最大应力的减小。

2.4 优化结果分析

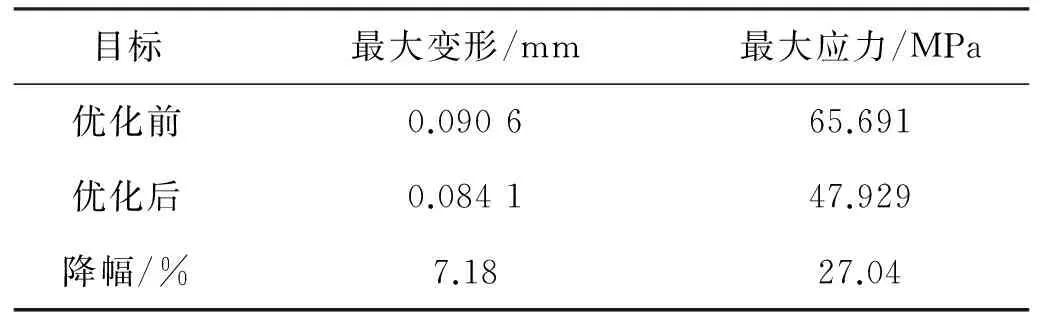
在曲轴的优化设计过程中，采用Design Exploration中的基于响应面的多目标优化求解方法[15]。优化设计的步骤为：首先定义好状态参数以及求解的目标参数，再查找主轴颈半径、连杆颈半径和连杆颈圆角尺寸参数对曲轴强度、刚度等性能参数的影响，最后选择最优结果得到曲轴主轴颈半径、连杆颈半径和连杆颈圆角尺寸作为最合理的设计点，从而得到上述3个结构尺寸的最优化设计方案。优化后的尺寸P1-DS_RM为35.2 mm，P2-DS_RC为20.9 mm，P3-DS_FC为3.309 5 mm；进行圆整后P1-DS_RM为35 mm，P2-DS_RC为21 mm，P3-DS_FC为3 mm。按照圆整后的尺寸对模型进行再生，进而对再生的模型进行有限元静力学分析，其分析结果如图8所示。优化前后曲轴静力学特性参数对比如表2所示。

(a) 应变分布云图 (b) 应力分布云图图8 曲轴优化后的应变、应力分布云图

目标最大变形/mm最大应力/MPa优化前0.090665.691优化后0.084147.929降幅/%7.1827.04

从表2中可以看出，优化后的曲轴最大变形与最大应力都有所下降，且曲轴最大变形量减少了7.18%、最大应力减少了27.04%，但其刚度和强度仍然满足使用要求。因此，优化后曲轴结构的静力学特性得到了显著提高。

3 结 论

利用CATIA软件实现了曲轴参数化建模，并结合ANSYS Workbench实现对汽车发动机曲轴的静力学分析，从而得到了曲轴的应变和应力分布云图。再通过Design Exploration中基于响应面的多目标优化对曲轴3个关键尺寸进行了灵敏度分析及多目标优化设计。通过优化设计得到了曲轴的最优参数：当P1-DS_RM(主轴颈半径)为35 mm，P2-DS_RC(连杆颈半径)为21 mm，P3-DS_FC(连杆颈圆角)为3 mm时为最优解。通过对比优化前后分析数据可知，曲轴的最大变形由0.090 6 mm减少到0.084 1 mm，降低了7.18%，最大应力由65.691 MPa减少到47.929 MPa，降低了27.04%，极大幅度提升了曲轴的静力学性能，达到了预期的效果。通过对汽车发动机曲轴的优化设计，为实际曲轴加工工艺参数的合理选择、优化打下理论基础。

[参考文献]

[1] 张朝辉.ANSYS 8.0结构分析及实例解析[M].北京:机械工业出版社,2005.

[2] 徐中明,牟笑静.基于有限元法的发动机曲轴静强度分析[J].重庆大学学报,2008,31(9):977-981.

[3] 王良国,胡德波.368Q型发动机曲轴疲劳强度有限元分析[J].内燃机学报,2000,18(3):270-274.

[4] 李德水,闫兵,华春蓉,等.小型柴油机曲轴模态试验研究[J].车用发动机,2010(2):89-92.

[5] 牛颖,李全普,于俊光.HDBS-63高速卧式加工中心主轴箱多目标优化设计[J].组合机床与自动化加工技术,2011(6):77-80.

[6] 何树高.大功率柴油机曲轴静强度有限元分析[D].大连:大连交通大学,2009.

[7] 刘波.曲轴参数化建模和有限元分析[D].武汉:武汉理工大学,2006.

[8] 刘利民.曲轴圆角滚压的有限元模拟和试验研究[D].哈尔滨:哈尔滨工程大学,2012.

[9] 王受路.基于ANSYS的曲轴强度有限元分析[D].济南:山东大学,2011.

[10] 陈亚娟,贾志超.摩托车车架轻量化优化设计[J].机械强度,2014,36(3):479-482.

[11] 孙晓东,陈凯.基于ANSYS Workbench的锚杆托盘优化设计与强度分析[J].煤矿机械,2013,34(12):14-15.

[12] 张宏博,薄瑞峰,游小红.深孔钻床床身的拓扑轻量化设计[J].机械设计与造,2014(1):68-70.

[13] 程彬彬,黄美发,吴常林,等.基于ANSYS Workbench的龙门铣床横梁多目标优化设计[J].组合机床与自动化加工技术,2015(2):10-12.

[14] 冯博琳,王军利,贺洋洋,等.新型称重传感器气缸砝码组件设计[J].陕西理工学院学报(自然科学版),2017,33(1):27-32.

[15] 冯博琳,王军利,黄崇利,等.参数化称重传感器标定托架有限元分析及优化[J].陕西理工学院学报(自然科学版),2016,32(6):19-23.