信道转移概率变化下的极化码设计方案
2018-05-02黄志亮张施怡周水红
黄志亮 张施怡 周水红

摘 要: 为了适应实际通信系统中信道随时间的变化,本文将极化码设计推广至更实际的时变通信信道;综合考虑信道变化范围内所有位信道的平均性能,然后选择出平均性能最好的位信道作为极化码的信息位。文章设计了几种用于设计极化码的位信道平均性能算方法和一种衡量平均增益的计算方法。仿真结果表明,这些设计能有效地提高极化码的平均性能;在时变信道中,通过更加细致地设计极化码,能有效地提高极化码的平均性能。
关键词: 极化码; 信道极化; 极化码设计; 转移概率
中图分类号:TN911.2 文献标志码:A 文章编号:1006-8228(2018)03-09-04
Polar code design schemes under Changing Channel Transition Probability
Huang Zhiliang, Zhang Shiyi, Zhou Shuihong
(College of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua, Zhejiang 321004, China)
Abstract: In order to adapt to time-varying channel in actual communication system, in this paper, the design of polar code is extended to more practical time-varying communication channel; considering the average performance of all the bit-channels, the best bit-channels with the best average performance are selected as the information set of the polar code. Several methods to choose the best bit-channels are proposed, and the method for evaluating the average gains of proposed methods is designed. Simulation results showed that the proposed methods can improve the average performance of polar codes.
Key words: polar codes; channel polarization; polar code construction; transition probability
0 引言
自从1948年香农在其开创性的文章中提出信道编码定理以来[1],人们一直在寻找着一种渐近性能达到香农限,同时有着低编译码复杂度,并且能广泛适用于各种不同信道场景的信道编码方案。Arikan在2009年基于信道极化现象构造的极化码可能是第一个能满足上述条件的信道编码方案[2]。从Arikan提出极化码以来,关于极化码的研究就成为信息论和编码领域的一个研究热点。
虽然极化码有着丰富和完善的理论,但其在实际应用中也存在着一些需要解决的问题。除了二进制擦除信道(BEC),其他信道下极化码设计的复杂度为指数级复杂度[2]。文献[3]和[4]利用信道近似的方法,在二进制输入无记忆(B-MS)信道条件下,给出了能逼近实际设计的、具有线性复杂度的极化码近似设计方法。然而文献[3]和[4]中极化码近似设计方法是在信道转移概率保持不变的条件下获得的。至今,关于时变信道转移概率条件下极化码设计方面的研究文献还未见到。
在一些实际通信系统中,信道的转移概率依赖于信噪比。在信噪比变化的场景下,最简单的极化码设计方案就是取平均信噪比点对应的信道。这样设计的缺点是没有考虑其他信噪比点,会损失极化码的平均译码性能。
本文提出了一种构造后设计方案:首先将信噪比区间等概率量化,然后利用文献[3]中的方法构造出各个量化信噪比点对应的位信道,最后综合考虑这些位信道,从而设计出需要的极化码。这样做的好处是,综合考虑了各个信噪比点,使得设计出的极化码有更好的平均译码性能。
1 问题描述
1.1 连续信道的下近似离散信道生成方法
考虑一个二进制输入高斯信道(BiAWGN),其采用BPSK调制,即在发送端的二进制数据位c被映射为传输符号x,x=1-2c。接收端获得接收数据y,y=x+z,其中z为均值为0,方差为σ2的高斯随机变量。
此时,已知x时y的条件分布是一個高斯分布,其概率密度函数为
⑴
其中x∈{-1,+1}。
则对于任意的y,由式定义的概率密度函数有
f(y|+1)=f(-y|-1)
此时,称⑴式定义的信道是对称的。
记由⑴式定义的信道为W,此时信噪比为1/σ2。由于信道W的对称性,可以利用文献[3]中的方法实现信道W的下近似二进制输入离散无记忆(B-DMS)信道的生成方法。具体如下:
记y的似然比λy
则有信道W对称信道容量为:
其中:
令μ=2L为将要生成的下近似B-DMS信道输出集合的元素个数。在λ?1的条件下,C[λ]是λ的单调递增函数。所以对于1?i?L,可以将区间[0,∞]分割成如下L个区间。
定义信道,其中,,转移概率为:
上述定义的信道Q为信道W的下近似信道[1]。可以看出信道Q为B-DMS信道,所以可以通过[3]中的方法设计出Q的下近似极化码,由下近似的传递性知,该极化码也是W的下近似极化码。
1.2 优化问题
给定码长和码率,在实际通信中使用极化码时,极化码的信息位集合一般来说需要固定。这是因为,极化码编码和译码需要用到一致的信息位集合,如果发送端的信息位不固定,而接收端没有信息位集合的信息,就无法解码。
当信噪比1/σ2变化时,则其对应信道的转移概率密度函数f(y|x)和似然比λy也随之变化。则利用上小节方法构造的极化码在不同信噪比点对应的最优信息位集合就不同。然而在实际通信中使用极化码时,极化码只能使用一个信息位集合。因此,在信噪比1/σ2变化的条件下,需要折中考虑所有可能的信息位集合,从中选择一个信息位集合,使得该信息位集合对应的极化码的平均译码性能最优。
假定信噪比的取值区间为[a,b]。给定码长N和码率R,记所有可能的信息位集合组成的集合为S。在信噪比区间内任意一点x∈[a,b],使用信息位集合为A的极化码的译码性能记为Pe(x,A)。记g(x)为信噪比的概率密度函数。得到使上述简单模型的平均性能最优的信息位集合(只考慮极化码的译码性能),需要求解如下优化问题:
⑵
2 极化码折中设计方案
因为有限长度的极化码的译码性能目前只能通过仿真得到,所以⑵式描述的优化问题的最优解目前还无法获得。本节给出该优化问题几种启发式的实现方案。启发式实现方案分为两大类,①构造前设计方案:首先直接找一个折中信噪比点对应信道,然后利用文献[3]中极化码设计方法构造出对应的极化码,作为实际使用的极化码;②构造后设计方案:将信噪比区间进行量化,利用文献[3]中的方法构造出每一个量化点下所有的位信道,然后综合评价这些位信道,获得最后信息位集合、即极化码。
2.1 信噪比均匀分布时极化码折中设计方案
⑴ 构造前设计方案
方案一:取最低信噪比点adB对应的信道用于设计极化码,并作为实际使用的极化码。
方案二:取最高信噪比点bdB对应的信道用于设计极化码,并作为实际使用的极化码。
方案三:取平均信噪比点dB对应的信道用于设计极化码,并作为实际使用的极化码。
⑵ 构造后设计方案
方案四:假定需要构造的极化码的码长为N,信息位集合元素的个数为K。按如下方法生成实际使用的极化码:①对信噪比区间进行量化;②利用文献[3]中的方法构造出每一个量化点对应信道下的N个位信道, 并计算出每一个位信道的评价指标;③分别处理每一个量化点下的N个位信道,依据评价指标,将每一个量化点对应的N个位分为K个信息位(指标最小的K个位信道对应的位)和N-K个冻结位,并统计每一位被分为冻结位的次数;④依据每一位被选择为冻结位的次数,从中选择最大的N-K个对应的指标组成冻结位集合Ac,而对应的信息位集合A下的极化码作为最后实际使用的极化码。
方案四可以表述为下面算法:
[算法1:信噪比均匀分布时极化码构造后设计算法(方案四) 输入:信噪比区间[a,b]、量化点个数q、码长N、信息位个数K和冻结位次数统计向量F=(f1,f2…,fN)=(0,…,0)。
输出:元素个数为K信息位集合。 步骤1:将信噪比区间等距离量化为q个点a,,…,b。
步骤2:i从1到q,
⑴ 利用文献[3]中的方法构造出第i个量化点对应信道下的N个位信道,并计算出每一个位信道的评价指标。
⑵ 依据指标的值,选择N-K个值最大的位信道对应的位为冻结位,记选择出的冻结位集合为B。
⑶ j从1到N,如果j∈B,则fj=fj+1。
步骤3:依据F=(f1,…,fN)的值,从中选择最大的N-K个F的分量对应的下标组成冻结位集合Ac,而对应剩下的位组成信息位集合A。 ]
2.2 方案复杂度分析
构造前设计时相当于只有一个量化点,其复杂度就是极化码设计的复杂度。因此,利用文献[3]的近似设计方法,构造前设计方案的复杂度为线性复杂度。构造后设计方案的复杂度和量化点的个数成正比,若记量化的个数为q,极化码设计的复杂度为O(N),则方案的复杂度为qO(N)。一般量化点的个数q为一个比较小的常数,所以构造后设计方案的复杂度也为线性复杂度。
3 仿真结果
为了更好地分辨误帧率(FER),本文的仿真图中将横坐标分成两部分表示,这样将纵坐标“拉近”可以更清晰地显示出各种方案设计的极化码的误帧率的区别。
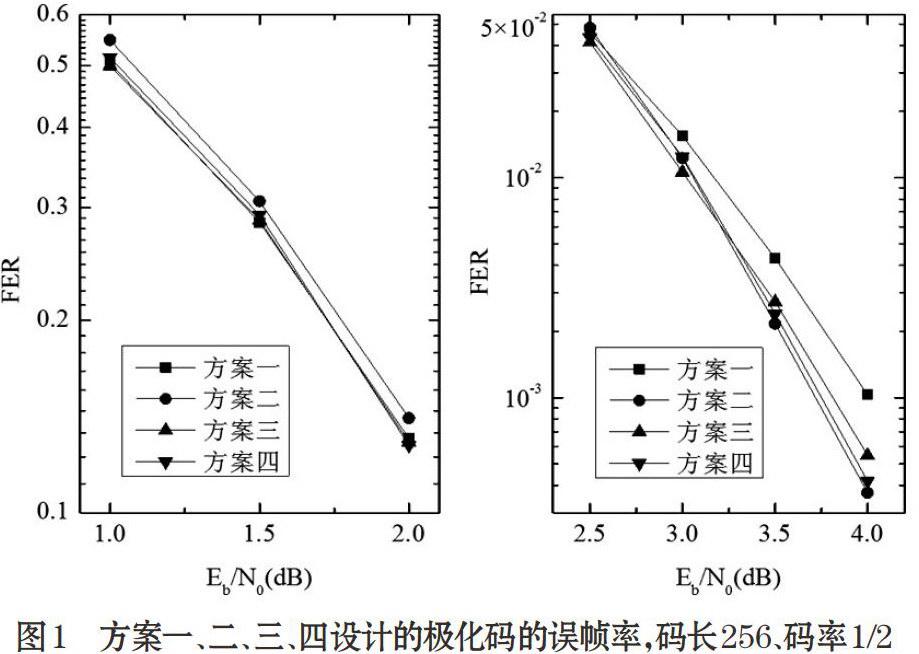
图1给出方案一、方案二、方案三和方案四设计的码长N=256,码率为1/2的极化码在SC译码算法下的误帧率曲线。信噪比区间为[1,4],方案一、二、三分别对应的用来设计极化码的信噪比点是1dB、4dB、2.5dB。需要注意的是:在构造方案四的极化码时,多选取了两个更高的信噪比点4.5和5.0 dB执行算法1,即此时参与算法1的量化点为{1.0,1.5,2.0,2.5, 3.0,3.5,4.0,4.5,5.0}。从仿真结果看,这个调整可以增加方案四在高信噪比区域的译码性能,而对于低信噪比区域影响不大。
图1 方案一、二、三、四设计的极化码的误帧率,码长256、码率1/2
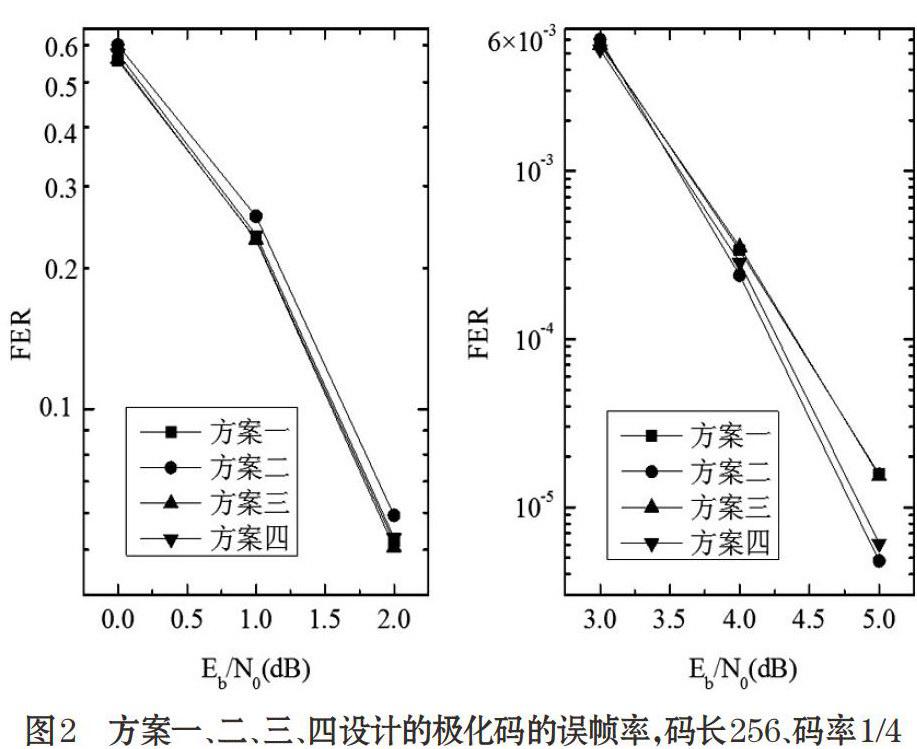
图2 方案一、二、三、四设计的极化码的误帧率,码长256、码率1/4
从图1可以看出,方案一在低信噪比时有较好的译码性能,而在高信噪比时译码性能有一定的损失。方案二正好相反,在高信噪比时有较好的译码性能,而在低信噪比时译码性能有一定的损失。这与直观一致,因为方案一是在最低信噪比1dB时设计得到,而方案二是在最高信噪比4 dB时设计得到。方案三有着比方案一、二更好的平均性能。相比于方案三,方案四在中间信噪比区域有一定的译码性能损失,而在信噪比的两端区域有超过方案三的译码性能,表明了方案四有着比方案三更好的平均性能。
图2给出方案一、二、三、四设计的码长N=256,码率为1/4的极化码在SC译码算法下的误帧率曲线。信噪比区间为[0,5],方案一、二、三分别对应的用来设计极化码的信噪比点是0dB、5dB、2.5dB。对于方案四,参与算法1的量化点为{0.0,1.0,2.0,3.0,4.0,5.0}。
直观上看,方案一在低信噪比区域应该有最好的译码性能,方案二在高信噪比区域有最好的译码性能,方案三在中间信噪比区域有最好的译码性能。图1和图2中的仿真结果和直观一致。从图1和图2可以看出,构造后设计方案四,在低信噪比区域和方案一有差不多的译码性能,在高信噪比区域和方案二有差不多的译码性能,在中间信噪比区域和方案三有差不多的译码性能,表明了方案四良好的平均译码性能。
图3 方案一、二、三、四设计的极化码的误帧率,码长1024、码率1/2
图3给出了方案一、二、三、四设计的码长N=1024,码率为1/2的极化码在SC译码算法下的误帧率曲线。信噪比区间为[1,4],方案一、二、三分别对应的用来设计极化码的信噪比点是1dB、4dB、2.5dB。与图 1一样,在构造方案四的极化码时,多选取了兩个更高的信噪比点4.5和5.0dB执行算法1,即此时参与算法1的量化点为{1.0,1.5,2.0,2.5,3.0,3.5,4.0,4.5,5.0}。从仿真结果看,这个调整可以增加方案四在高信噪比区域的译码性能,而对于低信噪比区域影响不大。
在图3中,方案一、二在低信噪比区域和高信噪比区域的译码性能有着很大的区别,表明了折中设计极化码的必要性。相比于方案一、二、三,方案四有着更好的平均性能。
方案一、二在低信噪比区域和高信噪比区域的译码性能有着很大的区别,表明了折中设计极化码的必要性。相比于方案一、二和三,方案四有着更好的平均性能。
表1给出了三个极化码在四种方案下的“平均度量”。首先假设每个信噪比点的重要程度相同,基于此假设本文设计了一个“平均度量”来衡量方案的好坏。各个方案“平均度量”以及增益的计算方法如下。
⑴ “平均度量”计算方法:首先计算方案四的“平均度量”,对于一个给定的极化码,将其在各个信噪比点的误帧率通过放大或缩小,使其值在1到10之间,然后将所有信噪比点的误帧率值相加,得到方案四的“平均度量”。然后以方案四的放大/缩小倍数作为基准,去放大/缩小其他方案的误帧率,然后将所有信噪比点的误帧率值相加,得到方案一、二、三的“平均度量”。显然“平均度量”的值越小越好。
⑵ “增益”计算方法:对于一个给定的极化码,选取方案一、二、三中的最小“平均度量”,然后计算方案四与该最小“平均度量”相对百分比。
如表1所示,方案四相比于方案一、二、三,有一定的增益,并且方案四的“平均度量”最稳定即:其他方案有可能针对某一个极化码很好,而对另外极化码则相对较差。
表1 方案一、二、三、四设计极化码的“平均度量”
[平均度量 256, 1/2 256, 1/4 1024, 1/2 方案一 29.3 36.6 80.7 方案二 21.9 28.9 40.8 方案三 22.3 36.7 43.5 方案四 21.2 27.5 38.0 增益 3.2% 4.8% 6.9% ]
从上述仿真结果中,可以得到如下结论,在所有提出的方案中,基于冻结位次数的构造后设计方案有着最好的平均译码性能。
4 总结
本文研究了信道转移概率变化下极化码的折中设计问题。本文首先指出了当信道转移概率变化时极化码的设计困难,并建立了一个适合于讨论信道转移概率变化时,如何较优设计极化码的简单模型;然后提出了两类折中设计极化码的方案:构造前设计方案和构造后设计方案。构造前设计方案直接找一个折中信噪比点对应的信道,然后利用极化码的近似设计方法设计出对应的极化码,作为实际使用的极化码;构造后设计方案:将信噪比区间进行量化,构造出每一个量化点对应的位信道的近似信道,然后综合评价这些位信道,获得最后信息位集合,即极化码;最后简要分析了两类方案的复杂度,并给出了仿真结果。
构造前设计方案的复杂度就是极化码设计的复杂度,利用文献[3]的近似设计方法,构造前设计方案的复杂度为线性复杂度。构造后设计方案的复杂度是构造前设计方案的q倍(q为量化点的个数)。一般量化点的个数q为一个比较小的常数,所以,构造后设计方案的复杂度也近似为线性复杂度。
在信噪比均匀分布的条件下,构造前设计方案中提出了三种方案。仿真结果表明,方案一、方案二在低信噪比区域和高信噪比区域的译码性能有很大的区别,表明了折中设计极化码的必要性。构造后设计方案只提出了一种方案即方案四,通过比较方案三和方案四,可以得到构造后设计方案比构造前设计方案有更好的平均性能。
参考文献(References):
[1] Shannon C E. A mathematical theory of communication[J].
Bell Syst. Tech. J.,1948.27:374-423,623-656
[2] Arikan E. Channel polarization: a method for constructing
capacity-achieving codes for symmetric binary-input memoryless channels [J]. IEEE Trans. Inform.Theory,2009.55(7):3051-3073
[3] Tal I, Vardy A. How to construct polar codes[J].IEEE
Trans. Inform.Theory,2013.59(10):6562-6582
[4] Tal I, On the Construction of Polar Codes for Channels
With Moderate Input Alphabet Sizes[J]. IEEE Trans. Inform.Theory,2017.63(3):1501-1509
