Phase Properties of Photon-Added Coherent States for Nonharmonic Oscillators in a Nonlinear Kerr Medium

F.Jahanbakhsh and G.Honarasa

Department of Physics,Shiraz University of Technology,Shiraz,Iran

1 Introduction

The standard coherent state is a particular kind of the quantum states,which its dynamics is similar to oscillatory behavior of a classical harmonic oscillator.[1]These states are defined by the annihilation and creation operators of the harmonic oscillator.Some quantum mechanical systems can be described by the nonharmonic potentials.[2−3]The Gazeau-Klauder coherent state of the anharmonic oscillator has been introduced by Roy.[4]Also,the coherent states for nonharmonic oscillators using generalized Heisenberg algebra have been constructed.[5]

Construction and generation of the nonclassical states is one of the most exciting subjects in quantum optics because their applications in the fields of quantum information processing and quantum computation.Therefore,with the aim of finding nonclassical states many generalizations on the standard coherent states have been nominated.One of the most important generalizations is the photon-added coherent states.[6]The photon-added coherent states can be considered as the nonlinear coherent states with certain nonlinearity function.[7]Also,the photon-subtracted and photon-added coherent states corresponding to the inverse bosonic operators have been introduced in 2004.[8]Furthermore,Zavatta et al.produced the single photon-added coherent state|α,1⟩experimentally in 2005.[9]A method for generating the two photonadded coherent state|α,2⟩has been suggested by Kalamidas et al.[10]The photon-added coherent states and their generalizations have received considerable attention in recent years.[11−14]Roman-Ancheyta et al.constructed deformed Photon-added nonlinear coherent states for a onemode field in a Kerr medium.[15]

Recently,the photon-added coherent states for nonharmonic oscillators in a nonlinear Kerr medium have been introduced by Al-Rajhi using generalized Heisenberg algebra.[16]In the present paper,the phase properties as well as the number-phase entropic uncertainty relation of these states are investigated.For these purpose,the photon-added coherent states for nonharmonic oscillators are reviewed in Sec.2.The Wigner distribution function corresponding to these states is investigated in Sec.3.Then their Pegg-Barnett phase distribution function is studied in Sec.4.Also the number-phase squeezing is discussed in Sec.5.Finally,the number-phase entropic uncertainty relation of these states is investigated in Sec.6.

2 Photon-Added Coherent States for Anharmonic Oscillators

The Hamiltonian for anharmonic oscillators can be expressed by[4]

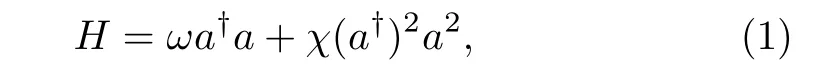
where χ is the coupling constant corresponding to nonlinear susceptibility χ(3)of the Kerr medium.Here a(a†)is the bosonic annihilation(creation)operator.This Hamiltonian describes a one-mode field of frequency ω in a Kerr medium with anharmonicity parameter χ and obeys the equation

with following eigenvalues

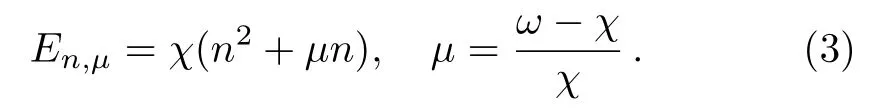
Analogousto the standard photon-added coherent states,[6]the m photon-added coherent states for anharmonic oscillators in a nonlinear Kerr medium are defined as[16]

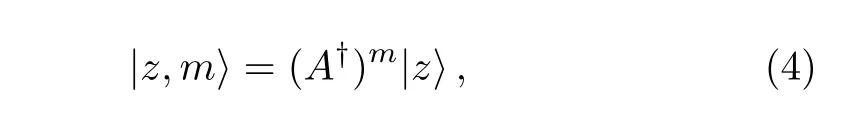
where

is the generalized coherent state for anharmonic oscillators and A†is the generalized creating operator of the generalized Heisenberg algebra.[16]Finally,the photon-added coherent states for anharmonic oscillators can be expressed as follows:[16]

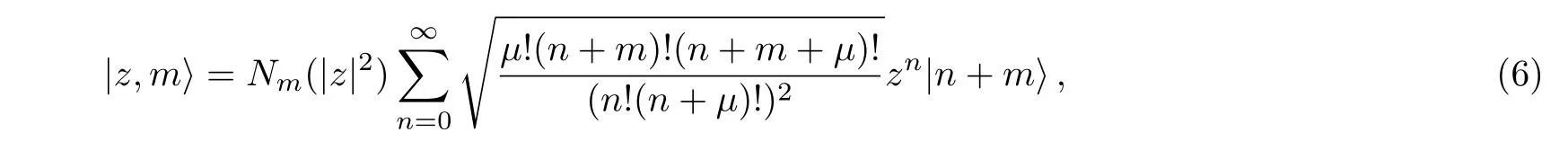
where the normalization constant Nm(|z|2)is obtained as

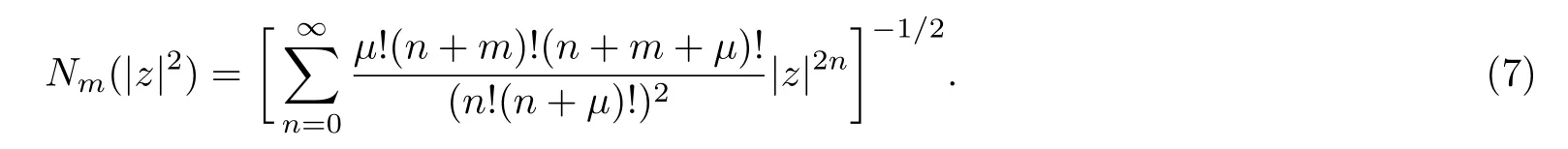
3 Number-Phase Wigner Function

Fig.1 Plot of the number-phase Wigner function associated with the photon-added coherent states for anharmonic oscillators with|z|=1 andµ=1 for(a)m=0,(b)m=1,(c)m=3 and(d)m=5.

The number-phase Wigner function characterizes the quantum statistics of the photons and phase observable of a quantum state.This distribution function may be negative in some regions of number-phase space for specific quantum states that represents the nonclassical signature of these states.The number-phase Wigner operator can be expressed as follows:[17−18]

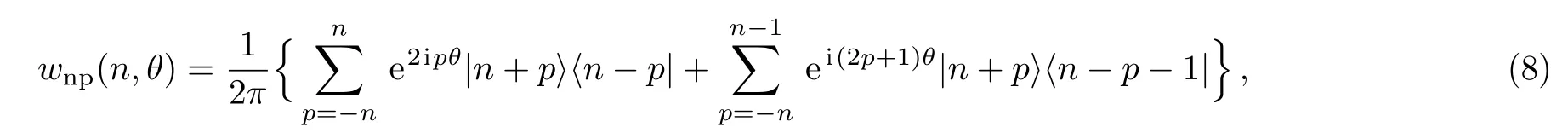
where n=0,1,2,3,...and θ is a real value parameter.The second sentence in the bracket considered to be zero for n=0.Then number-phase Wigner function for a state is defined as the expectation value of the number-phase Wigner operator.The number-phase Wigner function associated with the photon-added coherent states for anharmonic oscillators may be defined as

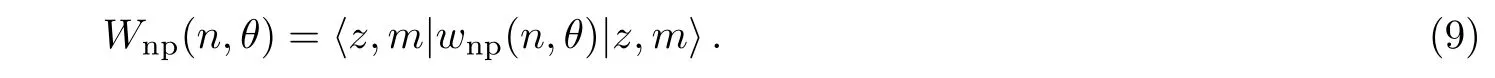
Finally,by using the state(6)in(9),leads to

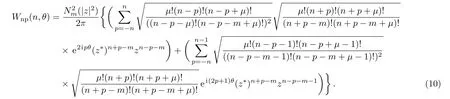
In Fig.1,the number-phase Wigner distribution function has been plotted versus two new variable x=ncos(θ)and y=nsin(θ)for different values of photon added number m.The figure is drawn as curves of constant integer n(concentric rings)crossed by curves of constant θ(radial lines).It is clear that the Wigner function is negative in some regions for all values of m and this represents these states are nonclassical states.

4 Pegg-Barnett Phase Distribution Function

Based on Pegg-Barnett method,a complete set of s+1 dimension phase state are well-defined by[19]

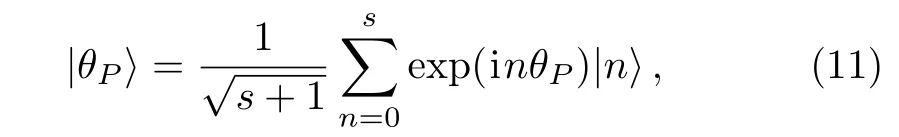
where θPis obtained by

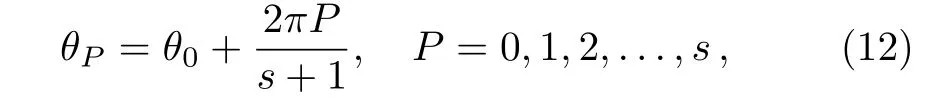
with θ0is an arbitrary value.Also,the Hermitian phase operator corresponding to the phase state(11)is given by

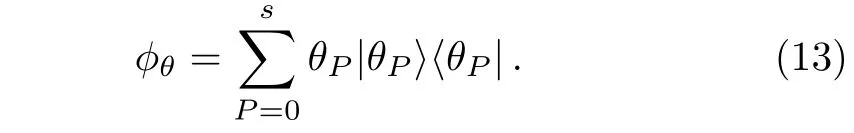
The Pegg-Barnett phase distribution function of the photon-added coherent states for anharmonic oscillators in a nonlinear Kerr medium may be defined as

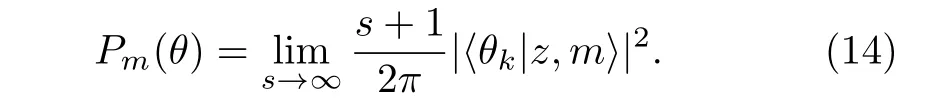
So,by using(6)and(11)in(14),the Pegg-Barnett phase distribution function P(θ)is obtained as follows

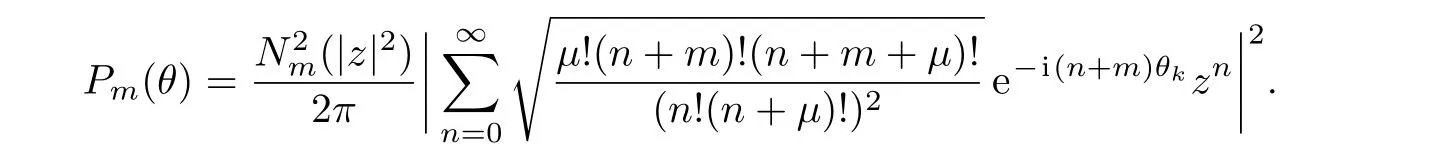
By separating the sentences related to n=l and n≠l,the following relation for phase distribution function can be obtained

Fig.2 Pegg-Barnett phase distribution function associated with the photon-added coherent states for anharmonic oscillators versus θ with|z|=2 and µ =2 for m=1(solid curve),m=3(dashed curve)and m=5(dot-dashed curve).

Figure 2 shows the Pegg-Barnett phase distribution function of the photon-added coherent states for anharmonic oscillators against θ for different values of m.The curves in this figure show there is only a single peak at θ=0.

Furthermore,the distribution function has higher and sharper peak for greater values of photon added number m and thus,it is more localized with respect to θ.

5 Number-Phase Squeezing

The phase and number operators are conjugate to each other and consequently,satisfy the following uncertainty relation

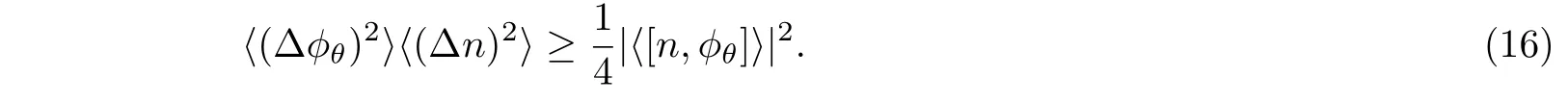
The displacement relation between these operators is given by[n,ϕθ]=i[1 − 2πP(θ)].[19]The phase and number variances associated with the photon-added coherent states for anharmonic oscillators are given by

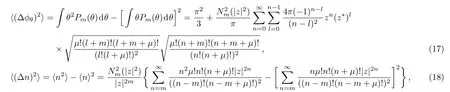
whenever ⟨(∆n)2⟩<1/2|⟨[n,ϕθ]⟩|or ⟨(∆ϕθ)2⟩<1/2 ×|⟨[n,ϕθ]⟩|,the squeezing happens in the number or phase operator,respectively.In order to investigate the squeezing in number or phase operator,the following parameters are defined

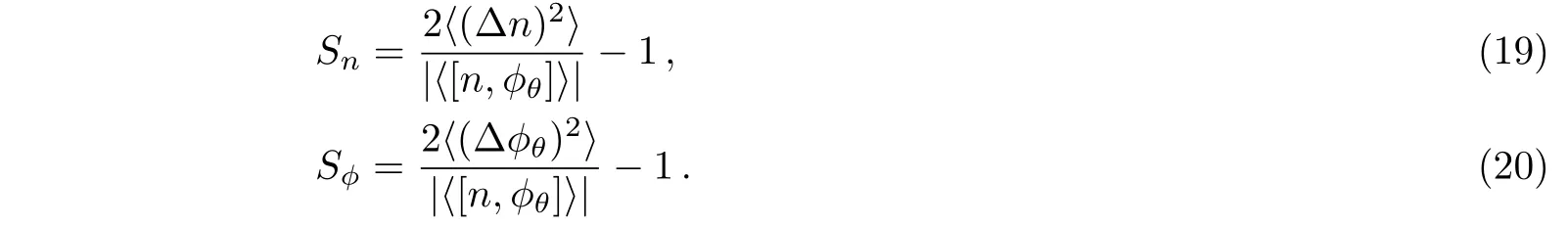
If Sn<0(Sϕ<0),the corresponding state is the number(phase)squeezed.

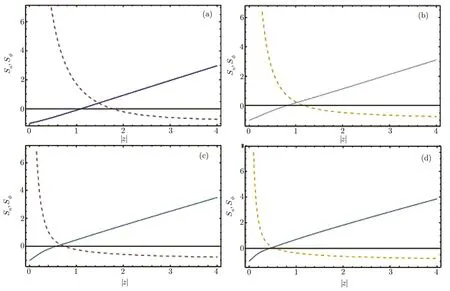
Fig.3 Plot of the number and phase squeezing associated with the photon-added coherent states for anharmonic oscillators versus|z|withµ=1 for(a)m=0,(b)m=1,(c)m=3,and(d)m=5.

The number and phase squeezing parameters associated with these states are shown in Fig.3 for different values of m.It can be seen from the figure as|z|increases,squeezing parameters Sn(solid curve)and Sϕ(dotted curve)are increased and decreased,respectively and so they have opposite behavior.For small values of|z|,squeezing in number operator and for large values of|z|,squeezing in phase operator is observed.Also,there is a region with no squeezing.For example in Fig.3(b)with m=1,as|z|becomes smaller than 0.802,Snis negative that shows the squeezing is occurred in numbers operator.Also,for|z|&1.177,Sϕ<0,and Sn>0 that indicates the squeezing is happened in phase operator.The squeezing is not occurred in 0.802.|z|.1.177.As m increases,the region with no squeezing is decreased.

6 Number-phase Entropic Uncertainty Relations

The Shannon entropies(SAand SB)of two conjugate operators A and B,with eigenvalue equations A|an⟩=an|an⟩and B|bn⟩=bn|an⟩,are limited by the entropy uncertainty relation SA+SB≥ln(s+1).Here A and B are defined on the(s+1)-dimensional space.This uncertainty relation which has been suggested by Kraus[20]and then proven by Massen and Uffink,[21]depends on dimension of the state space.Vaccaro et al.defined new quantities RAand RBas follows

where δaand δbrepresent the differences between the eigenvalues corresponding to operators A and B,respectively.Using RAand RAinstead of SAand SBa new form of entropic uncertainty relation can be obtained as RA+RB≥ ln(2π).[22]The general conjugate operators A and B can be replaced with ϕθand n operators by selecting δa=2π/s+1 and δb=1.So,the entropic uncertainty relation for phase and number operators is as follows[23]

Now,the number-phase entropic uncertainty relation associated with photon-added coherent states for anharmonic oscillators in nonlinear Kerr medium is considerable.In the in finite s limit,the Rϕis given by[22−23]

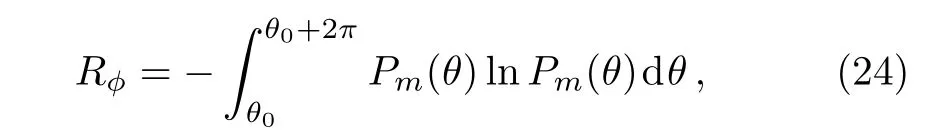
where Pm(θ)is the phase distribution function obtained in Eq.(15).Also,the photon number entropy for introduced states is defined as

Finally,by using(6)in(25)the following expression for photon number entropy of photon-added coherent states associated with anharmonic oscillators can be obtained

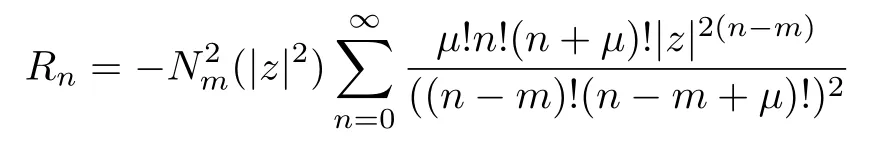
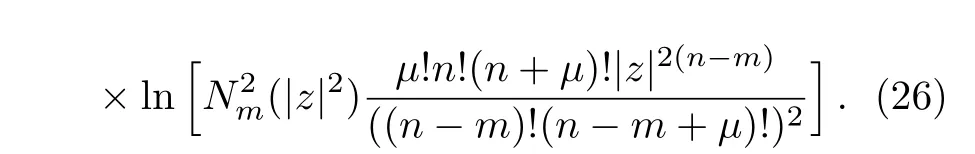
In Fig.4,Rϕ,Rnand their sum have been depicted versus|z|for photon-added coherent states corresponding to anharmonic oscillators with m=1.The figure shows that Rnincreases while Rϕdecreases with increasing z.It can be observed that their sum according to Eq.(23)has a lower bound ln(2π).Also,because of the vacuum is an eigenstate of the number operator,the sum Rn+Rϕis exactly ln(2π)at z=0.

Fig.4 Plots of Rn(solid curve),Rϕ(dashed curve)and their sum(dot-dashed curve)versus|z|associate with the photon-added coherent states for anharmonic oscillators in a Kerr medium withµ=1 and m=1.

7 Summary and Conclusion

The phase and number properties of physical systems are very important. In this work,the number-phase Wigner function,phase distribution function,numberphase squeezing and number-phase entropic uncertainty relation of the photon-added coherent states for anharmonic oscillators are studied using Pegg-Barnett formalism.The number-phase Wigner function corresponding to these generalized coherent states is negative in some regions.The results show also that these states represent number or phase squeezing for different ranges of|z|.Therefore,these states are nonclassical states.The photon-added coherent state for anharmonic oscillators can be considered as an intermediate state between the coherent states for anharmonic oscillators and the Fock states.Construction of a photon-added coherent state for anharmonic oscillators by adding photon to the coherent state for anharmonic oscillators is a proper way to have a quantum state with more nonclassicality.The curves of Pegg-Barnett phase distribution function show that this distribution function has only a single peak in θ=0 and as m increases,the peak is more localized with respect to θ.Finally,it is found that the number-phase entropic uncertainty relation associated with the photon-added coherent states for anharmonic oscillators has a lower bound ln(2π)for all values of photon added number m.

[1]E.Schrodinger,Naturwissenschaften 14(1926)664.

[2]S.Iqbal,Phys.Lett.A 356(2006)231.

[3]R.W.Robinett,J.Math.Phys.41(2000)1801.

[4]P.Roy,Opt.Commun.221(2003)145.

[5]M.A.Al-Rajhi and S.Abdel-Khalek,Int.J.Theor.Phys.54(2015)1470.

[6]G.Agarwal and K.Tara,Phys.Rev.A 43(1991)492.

[7]S.Sivakumar,J.Phys.A:Math.Gen.32(1999)3441.

[8]M.Naderi,J.Phys.A:Math.Gen.37(2004)3225.

[9]A.Zavatta,S.Viciani,and M.Bellini,Phys.Rev.A 72(2005)023820.

[10]D.Kalamidas,C.C.Gerry,and A.Benmoussa,Phys.Lett.A 372(2008)1937.

[11]K.Berrada,J.Math.Phys.56(2015)072104.

[12]H.C.Yuan,X.X.Xu,and H.Y.Fan,Chin.Phys.B 19(2010)104205.

[13]D.Popov,J.Phys.A:Math.Gen.35(2002)7205.

[14]M.N.Hounkonnou and E.B.Ngompe Nkouankam,J.Phys.A:Math.Theor.42(2009)025206.

[15]R.Rom´an-Ancheyta,C.Gonz´alez Guti´errez,and J.R´ecamier,J.Opt.Soc.Am.B 31(2014)38.

[16]M.A.Al-Rajhi,Modern.Phys.Lett.B 29(2015)1550035.

[17]J.Vaccaro,Phys.Rev.A 52(1995)3474.

[18]J.A.Vaccaro,Opt.Commun.113(1995)421.

[19]D.Pegg and S.Barnett,Phys.Rev.A 39(1989)1665.

[20]K.Kraus,Phys.Rev.D 35(1987)3070.

[21]H.Maassen and J.B.Uffink,Phys.Rev.Lett.60(1988)1103.

[22]A.R.Gonzalez,J.A.Vaccaro,and S.M.Barnett,Phys.Lett.A 205(1995)247.

[23]G.R.Honarasa,M.K.Tavassoly,and M.Hatami,Phys.Lett.A 373(2009)3931.